Demand Forecasting and Production Planning at M&L Manufacturing
VerifiedAdded on 2023/06/04
|9
|1635
|112
Report
AI Summary
This report addresses the challenge of production forecasting at M&L Manufacturing, where intuition-based methods have led to uneven demand and inventory issues. It highlights the superiority of formalized forecasting techniques for efficient raw material ordering, inventory management, cost reduction, and profit maximization. The report analyzes data for two products, applying regression analysis to Product 1 after addressing an outlier, and employing a naive method for Product 2 due to its complex data pattern. The analysis provides specific production forecasts for the upcoming weeks, aiming to improve production planning and reduce tensions with retail outlets. Desklib provides students access to solved assignments and past papers.

Running head: FORECASTING OF TWO PRODUCTS
Forecasting of Two Products
Name of the Student
Name of the University
Author Note
Forecasting of Two Products
Name of the Student
Name of the University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1FORECASTING OF TWO PRODUCTS
Answer to Question 1
The term forecasting refers to the technique of estimation of the future values of a
product or an industry by looking or analyzing the historical data (Box et.al., 2015). These
historical data are considered as the inputs and based on these inputs an appropriate method
of forecasting is chosen. A formalized method of forecasting is far superior as compared to a
less formalized approach. In the case of a less formalized method of forecasting, the process
of forecasting is carried out based on the intuition of the individuals (Moser & Kalton, 2017).
Suppose for example that the production of M&L manufacturing. The company does not
utilize any formalized forecasting technique. The whole decision of forecasting is solely
based on the intuition of the manager. The manager decides which products to produce based
on the demand and the quantity of inventories. Products that have the minimum amount of
inventories receive the highest priority. As a result of this intuition based forecasting the
company has experienced uneven demand along with overstocking of few items and literally
zero stockings for few items.
A more formalized method of forecasting tends to improve the process of
manufacturing by ordering the correct amount of the raw materials (Hyndman &
Athanasopoulos, 2018). This process also helps to maintain a proper level of inventory
accumulation. The formalized process of forecasting also helps to minimize the costs of
production and increase the level of profits that are acquiring to the firm. This formalized
process of forecasting also helps a firm to decide whether the industry should add to the
inventories or slow down production due to changes that are occurring to the industry. Thus,
a more formalized method of forecasting will help the industry to make better long run plans
and also to develop a better prediction for the future which will increase the profits as well as
minimize the costs of the industry.
Answer to Question 1
The term forecasting refers to the technique of estimation of the future values of a
product or an industry by looking or analyzing the historical data (Box et.al., 2015). These
historical data are considered as the inputs and based on these inputs an appropriate method
of forecasting is chosen. A formalized method of forecasting is far superior as compared to a
less formalized approach. In the case of a less formalized method of forecasting, the process
of forecasting is carried out based on the intuition of the individuals (Moser & Kalton, 2017).
Suppose for example that the production of M&L manufacturing. The company does not
utilize any formalized forecasting technique. The whole decision of forecasting is solely
based on the intuition of the manager. The manager decides which products to produce based
on the demand and the quantity of inventories. Products that have the minimum amount of
inventories receive the highest priority. As a result of this intuition based forecasting the
company has experienced uneven demand along with overstocking of few items and literally
zero stockings for few items.
A more formalized method of forecasting tends to improve the process of
manufacturing by ordering the correct amount of the raw materials (Hyndman &
Athanasopoulos, 2018). This process also helps to maintain a proper level of inventory
accumulation. The formalized process of forecasting also helps to minimize the costs of
production and increase the level of profits that are acquiring to the firm. This formalized
process of forecasting also helps a firm to decide whether the industry should add to the
inventories or slow down production due to changes that are occurring to the industry. Thus,
a more formalized method of forecasting will help the industry to make better long run plans
and also to develop a better prediction for the future which will increase the profits as well as
minimize the costs of the industry.

2FORECASTING OF TWO PRODUCTS
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3FORECASTING OF TWO PRODUCTS
Answer to Question 2
Looking into the data that is provided for the first product that is of the product 1 it
can be seen that the values follow somewhat a linear trend. From the first week it can be
observed that the production of the first commodity is rising. However in the seventh week
the value is abnormally high at 90. This value might be considered as an outlier (Aggarwal,
2015). There are various methods to deal with an outlier. Here, the outlier cannot be omitted
as the data set is too small. Thus, the outlier in this question is replaced by taking the average
of the previous 6th and the 8th week (Johansen & Nielsen, 2016). The average of the previous
week and the preceding week is used in the place of the outlier value of the 7th week.
Therefore the value of 90 is replaced (67 + 76)/2 which equals 71.5.
After replacing the value of the outlier regression has been used as a tool to forecast
the preceding four weeks production of the industry (Kenney, 2013). The process of this
regression is performed using MS excel (Evans, 2013). From the following data it can be
seen that there are two variables namely production and week. The production is the
dependent variable and time is the independent variable. A linear relationship between the
two variables is established by running the regression. After running the regression the
following results were observed,
Coefficients Standard
Error
t Stat P-value
Intercept 46.6593 0.422232877 110.5062 2.02E-19
Week 3.497802198 0.049588737 70.53622 4.38151E-17
Table: 3: Regression Statistics
Source: Author’s own creation in MS Excel
Answer to Question 2
Looking into the data that is provided for the first product that is of the product 1 it
can be seen that the values follow somewhat a linear trend. From the first week it can be
observed that the production of the first commodity is rising. However in the seventh week
the value is abnormally high at 90. This value might be considered as an outlier (Aggarwal,
2015). There are various methods to deal with an outlier. Here, the outlier cannot be omitted
as the data set is too small. Thus, the outlier in this question is replaced by taking the average
of the previous 6th and the 8th week (Johansen & Nielsen, 2016). The average of the previous
week and the preceding week is used in the place of the outlier value of the 7th week.
Therefore the value of 90 is replaced (67 + 76)/2 which equals 71.5.
After replacing the value of the outlier regression has been used as a tool to forecast
the preceding four weeks production of the industry (Kenney, 2013). The process of this
regression is performed using MS excel (Evans, 2013). From the following data it can be
seen that there are two variables namely production and week. The production is the
dependent variable and time is the independent variable. A linear relationship between the
two variables is established by running the regression. After running the regression the
following results were observed,
Coefficients Standard
Error
t Stat P-value
Intercept 46.6593 0.422232877 110.5062 2.02E-19
Week 3.497802198 0.049588737 70.53622 4.38151E-17
Table: 3: Regression Statistics
Source: Author’s own creation in MS Excel
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4FORECASTING OF TWO PRODUCTS
The coefficient of the intercept term is 46.65 and the value of the slope coefficient b is
3.49. Thus, the estimated equation of the first product can be written as,
Y t =46.65+3.49 t
Where, Y t is the production of the company in period t. The significance of the
estimated values needs to be checked. The p-values of each of the terms helps to judge this
matter. For both the terms the value is lower than 0.05 which means that the values are
significant at 5 percent level of significance (Greenland et.al., 2016). Moreover, the
credibility of this equation also depends on the value of the adjusted R square.
Regression Statistics
Multiple R 0.998796234
R Square 0.997593917
Adjusted R Square 0.99739341
Standard Error 0.747952027
Observations 14
Table: 2: Regression Statistics
Source: Author’s own creation in MS Excel
From the analysis it can be seen that the model explains 99 percent variation in
production with respect to week. Thus, the method is appropriate (Darlington & Hayes,
2016). This simple equation helps to determine the level of production for the next four
weeks.
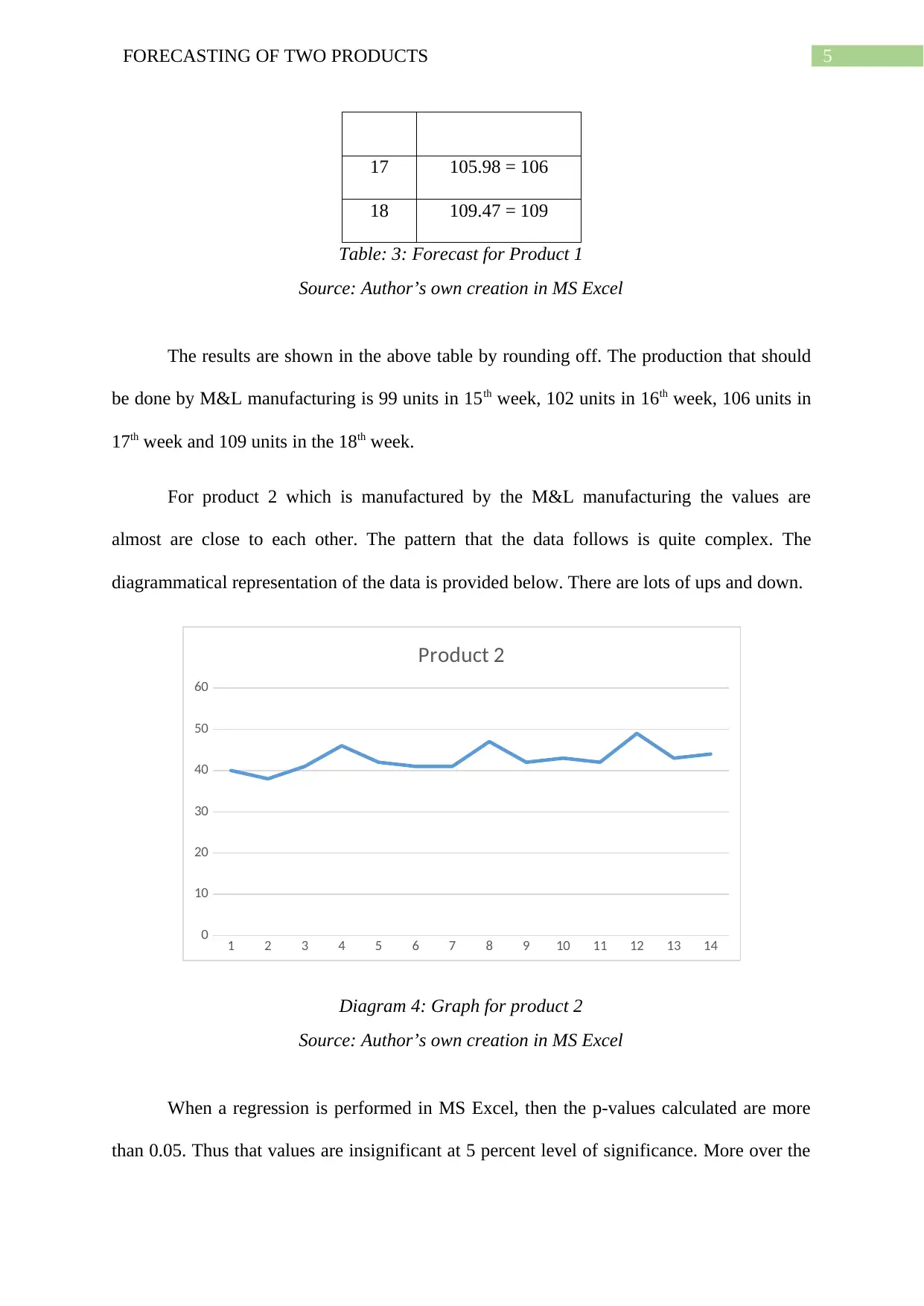
Week Production
15 99
16 102.49 = 102
The coefficient of the intercept term is 46.65 and the value of the slope coefficient b is
3.49. Thus, the estimated equation of the first product can be written as,
Y t =46.65+3.49 t
Where, Y t is the production of the company in period t. The significance of the
estimated values needs to be checked. The p-values of each of the terms helps to judge this
matter. For both the terms the value is lower than 0.05 which means that the values are
significant at 5 percent level of significance (Greenland et.al., 2016). Moreover, the
credibility of this equation also depends on the value of the adjusted R square.
Regression Statistics
Multiple R 0.998796234
R Square 0.997593917
Adjusted R Square 0.99739341
Standard Error 0.747952027
Observations 14
Table: 2: Regression Statistics
Source: Author’s own creation in MS Excel
From the analysis it can be seen that the model explains 99 percent variation in
production with respect to week. Thus, the method is appropriate (Darlington & Hayes,
2016). This simple equation helps to determine the level of production for the next four
weeks.
Week Production
15 99
16 102.49 = 102
5FORECASTING OF TWO PRODUCTS
17 105.98 = 106
18 109.47 = 109
Table: 3: Forecast for Product 1
Source: Author’s own creation in MS Excel
The results are shown in the above table by rounding off. The production that should
be done by M&L manufacturing is 99 units in 15th week, 102 units in 16th week, 106 units in
17th week and 109 units in the 18th week.
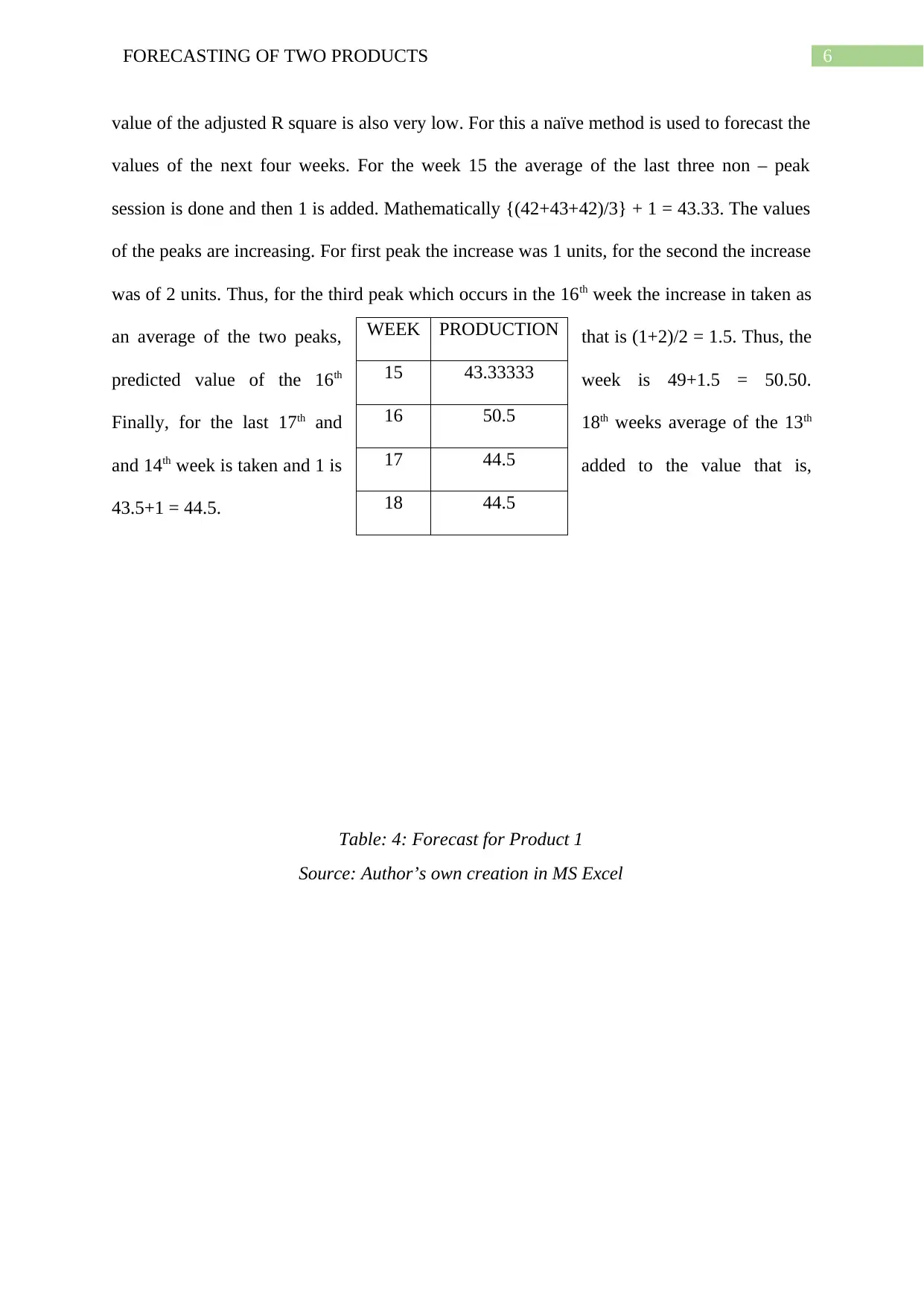
For product 2 which is manufactured by the M&L manufacturing the values are
almost are close to each other. The pattern that the data follows is quite complex. The
diagrammatical representation of the data is provided below. There are lots of ups and down.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
10
20
30
40
50
60
Product 2
Diagram 4: Graph for product 2
Source: Author’s own creation in MS Excel
When a regression is performed in MS Excel, then the p-values calculated are more
than 0.05. Thus that values are insignificant at 5 percent level of significance. More over the
17 105.98 = 106
18 109.47 = 109
Table: 3: Forecast for Product 1
Source: Author’s own creation in MS Excel
The results are shown in the above table by rounding off. The production that should
be done by M&L manufacturing is 99 units in 15th week, 102 units in 16th week, 106 units in
17th week and 109 units in the 18th week.
For product 2 which is manufactured by the M&L manufacturing the values are
almost are close to each other. The pattern that the data follows is quite complex. The
diagrammatical representation of the data is provided below. There are lots of ups and down.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
10
20
30
40
50
60
Product 2
Diagram 4: Graph for product 2
Source: Author’s own creation in MS Excel
When a regression is performed in MS Excel, then the p-values calculated are more
than 0.05. Thus that values are insignificant at 5 percent level of significance. More over the
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6FORECASTING OF TWO PRODUCTS
value of the adjusted R square is also very low. For this a naïve method is used to forecast the
values of the next four weeks. For the week 15 the average of the last three non – peak
session is done and then 1 is added. Mathematically {(42+43+42)/3} + 1 = 43.33. The values
of the peaks are increasing. For first peak the increase was 1 units, for the second the increase
was of 2 units. Thus, for the third peak which occurs in the 16th week the increase in taken as
an average of the two peaks, that is (1+2)/2 = 1.5. Thus, the
predicted value of the 16th week is 49+1.5 = 50.50.
Finally, for the last 17th and 18th weeks average of the 13th
and 14th week is taken and 1 is added to the value that is,
43.5+1 = 44.5.
Table: 4: Forecast for Product 1
Source: Author’s own creation in MS Excel
WEEK PRODUCTION
15 43.33333
16 50.5
17 44.5
18 44.5
value of the adjusted R square is also very low. For this a naïve method is used to forecast the
values of the next four weeks. For the week 15 the average of the last three non – peak
session is done and then 1 is added. Mathematically {(42+43+42)/3} + 1 = 43.33. The values
of the peaks are increasing. For first peak the increase was 1 units, for the second the increase
was of 2 units. Thus, for the third peak which occurs in the 16th week the increase in taken as
an average of the two peaks, that is (1+2)/2 = 1.5. Thus, the
predicted value of the 16th week is 49+1.5 = 50.50.
Finally, for the last 17th and 18th weeks average of the 13th
and 14th week is taken and 1 is added to the value that is,
43.5+1 = 44.5.
Table: 4: Forecast for Product 1
Source: Author’s own creation in MS Excel
WEEK PRODUCTION
15 43.33333
16 50.5
17 44.5
18 44.5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

7FORECASTING OF TWO PRODUCTS
References
Aggarwal, C. C. (2015). Outlier analysis. In Data mining (pp. 237-263). Springer, Cham.
Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis:
forecasting and control. John Wiley & Sons.
Darlington, R. B., & Hayes, A. F. (2016). Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Evans, J. R. (2013). Business analytics: Methods, models, and decisions (Vol. 3). Upper
Saddle River, NJ: Pearson.
Greenland, S., Senn, S. J., Rothman, K. J., Carlin, J. B., Poole, C., Goodman, S. N., &
Altman, D. G. (2016). Statistical tests, P values, confidence intervals, and power: a
guide to misinterpretations. European journal of epidemiology, 31(4), 337-350.
Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
Johansen, S., & Nielsen, B. (2016). Asymptotic theory of outlier detection algorithms for
linear time series regression models. Scandinavian Journal of Statistics, 43(2), 321-
348.
Kenney, J. F. (2013). Mathematics of statistics. D. Van Nostrand Company Inc; Toronto;
Princeton; New Jersey; London; New York,; Affiliated East-West Press Pvt-Ltd; New
Delhi.
Moser, C. A., & Kalton, G. (2017). Survey methods in social investigation. Routledge.
References
Aggarwal, C. C. (2015). Outlier analysis. In Data mining (pp. 237-263). Springer, Cham.
Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis:
forecasting and control. John Wiley & Sons.
Darlington, R. B., & Hayes, A. F. (2016). Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Evans, J. R. (2013). Business analytics: Methods, models, and decisions (Vol. 3). Upper
Saddle River, NJ: Pearson.
Greenland, S., Senn, S. J., Rothman, K. J., Carlin, J. B., Poole, C., Goodman, S. N., &
Altman, D. G. (2016). Statistical tests, P values, confidence intervals, and power: a
guide to misinterpretations. European journal of epidemiology, 31(4), 337-350.
Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
Johansen, S., & Nielsen, B. (2016). Asymptotic theory of outlier detection algorithms for
linear time series regression models. Scandinavian Journal of Statistics, 43(2), 321-
348.
Kenney, J. F. (2013). Mathematics of statistics. D. Van Nostrand Company Inc; Toronto;
Princeton; New Jersey; London; New York,; Affiliated East-West Press Pvt-Ltd; New
Delhi.
Moser, C. A., & Kalton, G. (2017). Survey methods in social investigation. Routledge.

8FORECASTING OF TWO PRODUCTS
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




