Frequency distribution of Melbourne 20 18 18 16 14 12 to 1577 1577 to 1859 1 1 1859 to 2140 2140 to 2422 2422 to 2703 Number of passengers at train station (Melbourne) 20 18 18 16 14 12

[Date]
STATISTICS
SML
[company name]

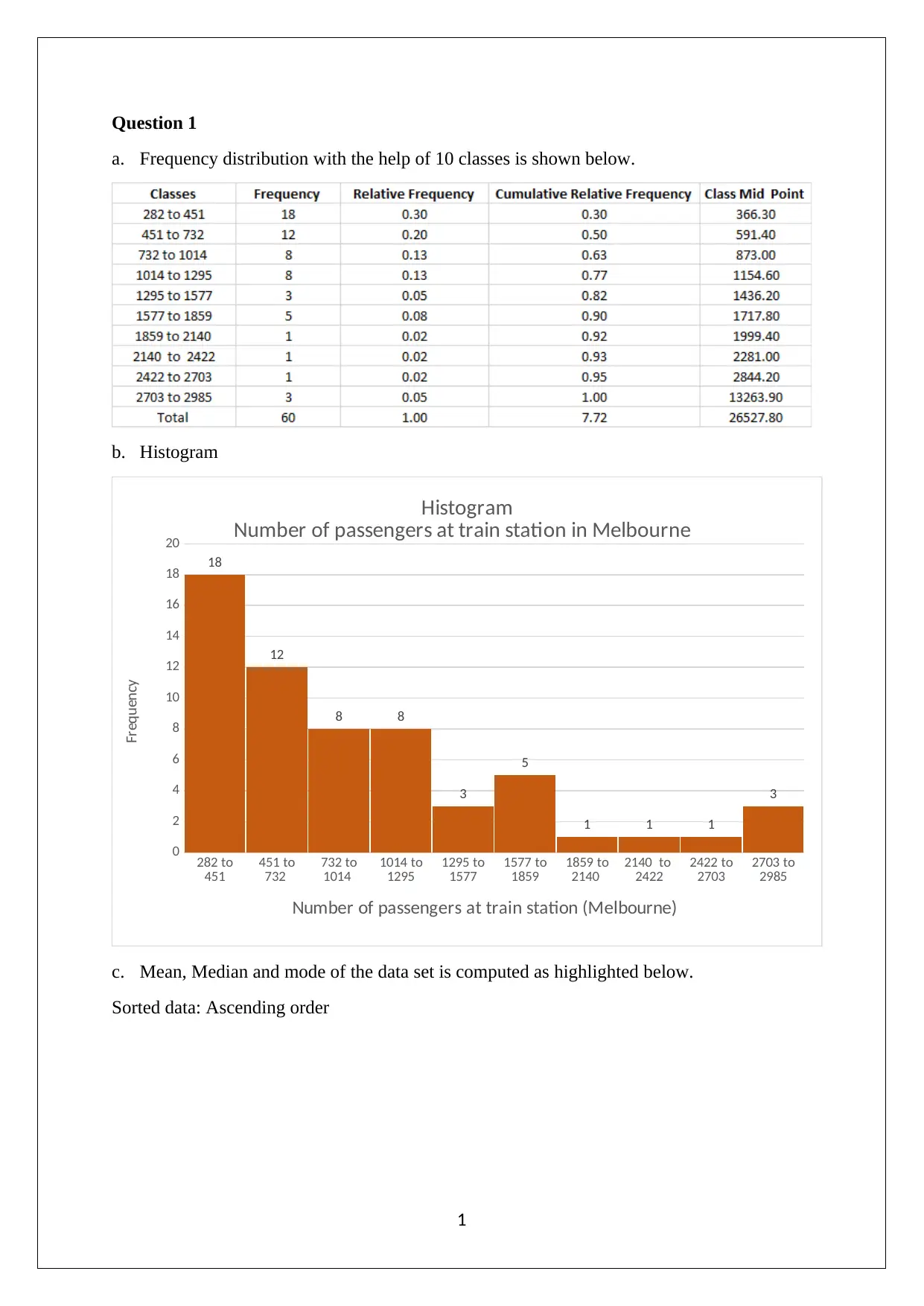
Question 1
a. Frequency distribution with the help of 10 classes is shown below.
b. Histogram
282 to
451 451 to
732 732 to
1014 1014 to
1295 1295 to
1577 1577 to
1859 1859 to
2140 2140 to
2422 2422 to
2703 2703 to
2985
0
2
4
6
8
10
12
14
16
18
20
18
12
8 8
3
5
1 1 1
3
Histogram
Number of passengers at train station in Melbourne
Number of passengers at train station (Melbourne)
Frequency
c. Mean, Median and mode of the data set is computed as highlighted below.
Sorted data: Ascending order
1

2

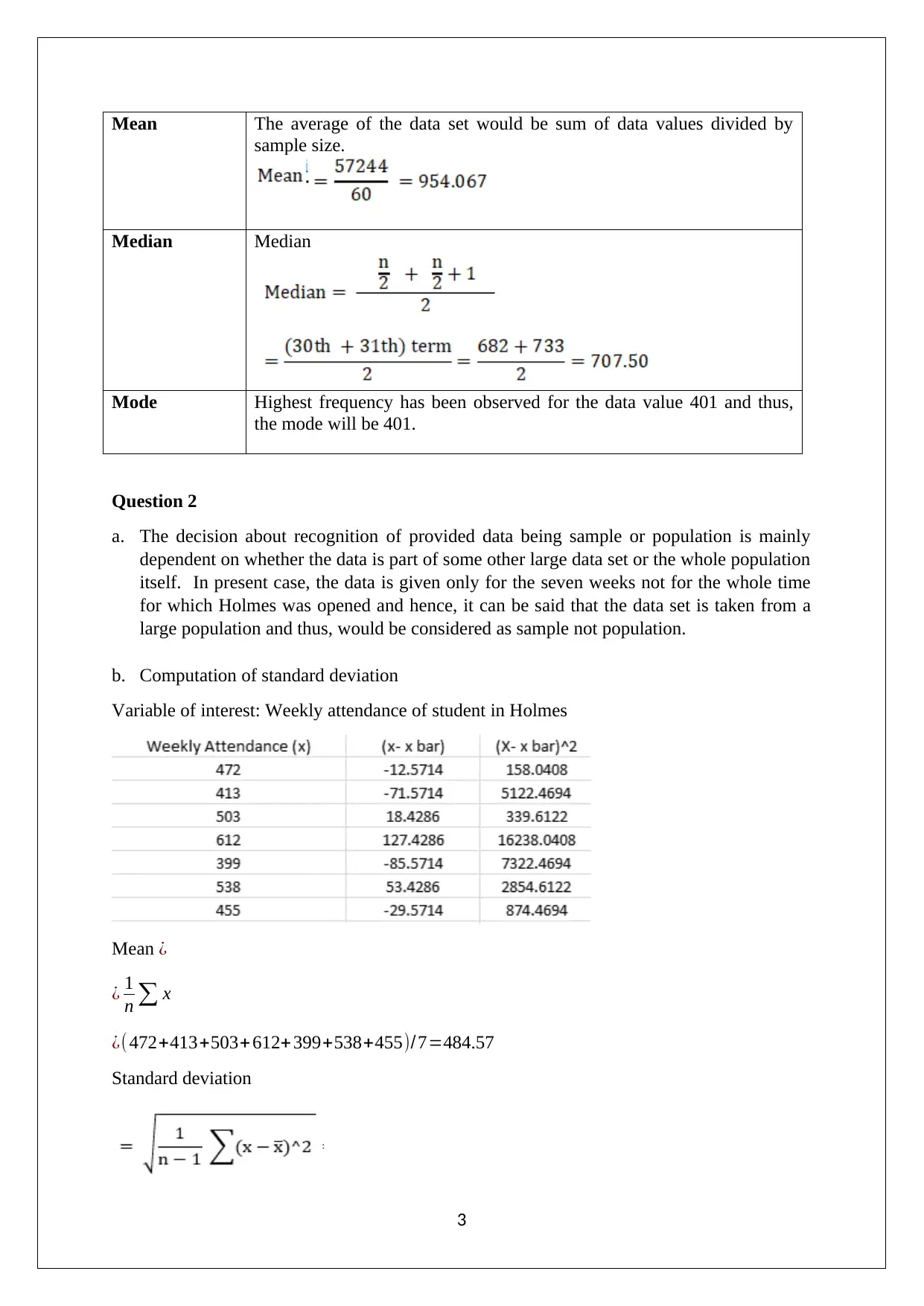
Mean The average of the data set would be sum of data values divided by
sample size.
Median Median
Mode Highest frequency has been observed for the data value 401 and thus,
the mode will be 401.
Question 2
a. The decision about recognition of provided data being sample or population is mainly
dependent on whether the data is part of some other large data set or the whole population
itself. In present case, the data is given only for the seven weeks not for the whole time
for which Holmes was opened and hence, it can be said that the data set is taken from a
large population and thus, would be considered as sample not population.
b. Computation of standard deviation
Variable of interest: Weekly attendance of student in Holmes
Mean ¿
¿ 1
n ∑ x
¿(472+413+503+ 612+ 399+538+455)/7=484.57
Standard deviation
3

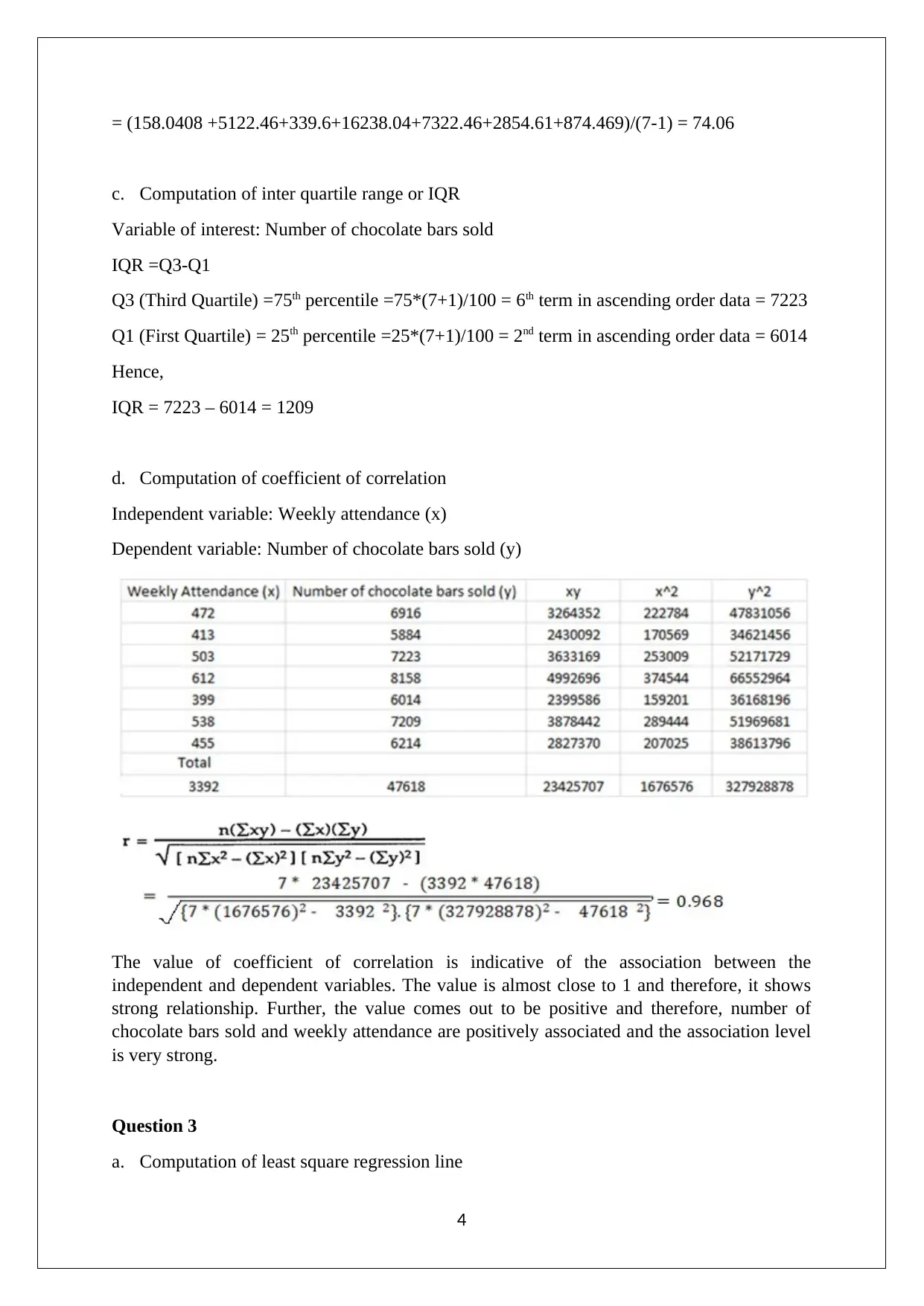
= (158.0408 +5122.46+339.6+16238.04+7322.46+2854.61+874.469)/(7-1) = 74.06
c. Computation of inter quartile range or IQR
Variable of interest: Number of chocolate bars sold
IQR =Q3-Q1
Q3 (Third Quartile) =75th percentile =75*(7+1)/100 = 6th term in ascending order data = 7223
Q1 (First Quartile) = 25th percentile =25*(7+1)/100 = 2nd term in ascending order data = 6014
Hence,
IQR = 7223 – 6014 = 1209
d. Computation of coefficient of correlation
Independent variable: Weekly attendance (x)
Dependent variable: Number of chocolate bars sold (y)
The value of coefficient of correlation is indicative of the association between the
independent and dependent variables. The value is almost close to 1 and therefore, it shows
strong relationship. Further, the value comes out to be positive and therefore, number of
chocolate bars sold and weekly attendance are positively associated and the association level
is very strong.
Question 3
a. Computation of least square regression line
4

A least square regression line is in the form of y=mx+c
Where, m=slope , c=Intercept
For slope (m)
For intercept (c)
Hence,
y=1628.689+(10.677 x)
Number of chocolate bars sold=1628.689+(Weekly attendance∗10.677)
 The value of the weekly attendance of student (variable) will be zero when Holmes is
closed for students. In this scenario, the number of chocolate bars sold is calculated based
on the least square regression line.
Put weekly attendance (x) = 0 in the equation and then the number of chocolate bars sold =
1628.689 or 1629
 Let there be extra 10 students and hence, the independent variable will be 10.67(x + 10).
The number of chocolate bars sold = 1628.689 + 10.67 (x+10) = 1628.689 + 10.67 x + 1067
= 2695.689+10.67x
b. Computation of coefficient of determination
R (coefficient of correlation) = 0.968
R2 (coefficient of determination) = (0.968)2 = 0.937
The coefficient of determination (0.937) indicates that 93.70% of changes in number of
chocolate bars sold would be explained by change in the weekly attendance of the students
5

enrolled at Holmes. The percentage is significantly high and therefore, it can be said that the
regression model is considered to be a good fit.
Question 4
Training and recruitment data are shown below.
a. P ( Holmes∨Grassroots training )
Favourable case = 35 +92 +12 = 139
Total cases = 35 +54 +92 +12 = 193
P=Favourable case/Total cases=139/193
P=0.720
b. P ( External∧Scientific training )
Favourable case = 54
Total cases = 35 +54 +92 +12 = 193
P=Favourable case/Total cases=54/193
P=0.280
c. P ( Scientific training∧¿ Holmes )
Favourable case = 35
Total cases = 35 +92 = 193
P=Favourable case/Total cases=35/127
P=0.276
d. Training and recruitment are independent or dependent events.
A = Training
B = Recruitment
A & B will be independent when P (A and B) = P(A). P (B)
P (A), P (B) and P (A and B) =?
6

Computation P (A)
Favourable case = 54+12 = 66
Total cases = 35 +54+92+12 = 193
P( A)=Favourable case/Total cases=66/193=0.3419
Computation P (B)
Favourable case = 35+54 = 89
Total cases = 35 +54+92+12 = 193
P(B)=Favourable case/Total cases=89 /193=0.4611
Now,
P ( A∧B )=0.2570
P ( A ) . P ( B )=0.3419∗0.4611=0.1576
It is apparent that the necessary term required for A and B being independent events is not
fulfilled and therefore, Training and Recruitment is not termed as independent events.
Question 5
a. There are 3 products X, Y and Z and 4 consumer segments A, B, C and D.
Segment A – 55% of consumers interest in functionality of the products
Segment B – 30% of consumers is highly price sensitive
Segment C- 10% of consumers is interest in appearance and styling of the products
Segment D- 5% of consumers are fashion conscious and buy products which are endorsed by
celebrities
The given probability information is listed below.
Probability that person from segment A would prefer X product = 20%
Probability that person from segment B would prefer X product = 35%
Probability that person from segment C would prefer X product = 60%
Probability that person from segment D would prefer X product = 90%
Probability that a person coming from segment A would prefer product X over product Y and
product Z =?
7

Bayes’ Rule
P ( Segment A| Product X ¿
¿ 55 %∗20 %
{ ( 55 %∗20 % ) + ( 35 %∗30 % ) + ( 60 %∗10 % ) + ( 90 %∗5 % ) }
¿ 0.3537
b. Probability that a randomly selected consumer’s first preference would be product X
P ( X ) = { ( 55 %∗20 % ) + ( 35 %∗30 % ) + ( 60 %∗10 % ) + ( 90 %∗5 % ) }
¿ 0.32
Question 6
a. Count of people who enter in the store n = 8
Probability that only 2 or less of those 8 would buy anything from the store =?
Probability that customer would buy something from store p = 1 / 10 = 0.10
Formula for Binomial distribution would be used to find the requisite probability.
Probability that only 2 or less of those 8 would buy anything from the store is 0.9619.
b. Number of customers entering every 2 minutes = 9
Formula for Poisson distribution would be used to find the requisite probability.
Probability that number of customers entering every 2 minutes is 9 would be 0.124.
Question 7
Mean of sale price = $1.1 million or $1,100,000
8

Standard deviation of sale price = $385,000
a. Probability that the respective apartment would be sold for a price more than $2 million
or $2000000
Formula for Normal distribution would be used to find the requisite probability.
b. Probability that the respective apartment would be sold for a price between $1 million and
$1.1 million
Question 8
a. It is given that Surfers Paradise is a mix of the cheap older and more expensive new
apartments and the distribution is not normal. Here, we will use z distribution to test the
findings of the assistance because as per central limit theorem, the z distribution would be
used when the sample size is higher than 30 as when large sample size is taken into
account then the distribution would assume to be normal. Here, the sample size is higher
than 30 which indicates that z distribution would be used.
b. Only 11 investors are agreed to make the investment out of 45 investors.
The requisite proportion = 11 /45 =0.24
Standard error = sqrt (p(1-p)/n) = sqrt(0.24 (1-0.24)/45) = 0.064
Probability that the above proportion will be more than 0.30.
P ( p >0.30 )=P ( z> 0.30−0.240
0.064 )=0.192
9

10