Mechanical Engineering Statics Problems: Assignment Solution
VerifiedAdded on 2022/08/12
|9
|700
|24
Homework Assignment
AI Summary
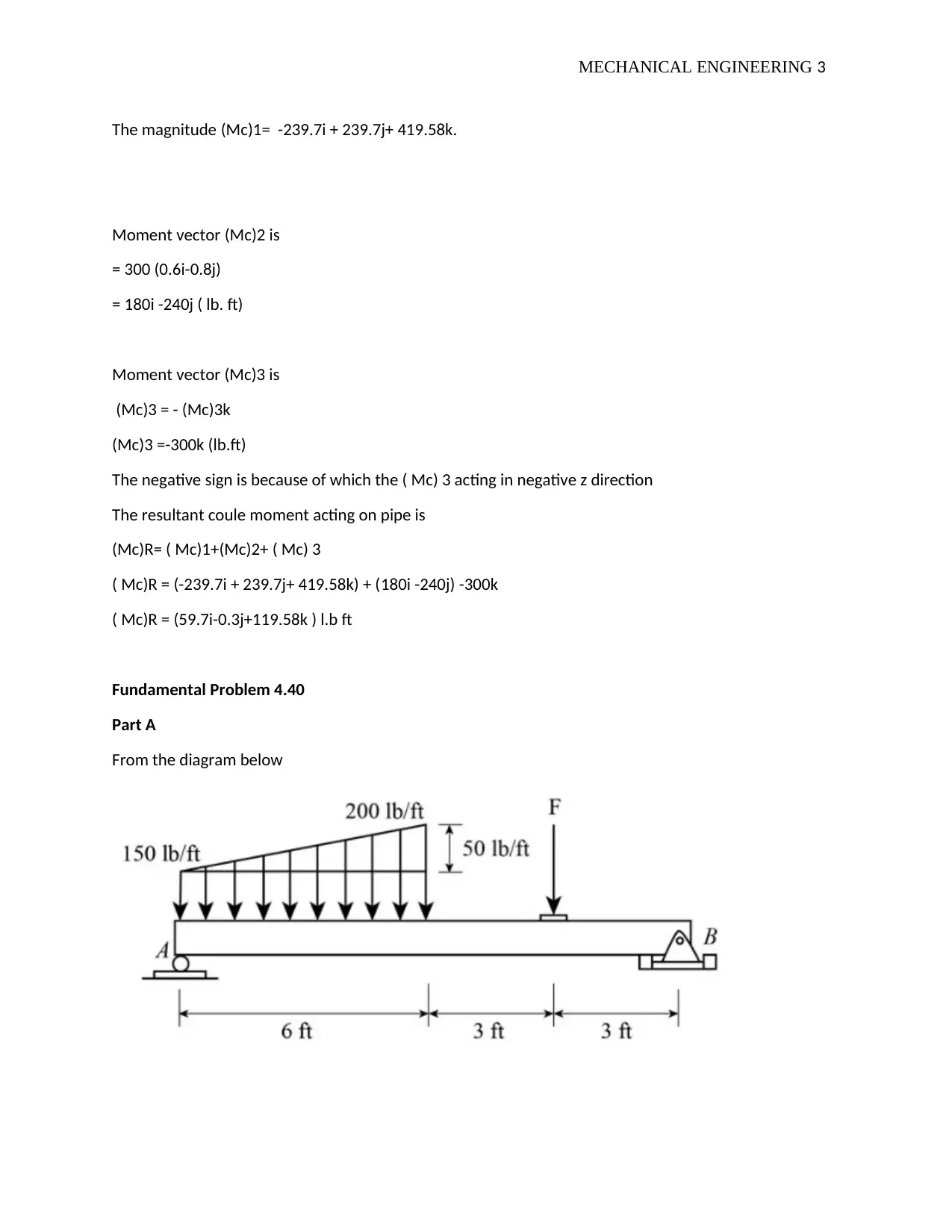
This document presents a comprehensive solution to a mechanical engineering assignment, focusing on statics problems. It meticulously solves various fundamental problems, including calculations of moment vectors, resultant forces, and the application of Varignon's theorem. The solutions involve detailed step-by-step calculations, vector analysis, and equilibrium conditions, providing a clear understanding of the underlying principles. Furthermore, the document addresses problems related to force application points and the determination of resultant force locations. The assignment covers a range of topics within statics, making it a valuable resource for students studying mechanical engineering and related fields. References to relevant research papers are also included, enhancing the academic rigor of the solutions.
1 out of 9














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)