Game Theory and Social Dilemma: A Case Study of Monopolistic Competition Market

This report discusses the application of game theory and payoff matrix in solving the social dilemma of pricing decision in monopolistic competition market. It covers dominant strategy, Nash equilibrium, and self-interested behavior. The report also compares the predicted outcome with socially desired outcome.

INDIVIDUAL WRITTEN

Table of Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY..................................................................................................................................3
Explanation of real – world social dilemma................................................................................3
Two Game matrices based on social dilemma............................................................................3
Explanation of payoffs assigned to each strategy and outcome their relevance with the social
dilemma.......................................................................................................................................5
Rules of the game........................................................................................................................6
Concept of dominant strategy, Nash equilibrium and self – interested behavior........................6
Description of Nash equilibrium, explanation of predicted outcome and its comparison with
socially desired outcome..............................................................................................................8
Overcoming the social dilemma by relating it to the payoff matrix............................................9
Success of proposed solution in motivating players towards socially optimal outcome.............9
Effect of non – cooperative interactions on social dilemma and its potentiality in overcoming
the stated social dilemma...........................................................................................................10
CONCLUSION..............................................................................................................................10
REFERENCES..............................................................................................................................11
Books and Journals....................................................................................................................11

INTRODUCTION
Game theory is basically a mathematical model of strategic interaction which involve the
study of how and why people make decisions. It means game theory is one of the tool of
decision-making. In the present project, the selected social dilemma is pricing decision of the
two firm in the monopolistic competition market. The project will provide the solutions to social
dilemma chosen using game theory and payoff matrix (Azis, 2022). Further, the project will
cover the dominant strategy, Nash equilibrium and self-interested behavior. Lastly, the project
will cover the effect of non-cooperative interaction on social dilemma and its potential to
overcome the social dilemma stated in present project.
MAIN BODY
Explanation of real – world social dilemma
For this project report, one of the most popular social dilemma has been chosen
pertaining to the monopolistic market which involves taking pricing decision or chosen the right
pricing strategy (Bertoletti and Etro, 2022). Accordingly, in the given scenario, there are two
firms competing with each other in a monopolistic market situation where firms generally aim to
increase their revenue by lowering their prices. It is one of the feature of monopolistic market
where firms at the first hand determines the level of output they want to generate and
accordingly, fixes the prices of their products and services to attain the desired level of revenue
by selling their produced output. The two firms are Firm A and Firm B and both of these firms
are having two strategies that is, either to raise or lower the prices of their produce. Firms are
independent of each other, however there must be a reaction on other firm of the action or any
particular strategy adopted by one firm. There is an idea that firms operating in monopolistic
market environment applies is that “More could be sold by lowering the prices” and thus it is
considered as a popular economic concept of the contemporary world. The payoffs that is what
revenue does the two firms will generate as a result of their own and other firm’s pricing strategy
will be determined by keeping in mind the underlying economic concepts.
Two Game matrices based on social dilemma
Descriptive payoff matrix

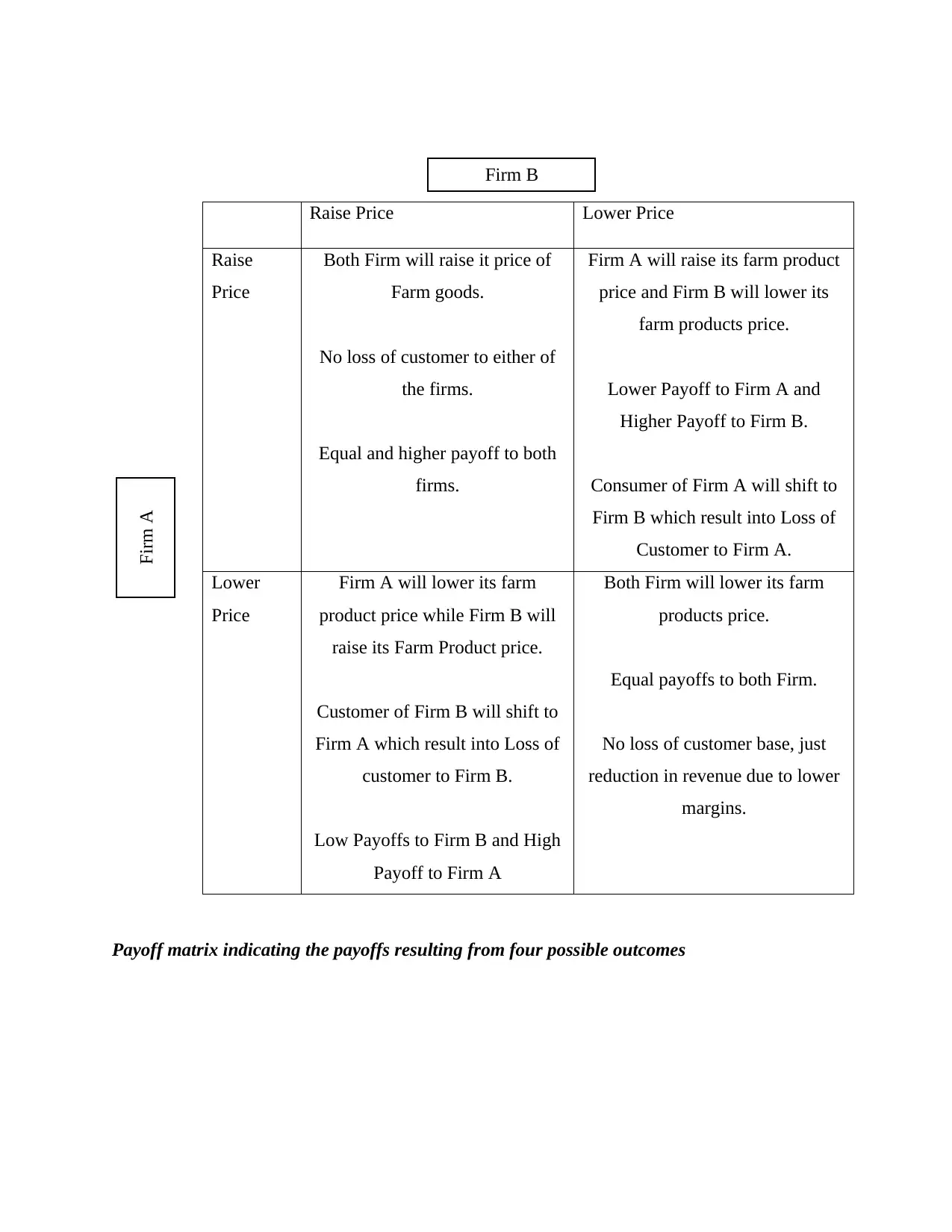
Raise Price Lower Price
Raise
Price
Both Firm will raise it price of
Farm goods.
No loss of customer to either of
the firms.
Equal and higher payoff to both
firms.
Firm A will raise its farm product
price and Firm B will lower its
farm products price.
Lower Payoff to Firm A and
Higher Payoff to Firm B.
Consumer of Firm A will shift to
Firm B which result into Loss of
Customer to Firm A.
Lower
Price
Firm A will lower its farm
product price while Firm B will
raise its Farm Product price.
Customer of Firm B will shift to
Firm A which result into Loss of
customer to Firm B.
Low Payoffs to Firm B and High
Payoff to Firm A
Both Firm will lower its farm
products price.
Equal payoffs to both Firm.
No loss of customer base, just
reduction in revenue due to lower
margins.
Payoff matrix indicating the payoffs resulting from four possible outcomes
Firm B
Firm A

Raise Price Lower Price
Raise
Price
Both Firm get £80 million
Firm A gets £40 million
Firm B gets £120 million
Lower
Price Firm A gets £120 million
Firm B gets £40 million Both Firm get £60 million
Explanation of payoffs assigned to each strategy and outcome their relevance with the social
dilemma
With reference to the given scenario, the payoff matrices have been developed for both
the firms on considering the impact of their own strategy and the strategy adopted by competitive
firm. There are four outcomes that could be seen through the above payoff matrix (Lee, Seo and
Kim, 2019). The first quadrant showing equal and higher payoffs to each of the firms where they
are raising their prices which results in equally sharing the market demand for the farm goods.
Therefore, the revenues for both the firms are equal. In the second quadrant, the pricing strategy
adopted by the two firms are different where firm A is raising price while firm B is lowering the
price of the farm goods. Accordingly, the revenues that firm A has generated is lower than that
of revenue generated by firm B because customers of firm A shifted to firm B for getting their
necessities at a cheaper rate. In the third quadrant, firm A has lowered the price while firm B has
raised the price of the farm goods. As a result of these counter strategy of two firms, firm A has
attracted the customers of firm B because the former’s price is lower and the latter’s price is
higher. The reason behind such shifting of customers from one firm to another firm is that in
monopolistic market, the products offered by different firms are close substitute of each other
Firm B
Firm A

(Li, Zhang and Perc, 2018). Therefore, it makes no difference for customers that from whom
they are making purchases and it is obvious that they will buy product at lower price instead of
higher price. In the fourth quadrant of the above matrix, the strategy adopted by both the firms
are again the same where strategy of lowering prices of farm goods has been adopted by firm A
and firm B. Accordingly, the revenue generated by both of the firms would be equal as indicated
by equal payoffs and there would be no loss of customers for either of the firms. However,
overall revenue would be less because in case of lower prices, the profit margins of firms are
lower and eventually revenue get reduced.
Rules of the game
The rule of the present social dilemma game is such as follows:
Players: There are two players in the game that is Firm A and Firm B. Both firm deals in a farm
products and operated in monopolistic competition market.
Payoff: Both Firm A and Firm B wants to maximize its payoff or profit.
Strategies: The strategic of Firm B depends upon the strategy adopt by Firm A to maximize its
profit. The action of firm B is depending upon the action of Firm A.
Timing of moves: The moves of the game are sequential because the move of Firm B is
influenced by the moves of Firm A.
Information set: In the game both Firm A and Firm B wants to maximize its payoff by deciding
either high price or low price of their Farm goods.
Equilibrium: This is the point in the game where both firms have made their own decision and
reached a desired outcome.
Concept of dominant strategy, Nash equilibrium and self – interested behavior
Concept of Dominant Strategy:
In game theory, dominant strategy is a situation where one player has a superior tactic
regardless of the other player’s actions. It means dominant strategy is one player action that does
not depends upon the other player actions or firm strategy. For example, Firm A and Firm B
wants to maximize its revenue or payoff and in order to do so they have two strategies such as
raising the price or lowering the price (Wang and et.al., 2018). The dominant strategy of both

Firm A and Firm B is to lower the price of its farm product in order to maximize its revenue. For
example, in case of Firm A, if both firm A and firm B will raise its price than, firm A will get
payoff or revenue of £80 million and if firm A reduce its price while firm B raise its price, in that
case firm A will get payoff of £120 million. After comparing this situation, it is identified that
£120 million payoffs are greater which is result of lowering price strategy. On the same side, if
firm A raise its price and firm B reduce its price, then firm A will get payoff of £40 million and
in case if both firm reduces its price than firm A will get pay off of £75 million. On this basis, it
is identified that £75 million is higher which is result of lowering the price strategy. Hence, as
per dominant strategy matrix, it is analyzed that the dominant strategy of Firm A is to lower the
price of its farm products.
While on the other hand, in the case of Firm B, if both firm lower its price than firm B
will get payoff of £80 million and if firm A raise its price and simultaneously firm B reduce its
price than firm B will get payoff of £120 million. After comparing the two result or outcome, it
is identified that £120 million is greater which is result of lowering the price strategy. On the
same side, if firm A will reduce its price and firm B raise its price simultaneously, then firm B
will get pay off of £40 million and if both firm lower its price than firm B will get pay off of £75
million. Out of which £75 million is higher which is basically a result of lowering the price of
farm products by Firm B (Sandholm, 2020). Hence, on the basis of decision matrix, it is
identified that the dominant strategy of firm B is to lower its price. The dominant strategy is
fulfilling the rule of monopolistic competition market which indicate that when one company
raise its price than their revenue will decreases because of loss of customer and vice-versa. This
is also known as dominant strategy equilibrium because both firm choses to lower its price of
farm products in order to maximize its payoff.
Concept of Nash Equilibrium:
In game theory, Nash equilibrium is a concept which state the point or situation of
optimal outcome of the game where each player will get no incentive by deviating from their
initial strategy (Wang and Chen, 2018). In other word Nash equilibrium is a decision-making
theorem within game theory where both players can achieve the desired level of outcome by not
deviating from their initial strategy. For example, in present game, both firm A and firm B level
of output will enhance with the reduction in the price of its farm product. Also, both the firm will

get equal payoff and no customer loss is to either firm at the situation when they both will not
deviate from its initial strategy of reducing price of its farm products. Hence, the Nash
equilibrium in the present case is where both firm A and firm B will reduce its price of farm
products and get equal pay off or revenue £75 million.
Concept of self-interested behavior:
Self-interested behavior in the game theory means the behavior of the player to do what
they want to do rather than affecting by other player action. In simple term, the self-interest
behavior means the player seek their own personal gains rather than considering the action of
their decision over other player (Zheng and et.al., 2018). For example, in the present game, firm
A will adopt strategy of lowering its price in order to earn revenue of £120 despite considering
its effect over the firm B where firm B revenue will reduce to £40 million because of this action
of firm A. This indicate the self-interested behavior of firm based on seeking their own personal
gain.
Description of Nash equilibrium, explanation of predicted outcome and its comparison with
socially desired outcome
In the given game, it has been seen that firms are adopting those possible strategies which
results in highest payoffs to them regardless of what other firms are doing. Each player is having
their own dominant strategy and thus dominant strategy equilibrium prevails. But this case may
not always be true and it becomes necessary to take actions by considering what others are doing
(Tanimoto, 2019). Accordingly, prediction of economic outcomes could be done by enhancing
the understanding of game theory. Here comes the concept of Nash Equilibrium which involves
adoption of particular strategy by all the firms given what other firms are doing. In other words,
when each players (firms) are responding in the best possible manner with respect to the
strategies adopted by other players or firms, it is known as Nash equilibrium.
In the given case of firm A and firm B, a dominant strategy equilibrium is achieved when
both the firms chooses their best or dominant strategy. The dominant strategy of both the firm
has been predicted as to lower the prices and thus there prevails a dominant strategy equilibrium.
It must be noted here that when there is a condition of dominant strategy equilibrium exists, then
there is always a Nash equilibrium. But all Nash equilibrium are not regarded as a situation of
dominant strategy equilibrium.

Therefore, in the current scenario, there exists the condition of dominant strategy
equilibrium and thus it is only the Nash equilibrium where both firms are lowering their prices
knowing that what other firm is doing (Zimmermann and et.al., 2018). It is true for the given
scenario of monopolistic market, when firms resort to lowering their prices in order to attain their
respective desired level of output.
On comparing the predicted outcome with that of socially preferred outcome, it has been
identified in the given scenario that there exists no difference between the two outcome. It is
because the predicted outcome for the two monopolistic firms are identified as equal payoffs
where they are adopting the strategy of lowering prices. Accordingly, socially desired outcome
would be different if the firms are having different dominant strategies and there is a need for
cooperation among each other because of conflict of interest. There is no need to move towards
socially preferred outcome as the predicted outcome would result in equal / highest payoffs to
both the firms.
Overcoming the social dilemma by relating it to the payoff matrix
The social dilemma for this project report was choosing the right pricing strategy by
firms operating in monopolistic market. With the help of above payoff matrix, the dominant
strategy for the two firms that is, A and B has been identified which indicates superior tactics for
each of them regardless of what other firm is doing. Accordingly, the social dilemma could be
resolved by stating that the right pricing strategy for two monopolistic firms is to lower the prices
of their farm goods which is true in case of monopolistic market scenario. Furthermore, as the
condition of dominant strategy equilibrium facilitates that the predicted outcome as a result of
identified dominant strategies would lead to no conflict of interest among two firms and thus,
they would get equal gains or payoffs which is what the socially desired outcome (Mazumdar,
Jordan and Sastry, 2019).
Success of proposed solution in motivating players towards socially optimal outcome
On the basis of game theory, it is identified that the successful solution proposed to both
firm is that they will adopt the strategy of lowering its price in order to meet their own desired
outcome of maximized revenue. While on the other hand, the socially optimal outcome also
indicates that, in monopolistic competitive market, the company should lower its price in order to
gain large customer base and increase the level of output which ultimately result into the increase

in revenue of business (Lee, 2018). There is basically no difference between the proposed
solutions and socially optimal outcome. Hence, on this basis, it can be said that the proposed
solutions are highly successful in motivating the players towards the socially optimal outcome as
well. It is because in monopolistic competition market, customers frequently shift to other firm in
the situation when its exiting firm raise the price of its products. Thus, to protect and retain its
customer base, it is important for the company to lower its price as it is socially optimal
outcome.
Effect of non – cooperative interactions on social dilemma and its potentiality in overcoming the
stated social dilemma
Non – cooperative interactions refer to the actions such as those taken by government
which may lead to resolving social dilemma or may affect social dilemma severely. For instance,
if there exists government’s interference in the fixation of prices of farm goods in order to
protect the interests of farmers from the actions and strategies of large firms. Accordingly, the
government generally resort to price floor where they fix minimum price for the farm goods and
no firm could be able to sell their produce lower than that (Flokas and et.al., 2020). As a result,
of this social dilemma of choosing the right price could be overcome because there exists a
standard for setting the price to be competitive and profitable in the market. So, it can be said
that social dilemma of maximizing payoffs could not be overcome while the dilemma of what
price should be set for the farm goods can be easily overcome.
CONCLUSION
After summing up the above information, it has been concluded that pricing decision of
firm in monopolistic competition market is a social dilemma. With the help of payoff, matrix it
has been concluded that both firm A and firm B dominant strategy is lowering the price of farm
products. This is also known as dominant strategy equilibrium and Nash equilibrium. Lastly, it
has been also concluded that the proposed solution is same as socially optimal outcome.

REFERENCES
Books and Journals
Azis, I. J., 2022. Agglomeration, Institution, and Social Capital: Main Concepts and
Methodologies. In Periphery and Small Ones Matter (pp. 35-56). Springer, Singapore.
Bertoletti, P. and Etro, F., 2022. Monopolistic competition, as you like it. Economic
Inquiry, 60(1), pp.293-319.
Flokas, L., and et.al., 2020. No-regret learning and mixed Nash equilibria: They do not
mix. arXiv preprint arXiv:2010.09514.
Ge, H. and Berry, R. A., 2018, October. Quantized dominant strategy mechanisms with
constrained marginal valuations. In 2018 56th Annual Allerton Conference on
Communication, Control, and Computing (Allerton) (pp. 590-595). IEEE.
Lee, C. Y., 2018. Mixed-strategy Nash equilibrium in data envelopment analysis. European
Journal of Operational Research. 266(3). pp.1013-1024.
Lee, E., Seo, Y. D. and Kim, Y. G., 2019. A Nash equilibrium based decision-making method
for internet of things. Journal of Ambient Intelligence and Humanized Computing, pp.1-
9.
Li, Y., Zhang, J. and Perc, M., 2018. Effects of compassion on the evolution of cooperation in
spatial social dilemmas. Applied Mathematics and Computation, 320, pp.437-443.
Mazumdar, E. V., Jordan, M. I. and Sastry, S. S., 2019. On finding local nash equilibria (and
only local nash equilibria) in zero-sum games. arXiv preprint arXiv:1901.00838.
Papadimitriou, C. and Piliouras, G., 2018. From nash equilibria to chain recurrent sets: An
algorithmic solution concept for game theory. Entropy. 20(10). p.782.
Ridley, D. and de Silva, A., 2020. Game Theoretic Choices Between Corrupt Dictatorship Exit
Emoluments and Nation-Building CDR Benefits: Is There a Nash Equilibrium?. The
American Economist. 65(1). pp.51-77.

Sandholm, W. H., 2020. Evolutionary game theory. Complex Social and Behavioral Systems:
Game Theory and Agent-Based Models, pp.573-608.
Tanimoto, J., 2019. Evolutionary games with sociophysics. Evolutionary Economics.
Wang, L. and Chen, Z., 2018. Nash equilibrium strategy for a DC pension plan with state-
dependent risk aversion: a multiperiod mean-variance framework. Discrete Dynamics in
Nature and Society. 2018.
Wang, L. and et.al., 2018. Strategy optimization for static games based on STP method. Applied
Mathematics and Computation. 316. pp.390-399.
Zheng, J. and et.al., 2018. Dynamic computation offloading for mobile cloud computing: A
stochastic game-theoretic approach. IEEE Transactions on Mobile Computing. 18(4).
pp.771-786.
Zimmermann, M., and et.al., 2018. Carrot and stick: A game-theoretic approach to motivate
cooperative driving through social interaction. Transportation Research Part C:
Emerging Technologies, 88, pp.159-175.