GEOG 2700 Fall 2018 Independent Assessment2

This assessment covers various statistical problems related to probability, sampling distribution, hypothesis testing, normality assumption, correlation test, non-parametric tests, and interpolation. It discusses different statistical tests and their applications in real-life scenarios. The output is in JSON format.

GEOG 2700
Fall 2018 Independent Assessment2
1

PART 1
1.01 Let p = probability of accident occurring = 1/10, n = drive through this intersection = 10
times per week, and X = Number of accidents in a week. Hence, required probability of
involving in an accident =
P ( X >0 ) =1−P ( X=0 ) =
1− ( 10 C0 )∗( 1
10 )
0
∗( 9
10 )
10
=1− ( 0 . 9 ) 10=0 . 6513
1.02 Let, L = lightning strikes, F = fire will occur in the grassland. Now, P ( L ) = 1
20 =0 .05 and
P ( F / L ) =0 . 25 . Therefore, P ( F∩L ) =0 .05∗0 . 25=0 . 0125 = probability that a lightning-
related fire will occur in any 1 km2. Total grassland preserve = 10 km2. Hence, n = 10.
Now, required probability of lightning-related fire will occur in the grassland preserve =
P ( X >0 ) =1−P ( X=0 ) = 1− ( 10 C0 )∗( 0 . 0125 ) 0∗( 0 . 9875 ) 10=1− ( 0 .9875 ) 10=0 .1182
1.03 Given that X ~ N ( 10 ,22 ) , Hence according to the problem P ( X < x ) =0 . 6
So,
P ( Z< x−10
2 )=0 . 6=P ( Z< 0. 25335 ) => x =10+2∗0 . 25335=10 . 5067≃10 . 51
Hence, x = 10.51 represents the lower 60% quantile.
1.04 Given that X ~ t (−2,0 . 32 ) , Hence according to the problem we need to find P ( X≤−1 )
Now,
P ( X≤−1 ) =P ( t≤−1+ 2
0 . 3 )=P ( t≤3 .33 ) =P ( Z≤3 . 33 ) =0. 9996
for unknown degrees of
freedom
1.05 Stratified random sampling would be used to collect the information separately from
students and faculties, regarding the distance travelled from the parking spot to their
respective campus. The average distance travelled by the two strata subjects will be then
tested for equality with proper choice of statistic.
1.06 Results in outcomes of sample statistics is defined or described by probability
distributions. Again, a statistic describes a set of values or data where data points come
from values of random variables. Hence, sample statistics are considered to be random
variables due to association of probability with observations.
2

1.07 Sampling distribution of the population mean is a distribution of statistics of group of
samples with a set of probability rules explaining the variation of behavior of the
samples. For example, sampling distribution of sample means or sample standard
deviations denote the probability distribution of statistic of samples.
1.08 Central limit theorem describes that for large value of the sample size (n>30), the
distribution of binomially distributed population mean follows a normal distribution with
sample value for the mean statistic.
1.09 Equations defining the requisite distribution will be μ= p
^¿
¿ and
σ ¿ ¿ , where
p
^¿
¿ the sample proportion and “n” is is the sample size. The population proportion is
distributed with mean μ and standard deviation σ .
1.10 According to the problem, n=150 , p=17
150 =0. 113 . The 95% confidence interval of the
proportion of customers is calculated as
CI =p±z0. 025∗
√ p ( 1− p )
n =0 . 113±1 . 96∗ √ 0 .113∗0 . 887
150 =[0 . 063 , 0. 163 ] . Hence,
0 . 063≤π≤0. 163 and it is estimated that proportion of customers with food allergies will
be somewhere between 0.063 and 0.163
1.11 According to the problem, n=150 , x
¿
=1200 , s=50
So the 90% confidence interval was evaluated using the formula
CI =x
−
±t0. 05∗ s
√ n =1200±1 . 64∗50
√ 150 =[1193 . 28 ,1206 . 72] where t-statistics was calculated
for 149 degrees of freedom for the probability of 0.90 within the confidence interval.
Hence, 1193. 28≤μ≤1206 . 72 estimates the population mean with 90% confidence.
3

1.12 Let X denotes the household gas usage with normally distributed probability distribution,
where standard deviation s=100 liters. Now standard error was specified as ±20 liters.
Hence, at 99% confidence level the standard of error is calculated as
± s
√ n =±20=> n=25
. So, 25 households must be taken as the sample to estimate the household gas supply.
1.13 The variable should be continuous in nature and should follow normal distribution. The
data for the variable should have been collected as a random sample from the population
data, and the observations should be independent of each other.
1.14 Size of sample = n=150 and the sample proportion is p
^¿= 3
15 = 1
5
¿ =0.2
(1) The claim can be tested by a left tail alternate hypothesis at 5% level of significance by z-
test for one sample proportion.
(2) Step 1: The null hypothesis H0: ( p=0 . 25 )
Step 2: Alternate hypothesis HA: ( p<0 .25 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: One sample z-test.
z−stat= p
^¿− p
√ p( 1− p )
n
= 0 . 2−0 . 25
√ 0 . 25∗0 .75
150
=−1 . 414 ¿
Step 5: The p-value is calculated as P ( z <−1 . 414 ) =0 . 0786
Step 6: The p-value was greater than α =0 . 05 and the null hypothesis failed to get rejected.
Hence, the proportion was not significantly less than 0.25.
1.15 Size of sample = 30 and the sample mean is x
¿
=210 and s=30
(1) The claim can be tested by a right tail alternate hypothesis at 5% level of significance by
one sample t-test.
(2) Step 1: The null hypothesis H0: ( μ=200 )
Step 2: Alternate hypothesis HA: ( μ>200 )
Step 3: Level of significance α=5 %=0 . 05
4

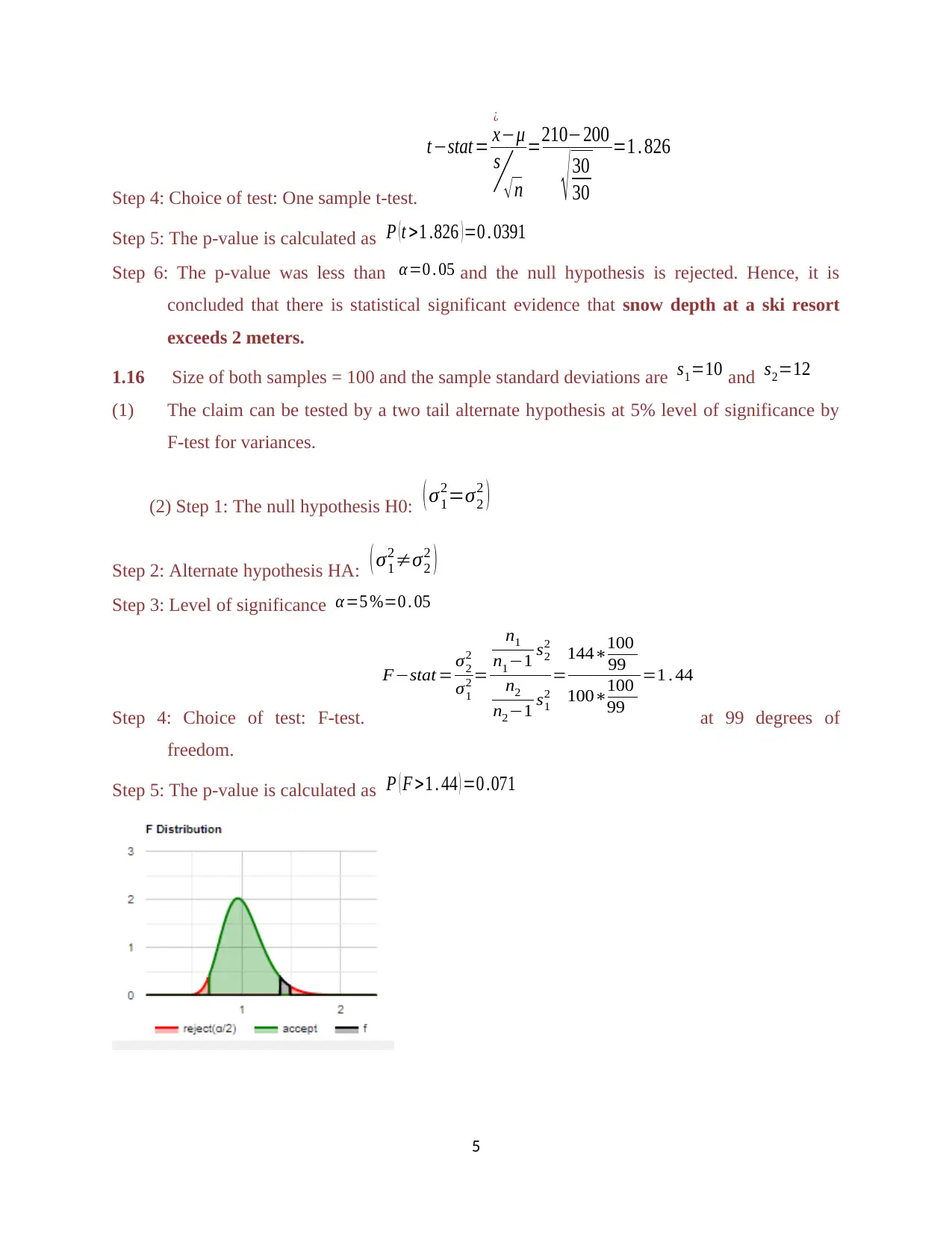
Step 4: Choice of test: One sample t-test.
t−stat = x
¿
−μ
s
√ n
=210−200
√ 30
30
=1 . 826
Step 5: The p-value is calculated as P ( t >1 .826 ) =0 . 0391
Step 6: The p-value was less than α =0 . 05 and the null hypothesis is rejected. Hence, it is
concluded that there is statistical significant evidence that snow depth at a ski resort
exceeds 2 meters.
1.16 Size of both samples = 100 and the sample standard deviations are s1=10 and s2=12
(1) The claim can be tested by a two tail alternate hypothesis at 5% level of significance by
F-test for variances.
(2) Step 1: The null hypothesis H0: ( σ1
2=σ2
2 )
Step 2: Alternate hypothesis HA: ( σ1
2≠σ2
2 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: F-test.
F−stat = σ2
2
σ1
2 =
n1
n1−1 s2
2
n2
n2−1 s1
2
=
144∗100
99
100∗100
99
=1 . 44
at 99 degrees of
freedom.
Step 5: The p-value is calculated as P ( F >1 . 44 ) =0 .071
5

Step 6: The p-value was greater than α=0 . 05 and the null hypothesis failed to get rejected.
Hence, it is concluded that there is not enough statistical significant evidence for
difference in variation in summer temperature between the two time periods.
1.17 Size of samples are n1=65 , n2=36
Sample means are x
¿
1=5100 , x
¿
2=5750 standard deviations are s1=300 and s2=600
(1) The claim can be tested by a right tail alternate hypothesis at 5% level of significance by
t-test for difference between means.
(2) Step 1: The null hypothesis H0: ( μ2−μ1=μd=500 )
Step 2: Alternate hypothesis HA: ( μ2−μ1>500 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: t-test for difference.
t−stat = x2−x1−μd
SE =5750−5100−500
106 .70 =0 .9372 where pooled standard deviation is
SE= √ s1
2
n1
+ s2
2
n2
= √ 3002
65 + 6002
36 =106 .70
Step 5: The p-value is calculated as P ( t >0 . 9372 ) =0 . 1768
Step 6: The p-value was greater than α=0 . 05 and the null hypothesis failed to get rejected.
Hence, it is concluded that there is not enough statistical significant evidence to claim
that sales have increased by at least $ 500.
1.18 Size of sample is n1=500 and the sample proportion is p
^¿1=47
50 =0. 94
¿ and n 2=760 and
the sample proportion is p
^¿2=605
760 =0 .796
¿
(1) The claim can be tested by a right tail alternate hypothesis at 5% level of significance by
z-test for difference of two sample proportions.
(2) Step 1: The null hypothesis H0: ( p1− p2=pd=0 . 1 )
6

Step 2: Alternate hypothesis HA: ( p1− p2=pd >0 .1 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: z-test. z−stat= p
^¿1− p
^¿
2−p
d
SE
=0 . 94−0 . 796−0. 1
SE =2. 718 ¿ ¿ Where pooled
standard deviation is
SE= √ p1 ( 1− p1 )
n1
+ p2 ( 1−p2 )
n1
= √ 0 .94∗0. 06
500 + 0 .796∗0 . 204
760 =0 . 0162
Step 5: The p-value is calculated as P ( z >2 .718 ) < 0 .001
Step 6: The p-value was way less than α=0 . 05 and the null hypothesis is rejected. Hence,
proportion of multi-family residences has decreased significantly by at least 10%.
1.19 Type of statistical tests that could be used to evaluate the normality assumption of the
variable are: Shapiro Wilk test and Kolmogorov–Smirnov test.
1.20 Correlation test or Scatter plot can be used to test that the sample data are independent.
1.21 Likert scale variable responses are ordinal in nature where the numbers associated with
the options are not meaningful. Hence, for sample size less than 30 will ne not normal in
nature. But, sometimes for interval scale Likert data with observations greater than 30,
parametric tests can be used.
1.22 For non-normal variable, Non-parametric tests such as Wilcoxon Signed Rank test,
Mann–Whitney U test, and Kruskal-Wallis test are used.
1.23 We can use Wilcoxon Signed Rank Sum test or Mann-Whitney test to support the
assertion that men are represented as less approachable than women in advertisements.
1.24 Chi-Square test can be used to support the claim that the occurrence of floods in dismal
creek follows a binomial distribution.
1.25 The Nearest neighborhood interpolation is the simplest approach to interpolation.
Instead of calculating the average of some weighting criteria, this method simply
determines the nearest neighbor.
For bilinear interpolation, the average of each cell is determined based on four nearest original
cells. The average is linear and horizontal. This is good for general leveling, but the
average for the typical sections of the local peaks and valleys is low.
7

The weighted average of the inverted distance is also known and gives no estimates outside the
measurements. Prediction errors are not categorized. The best IDW result is obtained
when you take the local deviation that you want to simulate.
Each random point of the data set is searched for each point of the interpolation point to find the
next point of the interpolation point. This method consists of a relatively small number of
randomly assigned points, but can be used with a larger number of points.
1.26 For linear interpolation with two points the equation of the line can be find as
F=λf ( x2 ) + ( 1−λ ) f ( x1 ) where λ denotes the ratio of the distance of the interpolating point
from the provided points in the table. Here, λ=25
35 and F is the value of air temperature at
the interpolating point. Hence, F=25
35 ∗19+10
35 ∗18=18 .71 Celsius.
1.27 The Euclidean distances from the point (5, 2) are calculated in the following table.
X coordinate 1.2 2 7 5
Y coordinate 1 3 2 1
Distance 3.93 3.16 2 1
The nearest neighbor is (5, 1) with the minimum distance as D =1 unit. Hence cadmium
concentration at the location (x=5, y=2) is 0.7 using Nearest Interpolation method.
1.28 The inverse of the Euclidean distances from the point (5, 2) are calculated in the
following table using p = 1 and considered as weights.
X coordinate 1.2 2 7 5
Y coordinate 1 3 2 1
Weight 0.25 0.32 0.5 1
Hence cadmium concentration at the location (x=5, y=2) is calculated as
0. 25∗0 .3+ 0. 32∗0. 5+0 . 5∗0. 2+1∗0. 7
( 0 .25+ 0 .32+0 . 5+1 ) =0. 5
8

PART 2
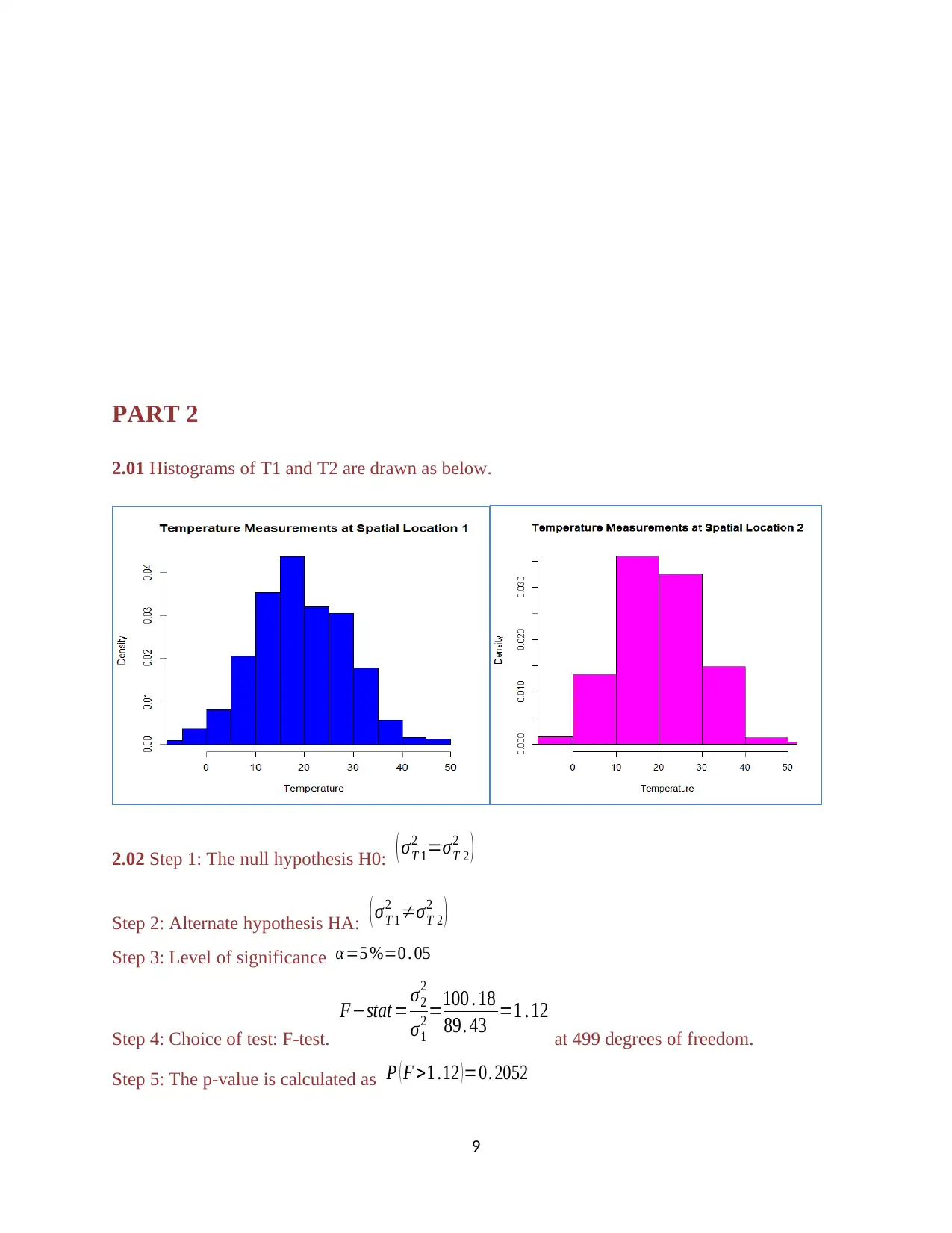
2.01 Histograms of T1 and T2 are drawn as below.
2.02 Step 1: The null hypothesis H0: ( σT 1
2 =σT 2
2 )
Step 2: Alternate hypothesis HA: ( σT 1
2 ≠σT 2
2 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: F-test.
F−stat = σ2
2
σ1
2 =100 . 18
89. 43 =1 . 12
at 499 degrees of freedom.
Step 5: The p-value is calculated as P ( F >1 .12 ) =0. 2052
9

Step 6: The p-value was greater than α=0 . 05 and the null hypothesis failed to get rejected.
Hence, it is concluded that there is not enough statistical significant evidence for
difference in variation in summer temperature between the two spatial locations.
2.03 Step 1: The null hypothesis H0: ( μ2=μ1 )
Step 2: Alternate hypothesis HA: ( μ2>μ1 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: t-test for difference.
t−stat = x2−x1
SE = 20 .. 254−19 .03
106 .70 =1 . 986 where pooled standard deviation is
SE= √ s1
2
n1
+ s2
2
n2
= √ 100. 18
500 +89. 432
500 =1 . 9863
Step 5: The p-value is calculated as P ( t >1 .98632 ) =0 . 0236
Step 6: The p-value was less than α =0 . 05 and the null hypothesis was rejected at 10%. Hence, it
is concluded that there is enough statistical significant evidence to claim that average
temperature at T2 was significantly greater than that of the T1 location.
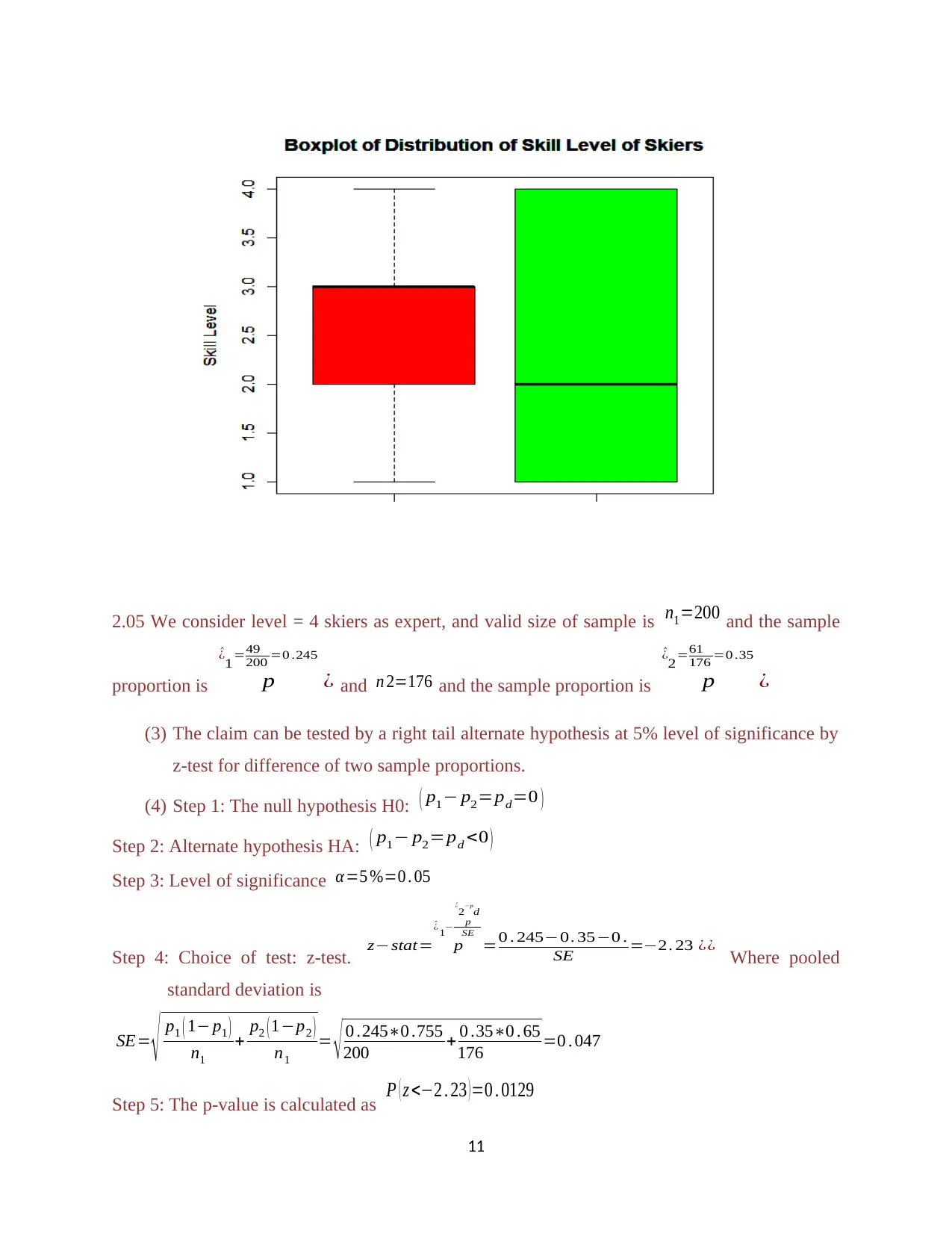
2.04 Box plots of the variables have been represented below.
10

2.05 We consider level = 4 skiers as expert, and valid size of sample is n1=200 and the sample
proportion is p
^¿1=49
200 =0 .245
¿ and n 2=176 and the sample proportion is p
^¿2=61
176 =0 .35
¿
(3) The claim can be tested by a right tail alternate hypothesis at 5% level of significance by
z-test for difference of two sample proportions.
(4) Step 1: The null hypothesis H0: ( p1− p2=pd=0 )
Step 2: Alternate hypothesis HA: ( p1− p2=pd <0 )
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test: z-test. z−stat= p
^¿1− p
^¿
2−p
d
SE
=0 . 245−0. 35−0 .
SE =−2. 23 ¿¿ Where pooled
standard deviation is
SE= √ p1 ( 1− p1 )
n1
+ p2 ( 1−p2 )
n1
= √ 0 .245∗0 .755
200 + 0 .35∗0 . 65
176 =0 . 047
Step 5: The p-value is calculated as P ( z <−2 . 23 ) =0 . 0129
11

Using R command pnorm(-2.23, lower.tail=TRUE)
Step 6: The p-value was way less than α=0 . 05 and the null hypothesis is rejected. Hence,
proportion of level 4 expert skiers was significantly greater in place N1.
2.06 The 5-number summary of the variable Sat00 is in the following table.
2.07 The Interquartile Range was calculated in R as Q3-Q1= 1 for Sat000.
2.08 The inner fence is known as= Q1−1. 5∗IQR=3−1 . 5∗1=1. 5
12

A single outlier value was observed for Satisfaction in 2000.
2.09 Step 1: The null hypothesis for skiers’ satisfaction is H 0: π =4
Step 2: The alternate hypothesis is H 0: π < 4 .
Step 3: Level of significance α=5 %=0 . 05
Step 4: Choice of test one tail Signs-test.
Sign−stat=B=38 Is the number of positively satisfied subjects with the binomial null
hypothesis is H0: p=0 . 5 with n = 75
13

Step 5: The statistic value is B = 38, with the p-value calculated as p = 0.59 using R-command
pbinom (38,75,0.5)
Step 6: The p-value was greater than α=0 . 05 and the null hypothesis failed to get rejected at 5%
level.
.
2.10 In 2000, the satisfied skiers were 38 in numbers and this reduced to 21 in 2015. The median
of the two samples were evaluated as ( η2=3∧η1=4 )
Step 1: Hence, the null hypothesis is H0: ( η2=η1 )
Step 2: And the left tailed Alternate hypothesis is HA: ( η2 <η1 )
Step 3: Level of significance is α=5 %=0 . 05
Step 4: Choice of test: Mann-Whitney test for difference in satisfaction for 2000 and 2015.
We know compute the sum of the ranks of the two samples and rephrase the hypotheses in terms
of the test variable (“W”) as
H0: ( W 2=μw )
HA: ( W 2 < μw )
We know that the statistic W is normally distributed and the mean and standard deviation can be
evaluated as follows,
μw =n2 ( n2 +n1+1 )
2 = 75 ( 75+75+1 )
2 =5662.5
And
σ S
2= n2 n1 ( n2 +n1 +1 )
12 = 75∗75 ( 75+75+1 )
12 =70,781.25
¿> σS
❑=266.05
Now we tabulate the data and calculate the sum of the ranks as below.
14

Respons
e Sat00 Sat15
Average
Rank
1 20 11 10.5
2 21 13 31
3 34 30 66.5
4 0 20 116
5 0 1 145.5
The sum of the ranks for 2015 is =
W =11∗10.5+13∗31+30∗66.5+20∗116+ 1∗145.5=4979
Step 5: Hence, the z−stat=4979−5662 .5
266 . 05 =−2 .57
The p-value is calculated as P ( z <−2 . 57 ) =0 . 0051
Using R-command pnorm (-2.57, lower.tail =TRUE)
Step 6: The p-value was less than α=0 . 05 and the null hypothesis was rejected at 10%. Hence, it
is concluded that there is enough statistical significant evidence to claim that skiers were
satisfied more in 2000 compared to 2015.
15