Determination of Gravitational Force using Simple Pendulum

Learn how to measure acceleration due to gravity using a simple pendulum experiment. The article covers the problem statement, what is known about the problem, what is needed to solve the problem, materials needed, method, results, error calculation, and possible sources of errors. The output is in JSON format.

PBL Assignment: simple pendulum 1
Problem Title: Determination of gravitational force using simple pendulum
Date:
Team members
1)
2)
3)
Section 1: Problem statement
The problem we assumed understand is to measure the acceleration because of gravity
by the utilization of a string and mass to make a pendulum. This issue is achievable just by
doling out the group individuals to discover fundamental materials that will enable us to find
out the best way to determine acceleration due gravity. We will concoct an exact examination
to tackle the problem
.Section 2: What we know about the problem
Gravitational pull is the force that brings two bodies towards one another [1], the
force that makes celestial bodies to orbit around the sun and also makes things to fall onto the
ground level. However, if the object has a greater mass, it possess the strongest gravitational
pull. Gravity is amongst the most important forces on earth. This is because it makes object to
have weight. For example, when one goes to weigh themselves, the weighing scale tells us
the amount of gravity on our bodies. To make this clear, one of the group members went to
weigh his body weight and we found out the mass was 55 kilograms.
Weight=mass of the body∗gravitational pull. Isaac Newton built up this theory of
universality gravitation in 1960s. The conclusion he made was that every matter was being
acted upon by force of gravity. The attraction of every other object is proportional to the
product of its masses and inversely proportional to the square of the distance apart. This can

PBL Assignment: simple pendulum 2
be shown as: Fg=G(m₁∗m₂)/r ² whereby: Fg is the gravitational pull, r is the apart distance
of the objects, m₁ , m₂ represents the two different masses and G represents the gravitational
pull constant.
Therefore, gravitational acceleration is the acceleration of the body due to the
influence of gravitational pull, denoted ‘g’ [2]. This value is very different for celestial
bodies. An example is the acceleration due to gravity for the earth is different from that of the
moon. In addition, acceleration possess direction and magnitude hence it is a vector quantity.
The direction is towards the centre of earth while the average magnitude of the value g is 9.8
m/s2, which simply means that when an object is falling freely, it experiences that speed that
increases every second.
Section 3: What we need to know to solve the problem
The data required in order to take care of the problem include;
 Knowledge on gravitational acceleration.
 Knowledge on simple pendulum experiment.
 Materials needed to perform the experiment.
 The correct method to conduct the experiment.
 Using excel software to draw graphs.
 How to best analyse the results
The work was separated similarly among three of us with the first individual from the
group inquiring about on the acceleration due to gravity and inferring the conditions included.
The second partner was to find how to perform the experiment by reading about the simple
pendulum experiments and furthermore to decide the kind of materials required. Our third
member in the group was to find out how to draw diagrams, the factors to be plotted and
accompanied the most ideal method for breaking down the outcomes. At that point, as the
group individuals we joined and did the analysis together.

PBL Assignment: simple pendulum 3
All of the research was typed and compiled step by step. We derived the gravitational
acceleration as shown. From Newton’s 2nd law of motion, F=ma whereby;
F is force acting upon the object
m represents the mass of the body
a is the acceleration
According to Newton’s Law of gravity, we can write the formula as;
Fg=GMm /(r + h) ² Whereby:
Fg Is the gravitational pull
m₁ , m₂ Represents the two different masses
r is the distance apart of the two objects
G represents the gravitational pull constant
h is the height
This is the force of gravity acting on two bodies that are lying in the field of gravitational pull
to each other [5]. The two bodies experience same force that is being directed to each other
with the same magnitude. In order to find the acceleration due to gravity, we can comfortably
use newton’s 2nd law; a=Fg/m [4].
Here, the mass of the object is m, and the acceleration due to gravitational pull will be
calculated.
a=g=GMm /( y + h) ² m
When the object is near the surface, the value of the gravitational pull ‘g’ becomes a
constant and it does not change [7].
Therefore we get; g=GM /r ² whereby;
G represents the gravitational pull constant
M is the mass of the objects
R is the distance apart of the masses

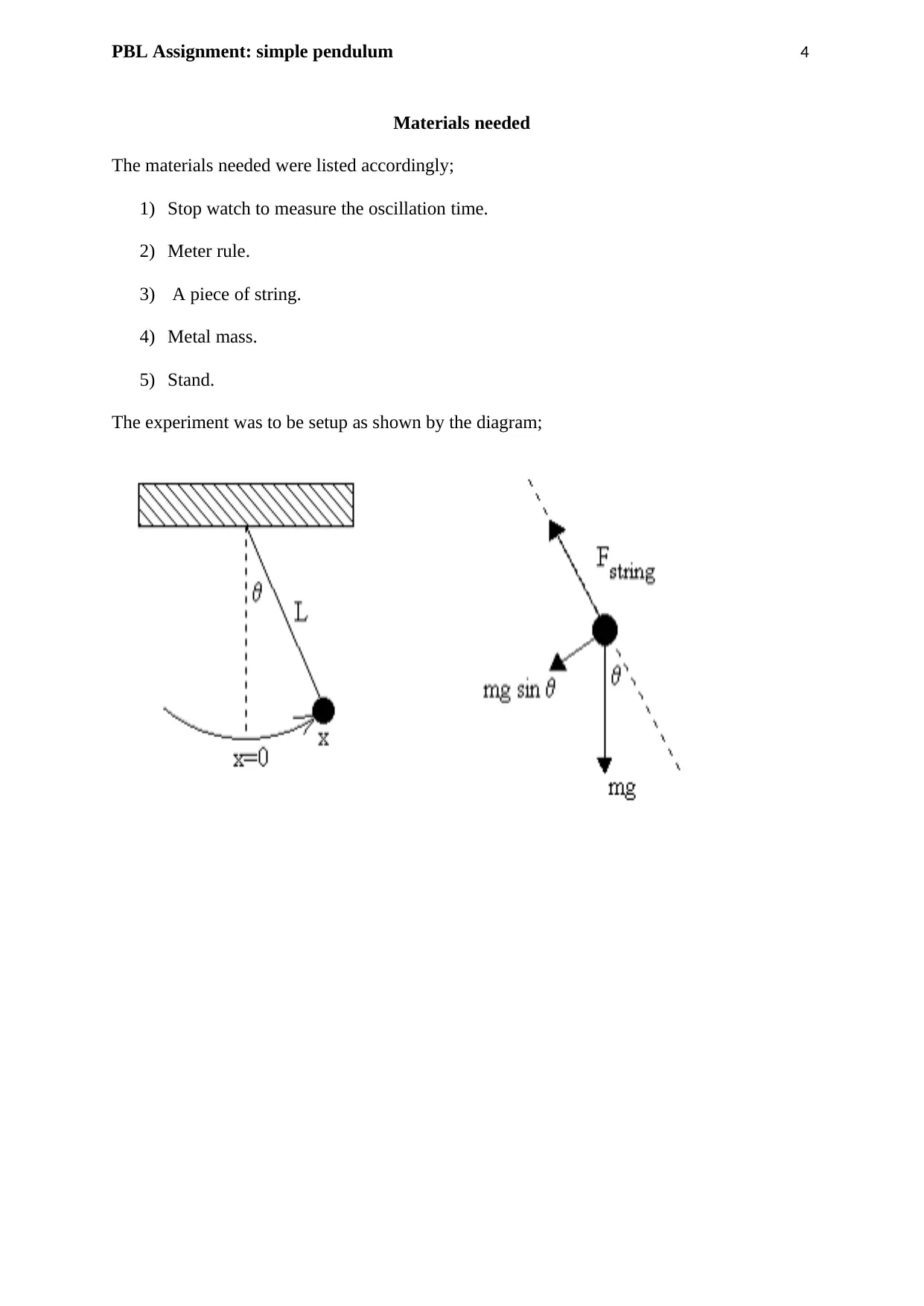
PBL Assignment: simple pendulum 4
Materials needed
The materials needed were listed accordingly;
1) Stop watch to measure the oscillation time.
2) Meter rule.
3) A piece of string.
4) Metal mass.
5) Stand.
The experiment was to be setup as shown by the diagram;

PBL Assignment: simple pendulum 5
Assumption to be made
 The chosen string was non-elastic.
 If a metallic pendulum used, the experiment will generate accurate results.
 The stand was stable.
Method
One of the group member connected the string to the pendulum and made sure that it
was in a position to swing uninhibitedly without making contact.
We first used 40 cm length of the string to perform the experiment. Then, we used 60
cm progressively till 120 cm length of the string. The values accrued were recorded by on the
table of results. An angle of 20 degrees was set and the string was released. Tallying the
number of oscillations began when the string balanced out. Around 20 oscillations were
estimated and the information recorded in the table. Progressive experiment were done in the
same while alternating the group members.
The values were tabulated and completed calculations were made amicably.
A graph of independent variable L and dependent variable T² drawn on the x and y axes
respectively.
The gradient of the graph was to be found by choosing at least two points within the line.
Precautions
 We needed to make sure that the pendulum was released with no of us giving an outer
push.
 We needed to ensure the string was straight before releasing it.

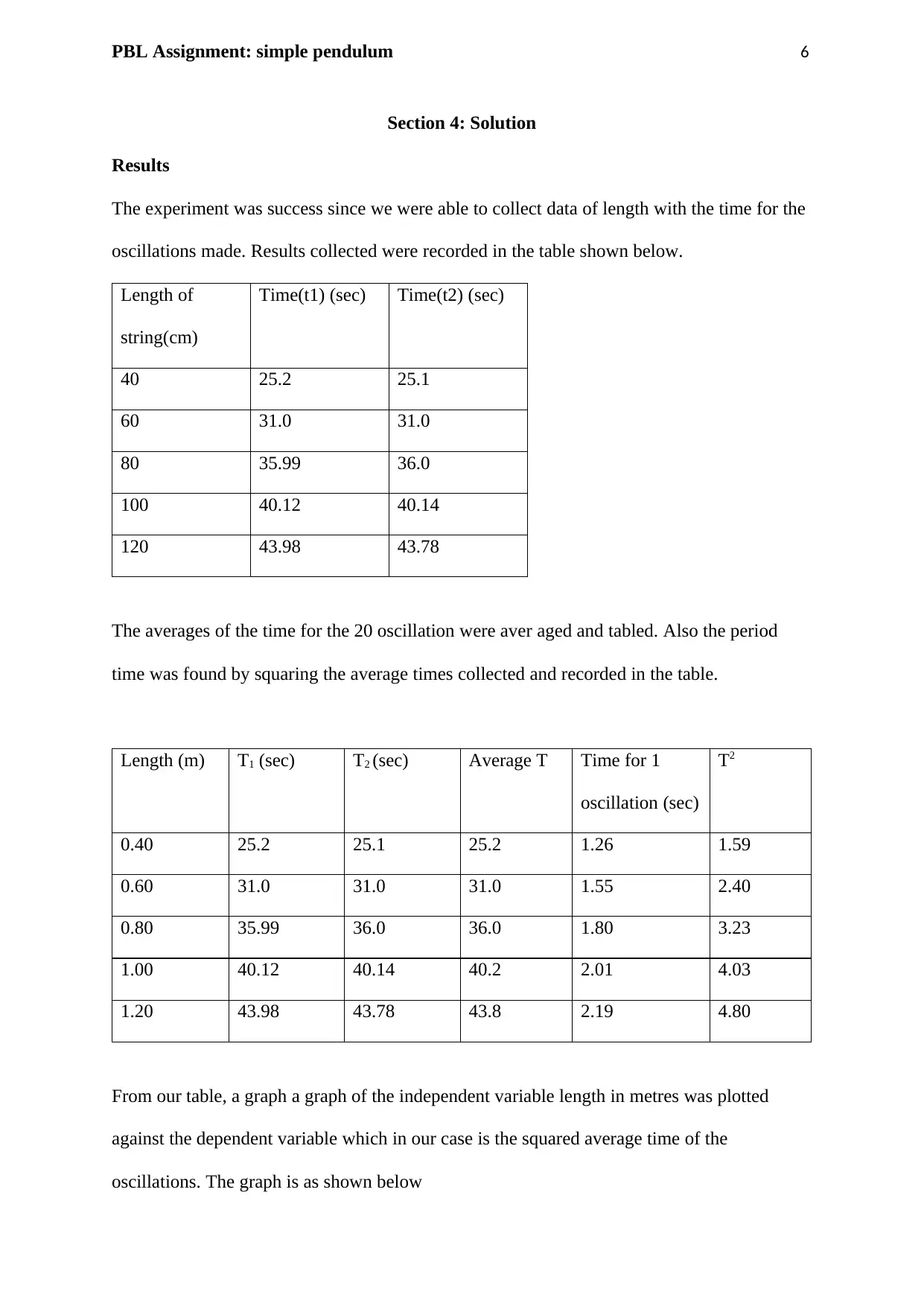
PBL Assignment: simple pendulum 6
Section 4: Solution
Results
The experiment was success since we were able to collect data of length with the time for the
oscillations made. Results collected were recorded in the table shown below.
Length of
string(cm)
Time(t1) (sec) Time(t2) (sec)
40 25.2 25.1
60 31.0 31.0
80 35.99 36.0
100 40.12 40.14
120 43.98 43.78
The averages of the time for the 20 oscillation were aver aged and tabled. Also the period
time was found by squaring the average times collected and recorded in the table.
Length (m) T1 (sec) T2 (sec) Average T Time for 1
oscillation (sec)
T2
0.40 25.2 25.1 25.2 1.26 1.59
0.60 31.0 31.0 31.0 1.55 2.40
0.80 35.99 36.0 36.0 1.80 3.23
1.00 40.12 40.14 40.2 2.01 4.03
1.20 43.98 43.78 43.8 2.19 4.80
From our table, a graph a graph of the independent variable length in metres was plotted
against the dependent variable which in our case is the squared average time of the
oscillations. The graph is as shown below

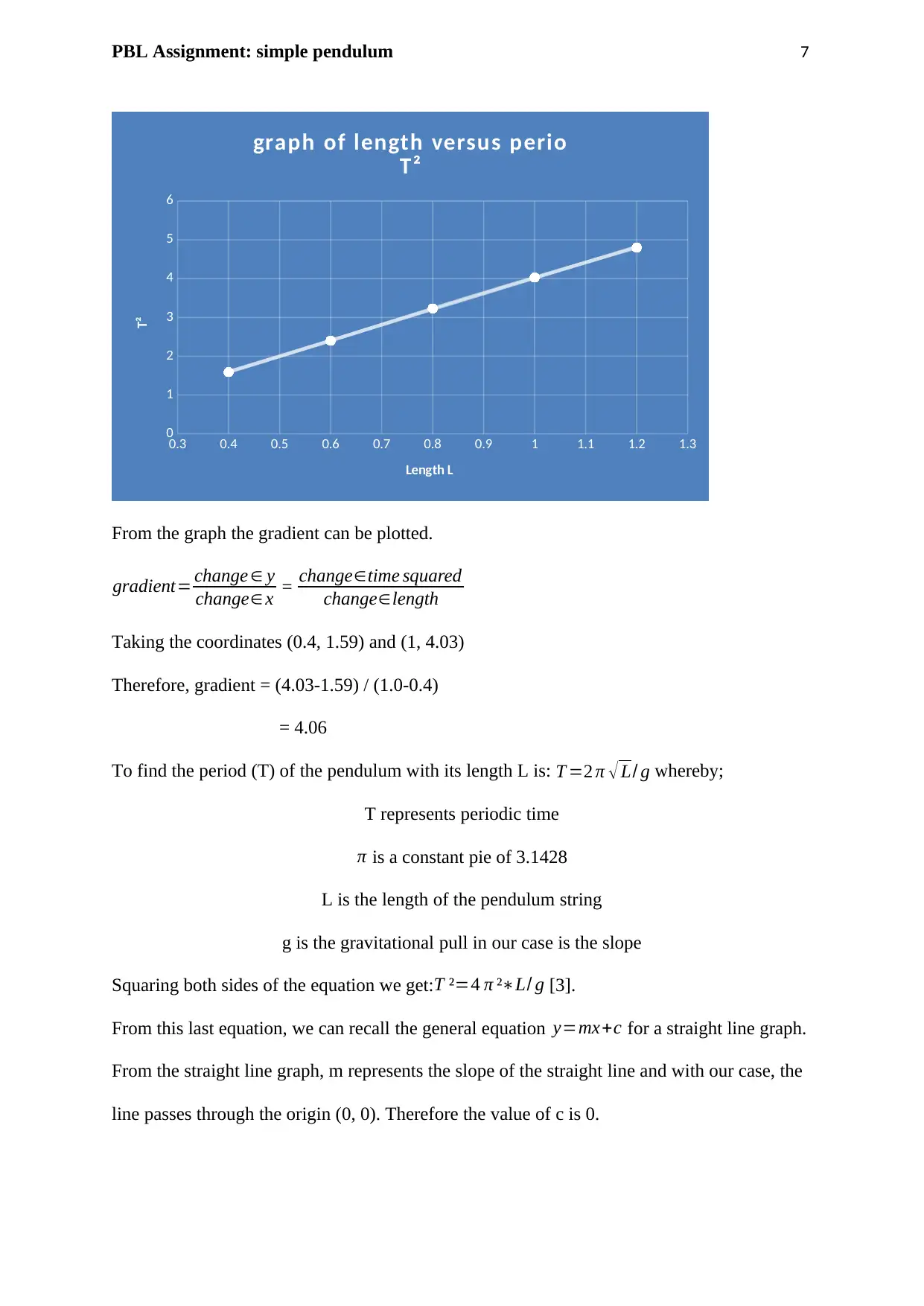
PBL Assignment: simple pendulum 7
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3
0
1
2
3
4
5
6
graph of length versus perio
T²
Length L
T²
From the graph the gradient can be plotted.
gradient= change ∈ y
change∈x = change∈time squared
change∈length
Taking the coordinates (0.4, 1.59) and (1, 4.03)
Therefore, gradient = (4.03-1.59) / (1.0-0.4)
= 4.06
To find the period (T) of the pendulum with its length L is: T =2 π √ L/ g whereby;
T represents periodic time
π is a constant pie of 3.1428
L is the length of the pendulum string
g is the gravitational pull in our case is the slope
Squaring both sides of the equation we get: T ²=4 π ²∗L/ g [3].
From this last equation, we can recall the general equation y=mx+c for a straight line graph.
From the straight line graph, m represents the slope of the straight line and with our case, the
line passes through the origin (0, 0). Therefore the value of c is 0.

PBL Assignment: simple pendulum 8
Substituting the terms from the line graph of the pendulum equation which has passed
through the origin to y=mx+0 since the constant c passes the origin if the straight line is
extrapolated further.
One of the group members calculated and it can be shown clearly below;
Slope of the graph = 4.06
L of the pendulum = 4.0
But, slope = 4 π ² /g
Therefore, g = 4 π ² /slope
= (4 * 3.1428²) / 4.06
g = 9.73 m/sec²
Therefore, 9.73 m/sec² was the gravitational acceleration found.
Error calculation
It is evident from calculation that, there is a slight deviation from the known
average value of acceleration due to gravity which is at 9.8 m/sec². We went ahead and our
group member suggested to show us how to find the error percentage since already had the
theoretical value of acceleration due to gravity and the experimental result which was 9.73
m/sec².
Percentage error = (experimental value – known value) known value * 100%
From our analysis, % error = (9.73 – 9.8) m/sec²
Error = -0.07 m/sec²
= -0.07 m/sec² / 9.8 m/sec²
= 0.007
% error = 0.007 * 100
= 0.7%

PBL Assignment: simple pendulum 9
Therefore, the percentage error was found to be 0.7%. This is a small error which might
b=have been caused during the experiment.
Possible sources of errors
 Limiting air friction might have limited the accuracy from the swinging point [6].
 One of the members might have given a slight push to the ball since everyone had to
participate in the experiment.
 Reaction time from the members might have caused errors.
 Rotation of the ball due to the effect of revolution of the earth. This might have
caused disturbances to the measures of counting the oscillations.
Conclusion
The estimation of the acceleration due to gravity was accomplished effectively
fulfilling the problem statement of research. We found the acceleration due to gravity to be
9.73 m/sec² which veered off from the known value with a rate blunder of 0.7%. Thinking
about the levels of error, high precision values will be obtained by limiting the response time.
More so, the quantity of oscillations will be increased keeping in mind the end goal to
decrease the errors due to timing [8].
REFERENCES

PBL Assignment: simple pendulum
10
[1]T. Ghose, "What Is Gravity?", Live Science, 2018. [Online]. Available:
https://www.livescience.com/37115-what-is-gravity.html. [Accessed: 05- Oct- 2018].
[2]S. AbdElazem and W. Al-Basheer, "Measuring the acceleration due to gravity using an IR
transceiver", European Journal of Physics, vol. 36, no. 4, p. 4, 2015.
[3]H. Parks and J. Faller, "Simple Pendulum Determination of the Gravitational
Constant", Physical Review Letters, vol. 105, no. 11, p. 15, 2010.
[4]M. Jewess, "Optimising the acceleration due to gravity on a planet's surface", The
Mathematical Gazette, vol. 94, no. 530, pp. 35=37, 2010.
[5]J. Cutnell and K. Johnson, Introduction to physics. London: John Wiley & Sons, 2010, pp.
102,110.
[6]B. Solomon, "Gravitational acceleration without mass and noninertia fields", Physics
Essays, vol. 24, no. 3, pp. 327-337, 2011.
[7]"Acceleration of Gravity", Physicsclassroom.com, 2018. [Online]. Available:
https://www.physicsclassroom.com/class/1DKin/Lesson-5/Acceleration-of-Gravity.
[Accessed: 06- Oct- 2018].
[8]Nano-optics.colorado.edu, 2018. [Online]. Available:
https://nano-optics.colorado.edu/fileadmin/Teaching/phys1140/lab_manuals/
LabManualM1.pdf. [Accessed: 06- Oct- 2018].