Heat Capacity Lab

This lab experiment focuses on measuring the heat transferred from copper to water using a calorimeter. It aims to determine the specific heat capacity of copper and the heat of formation of ammonium chloride. The experiment involves calorimetry and the application of Hess's Law. The results and calculations are provided.

Heat Capacity Lab 1
University Affiliation
Heat Capacity Lab
By
Name of Student
Date
Name of Lecturer

Heat Capacity Lab 2
Introduction
Part A
Calorimetry is the science of heat measurement. One of the intention of the lab was to
measure the heat transferred from copper to water using a calorimeter. Knowing the value of
specific heat of water would make it possible to compute the specific heat of copper in this
experiment. Heating a substance increases the motion or kinetic energy of its particles thus
increasing its temperature. When more heat is added to a given object raises its temperature
further. Specific heat is the relationship between the mass of the substance, the amount of heat
added and the change in its temperature.
A considerable amount of heat is needed to raise the temperature of a substance from a
lower temperature T1 to a higher temperature T2. This quantity of heat differ from one material to
another and it depends on a number of factors such as mass and specific heat of the material as
well as difference in temperature. Calometry involves measuring the quantities of heat.
Part B
In this part of the experiment the heat of solution of ammonium chloride (NH4Cl(s) ) as well as
the heat of neutralization of hydrochloric acid (HCl (aq) ) and ammonia (NH3 (aq) ) are to be
measured then combined with already determined heats of a number of reactions to find out
the heat of formation of NH4Cl(s) with the help of Hess' Law. For a chemical reaction to take
place, heat must be involved. A chemical reaction either involves loss of heat (exothermic) or
absorption of heat (endothermic). Heat of reaction for any cheamical reaction can be found using
the following procedure and chemical formula
∆ H =∑ ∆ H f ( prdoucts)−∑ ∆ H f (reactants)

Heat Capacity Lab 3
For exothermic reaction, heat is released to the surrounding and ∆ H has a negative value. For
endothermic reaction, heat is absorbed and ∆ H has a positive value. The negative value of ∆ H
indicates that the reactants are at a higher energy state than the products while a positive H
shows the reactants are at lower energy state than the products.
Objective
1. To determine the specific heat capacity of copper using a calorimeter
2. To find the Enthalpy of formation of ammonium chloride
Theory
Part A
Heat can be described as energy linked to the increased motions of atoms due to rise in its
temperature. When heat energy is basically added to a substance at constant pressure, the
temperature of that substance would rise (Signorelli, 2014). This is not the case only when there
is phase change (liquid is changing into a gaseous state, or solid is changing into the gaseous
state). A phase change usually happens without a decrease or increase in the temperature of the
substance. Heat cannot flow out or into objects in a vacuum or a place with no matter. Heat
requires matter to flow. Hence in a vacuum the temperature of an object remain the same
(Signorelli, 2014) (Signorelli, 2014). When two objects are brought into contact with one
another, heat will basically flow from the object that is hotter to the object that is cooler. It
implies that thermal energy of the hotter energy reduces and that of the cooler object increases.
The flow of heat between the two objects flows until both the objects attain constant temperature
(thermal equilibrium). This flow of heat in out or into an object which are in contact can be
explain using the concept of specific heat which attempts to explain the relationship between the
change in temperature of the objects and heat or thermal energy (Signorelli, 2014).

Heat Capacity Lab 4
Specific heat capacity is quantity of heat which is required to raise the temperature of a mass of
material by a kelvin. The specific heat capacity of a given substance is a physical property. On
the other hand it can be termed as quantity of heat required to increase one gram of a substance
or material by one kelvin. It is expressed as J/kg·K. In addition, specific heat capacity can be
measured in the units of calories per gram degree Celsius.
c= Q
∆ T
Where
c=heat capacity ,
Q=energy(¿ joules)∧¿
∆ T =temperature(¿ Kelvin∨degree Celsius)
Specific heat, is directky proportional to mass of a material mass:
c=m× S
In which
S=the specific heat capacity
M =mass of the material∧¿
C=the heat capacity
Finding specific heat of a metal in an experiment using methods of mixtures requires the
mas of the metal, its high temperature and mass of water to be known, The metal of a known
mass is thus dropped into the calorimeter. The after the equilibrium has been attained, the final

Heat Capacity Lab 5
temperature is thus measured. The heat absorbed by the calorimeter, stirrer, and water is equal to
the heat lost by the copper metal. The specific heat of copper can be calculated as follows
mc ( T −T 1 )=¿
In which
mc=mass of copper
T =Temperature of Copper
T 2=final temperature (eqilibrium)
T 1=initial calorimter ∧water temperature
mcal . Ccal=Ccal . which is the water equivalent of the stirrer ∧claorimter
mw=mass of cold water
Part B
According to Hess's Law of constant heat summation, irrespective of the many steps or
stages of a reaction, the total change in enthalpy for a reaction is the summation of all the
changes (Kotz, Treichel & Townsend, 2013). The standard of the heat of formation of a given
compound is the heat absorbed or released when the elements of the compounds in their standard
states form one mole of the compound. The standard heat of formation of ammonium chloride is
as below
First reaction: 1
2 N2 ( g ) + 2 H2 (g)+ 1
2 Cl2 ( g ) NH 4 Cl ( s)

Heat Capacity Lab 6
Since one mole of a compound is formed, the coefficient of the product is set to one,
hence some reactants have fractions (Kotz, Treichel & Townsend, 2013).
The heat of neutralization of HCl and NH3 heat of solution of NH4Cl(s) can be measured using
the experiment
2 nd Reaction : NH4 Cl (s)+Cl−1 ( aq)
3 rd Reaction: NH 3 ( aq ) + HCl ( aq ) → NH 4 Cl (aq)
They are then combined with the known heats for specific reactions to calculate the heat of
formation of ammonium chloride
Procedure
Part A
About 60g of copper was weighed and placed in a test tube. The test tube containing
copper was placed in a 600 mL beaker containing 400 mL of hot water. The beaker was then
placed on a hot pate and then heated. Once the water started boiling, the temperature was
slightly lowered to maintain gentle boiling point for about 60 minutes. The temperature of the
boiling water was then recorded. 60g of distilled water was weighed into the calorimeter and the
exact mass of water was recorded. The calorimeter lid was then fitted and a thermometer
inserted. The temperature readings were taken at an interval of 30 seconds. The specific heat
capacity of copper was then calculated and the graph was drawn.
Part B
50.0 mL, 2.0 M of ammonia solution was transferred by pipette to a calorimeter. The calorimeter
was set up and 50.0 mL, 2.0 M of HCl solution to the dropping funnel by a pipette. The ammonia
solution was stirred and the temperature in the calorimeter recorded at an interval of 30 seconds

Heat Capacity Lab 7
for about 5 minutes. HCl was then added to the calorimeter as quickly as possible and at once
and temperature continued to be recorded at an interval of 30 seconds and about six readings
recorded after the maximum is attained. The graph of temperature against time elapsed was
plotted and change in T1 of the reaction determine.
Data and Results
Part A
The initial temperature
of copper T1 = 45. 6
The initial temperature
of water and
calorimeter T2= 95.3 0C
The final temperature
of the water,
Calorimeter, and
copper T3= 46.97 0C
Part B
Table 2 (reaction 3)
Time (min:Sec) Temperature (0C) ln(temperature)
0.30 47 3.85
1.00 46.8 3.846
1.30 46.6 3.841
2.00 46.4 3.837
2.30 46.3 3.835
3.00 46.2 3.833
3.30 46.1 3.831
4.00 46.0 3.829
4.30 45.9 3.826
5.00 45.8 3.824
5.30
6.00
6.30
7.00
7.30
8.00
Time (min:Sec) Temperature (0C) ln(temperature)
0.30 22 3.09
1.00 29.9 3.398
1.30 30 3.401
2.00 31 3.434
2.30 31.2 3.444
3.00 31.8 3.459
3.30 32 3.466
4.00 32.1 3.469
4.30 32.2 3.472
5.00 32.5 3.4812

Heat Capacity Lab 8
0 1 2 3 4 5 6
2.8
2.9
3
3.1
3.2
3.3
3.4
3.5
3.6
f(x) = 0.0543612121212121 x + 3.26162666666667
R² = 0.502136605008279
ln(temperature vs. Time elapsed
Time in seconds
ln(temperature)
The y-intercept = 3.2616
The Final Temperature is thus, the exponential of y-intercept = 26.09
Table 3 (reaction 4)
Time (min:Sec) Temperature (0C) ln(temperature)
0.30 22.6 3. 118
1.00 22.6 3.118
1.30 22.6 3.118
2.00 20.3 3.011
2.30 20.2 3.01
3.00 20.1 3.0
3.30 19.1 2.95
4.00 19.1 2.95
4.30 19.0 2.94
5.00 19.0 2.94

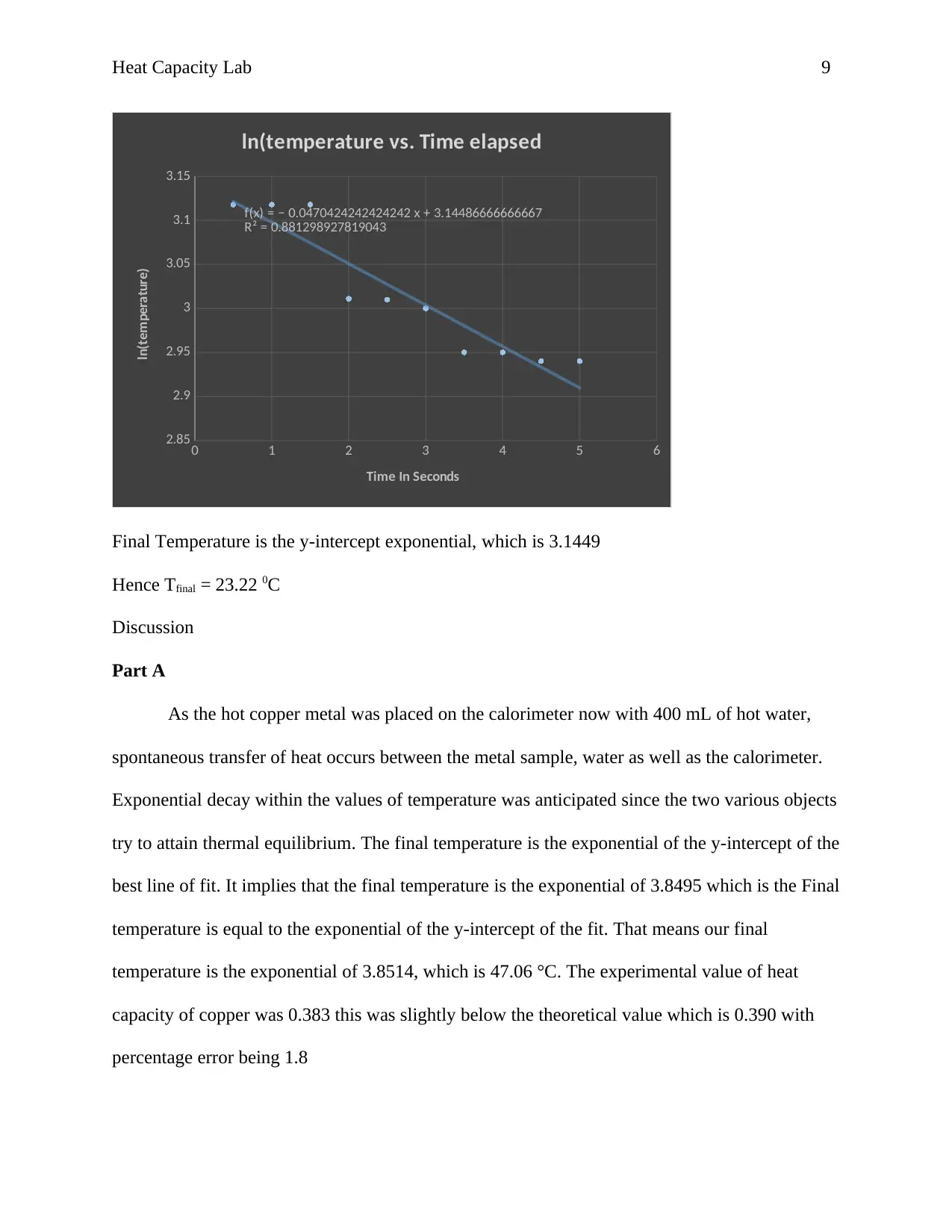
Heat Capacity Lab 9
0 1 2 3 4 5 6
2.85
2.9
2.95
3
3.05
3.1
3.15
f(x) = − 0.0470424242424242 x + 3.14486666666667
R² = 0.881298927819043
ln(temperature vs. Time elapsed
Time In Seconds
ln(temperature)
Final Temperature is the y-intercept exponential, which is 3.1449
Hence Tfinal = 23.22 0C
Discussion
Part A
As the hot copper metal was placed on the calorimeter now with 400 mL of hot water,
spontaneous transfer of heat occurs between the metal sample, water as well as the calorimeter.
Exponential decay within the values of temperature was anticipated since the two various objects
try to attain thermal equilibrium. The final temperature is the exponential of the y-intercept of the
best line of fit. It implies that the final temperature is the exponential of 3.8495 which is the Final
temperature is equal to the exponential of the y-intercept of the fit. That means our final
temperature is the exponential of 3.8514, which is 47.06 °C. The experimental value of heat
capacity of copper was 0.383 this was slightly below the theoretical value which is 0.390 with
percentage error being 1.8

Heat Capacity Lab 10
Part B
The reaction is exothermic since heat is released to the atmosphere. The negative sign shows an
exothermic reaction.
Questions
Calculate the specific heat capacity of copper in J/g.k using equation 1, given the specific heat
capacity of water is 4.184 J/g.K and specific heat capacity of Calorimeter is 60J/K.
Calculation
Heat 𝑙𝑜𝑠𝑡 𝑏𝑦 copper = heat 𝑔𝑎𝑖𝑛𝑒𝑑 𝑏𝑦 𝑤𝑎𝑡𝑒𝑟 + heat 𝑔𝑎𝑖𝑛𝑒𝑑 𝑏𝑦 the 𝑐𝑎𝑙𝑜𝑟𝑖𝑚𝑒𝑡𝑒𝑟
¿ ¿
¿0.385
Parts B Reaction 3

Heat Capacity Lab 11
ΔT1= Tfinal – TInitial= 26.09-22 =4.09
ΔH3= -4.184 x 10-3K/ x 100x10-3 x4.09= -1711.256 x 10-3 KJ/mole
Reaction 4
Tinitial= 22.6 0 C
Tfinal= 23.22
ΔT2=0.62
ΔH4= -4.184 x 10-3K/ x 100x10-3 x 0.62 =- 25.94 x 10-3 Kj/mole
Sources of errors
Errors during the rounding off figures and wrong readings of thermometer due to parallax
error. other possible errors include calorimeter not well insulated, thus allowing heat to escape
through calorimeter. Water volume might have increased while transferring copper metal into the
calorimeter. In addition, the thermometer metal may have touched the copper giving rise to a
faulty reading of temperature.
Conclusion
The experiment was successful as its objectives were achieved even though the values
found were slightly different from the theoretical values. This is because of the various possible
errors as stated above.

Heat Capacity Lab 12
Bibliography
Kotz, J. C., Treichel, P., & Townsend, J. R. (2013). Chemistry and chemical reactivity: Volume
2. Princeton, N.J: Recording for the Blind & Dyslexic.
Signorelli, J. (2014). Chemistry Experiments: For Advanced & Honors Programs. S.l.: Trafford.