Analysis of Heat Transfer in a Fin using Finite Difference Method

This article discusses the analysis of heat transfer in a fin using finite difference method. It explains the three basic mechanisms of heat transfer and the boundary conditions used in the process. The methodology used in the analysis is also explained in detail. The article also includes MATLAB code for the analysis.

Introduction
Heat energy is related to the temperature of matter. For a given material and mass, thermal
energy depend upon the temperature. Due to temperature difference maintain between two
bodies then the heat transfer takes place from higher body to lower body based on law of
thermodynamic. Heat always flow from hot body to cold body. Heat is represented by symbol
Q, and its SI unit is Joule (J). The rate of heat transfer is determined in watts (W), equal to
joules per second.
Hear transfer is energy in transit, which occurs as a result of a temperature gradient or
difference. This temperature difference is thought of as a driving force that causes heat to
flow. Heat transfer occurs by three basic mechanisms or modes:
• Conduction or Diffusion
• Convection
• Radiation
In air cooling system, fins are provided at the outer surface or periphery of engine cylinder to
raise the heat transfer rate. Fins are used to increase the effective area of a surface in an
attempt to maximize heat transfer in both cooling and heating applications. The figure below
shows fin extending from a base. The fin is exposed to an environment at temperature T∞
through convective heat transfer coefficient h. If a constant flow of heat is maintained to the
base then, eventually, the temperature field in the fin can become independent of time. In fin
problems it is this steady-state behaviour that is of interest to the engineer.
That is why the analysis of fin is important. In the present work a fin problem has been
solved. Fin receives a heat of 30 kW/m2 at the bottom surface, while from all other
boundaries it releases heat to the surrounding by convection. Convection heat transfer
coefficient is 300 W/m2-K and ambient temperature is 30°C. Thermal conductivity of the fin
material is 178 W/m-K. From the figure it can be observed that at bottom surface heat flux
boundary condition has been considered which represents that fin is attached to the heated
surface, which can also be seen from the arrow direction, while on other walls convective
boundary condition has been considered which represents that heat losses to the surroundings
by convection.

Two-dimensional heat conduction equation governs the present problem, because in present
case a solid fin has been considered. As we know in solid body heat transfer by conduction
dominates over heat transfer by convection and radiation. So the two-dimensional heat
conduction equation will govern the physical problem,
∂2 T
∂ x2 + ∂2 T
∂ y2 =0
Methodology:
 Finite difference technique has been used to solve the above equation. A uniform grid as
shown in figure below has been used in which all the flow variables are stored at the same
location. MATLAB has been used to simulate the governing equation and boundary
conditions.
 Two-dimensional heat conduction equation first converted to algebraic form using Taylor
series expansion.
 Central scheme for second order derivative has been used to discretize spatial term.

Boundary conditions: At the symmetry boundary condition (B2), insulated boundary
condition is applied, as no heat transfer is taking place from the symmetry wall. At B3, B4,
B6 and B7, convective boundary condition is applied. At B5 constant heat flux boundary
condition is applied.
Types of boundary condition
Dirichlet Condition or constant temperature boundary condition
Values of dependent parameter at the boundaries are defined. In the above shown problem
there is no wall on which we can consider this boundary condition. But it can be represented
as
T = T1 at y = 0 for all x values (0 ≤ x ≤ L)
T = T2 at y = H for all x values (0 ≤ x ≤ L)
Neumann Condition or insulated boundary condition
Derivative of the dependent parameter is given as a constant or as a function of the
independent variable on the boundaries.
In the above problem we can cosider this type boundary condition on the symmetry wall.
∂T
∂ x =0 At x = 0 for all y values (0 ≤ y ≤ L)
Convective type boundary condition
Derivative of the dependent variable is given as a function of the dependent variable on the
boundary.
−k ∂T
∂ x =h ( T−T∞ )
Discretize equation:
a. At B2:
∂T
∂ x =0
Tn(1,j)=T(2,j)
b. At B5:
q=−k ∂ T
∂ x
Tn(i,1)=T(i,2)+(q*dy/k)
c. At B4:

q=k ∂ T
∂ x =−h(T −T ∞)
Tn(nx,j)=(((T_amb*h*dx)/k)+T(nx-1,j))/(1+((h*dx)/k))
d. At B6:
q=k ∂ T
∂ y =−h(T −T ∞)
Tn(i,11)=(((T(i,12)*h*dy)/k)-T(i,12))/(((h*dy)/k)-1)
e. At B3:
q=k ∂ T
∂ x =−h(T −T ∞)
Tn(11,j)=(((T(12,j)*h*dx)/k)-T(12,j))/(((h*dx)/k)-1)
f. At B7
q=k ∂ T
∂ y =−h(T −T ∞)
Tn(i,ny)=(((T_amb*h*dy)/k)+T(i,ny-1))/(1+((h*dy)/k))
g. In D1: Solid:
∂2 T
∂ x2 + ∂2 T
∂ y2 =0
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/
((2/dx^2)+(2/dy^2))
h. In D0: Air:
∂2 T
∂ x2 + ∂2 T
∂ y2 =0
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/
((2/dx^2)+(2/dy^2))

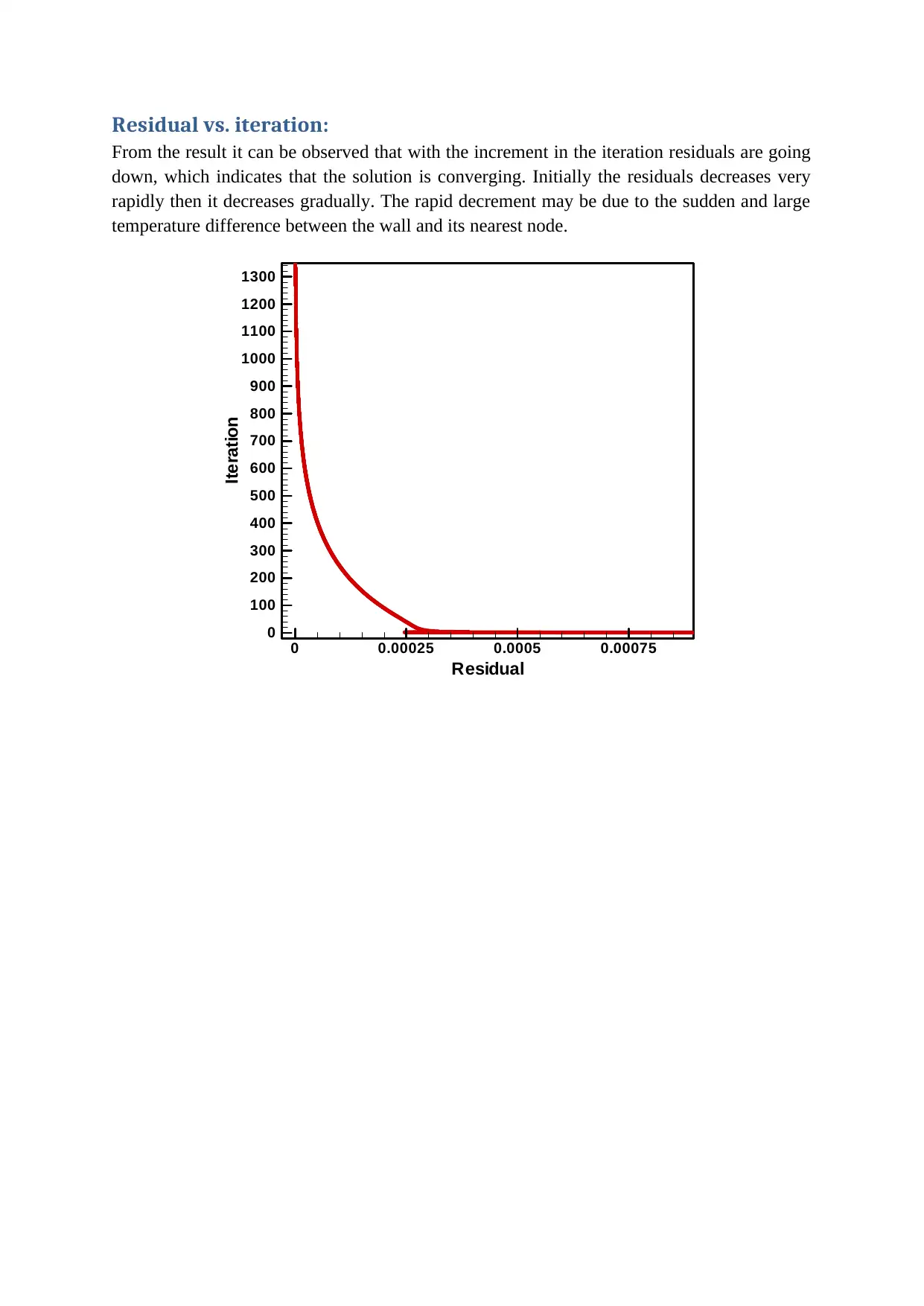
Residual vs. iteration:
From the result it can be observed that with the increment in the iteration residuals are going
down, which indicates that the solution is converging. Initially the residuals decreases very
rapidly then it decreases gradually. The rapid decrement may be due to the sudden and large
temperature difference between the wall and its nearest node.
Residual
Iteration
0 0.00025 0.0005 0.00075
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300

Result and conclusion
Temperature contour:
5 10 15 20 25 30
10
20
30
40
50
60
70
80
90
Temperature along B2:
Symmetry line (B2)
Temperature
0 0.009 0.018 0.027 0.036 0.045
303
303.2
303.4
303.6
303.8
304

MATLAB Code:
clc; clear all;
%Parameters
q=30000; %Heat flux at the base of fin = 30kW/m^2
T_amb=303; %Ambient temperature = 30C
h=300; %Heat transfer coefficient = 300W/m^2-K
k=178; %Fin material thermal conductivity = 178 W/m-K
B2=0.045; %Height of the symmetry surface
B3=0.04; %Height of the vertical right wall
B4=0.005; %Height of the bottom right surface
B5=0.015; %Length of the horizontal bottom surface of the
bottom part
B6=0.01; %Length of the horizontal top surface of the bottom
part
B7=0.005; %
H=0.045; %Full height
L=0.015; %Full length
nx=31;
ny=91;
dx=L/(nx-1);
dy=H/(ny-1);
%Initilisation
for i=1:nx;
for j=1:ny;
T(i,j)=T_amb;
end
end
iter=0;
iter_v=[];
error=10000;
errr_v=[];
tolerance=0.000001;
while error>=tolerance
iter=iter+1;
% iter=1000;
% for itern=1:iter
% itern
%Symmetry wall
for j=1:ny
Tn(1,j)=T(2,j);
end
%Bottom wall (heat flux wall)
for i=2:nx;
Tn(i,1)=T(i,2)+(q*dy/k);
end
%Right side (bottom part)
for j=2:10;
Tn(nx,j)=(((T_amb*h*dx)/k)+T(nx-1,j))/(1+((h*dx)/k));
end
%Horizontal wall (Upper wall of Bottom part of fin)
for i=12:nx;
%Tn(i,11)=T(i,12)-((k/(2*dy*h))*(T(i,12)-T(i,10))); %central
%%T_amb=T(i,12)
%Tn(i,11)=(((T(i,12)*h*dy)/k)+T(i,10))/(((h*dy)/k)+1); %forward
Tn(i,11)=(((T(i,12)*h*dy)/k)-T(i,12))/(((h*dy)/k)-1); %backward
end
%Vertical wall (Upper part of fin)
for j=11:ny;

%Tn(11,j)=T(12,j)-((k/(2*dx*h))*(T(12,j)-T(10,i))); %central
%Tn(11,j)=(((T(12,j)*h*dx)/k)+T(10,j))/(((h*dx)/k)+1);
Tn(11,j)=(((T(12,j)*h*dx)/k)-T(12,j))/(((h*dx)/k)-1);
end
for i=11;
for j =11;
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/...
((2/dx^2)+(2/dy^2));
end
end
%Top verticall wall (upper part of fin)
for i=2:10;
Tn(i,ny)=(((T_amb*h*dy)/k)+T(i,ny-1))/(1+((h*dy)/k));
end
%In the fin horizontal part
for i=2:30;
for j=2:10;
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/...
((2/dx^2)+(2/dy^2));
end
end
%In the fin vertical part
for i=2:10;
for j=11:90;
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/...
((2/dx^2)+(2/dy^2));
end
end
%In the air right vertical wall
for j=12:ny;
Tn(nx,j)=T_amb;
end
%In the air top horizontal wall
for i=12:nx;
Tn(i,ny)=T_amb;
end
%In the air inside the geometry
for i=12:nx-1;
for j=12:ny-1;
Tn(i,j)=(((T(i+1,j)+T(i-1,j))/dx^2)+((T(i,j+1)+T(i,j-1))/dy^2))/...
((2/dx^2)+(2/dy^2));
end
end
error=0;
for i=1:nx;
for j=1:ny;
error=error+abs(Tn(i,j)-T(i,j));
T(i,j)=Tn(i,j);
end
end
To=Tn';
error=error/nx/ny
iter_v=[iter_v,iter];
errr_v=[errr_v,error];
end