Height and Arm Span Statistics Folio: Data Analysis and Report
VerifiedAdded on 2023/06/05
|5
|1252
|275
Practical Assignment
AI Summary
This statistics folio investigates the relationship between height and arm span using various statistical measures. The study includes data collection, calculation of measures of central tendency (mean, median, and mode), and creation of a five-number summary for box plot generation. The analysis aims to determine if taller students have a larger arm span than shorter students. The report includes measurement tables, box plots, and a scatter plot to visualize the correlation between height and arm span. The discussion evaluates the appropriateness of using mean versus median, interprets the scatter plot, and addresses potential experimental design improvements, emphasizing validity and reliability. The conclusion confirms a positive correlation, indicating that taller students generally have larger arm spans, but acknowledges other factors influencing arm span.

Amar Krdea
Introduction:
This investigation includes information about the usage of statistics. Using statistics includes
the ability to analyse and graph numerical data sets. A good occupation that involves
statistics is accounting. Accountants are very skilled and smart when it comes to numbers
and statistics because that’s all their occupation requires. Using the measures of centre is
required to successfully complete this investigation. The measures of centre are median,
mean and mode the means is the average number of a numerical data set. The median is the
middle number in the data set. The mode is the most repeated number in the data set. A
five number summary is than created to make box plots.
Describing sentence
This task aims to calculate if shorter students had a shorter arm span than tall students
Measurement table for the whole class
Height
(cm)
Lengt
h of
feet R
Lengt
h of
feet L
Length
of
forearm
s R
Length
of
forearm
s L
Hand
Span
Left
Hand
span
Right
Arm
Span
171.0 25.5 25.0 30.0 27.0 20.5 20.0 144.0
176.0 26.0 25.5 26.0 27.8 16.5 17.0 140.0
170.5 22.5 22.5 30.0 29.5 17.0 16.0 148.5
157.0 21.0 20.0 25.0 25.0 17.0 17.0 156.0
168.0 24.0 23.0 25.0 25.5 18.5 18.0 168.0
172.0 26.0 25.0 26.0 25.0 23.0 22.5 170.0
174.0 26.0 25.5 23.0 23.0 21.7 22.0 168.0
185.0 29.4 29.0 26.5 26.5 23.5 24.0 185.0
151.0 22.0 22.0 24.0 24.0 19.5 19.5 149.0
180.0 27.0 27.0 27.0 27.0 22.0 22.0 184.0
173.0 25.5 25.5 25.0 25.0 20.5 20.5 169.0
165.0 25.0 25.0 24.0 24.0 18.0 18.0 165.0
177.0 26.0 26.0 27.0 27.0 23.0 22.0 184.0
183.0 28.5 28.5 30.0 30.0 24.0 24.0 187.0
167.0 25.0 25.0 24.0 24.0 21.0 21.0 180.0
177.0 27.0 27.0 25.0 25.0 23.0 23.0 179.0
182.0 28.0 28.0 26.0 26.0 23.0 23.0 185.0
160.0 24.5 24.5 24.5 24.5 17.5 17.9 153.0
164.0 24.0 24.0 24.0 24.0 19.5 19.3 160.0
167.0 25.5 25.5 25.5 25.5 19.0 19.0 170.0
164.0 24.0 24.0 24.0 24.0 20.4 20.5 162.0
Statistic
s Folio
Introduction:
This investigation includes information about the usage of statistics. Using statistics includes
the ability to analyse and graph numerical data sets. A good occupation that involves
statistics is accounting. Accountants are very skilled and smart when it comes to numbers
and statistics because that’s all their occupation requires. Using the measures of centre is
required to successfully complete this investigation. The measures of centre are median,
mean and mode the means is the average number of a numerical data set. The median is the
middle number in the data set. The mode is the most repeated number in the data set. A
five number summary is than created to make box plots.
Describing sentence
This task aims to calculate if shorter students had a shorter arm span than tall students
Measurement table for the whole class
Height
(cm)
Lengt
h of
feet R
Lengt
h of
feet L
Length
of
forearm
s R
Length
of
forearm
s L
Hand
Span
Left
Hand
span
Right
Arm
Span
171.0 25.5 25.0 30.0 27.0 20.5 20.0 144.0
176.0 26.0 25.5 26.0 27.8 16.5 17.0 140.0
170.5 22.5 22.5 30.0 29.5 17.0 16.0 148.5
157.0 21.0 20.0 25.0 25.0 17.0 17.0 156.0
168.0 24.0 23.0 25.0 25.5 18.5 18.0 168.0
172.0 26.0 25.0 26.0 25.0 23.0 22.5 170.0
174.0 26.0 25.5 23.0 23.0 21.7 22.0 168.0
185.0 29.4 29.0 26.5 26.5 23.5 24.0 185.0
151.0 22.0 22.0 24.0 24.0 19.5 19.5 149.0
180.0 27.0 27.0 27.0 27.0 22.0 22.0 184.0
173.0 25.5 25.5 25.0 25.0 20.5 20.5 169.0
165.0 25.0 25.0 24.0 24.0 18.0 18.0 165.0
177.0 26.0 26.0 27.0 27.0 23.0 22.0 184.0
183.0 28.5 28.5 30.0 30.0 24.0 24.0 187.0
167.0 25.0 25.0 24.0 24.0 21.0 21.0 180.0
177.0 27.0 27.0 25.0 25.0 23.0 23.0 179.0
182.0 28.0 28.0 26.0 26.0 23.0 23.0 185.0
160.0 24.5 24.5 24.5 24.5 17.5 17.9 153.0
164.0 24.0 24.0 24.0 24.0 19.5 19.3 160.0
167.0 25.5 25.5 25.5 25.5 19.0 19.0 170.0
164.0 24.0 24.0 24.0 24.0 20.4 20.5 162.0
Statistic
s Folio
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Amar Krdea
166.0 28.0 26.5 26.0 24.0 21.0 20.5 168.0
176.0 26.5 26.5 27.0 27.0 21.5 21.0 176.0
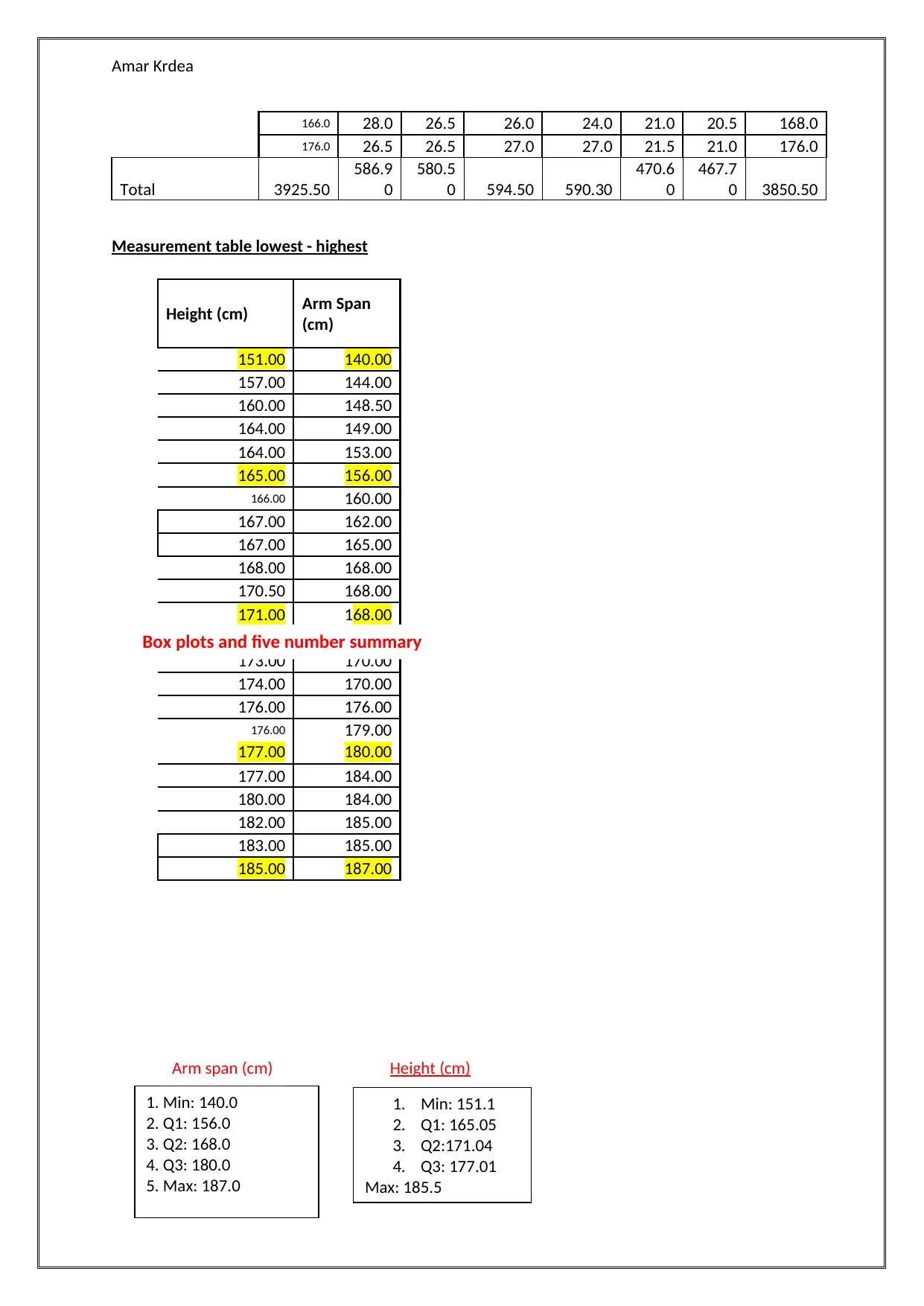
Total 3925.50
586.9
0
580.5
0 594.50 590.30
470.6
0
467.7
0 3850.50
Measurement table lowest - highest
1. Min: 151.1
2. Q1: 165.05
3. Q2:171.04
4. Q3: 177.01
Max: 185.5
1. Min: 140.0
2. Q1: 156.0
3. Q2: 168.0
4. Q3: 180.0
5. Max: 187.0
Height (cm)Arm span (cm)
Height (cm) Arm Span
(cm)
151.00 140.00
157.00 144.00
160.00 148.50
164.00 149.00
164.00 153.00
165.00 156.00
166.00 160.00
167.00 162.00
167.00 165.00
168.00 168.00
170.50 168.00
171.00 168.00
172.00 169.00
173.00 170.00
174.00 170.00
176.00 176.00
176.00 179.00
177.00 180.00
177.00 184.00
180.00 184.00
182.00 185.00
183.00 185.00
185.00 187.00
Box plots and five number summary
166.0 28.0 26.5 26.0 24.0 21.0 20.5 168.0
176.0 26.5 26.5 27.0 27.0 21.5 21.0 176.0
Total 3925.50
586.9
0
580.5
0 594.50 590.30
470.6
0
467.7
0 3850.50
Measurement table lowest - highest
1. Min: 151.1
2. Q1: 165.05
3. Q2:171.04
4. Q3: 177.01
Max: 185.5
1. Min: 140.0
2. Q1: 156.0
3. Q2: 168.0
4. Q3: 180.0
5. Max: 187.0
Height (cm)Arm span (cm)
Height (cm) Arm Span
(cm)
151.00 140.00
157.00 144.00
160.00 148.50
164.00 149.00
164.00 153.00
165.00 156.00
166.00 160.00
167.00 162.00
167.00 165.00
168.00 168.00
170.50 168.00
171.00 168.00
172.00 169.00
173.00 170.00
174.00 170.00
176.00 176.00
176.00 179.00
177.00 180.00
177.00 184.00
180.00 184.00
182.00 185.00
183.00 185.00
185.00 187.00
Box plots and five number summary

Amar Krdea
1. Height and arm span graph
150.0 155.0 160.0 165.0 170.0 175.0 180.0 185.0 190.0
130.0
140.0
150.0
160.0
170.0
180.0
190.0
R² = 0.387900060089257
Height and Arm span graph
Height (cm)
Arm span (cm)
2. Handwritten work
5 number summary (Arm span)5 number summary (Height)
Mean, Mode, Median (Height) Mean, Mode, Median (Arm span)
The whisker plots and box show a
symmetrical correlation as well as a
negatively skewed correlation. The
Height is symmetrically correlated. The
arm span box plots and whisker plots
show a more negative correlation.
1. Height and arm span graph
150.0 155.0 160.0 165.0 170.0 175.0 180.0 185.0 190.0
130.0
140.0
150.0
160.0
170.0
180.0
190.0
R² = 0.387900060089257
Height and Arm span graph
Height (cm)
Arm span (cm)
2. Handwritten work
5 number summary (Arm span)5 number summary (Height)
Mean, Mode, Median (Height) Mean, Mode, Median (Arm span)
The whisker plots and box show a
symmetrical correlation as well as a
negatively skewed correlation. The
Height is symmetrically correlated. The
arm span box plots and whisker plots
show a more negative correlation.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Amar Krdea
Discussion.
The average of the dataset is best represented by mean when the underlying dataset is not
skewed. This is because owing to presence of extreme values, the mean value may be distorted
and thus in such cases median could be more useful. The boxplot highlights the presence of
negative skew owing to which median might be preferable to mean as an indicator of average.
From the scatter plot of height and arm span, it is apparent that a positive correlation exists
between the variables. This implies that when height increases, the arm span also tends to
increase. Another aspect related to the strength of the correlation which would depend on the
position of scatter points about the line of best fit. It is apparent that there are three outliers in
the given data and hence the overall strength of the relationship between the given variables
seems moderate. The R2 value also indicates the same since only 38.79% of the changes in arm
span are explained by corresponding changes in the height. This clearly implies that there are
other factors responsible for arm span besides height and those cannot be ignored.
One clear advantage of an experimental design is the high accuracy provided there are no
human errors in recording and measurement. Suitable measures must be undertaken in order to
avoid these errors by ensuring that the observations are cross checked and also the underlying
equipment used to perform measurements are error free. In this regards, two properties are
imperative i.e. validity and reliability. Reliability refers to the ability of a measuring machine to
provide the same reading of height or arm span for a given student when the measurement
process is repeated. Validity refers to the ability of the measuring devices to provide the correct
measurements.
.
Conclusion.
In conclusion to this task, the statement “taller students had a larger arm span than the smaller
students” is correct and this can be seen with the scatter plot. The data in the scatter plot has a
positive correlation meaning that if a student was at a height of 150cm their arm span would be
+150cm.
Assessment Rubric
A B C D E
Discussion.
The average of the dataset is best represented by mean when the underlying dataset is not
skewed. This is because owing to presence of extreme values, the mean value may be distorted
and thus in such cases median could be more useful. The boxplot highlights the presence of
negative skew owing to which median might be preferable to mean as an indicator of average.
From the scatter plot of height and arm span, it is apparent that a positive correlation exists
between the variables. This implies that when height increases, the arm span also tends to
increase. Another aspect related to the strength of the correlation which would depend on the
position of scatter points about the line of best fit. It is apparent that there are three outliers in
the given data and hence the overall strength of the relationship between the given variables
seems moderate. The R2 value also indicates the same since only 38.79% of the changes in arm
span are explained by corresponding changes in the height. This clearly implies that there are
other factors responsible for arm span besides height and those cannot be ignored.
One clear advantage of an experimental design is the high accuracy provided there are no
human errors in recording and measurement. Suitable measures must be undertaken in order to
avoid these errors by ensuring that the observations are cross checked and also the underlying
equipment used to perform measurements are error free. In this regards, two properties are
imperative i.e. validity and reliability. Reliability refers to the ability of a measuring machine to
provide the same reading of height or arm span for a given student when the measurement
process is repeated. Validity refers to the ability of the measuring devices to provide the correct
measurements.
.
Conclusion.
In conclusion to this task, the statement “taller students had a larger arm span than the smaller
students” is correct and this can be seen with the scatter plot. The data in the scatter plot has a
positive correlation meaning that if a student was at a height of 150cm their arm span would be
+150cm.
Assessment Rubric
A B C D E
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Amar Krdea
Compare data
sets by
referring to the
shapes of the
various data
displays
Students can
highly
effectively compar
e data sets by
referring to the
shapes of the
various data
displays
Students
proficiently compar
e data sets by
referring to the
shapes of the
various data
displays
Students
appropriately compa
re data sets by
referring to the
shapes of the
various data displays
Students
partially compar
e data sets by
referring to the
shapes of the
various data
displays
Students have
limited ability
to compare
data sets by
referring to the
shapes of the
various data
displays
Describe
statistical
relationships
between two
continuous
variables
Students highly
effectively describ
e statistical
relationships
between two
continuous
variables
Students
proficiently describ
e statistical
relationships
between two
continuous
variables
Students
appropriately describ
e statistical
relationships
between two
continuous variables
Students
partially describ
e statistical
relationships
between two
continuous
variables
Students have
limited ability
to describe
statistical
relationships
between two
continuous
variables
Evaluates
statistical
reports
Students highly
effectively evaluat
e statistical
reports
Students
proficiently evaluat
e statistical reports
Students
appropriately evaluat
e statistical reports
Students
partially evaluat
e statistical
reports
Students have
limited ability to
evaluate
statistical
reports
Calculate
quartiles and
inter-quartile
ranges
Students highly
effectively calcula
te quartiles and
inter-quartile
ranges
Students
proficiently calcula
te quartiles and
inter-quartile
ranges
Students
appropriately calcula
te quartiles and
inter-quartile ranges
Students
partially calculat
e quartiles and
inter-quartile
ranges
Students have
limited ability
to calculate
quartiles and
inter-quartile
ranges
Compare data
sets by
referring to the
shapes of the
various data
displays
Students can
highly
effectively compar
e data sets by
referring to the
shapes of the
various data
displays
Students
proficiently compar
e data sets by
referring to the
shapes of the
various data
displays
Students
appropriately compa
re data sets by
referring to the
shapes of the
various data displays
Students
partially compar
e data sets by
referring to the
shapes of the
various data
displays
Students have
limited ability
to compare
data sets by
referring to the
shapes of the
various data
displays
Describe
statistical
relationships
between two
continuous
variables
Students highly
effectively describ
e statistical
relationships
between two
continuous
variables
Students
proficiently describ
e statistical
relationships
between two
continuous
variables
Students
appropriately describ
e statistical
relationships
between two
continuous variables
Students
partially describ
e statistical
relationships
between two
continuous
variables
Students have
limited ability
to describe
statistical
relationships
between two
continuous
variables
Evaluates
statistical
reports
Students highly
effectively evaluat
e statistical
reports
Students
proficiently evaluat
e statistical reports
Students
appropriately evaluat
e statistical reports
Students
partially evaluat
e statistical
reports
Students have
limited ability to
evaluate
statistical
reports
Calculate
quartiles and
inter-quartile
ranges
Students highly
effectively calcula
te quartiles and
inter-quartile
ranges
Students
proficiently calcula
te quartiles and
inter-quartile
ranges
Students
appropriately calcula
te quartiles and
inter-quartile ranges
Students
partially calculat
e quartiles and
inter-quartile
ranges
Students have
limited ability
to calculate
quartiles and
inter-quartile
ranges
1 out of 5
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.