Hierarchical Portfolio Search: Prismata’s Robust AI Architecture for Games with Large Search Spaces
VerifiedAdded on 2023/06/15
|7
|6568
|53
AI Summary
This paper introduces Hierarchical Portfolio Search, a novel method for performing hierarchical search using a portfolio of algorithms to reduce the search space while maintaining strong action candidates. It discusses its role in creating a strong and robust AI system for the commercial strategy game Prismata by Lunarch Studios. The paper also talks about the challenges of creating AI systems for modern video games and the design goals that should be considered. It includes an overview of Prismata, its game properties, and the AI challenges it presents.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Hierarchical Portfolio Search: Prismata’s Robust
AI Architecture for Games with Large Search Spaces
David Churchill and Michael Buro
University of Alberta, Edmonton, T6G 2E8, Canada
Email: dave.churchill@gmail.com,mburo@ualberta.ca
Abstract
Online strategy video games offer several unique challenges
to the field of AI research. Due to their large state and action
spaces, existing search algorithms have difficulties in mak-
ing strategically strong decisions. Additionally, the nature of
competitive on-line video games adds the requirement that
game designers be able to tweak game properties regularly
when strategic imbalances are found. This means that an AI
system for a game like this needs to be robust to such changes
and less reliant on expert knowledge. This paper makes two
main contributions to advancing the state of the art for AI in
modern strategy video games which have large state and ac-
tion spaces. The first is a novel method for performing hier-
archical search using a portfolio of algorithms to reduce the
search space while maintaining strong action candidates. The
second contribution is an overall AI architecture for strategy
video games using this portfolio search method. The proposed
methods are used as the AI system for Prismata, an online
turn-based strategy game by Lunarch Studios. This system
is evaluated using three experiments: on-line play vs. human
players, off-line AI tournaments to test the relative strengths of
the AI bots, and a survey to determine user satisfaction of the
system so far. Our result show that this system achieves a skill
level in the top 25% of human players on the ranked ladder,
can be modified quickly to create different difficulty settings,
is robust to changes in game unit properties, and creates an
overall AI experience which is user rated more enjoyable than
those currently found in similar video games.
Introduction
Creating AI systems for modern (video) games is compli-
cated by their decision complexity, players expecting to be
tutored about how to play and being challenged and enter-
tained as they become better players, and the high cost of
maintaining software in the presence of frequent game ad-
justments such as balancing or adding new game features.
AI programmers are therefore looking for ways to automate
decision making beyond relying solely on manually tuned be-
havior, creating AI systems that are more robust with respect
to game changes, and also making them better adjust to hu-
man players’ preferences and playing strength.
AI successes in abstract games such as Checkers (Scha-
effer et al. 1996), Chess, Go, and recently heads-up limit
Poker (Bowling et al. 2015) have taught us the great value of
Copyright c 2015, Association for the Advancement of Artificial
Intelligence (www.aaai.org). All rights reserved.
fast look-ahead search and vast pre-computed databases stor-
ing perfect state evaluations or moves. Applying these tech-
niques to complex video games requires simplifications in
form of state and action abstractions because of huge search
spaces which can’t be handled by classic search methods
such as Alpha-Beta search in real-time. An approach that
has been focused on in recent years in the RTS game AI re-
search community is to reduce branching factors by using
scripted move generators and use those in look-ahead search
procedures to improve real-time decision quality (Churchill
and Buro 2013), obtaining encouraging initial results. In this
paper we introduce a generalized search procedure we call
Hierarchical Portfolio Search and discuss its role in creating
a strong and robust AI system for the commercial strategy
game Prismata by Lunarch Studios (LunarchStudios 2015).
After discussing specific game AI challenges, we present
our new generic search procedure, introduce Prismata, and
show game strength evaluations and the results of an AI user
survey. Ideas on future research conclude the paper.
AI Design Goals
Typically, academic literature on game AI is focused mostly
on algorithms which improve the strategic strength of game-
playing agents. For a retail game however, the goal is not nec-
essarily to maximize the playing strength of the AI system,
but instead to provide for the best experience for its users.
When making game AI systems, other design goals should
also be considered:
• New Player Tutorial. Because new games may have fairly
steep learning curves, an AI system should be a tool which
aids new players in learning the game rules and strategies.
It should also offer different difficulty settings so that play-
ers have a gradual introduction rather than being placed
immediately at the highest difficulty.
• Experienced Player Training. Experienced and compet-
itive players often want to practice without “giving away”
strategies to other players. The hardest AI difficulty should
be able to put up enough fight so that players can practice
these strategies with some resistance.
• Single Player Replayability. Single-player missions in
video games are usually implemented as scripted se-
quences of events that play out the same way every time,
allowing a player memorize strategies in order to defeat
them. In order to add replay value the AI system should
Proceedings, The Eleventh AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE-15)
16
AI Architecture for Games with Large Search Spaces
David Churchill and Michael Buro
University of Alberta, Edmonton, T6G 2E8, Canada
Email: dave.churchill@gmail.com,mburo@ualberta.ca
Abstract
Online strategy video games offer several unique challenges
to the field of AI research. Due to their large state and action
spaces, existing search algorithms have difficulties in mak-
ing strategically strong decisions. Additionally, the nature of
competitive on-line video games adds the requirement that
game designers be able to tweak game properties regularly
when strategic imbalances are found. This means that an AI
system for a game like this needs to be robust to such changes
and less reliant on expert knowledge. This paper makes two
main contributions to advancing the state of the art for AI in
modern strategy video games which have large state and ac-
tion spaces. The first is a novel method for performing hier-
archical search using a portfolio of algorithms to reduce the
search space while maintaining strong action candidates. The
second contribution is an overall AI architecture for strategy
video games using this portfolio search method. The proposed
methods are used as the AI system for Prismata, an online
turn-based strategy game by Lunarch Studios. This system
is evaluated using three experiments: on-line play vs. human
players, off-line AI tournaments to test the relative strengths of
the AI bots, and a survey to determine user satisfaction of the
system so far. Our result show that this system achieves a skill
level in the top 25% of human players on the ranked ladder,
can be modified quickly to create different difficulty settings,
is robust to changes in game unit properties, and creates an
overall AI experience which is user rated more enjoyable than
those currently found in similar video games.
Introduction
Creating AI systems for modern (video) games is compli-
cated by their decision complexity, players expecting to be
tutored about how to play and being challenged and enter-
tained as they become better players, and the high cost of
maintaining software in the presence of frequent game ad-
justments such as balancing or adding new game features.
AI programmers are therefore looking for ways to automate
decision making beyond relying solely on manually tuned be-
havior, creating AI systems that are more robust with respect
to game changes, and also making them better adjust to hu-
man players’ preferences and playing strength.
AI successes in abstract games such as Checkers (Scha-
effer et al. 1996), Chess, Go, and recently heads-up limit
Poker (Bowling et al. 2015) have taught us the great value of
Copyright c 2015, Association for the Advancement of Artificial
Intelligence (www.aaai.org). All rights reserved.
fast look-ahead search and vast pre-computed databases stor-
ing perfect state evaluations or moves. Applying these tech-
niques to complex video games requires simplifications in
form of state and action abstractions because of huge search
spaces which can’t be handled by classic search methods
such as Alpha-Beta search in real-time. An approach that
has been focused on in recent years in the RTS game AI re-
search community is to reduce branching factors by using
scripted move generators and use those in look-ahead search
procedures to improve real-time decision quality (Churchill
and Buro 2013), obtaining encouraging initial results. In this
paper we introduce a generalized search procedure we call
Hierarchical Portfolio Search and discuss its role in creating
a strong and robust AI system for the commercial strategy
game Prismata by Lunarch Studios (LunarchStudios 2015).
After discussing specific game AI challenges, we present
our new generic search procedure, introduce Prismata, and
show game strength evaluations and the results of an AI user
survey. Ideas on future research conclude the paper.
AI Design Goals
Typically, academic literature on game AI is focused mostly
on algorithms which improve the strategic strength of game-
playing agents. For a retail game however, the goal is not nec-
essarily to maximize the playing strength of the AI system,
but instead to provide for the best experience for its users.
When making game AI systems, other design goals should
also be considered:
• New Player Tutorial. Because new games may have fairly
steep learning curves, an AI system should be a tool which
aids new players in learning the game rules and strategies.
It should also offer different difficulty settings so that play-
ers have a gradual introduction rather than being placed
immediately at the highest difficulty.
• Experienced Player Training. Experienced and compet-
itive players often want to practice without “giving away”
strategies to other players. The hardest AI difficulty should
be able to put up enough fight so that players can practice
these strategies with some resistance.
• Single Player Replayability. Single-player missions in
video games are usually implemented as scripted se-
quences of events that play out the same way every time,
allowing a player memorize strategies in order to defeat
them. In order to add replay value the AI system should
Proceedings, The Eleventh AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE-15)
16
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

be more dynamic, ensuring the player doesn’t fight against
the same tactics every time they play.
• Robust to Change. Unlike a game like Chess, the game
objects in modern games may have properties that need
to be tweaked over time for strategic balancing. If the AI
system were based on hard-coded scripts it could require
maintenance every time an object was updated, costing
valuable time for programmers.
Hierarchical Portfolio Search
The algorithm we propose for making decisions in large
search spaces is called Hierarchical Portfolio Search (HPS).
It is based off previous work in the field of real-time strat-
egy game AI, namely the portfolio greedy search algorithm
(Churchill and Buro 2013), which used a greedy hill climb-
ing algorithm to assign scripted actions to individual units.
The key idea of portfolio based search methods is that in-
stead of iterating over all possible actions for a given state
we use a portfolio of algorithms to generate a much smaller,
yet (hopefully) intelligent set of actions. This method is par-
ticularly useful in scenarios where a player’s decision can
be decomposed into many individual actions, such as real-
time strategy games like StarCraft or collectible card games
like Hearthstone or Magic: the Gathering. Typically these
decompositions are inspired by tactical components of the
game such as economy, defense, and offense.
We extend the previous methods by creating HPS: a
bottom-up, two level hierarchical search system inspired by
military hierarchical command structure (Wilson 2012). At
the bottom layer there is a portfolio of algorithms which gen-
erate multiple suggestions for each of several tactically de-
composed areas of the game turn. At the top layer, all pos-
sible combinations of these suggestions are iterated over by
a high-level search technique (such as MiniMax or Monte-
Carlo tree search) which makes the final decision on which
move to perform. While it is possible that this abstraction
may not generate the strategically optimal move for a given
turn, there may have been so many possible actions for that
turn that finding the optimal move was intractable.
Components of HPS
Let us now define the components of the HPS system:
State s containing all relevant game state information
Move m = ha1, . . . , ak i , a sequence of Actions ai
Player function p [m = p(s)]
• Input state s
• Performs Move decision logic
• Returns move m generated by p at state s
Game function g [s0 = g(s, p1, p2)]
• Initial state s and Players p1, p2
• Performs game rules / logic
• Returns final game state s0 (win, lose, or draw)
These are the basic components needed for most AI sys-
tems which work on abstract games. In order to implement
Hierarchical Portfolio Search we will need to add two more
components to this list. The first is a Partial Player function,
Algorithm 1 HPS using NegaMax
1: procedure HPS(State s, Portfolio p)
2: return NegaMax(s, p, maxDepth)
3:
4: procedure GenerateChildren(State s, Portfolio p)
5: m[] ← ∅
6: for all move phases f in s do
7: m[f] ← ∅
8: for PartialPlayers ppin p[f ]do
9: m[f ].add(pp(s))
10: moves[] ← crossProduct(m[f ]: move phase f )
11: return ApplyMovesToState(moves,s)
12:
13: procedure NegaMax(State s, Portfolio p, Depth d)
14: if (D == 0) or s.isTerminal() then
15: Player e ← playout player for state evaluation
16: return Game(s, e, e).eval()
17: children[] ← GenerateChildren(s, p)
18: bestVal ← −∞
19: for all c in children do
20: val ← −NegaMax(c, p, d − 1)
21: bestVal ← max(bestVal, val)
22: return bestVal
which like a Player function computes move decision logic,
but a Partial Player computes only a partial move for a turn.
An example of a partial move would be in a real-time strategy
game where a player could have an army composed of many
unit types: a Partial Player function would then compute the
actions of a single unit type.
PartialPlayer function pp [m = pp(s)]
• Input state s
• Performs decision logic for a subset of a turn
• Returns partial Move m to perform at state s
The final component of HPS is the portfolio itself which is a
collection of Partial Player functions:
Portfolio P = hpp1, pp2, ..., ppn i
The internal structure of the Portfolio will depend on the
game being played. However, it is advised that partial play-
ers be grouped by tactical category or game phase. Iterating
over all moves produced by partial players in the portfolio can
then be performed by the GenerateChildren procedure in Al-
gorithm 1. Once a portfolio is created we can then apply any
high-level search algorithm (such as Monte-Carlo tree search
or MiniMax) to iterate over all legal move combinations cre-
ated by the partial players contained within.
State Evaluation
Even with the aid of HPS, games with many turns produce
deep game trees which are unfeasible to search completely.
We must therefore use a heuristic evaluation of a game state
for use in leaf nodes of the heuristic search. It was shown in
(Churchill, Saffidine, and Buro 2012) that for complex strat-
egy games, formula-based evaluation functions can be used
to some success, but are outperformed by evaluations using
17
the same tactics every time they play.
• Robust to Change. Unlike a game like Chess, the game
objects in modern games may have properties that need
to be tweaked over time for strategic balancing. If the AI
system were based on hard-coded scripts it could require
maintenance every time an object was updated, costing
valuable time for programmers.
Hierarchical Portfolio Search
The algorithm we propose for making decisions in large
search spaces is called Hierarchical Portfolio Search (HPS).
It is based off previous work in the field of real-time strat-
egy game AI, namely the portfolio greedy search algorithm
(Churchill and Buro 2013), which used a greedy hill climb-
ing algorithm to assign scripted actions to individual units.
The key idea of portfolio based search methods is that in-
stead of iterating over all possible actions for a given state
we use a portfolio of algorithms to generate a much smaller,
yet (hopefully) intelligent set of actions. This method is par-
ticularly useful in scenarios where a player’s decision can
be decomposed into many individual actions, such as real-
time strategy games like StarCraft or collectible card games
like Hearthstone or Magic: the Gathering. Typically these
decompositions are inspired by tactical components of the
game such as economy, defense, and offense.
We extend the previous methods by creating HPS: a
bottom-up, two level hierarchical search system inspired by
military hierarchical command structure (Wilson 2012). At
the bottom layer there is a portfolio of algorithms which gen-
erate multiple suggestions for each of several tactically de-
composed areas of the game turn. At the top layer, all pos-
sible combinations of these suggestions are iterated over by
a high-level search technique (such as MiniMax or Monte-
Carlo tree search) which makes the final decision on which
move to perform. While it is possible that this abstraction
may not generate the strategically optimal move for a given
turn, there may have been so many possible actions for that
turn that finding the optimal move was intractable.
Components of HPS
Let us now define the components of the HPS system:
State s containing all relevant game state information
Move m = ha1, . . . , ak i , a sequence of Actions ai
Player function p [m = p(s)]
• Input state s
• Performs Move decision logic
• Returns move m generated by p at state s
Game function g [s0 = g(s, p1, p2)]
• Initial state s and Players p1, p2
• Performs game rules / logic
• Returns final game state s0 (win, lose, or draw)
These are the basic components needed for most AI sys-
tems which work on abstract games. In order to implement
Hierarchical Portfolio Search we will need to add two more
components to this list. The first is a Partial Player function,
Algorithm 1 HPS using NegaMax
1: procedure HPS(State s, Portfolio p)
2: return NegaMax(s, p, maxDepth)
3:
4: procedure GenerateChildren(State s, Portfolio p)
5: m[] ← ∅
6: for all move phases f in s do
7: m[f] ← ∅
8: for PartialPlayers ppin p[f ]do
9: m[f ].add(pp(s))
10: moves[] ← crossProduct(m[f ]: move phase f )
11: return ApplyMovesToState(moves,s)
12:
13: procedure NegaMax(State s, Portfolio p, Depth d)
14: if (D == 0) or s.isTerminal() then
15: Player e ← playout player for state evaluation
16: return Game(s, e, e).eval()
17: children[] ← GenerateChildren(s, p)
18: bestVal ← −∞
19: for all c in children do
20: val ← −NegaMax(c, p, d − 1)
21: bestVal ← max(bestVal, val)
22: return bestVal
which like a Player function computes move decision logic,
but a Partial Player computes only a partial move for a turn.
An example of a partial move would be in a real-time strategy
game where a player could have an army composed of many
unit types: a Partial Player function would then compute the
actions of a single unit type.
PartialPlayer function pp [m = pp(s)]
• Input state s
• Performs decision logic for a subset of a turn
• Returns partial Move m to perform at state s
The final component of HPS is the portfolio itself which is a
collection of Partial Player functions:
Portfolio P = hpp1, pp2, ..., ppn i
The internal structure of the Portfolio will depend on the
game being played. However, it is advised that partial play-
ers be grouped by tactical category or game phase. Iterating
over all moves produced by partial players in the portfolio can
then be performed by the GenerateChildren procedure in Al-
gorithm 1. Once a portfolio is created we can then apply any
high-level search algorithm (such as Monte-Carlo tree search
or MiniMax) to iterate over all legal move combinations cre-
ated by the partial players contained within.
State Evaluation
Even with the aid of HPS, games with many turns produce
deep game trees which are unfeasible to search completely.
We must therefore use a heuristic evaluation of a game state
for use in leaf nodes of the heuristic search. It was shown in
(Churchill, Saffidine, and Buro 2012) that for complex strat-
egy games, formula-based evaluation functions can be used
to some success, but are outperformed by evaluations using
17

symmetric game playouts. The concept is that even if the
policy used in a playout is not optimal, if both players fol-
low this policy to the end of the game from a given state the
winner probably had an advantage in the original state. The
Game function is used to perform this playout for evaluation.
Finally, an example of HPS using NegaMax as the top-
level search algorithm and Game playouts as the heuristic
evaluation method can be seen in Algorithm 1.
Prismata
Prismata is a strategy game developed by Lunarch Studios
which combines “concepts from real-time strategy games,
collectible card games, and table-top strategy games” (Lu-
narchStudios 2015). Prismata has the following game prop-
erties:
1. Two player - While Prismata does have single player puz-
zle and campaign modes, this paper will focus on the more
popular and competitive 1 vs. 1 form of Prismata
2. Alternating Move - Players take turns performing moves
like in Chess. However, turns may consists of multiple
actions taken by the same player (such as buying units or
attacking). The turn is over when the active player declares
no additional actions and passes, or a time limit is reached
3. Zero Sum - The outcome of a game of Prismata is a win,
loss or a draw (stalemate), with a winner being declared if
they have destroyed all enemy units.
4. Perfect Information - All players in Prismata have ac-
cess to all of the game’s information. There are no decks,
hands, or fog of war to keep information secret from your
opponent like in some other strategy games.
5. Deterministic - At the beginning of a game, a random set
of 5 or 8 units (depending on the game type) is added to the
base pool of purchasable units. After this randomization
of the initial state, all game rules are deterministic.
Game Description
In Prismata, each player controls a number of units and has a
set of resources which are generated by the units they control.
These resources can then be consumed to purchase additional
units which can eventually create enough attack power to de-
stroy enemy units. The main elements and rules of the game
are as follows:
1. Units: Each player in Prismata controls a number of units,
similar to a real-time strategy game. Players build up an
army by purchasing additional units throughout the game
in order to attack the enemy player and defend from in-
coming attacks. There are dozens of unique unit types in
the game, with each player being able to purchase multi-
ple instances of each unit type, similar to how a player in
a real-time strategy game can have multiple instances of
unit such as a tank or a marine. Each unit type in Prismata
has a number of properties such as initial hit points, life
span, whether or not it can block, etc.
2. Abilities: Each unit type has a unique set of abilities which
allow it to perform specific actions such as: produce re-
sources, increase attack, defend, or kill / create other units.
The most basic and important unit of any Prismata game
is the Drone, whose ability can be used by the player to
produce one gold resource. Unit abilities can only be ac-
tivated once per turn during the action phase.
3. Resources: There are 6 resource types in Prismata: gold,
energy, red, blue, green, and attack. The gold and green
resource types accumulate from turn to turn, while energy,
red, and blue are depleted at the end of a turn. Attack is a
special resource and is explained in the next section. Play-
ers may choose to consume resources in order to purchase
additional units or activate unit abilities.
4. Combat: The goal of Prismata is to destroy all enemy
units. Combat in Prismata consists of two main steps: At-
tacking and Blocking. Unlike most strategy games, units
do not specifically attack other units, instead a unit gener-
ates an amount of attack which is summed with all other
attacking units into a single attack amount. Any amount of
Attack generated by units during a player’s turn must be
assigned by the enemy to their defensive units (blocked)
during the Defense phase of their next turn. When a de-
fensive player chooses a blocker with h health to defend
against a incoming attack: if a ≥ h the blocking unit is
destroyed and the process repeats witha−h remaining at-
tack. If a = 0or a < hthe blocking unit lives and the de-
fense phase is complete. If a player generates more attack
than their opponent can block, then all enemy blockers are
destroyed and the attacking player enters the Breach phase
where remaining damage is assigned to enemy units of the
attacker’s choosing.
AI Challenges
Prismata is a challenging game to write an AI for, mainly
due to its large state and action spaces which create unique
challenges for even state-of-the-art search algorithms.
State Space The state space of a game (how many board
positions are possible) is often used as an intuitive measure
of game complexity. In Prismata, we can calculate a rough
estimate of the state space as follows. In a typical Base +
8 game players have access to 11 base units and 8 random
units, for a total of 19 units per player, or 38 in total. If we
give a conservative average supply limit of 10 per unit per
player, then the number of possible combinations of units
on the board at one time in Prismata is approximately 1040.
We then have to consider that each unit can have different
properties: can be used or unused, have different amounts of
hit points, stamina, or chill, etc. If we give an estimate of
an average of 40 units on the board at a time, each with 4
possible states, then we get 440 combinations of properties
of those units, or about 1024. Now factor in the fact that
Prismata has about 100 units (so far) of which 8 are selected
randomly for purchase at the start of the game, and we have
about 1010 possible starting states in Prismata. In total, this
gives a conservative lower bound of 1074 as the state space
for Prismata.
Action Space The action space of a game can be a mea-
sure of its decision complexity: how many moves are pos-
sible from a given state? A turn in Prismata consists of 4
main strategic decisions: defense, activating abilities, unit
purchasing, and breaching enemy units. Even if we consider
18
policy used in a playout is not optimal, if both players fol-
low this policy to the end of the game from a given state the
winner probably had an advantage in the original state. The
Game function is used to perform this playout for evaluation.
Finally, an example of HPS using NegaMax as the top-
level search algorithm and Game playouts as the heuristic
evaluation method can be seen in Algorithm 1.
Prismata
Prismata is a strategy game developed by Lunarch Studios
which combines “concepts from real-time strategy games,
collectible card games, and table-top strategy games” (Lu-
narchStudios 2015). Prismata has the following game prop-
erties:
1. Two player - While Prismata does have single player puz-
zle and campaign modes, this paper will focus on the more
popular and competitive 1 vs. 1 form of Prismata
2. Alternating Move - Players take turns performing moves
like in Chess. However, turns may consists of multiple
actions taken by the same player (such as buying units or
attacking). The turn is over when the active player declares
no additional actions and passes, or a time limit is reached
3. Zero Sum - The outcome of a game of Prismata is a win,
loss or a draw (stalemate), with a winner being declared if
they have destroyed all enemy units.
4. Perfect Information - All players in Prismata have ac-
cess to all of the game’s information. There are no decks,
hands, or fog of war to keep information secret from your
opponent like in some other strategy games.
5. Deterministic - At the beginning of a game, a random set
of 5 or 8 units (depending on the game type) is added to the
base pool of purchasable units. After this randomization
of the initial state, all game rules are deterministic.
Game Description
In Prismata, each player controls a number of units and has a
set of resources which are generated by the units they control.
These resources can then be consumed to purchase additional
units which can eventually create enough attack power to de-
stroy enemy units. The main elements and rules of the game
are as follows:
1. Units: Each player in Prismata controls a number of units,
similar to a real-time strategy game. Players build up an
army by purchasing additional units throughout the game
in order to attack the enemy player and defend from in-
coming attacks. There are dozens of unique unit types in
the game, with each player being able to purchase multi-
ple instances of each unit type, similar to how a player in
a real-time strategy game can have multiple instances of
unit such as a tank or a marine. Each unit type in Prismata
has a number of properties such as initial hit points, life
span, whether or not it can block, etc.
2. Abilities: Each unit type has a unique set of abilities which
allow it to perform specific actions such as: produce re-
sources, increase attack, defend, or kill / create other units.
The most basic and important unit of any Prismata game
is the Drone, whose ability can be used by the player to
produce one gold resource. Unit abilities can only be ac-
tivated once per turn during the action phase.
3. Resources: There are 6 resource types in Prismata: gold,
energy, red, blue, green, and attack. The gold and green
resource types accumulate from turn to turn, while energy,
red, and blue are depleted at the end of a turn. Attack is a
special resource and is explained in the next section. Play-
ers may choose to consume resources in order to purchase
additional units or activate unit abilities.
4. Combat: The goal of Prismata is to destroy all enemy
units. Combat in Prismata consists of two main steps: At-
tacking and Blocking. Unlike most strategy games, units
do not specifically attack other units, instead a unit gener-
ates an amount of attack which is summed with all other
attacking units into a single attack amount. Any amount of
Attack generated by units during a player’s turn must be
assigned by the enemy to their defensive units (blocked)
during the Defense phase of their next turn. When a de-
fensive player chooses a blocker with h health to defend
against a incoming attack: if a ≥ h the blocking unit is
destroyed and the process repeats witha−h remaining at-
tack. If a = 0or a < hthe blocking unit lives and the de-
fense phase is complete. If a player generates more attack
than their opponent can block, then all enemy blockers are
destroyed and the attacking player enters the Breach phase
where remaining damage is assigned to enemy units of the
attacker’s choosing.
AI Challenges
Prismata is a challenging game to write an AI for, mainly
due to its large state and action spaces which create unique
challenges for even state-of-the-art search algorithms.
State Space The state space of a game (how many board
positions are possible) is often used as an intuitive measure
of game complexity. In Prismata, we can calculate a rough
estimate of the state space as follows. In a typical Base +
8 game players have access to 11 base units and 8 random
units, for a total of 19 units per player, or 38 in total. If we
give a conservative average supply limit of 10 per unit per
player, then the number of possible combinations of units
on the board at one time in Prismata is approximately 1040.
We then have to consider that each unit can have different
properties: can be used or unused, have different amounts of
hit points, stamina, or chill, etc. If we give an estimate of
an average of 40 units on the board at a time, each with 4
possible states, then we get 440 combinations of properties
of those units, or about 1024. Now factor in the fact that
Prismata has about 100 units (so far) of which 8 are selected
randomly for purchase at the start of the game, and we have
about 1010 possible starting states in Prismata. In total, this
gives a conservative lower bound of 1074 as the state space
for Prismata.
Action Space The action space of a game can be a mea-
sure of its decision complexity: how many moves are pos-
sible from a given state? A turn in Prismata consists of 4
main strategic decisions: defense, activating abilities, unit
purchasing, and breaching enemy units. Even if we consider
18

these problems as independent, each of them has an exponen-
tial number of possible sequences of actions. Consider just
the buying of units: given just 8 gold and 2 energy there are
18 possible ways to buy units from the base set alone. With
a typical mid-game resource count of 20 gold, 2 energy, 2
green, 2 blue, and 4 red there are over 25,000 possible base-
set combinations of purchases within a turn. Combining all
game phases, it is possible to have millions of legal action
combinations for a given turn.
Sub-Game Complexity While state and action spaces are
typically used as intuitive indicators of a game’s complex-
ity, they do not prove that finding optimal moves in a game
is computationally difficult. In order to further demonstrate
the complexity of Prismata, we show that well known com-
putationally hard problems can be polynomial-time reduced
to several strategic sub-components of the game:
When deciding which strategic units to purchase, expert
players will also attempt to maximize the amount of re-
sources spent on a given turn in order to minimize waste.
Given a set of resources and a set of purchasable units with
unique costs, the optimization problem of deciding which
sequence of unit purchases sum to the most total spent re-
sources is equivalent to the well known Knapsack prob-
lem, which is NP-hard. Also, when deciding how to defend
against an incoming attack, expert players will often attempt
to let less expensive units die while saving more costly and
strategically valuable units. The process of blocking in Pris-
mata involves splitting a total incoming integer attack amount
among defenders each with an integer amount of hit points.
The optimization problem of determining which blocking as-
signment leads to the least expensive total unit deaths is a
bin-packing problem, which is also NP-hard.
Prismata AI System
This section describes the Prismata AI system architecture
as well as how HPS is applied to Prismata.
AI Environment and Implementation
Prismata is currently written in ActionScript and played in a
browser using Flash, which is a notoriously slow language
for CPU intensive algorithms. The heuristic search algo-
rithms proposed require the ability to do fast forward simu-
lation and back-tracking of game states. To accomplish this,
the Prismata AI system and the entire Prismata game engine
were re-written in C++ and optimized for speed. This C++
code was then compiled to a JavaScript library using em-
scripten (EmscriptenProject 2014), resulting in code which
runs approximately 5 times slower than native C++, or about
20 times faster than ActionScript. This AI system stays idle
in a JavaScript worker thread until it is called by the Prismata
ActionScript engine. At the beginning of each AI turn, the
ActionScript game engine sends the current game state and
AI parameters to the JavaScript AI system, which after the
allotted time limit returns the chosen move. This threaded
approach allows the AI to think over multiple game anima-
tion frames without interrupting the player’s interaction with
the user interface.
Hierarchical Porfolio Search in Prismata
We will now describe how Hierarchical Portfolio Search is
applied to Prismata, which fortunately has some properties
which make this method especially powerful. Prismata has
3 distinct game phases: Defense, Action, and Breach, each
with their own rules and set of goals. In the defense phase
you are trying to most efficiently keep your units alive from
enemy attack, in the action phase you are trying to perform
actions to generate attack and kill your opponent, and in the
breach phase you are trying to most effectively destroy your
opponent’s units. We can break these 3 phases down even
further by considering the action phase as two separate sub-
phases: using abilities, and buying units, leaving us with 4
phases. While these phases are technically all part of the
same turn, even the best human players often consider them
as independent problems that they try to solve separately, as
the entire turn would be too much to mentally process at the
same time. We then develop a number of algorithms (Partial
Players) for attempting to choose good actions for each in-
dividual phase. For example, in the defense phase we could
have one Partial Player that tries to minimize the amount of
resources you will lose if you block a certain way, while an-
other would try to maximize the amount of attack you have
remaining to punish your opponent with.
Portfolio P = hP P1, P P2, P P3, P P4i
A set of Partial Players P Pi corresponding to each of the
four phases described above
This portfolio of Partial Players for each phase will now
serve as a move iterator for our high-level search algorithm to
search over all combinations of each move for each phase in
order to determine the best move for the turn. Once the port-
folio move iterator has been constructed, we use a high-level
search algorithm to decide which move combination to per-
form. The search algorithms used for the Prismata AI system
are UCT (Kocsis and Szepesvari 2006) and Alpha-Beta with
iterative deepening.
AI Configuration and Difficulty Settings
All AI components in Prismata can be modularly described
at a very high level in a text configuration file. This enables
easy modification of all AI components quickly and intu-
itively without the need to modify code or even recompile the
system. All components of the system can be modified in the
configuration: Players, Partial Players, Portfolios, Search Al-
gorithms, States, and Tournaments. These components are
arranged in a dictionary with a description of the component
as the key and collection of parameters as its value. Partial
Players are arranged via tactical category and can be com-
bined in any order to form full Players or Portfolios. Search
algorithm parameters such as search depth, time limits, eval-
uation methods, and portfolio move iterators are also speci-
fied here. Player specifications can also quickly be arranged
to play automatic AI vs. AI tournaments for strategic evalu-
ation, code benchmarking, or quality assurance testing.
Using the search configuration syntax, creating differ-
ent difficulty settings for the Prismata AI is trivial. After
the hardest difficulty had been created (Master Bot - us-
ing Monte-Carlo Tree Search), five other difficulty settings
were then created: Docile Bot (never attacks), Random Bot
19
tial number of possible sequences of actions. Consider just
the buying of units: given just 8 gold and 2 energy there are
18 possible ways to buy units from the base set alone. With
a typical mid-game resource count of 20 gold, 2 energy, 2
green, 2 blue, and 4 red there are over 25,000 possible base-
set combinations of purchases within a turn. Combining all
game phases, it is possible to have millions of legal action
combinations for a given turn.
Sub-Game Complexity While state and action spaces are
typically used as intuitive indicators of a game’s complex-
ity, they do not prove that finding optimal moves in a game
is computationally difficult. In order to further demonstrate
the complexity of Prismata, we show that well known com-
putationally hard problems can be polynomial-time reduced
to several strategic sub-components of the game:
When deciding which strategic units to purchase, expert
players will also attempt to maximize the amount of re-
sources spent on a given turn in order to minimize waste.
Given a set of resources and a set of purchasable units with
unique costs, the optimization problem of deciding which
sequence of unit purchases sum to the most total spent re-
sources is equivalent to the well known Knapsack prob-
lem, which is NP-hard. Also, when deciding how to defend
against an incoming attack, expert players will often attempt
to let less expensive units die while saving more costly and
strategically valuable units. The process of blocking in Pris-
mata involves splitting a total incoming integer attack amount
among defenders each with an integer amount of hit points.
The optimization problem of determining which blocking as-
signment leads to the least expensive total unit deaths is a
bin-packing problem, which is also NP-hard.
Prismata AI System
This section describes the Prismata AI system architecture
as well as how HPS is applied to Prismata.
AI Environment and Implementation
Prismata is currently written in ActionScript and played in a
browser using Flash, which is a notoriously slow language
for CPU intensive algorithms. The heuristic search algo-
rithms proposed require the ability to do fast forward simu-
lation and back-tracking of game states. To accomplish this,
the Prismata AI system and the entire Prismata game engine
were re-written in C++ and optimized for speed. This C++
code was then compiled to a JavaScript library using em-
scripten (EmscriptenProject 2014), resulting in code which
runs approximately 5 times slower than native C++, or about
20 times faster than ActionScript. This AI system stays idle
in a JavaScript worker thread until it is called by the Prismata
ActionScript engine. At the beginning of each AI turn, the
ActionScript game engine sends the current game state and
AI parameters to the JavaScript AI system, which after the
allotted time limit returns the chosen move. This threaded
approach allows the AI to think over multiple game anima-
tion frames without interrupting the player’s interaction with
the user interface.
Hierarchical Porfolio Search in Prismata
We will now describe how Hierarchical Portfolio Search is
applied to Prismata, which fortunately has some properties
which make this method especially powerful. Prismata has
3 distinct game phases: Defense, Action, and Breach, each
with their own rules and set of goals. In the defense phase
you are trying to most efficiently keep your units alive from
enemy attack, in the action phase you are trying to perform
actions to generate attack and kill your opponent, and in the
breach phase you are trying to most effectively destroy your
opponent’s units. We can break these 3 phases down even
further by considering the action phase as two separate sub-
phases: using abilities, and buying units, leaving us with 4
phases. While these phases are technically all part of the
same turn, even the best human players often consider them
as independent problems that they try to solve separately, as
the entire turn would be too much to mentally process at the
same time. We then develop a number of algorithms (Partial
Players) for attempting to choose good actions for each in-
dividual phase. For example, in the defense phase we could
have one Partial Player that tries to minimize the amount of
resources you will lose if you block a certain way, while an-
other would try to maximize the amount of attack you have
remaining to punish your opponent with.
Portfolio P = hP P1, P P2, P P3, P P4i
A set of Partial Players P Pi corresponding to each of the
four phases described above
This portfolio of Partial Players for each phase will now
serve as a move iterator for our high-level search algorithm to
search over all combinations of each move for each phase in
order to determine the best move for the turn. Once the port-
folio move iterator has been constructed, we use a high-level
search algorithm to decide which move combination to per-
form. The search algorithms used for the Prismata AI system
are UCT (Kocsis and Szepesvari 2006) and Alpha-Beta with
iterative deepening.
AI Configuration and Difficulty Settings
All AI components in Prismata can be modularly described
at a very high level in a text configuration file. This enables
easy modification of all AI components quickly and intu-
itively without the need to modify code or even recompile the
system. All components of the system can be modified in the
configuration: Players, Partial Players, Portfolios, Search Al-
gorithms, States, and Tournaments. These components are
arranged in a dictionary with a description of the component
as the key and collection of parameters as its value. Partial
Players are arranged via tactical category and can be com-
bined in any order to form full Players or Portfolios. Search
algorithm parameters such as search depth, time limits, eval-
uation methods, and portfolio move iterators are also speci-
fied here. Player specifications can also quickly be arranged
to play automatic AI vs. AI tournaments for strategic evalu-
ation, code benchmarking, or quality assurance testing.
Using the search configuration syntax, creating differ-
ent difficulty settings for the Prismata AI is trivial. After
the hardest difficulty had been created (Master Bot - us-
ing Monte-Carlo Tree Search), five other difficulty settings
were then created: Docile Bot (never attacks), Random Bot
19
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

(random moves), Easy Bot (makes moor defensive choices),
Medium Bot (makes poor unit purchase choices), and Ex-
pert Bot (performs a 2-ply alpha-beta search). All of these
difficulties were created in less than 15 minutes simply by
creating new combinations of Partial Players within the AI
settings file. Only the Expert and Master difficulty settings
use Hierarchical Portfolio Search.
Experiments
Several experiments were performed to evaluate the pro-
posed AI architecture and algorithms. All computational
experiments were performed on an Intel i7-3770k CPU @
3.50GHz running Windows 7.
AI vs. Human Players
Prismata’s most competitive format is its ranked ladder
system in which human players get paired against similar
skilled opponents through a automated match-making sys-
tem. Player skill is determined via a ranking system in which
players start at Tier 1 and progress by winning to Tier 10, at
which point players are ranked within tier 10 with an ELO-
like numerical rating. To test the strength of the AI vs. hu-
man opponents in an unbiased fashion, an experiment was
conducted in which the AI was configured to secretly play
games in the human ranked matchmaking system over the
course of a 48 hour period. Going by the name “MyNameIs-
Jeff”, the AI system was given randomized clicking timers
in order to more closely resemble the clicking patterns of a
human player. The AI player used was the in-game Master
Bot, which used UCT as its high-level search with a 3 second
time limit. During the period the AI played approximate 200
games against human opponents with no player realizing (or
at least verbalizing) that they were playing against a com-
puter controlled opponent. After the games were finished,
the bot achieved a ranking of Tier 6 with 48% progression
toward Tier 7. The distribution of player tier rankings at that
time is shown in Table 1, placing the bot’s skill within the
top 25% of human players on the Prismata ranked ladder.
Difficulty Settings
Two experiments were performed to test the playing strength
of various difficulty settings of the Prismata AI bots. The
first experiment was conducted to test if the playing strength
rank of the various difficulty settings matched their descrip-
tive rank. Descriptions of each bot difficulty are as follows:
Master - Uses a Portfolio of 12 Partial Players and does a
3000ms UCT search within HPS, chosen as a balance be-
tween search strength and player wait time
UCT X - Uses the same Portfolio as Master bot, does an X
millisecond UCT search within HPS
AB X - Uses the same Portfolio as Master bot, does an X
millisecond AlphaBeta search within HPS
Expert - Uses the same Portfolio as Master Bot, does a 2-ply
fixed depth alpha beta search within HPS
Medium - Picks a random move from Master Bot’s Portfolio
Easy - Medium, but with weaker defensive purchasing
Table 1: Prismata Player Ranking Distribution
Tier 1 2 3 4 5 6 7 8 9 10
Player Perc. 33.9 17.3 7.1 7.5 6.7 7.5 6.5 5.9 3.7 4.0
Table 2: Search vs. Difficulties Results (Row Win %)
UCT100 AB100 Expert Medium Easy Rnd. Avg.
UCT100 - 52.1 67.3 96.4 99.7 99.9 83.1
AB100 47.9 - 68.0 94.7 99.5 99.9 82.0
Expert 32.7 32.0 - 90.7 98.9 99.8 70.8
Medium 3.6 5.3 9.3 - 85.9 97.4 40.3
Easy 0.3 0.5 1.1 14.1 - 86.3 20.5
Random 0.1 0.1 0.2 2.6 13.7 - 3.3
Table 3: Search Algorithm Timing Results (Row Win %)
AB3k UCT3k AB1k UCT1k UCT100 AB100 Avg.
AB3k - 58.9 64.5 66.8 83.8 85.2 71.8
UCT3k 41.6 - 53.9 65.3 81.1 81.5 64.7
AB1k 35.5 46.3 - 58.1 76.3 80.2 59.3
UCT1k 33.4 34.8 41.9 - 70.1 74.1 50.9
UCT100 16.0 18.7 23.6 29.7 - 53.4 28.3
AB100 14.5 18.3 19.5 25.6 46.3 - 24.8
Random - All actions taken are randomly chosen until no
more legal actions remain and the turn is passed
Both UCT and AlphaBeta were chosen as the high-level
search algorithms for HPS, and in order to demonstrate the
performance of HPS under short time constraints their time
limits were set to 100ms per decision episode. 10,000 games
of base set + 8 random units were played between each pair-
ing, with a resulting score given for each pairing equal to
win% + (draw%/2). The results for this experiment are
shown in Table 2 and show that the difficulties do indeed
rank in the order that they were intended. It also shows
that at short time controls both UCT and AlphaBeta perform
equally well.
The second experiment tested the relative performance of
UCT and Alpha-Beta at different time settings in order to
determine how an increase in thinking time affects playing
strength. 1,000 games of base set + 8 random units were
played between all pairings of AlphaBeta and UCT, each
with time limits of 3000ms, 1000ms and 100ms. Results are
shown in Table 3 and indicate that playing strength increases
dramatically as more time is given to each search method.
An interesting note is that AlphaBeta outperforms UCT at
longer time limits. We believe that this is in part caused by
the fact that all players use the same portfolio as the basis
for their move iteration, therefore AlphaBeta may have an
advantage over our UCT implementation which does not yet
perform sub-tree solving.
User Survey
A user survey was conducted to evaluate whether or not the
design goals of the Prismata AI system had been met from a
user perspective. The following questions were asked about
20
Medium Bot (makes poor unit purchase choices), and Ex-
pert Bot (performs a 2-ply alpha-beta search). All of these
difficulties were created in less than 15 minutes simply by
creating new combinations of Partial Players within the AI
settings file. Only the Expert and Master difficulty settings
use Hierarchical Portfolio Search.
Experiments
Several experiments were performed to evaluate the pro-
posed AI architecture and algorithms. All computational
experiments were performed on an Intel i7-3770k CPU @
3.50GHz running Windows 7.
AI vs. Human Players
Prismata’s most competitive format is its ranked ladder
system in which human players get paired against similar
skilled opponents through a automated match-making sys-
tem. Player skill is determined via a ranking system in which
players start at Tier 1 and progress by winning to Tier 10, at
which point players are ranked within tier 10 with an ELO-
like numerical rating. To test the strength of the AI vs. hu-
man opponents in an unbiased fashion, an experiment was
conducted in which the AI was configured to secretly play
games in the human ranked matchmaking system over the
course of a 48 hour period. Going by the name “MyNameIs-
Jeff”, the AI system was given randomized clicking timers
in order to more closely resemble the clicking patterns of a
human player. The AI player used was the in-game Master
Bot, which used UCT as its high-level search with a 3 second
time limit. During the period the AI played approximate 200
games against human opponents with no player realizing (or
at least verbalizing) that they were playing against a com-
puter controlled opponent. After the games were finished,
the bot achieved a ranking of Tier 6 with 48% progression
toward Tier 7. The distribution of player tier rankings at that
time is shown in Table 1, placing the bot’s skill within the
top 25% of human players on the Prismata ranked ladder.
Difficulty Settings
Two experiments were performed to test the playing strength
of various difficulty settings of the Prismata AI bots. The
first experiment was conducted to test if the playing strength
rank of the various difficulty settings matched their descrip-
tive rank. Descriptions of each bot difficulty are as follows:
Master - Uses a Portfolio of 12 Partial Players and does a
3000ms UCT search within HPS, chosen as a balance be-
tween search strength and player wait time
UCT X - Uses the same Portfolio as Master bot, does an X
millisecond UCT search within HPS
AB X - Uses the same Portfolio as Master bot, does an X
millisecond AlphaBeta search within HPS
Expert - Uses the same Portfolio as Master Bot, does a 2-ply
fixed depth alpha beta search within HPS
Medium - Picks a random move from Master Bot’s Portfolio
Easy - Medium, but with weaker defensive purchasing
Table 1: Prismata Player Ranking Distribution
Tier 1 2 3 4 5 6 7 8 9 10
Player Perc. 33.9 17.3 7.1 7.5 6.7 7.5 6.5 5.9 3.7 4.0
Table 2: Search vs. Difficulties Results (Row Win %)
UCT100 AB100 Expert Medium Easy Rnd. Avg.
UCT100 - 52.1 67.3 96.4 99.7 99.9 83.1
AB100 47.9 - 68.0 94.7 99.5 99.9 82.0
Expert 32.7 32.0 - 90.7 98.9 99.8 70.8
Medium 3.6 5.3 9.3 - 85.9 97.4 40.3
Easy 0.3 0.5 1.1 14.1 - 86.3 20.5
Random 0.1 0.1 0.2 2.6 13.7 - 3.3
Table 3: Search Algorithm Timing Results (Row Win %)
AB3k UCT3k AB1k UCT1k UCT100 AB100 Avg.
AB3k - 58.9 64.5 66.8 83.8 85.2 71.8
UCT3k 41.6 - 53.9 65.3 81.1 81.5 64.7
AB1k 35.5 46.3 - 58.1 76.3 80.2 59.3
UCT1k 33.4 34.8 41.9 - 70.1 74.1 50.9
UCT100 16.0 18.7 23.6 29.7 - 53.4 28.3
AB100 14.5 18.3 19.5 25.6 46.3 - 24.8
Random - All actions taken are randomly chosen until no
more legal actions remain and the turn is passed
Both UCT and AlphaBeta were chosen as the high-level
search algorithms for HPS, and in order to demonstrate the
performance of HPS under short time constraints their time
limits were set to 100ms per decision episode. 10,000 games
of base set + 8 random units were played between each pair-
ing, with a resulting score given for each pairing equal to
win% + (draw%/2). The results for this experiment are
shown in Table 2 and show that the difficulties do indeed
rank in the order that they were intended. It also shows
that at short time controls both UCT and AlphaBeta perform
equally well.
The second experiment tested the relative performance of
UCT and Alpha-Beta at different time settings in order to
determine how an increase in thinking time affects playing
strength. 1,000 games of base set + 8 random units were
played between all pairings of AlphaBeta and UCT, each
with time limits of 3000ms, 1000ms and 100ms. Results are
shown in Table 3 and indicate that playing strength increases
dramatically as more time is given to each search method.
An interesting note is that AlphaBeta outperforms UCT at
longer time limits. We believe that this is in part caused by
the fact that all players use the same portfolio as the basis
for their move iteration, therefore AlphaBeta may have an
advantage over our UCT implementation which does not yet
perform sub-tree solving.
User Survey
A user survey was conducted to evaluate whether or not the
design goals of the Prismata AI system had been met from a
user perspective. The following questions were asked about
20
1 1 1 1 1 12 2 2 2 2 23 3 3 3 3 34 4 4 4 4 45 5 5 5 5 56 6 6 6 6 67 7 7 7 7 7
0
10
20
30
40
50
Question 1 Question 2 Question 3 Question 4 Question 5 Question 6
Number of Responses
Prismata AI Survey Response Histograms
mean = 6.13
median = 6
mean = 3.78
median = 4
mean = 5.34
median = 6
mean = 4.86
median = 5
mean = 5.47
median = 6
mean = 5.55
median = 6
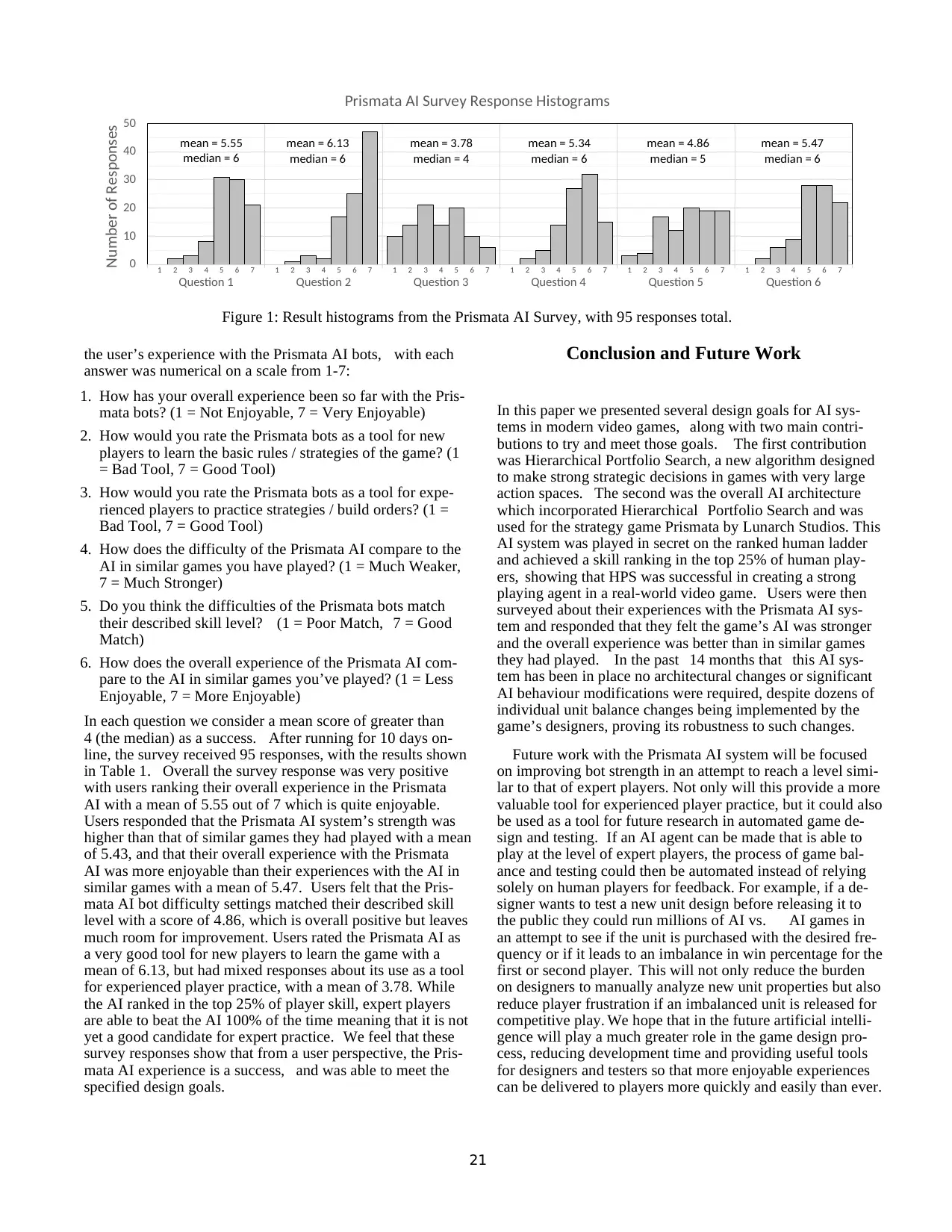
Figure 1: Result histograms from the Prismata AI Survey, with 95 responses total.
the user’s experience with the Prismata AI bots, with each
answer was numerical on a scale from 1-7:
1. How has your overall experience been so far with the Pris-
mata bots? (1 = Not Enjoyable, 7 = Very Enjoyable)
2. How would you rate the Prismata bots as a tool for new
players to learn the basic rules / strategies of the game? (1
= Bad Tool, 7 = Good Tool)
3. How would you rate the Prismata bots as a tool for expe-
rienced players to practice strategies / build orders? (1 =
Bad Tool, 7 = Good Tool)
4. How does the difficulty of the Prismata AI compare to the
AI in similar games you have played? (1 = Much Weaker,
7 = Much Stronger)
5. Do you think the difficulties of the Prismata bots match
their described skill level? (1 = Poor Match, 7 = Good
Match)
6. How does the overall experience of the Prismata AI com-
pare to the AI in similar games you’ve played? (1 = Less
Enjoyable, 7 = More Enjoyable)
In each question we consider a mean score of greater than
4 (the median) as a success. After running for 10 days on-
line, the survey received 95 responses, with the results shown
in Table 1. Overall the survey response was very positive
with users ranking their overall experience in the Prismata
AI with a mean of 5.55 out of 7 which is quite enjoyable.
Users responded that the Prismata AI system’s strength was
higher than that of similar games they had played with a mean
of 5.43, and that their overall experience with the Prismata
AI was more enjoyable than their experiences with the AI in
similar games with a mean of 5.47. Users felt that the Pris-
mata AI bot difficulty settings matched their described skill
level with a score of 4.86, which is overall positive but leaves
much room for improvement. Users rated the Prismata AI as
a very good tool for new players to learn the game with a
mean of 6.13, but had mixed responses about its use as a tool
for experienced player practice, with a mean of 3.78. While
the AI ranked in the top 25% of player skill, expert players
are able to beat the AI 100% of the time meaning that it is not
yet a good candidate for expert practice. We feel that these
survey responses show that from a user perspective, the Pris-
mata AI experience is a success, and was able to meet the
specified design goals.
Conclusion and Future Work
In this paper we presented several design goals for AI sys-
tems in modern video games, along with two main contri-
butions to try and meet those goals. The first contribution
was Hierarchical Portfolio Search, a new algorithm designed
to make strong strategic decisions in games with very large
action spaces. The second was the overall AI architecture
which incorporated Hierarchical Portfolio Search and was
used for the strategy game Prismata by Lunarch Studios. This
AI system was played in secret on the ranked human ladder
and achieved a skill ranking in the top 25% of human play-
ers, showing that HPS was successful in creating a strong
playing agent in a real-world video game. Users were then
surveyed about their experiences with the Prismata AI sys-
tem and responded that they felt the game’s AI was stronger
and the overall experience was better than in similar games
they had played. In the past 14 months that this AI sys-
tem has been in place no architectural changes or significant
AI behaviour modifications were required, despite dozens of
individual unit balance changes being implemented by the
game’s designers, proving its robustness to such changes.
Future work with the Prismata AI system will be focused
on improving bot strength in an attempt to reach a level simi-
lar to that of expert players. Not only will this provide a more
valuable tool for experienced player practice, but it could also
be used as a tool for future research in automated game de-
sign and testing. If an AI agent can be made that is able to
play at the level of expert players, the process of game bal-
ance and testing could then be automated instead of relying
solely on human players for feedback. For example, if a de-
signer wants to test a new unit design before releasing it to
the public they could run millions of AI vs. AI games in
an attempt to see if the unit is purchased with the desired fre-
quency or if it leads to an imbalance in win percentage for the
first or second player. This will not only reduce the burden
on designers to manually analyze new unit properties but also
reduce player frustration if an imbalanced unit is released for
competitive play. We hope that in the future artificial intelli-
gence will play a much greater role in the game design pro-
cess, reducing development time and providing useful tools
for designers and testers so that more enjoyable experiences
can be delivered to players more quickly and easily than ever.
21
0
10
20
30
40
50
Question 1 Question 2 Question 3 Question 4 Question 5 Question 6
Number of Responses
Prismata AI Survey Response Histograms
mean = 6.13
median = 6
mean = 3.78
median = 4
mean = 5.34
median = 6
mean = 4.86
median = 5
mean = 5.47
median = 6
mean = 5.55
median = 6
Figure 1: Result histograms from the Prismata AI Survey, with 95 responses total.
the user’s experience with the Prismata AI bots, with each
answer was numerical on a scale from 1-7:
1. How has your overall experience been so far with the Pris-
mata bots? (1 = Not Enjoyable, 7 = Very Enjoyable)
2. How would you rate the Prismata bots as a tool for new
players to learn the basic rules / strategies of the game? (1
= Bad Tool, 7 = Good Tool)
3. How would you rate the Prismata bots as a tool for expe-
rienced players to practice strategies / build orders? (1 =
Bad Tool, 7 = Good Tool)
4. How does the difficulty of the Prismata AI compare to the
AI in similar games you have played? (1 = Much Weaker,
7 = Much Stronger)
5. Do you think the difficulties of the Prismata bots match
their described skill level? (1 = Poor Match, 7 = Good
Match)
6. How does the overall experience of the Prismata AI com-
pare to the AI in similar games you’ve played? (1 = Less
Enjoyable, 7 = More Enjoyable)
In each question we consider a mean score of greater than
4 (the median) as a success. After running for 10 days on-
line, the survey received 95 responses, with the results shown
in Table 1. Overall the survey response was very positive
with users ranking their overall experience in the Prismata
AI with a mean of 5.55 out of 7 which is quite enjoyable.
Users responded that the Prismata AI system’s strength was
higher than that of similar games they had played with a mean
of 5.43, and that their overall experience with the Prismata
AI was more enjoyable than their experiences with the AI in
similar games with a mean of 5.47. Users felt that the Pris-
mata AI bot difficulty settings matched their described skill
level with a score of 4.86, which is overall positive but leaves
much room for improvement. Users rated the Prismata AI as
a very good tool for new players to learn the game with a
mean of 6.13, but had mixed responses about its use as a tool
for experienced player practice, with a mean of 3.78. While
the AI ranked in the top 25% of player skill, expert players
are able to beat the AI 100% of the time meaning that it is not
yet a good candidate for expert practice. We feel that these
survey responses show that from a user perspective, the Pris-
mata AI experience is a success, and was able to meet the
specified design goals.
Conclusion and Future Work
In this paper we presented several design goals for AI sys-
tems in modern video games, along with two main contri-
butions to try and meet those goals. The first contribution
was Hierarchical Portfolio Search, a new algorithm designed
to make strong strategic decisions in games with very large
action spaces. The second was the overall AI architecture
which incorporated Hierarchical Portfolio Search and was
used for the strategy game Prismata by Lunarch Studios. This
AI system was played in secret on the ranked human ladder
and achieved a skill ranking in the top 25% of human play-
ers, showing that HPS was successful in creating a strong
playing agent in a real-world video game. Users were then
surveyed about their experiences with the Prismata AI sys-
tem and responded that they felt the game’s AI was stronger
and the overall experience was better than in similar games
they had played. In the past 14 months that this AI sys-
tem has been in place no architectural changes or significant
AI behaviour modifications were required, despite dozens of
individual unit balance changes being implemented by the
game’s designers, proving its robustness to such changes.
Future work with the Prismata AI system will be focused
on improving bot strength in an attempt to reach a level simi-
lar to that of expert players. Not only will this provide a more
valuable tool for experienced player practice, but it could also
be used as a tool for future research in automated game de-
sign and testing. If an AI agent can be made that is able to
play at the level of expert players, the process of game bal-
ance and testing could then be automated instead of relying
solely on human players for feedback. For example, if a de-
signer wants to test a new unit design before releasing it to
the public they could run millions of AI vs. AI games in
an attempt to see if the unit is purchased with the desired fre-
quency or if it leads to an imbalance in win percentage for the
first or second player. This will not only reduce the burden
on designers to manually analyze new unit properties but also
reduce player frustration if an imbalanced unit is released for
competitive play. We hope that in the future artificial intelli-
gence will play a much greater role in the game design pro-
cess, reducing development time and providing useful tools
for designers and testers so that more enjoyable experiences
can be delivered to players more quickly and easily than ever.
21

References
Bowling, M.; Burch, N.; Johanson, M.; and Tammelin, O.
2015. Heads-up limit hold’em poker is solved. Science
347(6218):145–149.
Churchill, D., and Buro, M. 2013. Portfolio greedy search
and simulation for large-scale combat in StarCraft. In IEEE
Conference on Computational Intelligence in Games (CIG),
1–8. IEEE.
Churchill, D.; Saffidine, A.; and Buro, M. 2012. Fast heuris-
tic search for RTS game combat scenarios. In AI and Inter-
active Digital Entertainment Conference, AIIDE (AAAI).
EmscriptenProject. 2014. emscripten.
http://emscripten.org/.
Kocsis, L., and Szepesvari, C. 2006. Bandit based Monte-
Carlo planning. In Proceedings of the European Conference
on Machine Learning, 282–293.
LunarchStudios. 2015. Prismata. http://www.prismata.net/.
Schaeffer, J.; Lake, R.; Lu, P.; and Bryant, M. 1996. CHI-
NOOK: The world man-machine Checkers champion. AI
Magazine 17(1):21–29.
Wilson, A. R. 2012. Masters of
war: History’s greatest strategic thinkers.
http://www.thegreatcourses.com/tgc/courses/
course_detail.aspx?cid=9422.
22
Bowling, M.; Burch, N.; Johanson, M.; and Tammelin, O.
2015. Heads-up limit hold’em poker is solved. Science
347(6218):145–149.
Churchill, D., and Buro, M. 2013. Portfolio greedy search
and simulation for large-scale combat in StarCraft. In IEEE
Conference on Computational Intelligence in Games (CIG),
1–8. IEEE.
Churchill, D.; Saffidine, A.; and Buro, M. 2012. Fast heuris-
tic search for RTS game combat scenarios. In AI and Inter-
active Digital Entertainment Conference, AIIDE (AAAI).
EmscriptenProject. 2014. emscripten.
http://emscripten.org/.
Kocsis, L., and Szepesvari, C. 2006. Bandit based Monte-
Carlo planning. In Proceedings of the European Conference
on Machine Learning, 282–293.
LunarchStudios. 2015. Prismata. http://www.prismata.net/.
Schaeffer, J.; Lake, R.; Lu, P.; and Bryant, M. 1996. CHI-
NOOK: The world man-machine Checkers champion. AI
Magazine 17(1):21–29.
Wilson, A. R. 2012. Masters of
war: History’s greatest strategic thinkers.
http://www.thegreatcourses.com/tgc/courses/
course_detail.aspx?cid=9422.
22
1 out of 7
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
