Comprehensive Analysis of Hire Purchase and Compound Interest Problems
VerifiedAdded on 2023/06/06
|15
|2137
|254
Homework Assignment
AI Summary
This assignment provides detailed solutions to various financial mathematics problems, covering hire purchase agreements, compound interest calculations, and effective interest rates. The solutions include step-by-step calculations for determining total interest paid, monthly repayments, and total costs associated with hire purchase contracts. The assignment also explores compound interest scenarios, including annual, daily, and monthly compounding, and utilizes financial tables to calculate loan installments and analyze different loan terms. Furthermore, the document examines effective interest rates and compares offers from different lending institutions. The content includes worked examples and calculations to help students understand the concepts of financial mathematics and apply them to practical situations, such as calculating loan repayments and comparing different loan options. The assignment concludes with a section on using tables for interest repayments and applying the concepts to real-world scenarios.

MATHEMATICAL SOLUTION
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

PART A:
EXAMPLE: A sapphire earing with marked price of $1800 is offered to the purchaser on the
following terms: $200 deposit and balance to be paid over 24equal monthly instalments with
interest charged at 11.5% flat rate. Find:
a) Total interest paid
b) The monthly repayments
c) The total cost of car
Solution:
a) Cash price = $1,800
Deposit = $200
Balance to pay = $1,600
Interest (I )= ( 1600 × 11.5× 2 )
100
Interest paid ( I)=$ 368
b) The monthly repayments = Balance +interest
no . of periods
= $ 1968
24 = $ 82
c) The total cost of car = Deposit + Loanbalance+Interest
= 200+1600+368 = $ 21,368
EXAMPLE: A sapphire earing with marked price of $1800 is offered to the purchaser on the
following terms: $200 deposit and balance to be paid over 24equal monthly instalments with
interest charged at 11.5% flat rate. Find:
a) Total interest paid
b) The monthly repayments
c) The total cost of car
Solution:
a) Cash price = $1,800
Deposit = $200
Balance to pay = $1,600
Interest (I )= ( 1600 × 11.5× 2 )
100
Interest paid ( I)=$ 368
b) The monthly repayments = Balance +interest
no . of periods
= $ 1968
24 = $ 82
c) The total cost of car = Deposit + Loanbalance+Interest
= 200+1600+368 = $ 21,368

Question 1
A car is purchased on hire purchase. The cash price is $21,000 and the terms are, a deposit of
10% of the cash price, then the balance to be paid off over 60 equal monthly instalments. Interest
is charged at 12% p.a
a) Calculate the deposit and the balance
Deposit=10 % of $ 21,00
= 0.1 ×21,000= $2,100
Loan balance=$ ¿) = $18,900
b) Calculate the interest paid on the balance
Interest charged= 18,900× 12×5
100
Interest ctharged=$ 11,340
c) Calculate the monthly instalments
Total instalments=Loanbalance+interest paid
= 18,900 + 11,340= $30,240
Monthly instalments= 30,240
60 = $504
d) Calculate the total cost of the car.
Total Cost =¿
= $(2,100 +18,900 + 11,340) =$32,340
Question 2
The cash price of a suit is $2,000. If a customer pays a deposit of $300 and pays equal monthly
instalments of $60 over 2.5 years, calculate:
a) The amount of interest charged
Solution
A car is purchased on hire purchase. The cash price is $21,000 and the terms are, a deposit of
10% of the cash price, then the balance to be paid off over 60 equal monthly instalments. Interest
is charged at 12% p.a
a) Calculate the deposit and the balance
Deposit=10 % of $ 21,00
= 0.1 ×21,000= $2,100
Loan balance=$ ¿) = $18,900
b) Calculate the interest paid on the balance
Interest charged= 18,900× 12×5
100
Interest ctharged=$ 11,340
c) Calculate the monthly instalments
Total instalments=Loanbalance+interest paid
= 18,900 + 11,340= $30,240
Monthly instalments= 30,240
60 = $504
d) Calculate the total cost of the car.
Total Cost =¿
= $(2,100 +18,900 + 11,340) =$32,340
Question 2
The cash price of a suit is $2,000. If a customer pays a deposit of $300 and pays equal monthly
instalments of $60 over 2.5 years, calculate:
a) The amount of interest charged
Solution
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Loan balance=(2,000−300) = $1,700
Monthly instalments = 1,700+ Interest
2.5 ×12
Since monthly instalments = $60,
Therefore, $ 60= 1,700+ Interest
30
$1,800 = $1,700 – Interest
Interest charged = $100
b) The total paid for the suit.
Total amount = Deposit + Loan balance (Principal) + Interest
= $(300 +1,700 +100) = $2,100
Question 3
An electric guitar is being bought on hire purchase for a $250 deposit and monthly instalments of
$78.50 for 3 years. The cash price for this guitar is $2,500. Find the interest rate charged by the
shop.
Solution
Deposit = $250
Monthly instalments = $78.50
Cash price = $2,500
Principal = Cash price – Deposit
= $(2,500 – 250)= $2,250
Monthly instalments = 1,700+ Interest
2.5 ×12
Since monthly instalments = $60,
Therefore, $ 60= 1,700+ Interest
30
$1,800 = $1,700 – Interest
Interest charged = $100
b) The total paid for the suit.
Total amount = Deposit + Loan balance (Principal) + Interest
= $(300 +1,700 +100) = $2,100
Question 3
An electric guitar is being bought on hire purchase for a $250 deposit and monthly instalments of
$78.50 for 3 years. The cash price for this guitar is $2,500. Find the interest rate charged by the
shop.
Solution
Deposit = $250
Monthly instalments = $78.50
Cash price = $2,500
Principal = Cash price – Deposit
= $(2,500 – 250)= $2,250
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
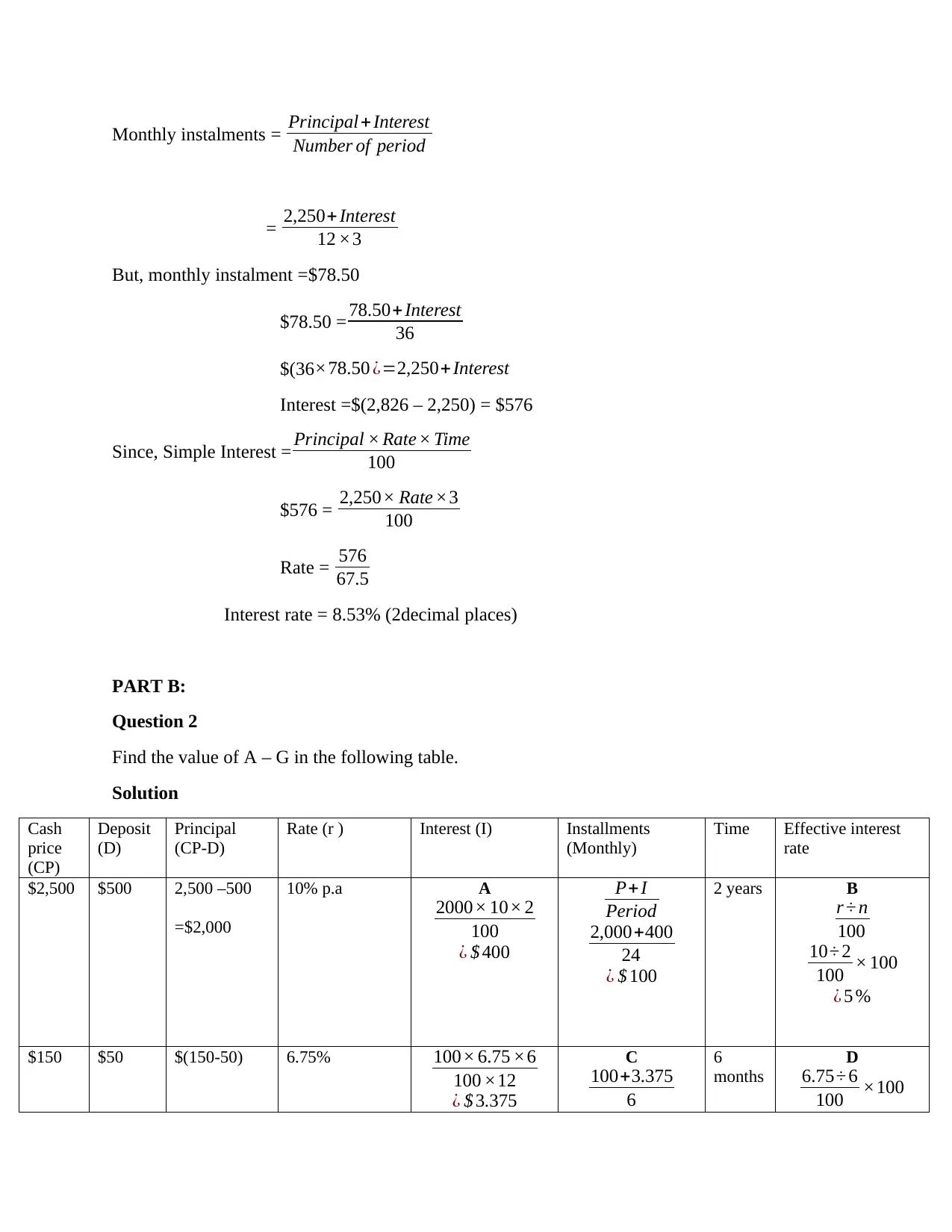
Monthly instalments = Principal + Interest
Number of period
= 2,250+ Interest
12 ×3
But, monthly instalment =$78.50
$78.50 = 78.50+Interest
36
$(36×78.50 ¿=2,250+ Interest
Interest =$(2,826 – 2,250) = $576
Since, Simple Interest = Principal × Rate × Time
100
$576 = 2,250× Rate ×3
100
Rate = 576
67.5
Interest rate = 8.53% (2decimal places)
PART B:
Question 2
Find the value of A – G in the following table.
Solution
Cash
price
(CP)
Deposit
(D)
Principal
(CP-D)
Rate (r ) Interest (I) Installments
(Monthly)
Time Effective interest
rate
$2,500 $500 2,500 –500
=$2,000
10% p.a A
2000× 10× 2
100
¿ $ 400
P+I
Period
2,000+400
24
¿ $ 100
2 years B
r ÷ n
100
10÷ 2
100 × 100
¿ 5 %
$150 $50 $(150-50) 6.75% 100× 6.75 ×6
100 ×12
¿ $ 3.375
C
100+3.375
6
6
months
D
6.75÷ 6
100 ×100
Number of period
= 2,250+ Interest
12 ×3
But, monthly instalment =$78.50
$78.50 = 78.50+Interest
36
$(36×78.50 ¿=2,250+ Interest
Interest =$(2,826 – 2,250) = $576
Since, Simple Interest = Principal × Rate × Time
100
$576 = 2,250× Rate ×3
100
Rate = 576
67.5
Interest rate = 8.53% (2decimal places)
PART B:
Question 2
Find the value of A – G in the following table.
Solution
Cash
price
(CP)
Deposit
(D)
Principal
(CP-D)
Rate (r ) Interest (I) Installments
(Monthly)
Time Effective interest
rate
$2,500 $500 2,500 –500
=$2,000
10% p.a A
2000× 10× 2
100
¿ $ 400
P+I
Period
2,000+400
24
¿ $ 100
2 years B
r ÷ n
100
10÷ 2
100 × 100
¿ 5 %
$150 $50 $(150-50) 6.75% 100× 6.75 ×6
100 ×12
¿ $ 3.375
C
100+3.375
6
6
months
D
6.75÷ 6
100 ×100

¿ $ 17.23 ¿ 1.125 %
$6,500 $1,500 6,500-1,500 F
500× r ×2
100 =1000
100 r=1000
r =10 %
5000× I
24 =250
¿ 6000−5000
E
$250
5000+ I
24 =250
2 years G
10÷ 2
100 × 100
¿ 5 %
Summarized solution
A B C D E F G
=$400 =5% =$17.23 =1.125% =$250(given) =10% =5%
PART C: Compound Interest
Compound interest is when you deposit money in an account and rather getting the same amount
of interest each year (simple interest), you receive interest on the new amount in your account at
the end of every period.
We use the formula:
A=P ( 1+ r
n )
nt
Where, r = annual rate, n = number of times of interest is added per year, t = number of years,
P=Principal, A=amount accrued in the bank
EXAMPLE
I borrow $1000 at 12% comp p.a I take the loan out for 3 years. Calculate the amount I will have
in the bank if interest is:
a) Compounded annually, n=1, interest is paid once a year, t=3years
A=1000 ( 1+ 0.12
3 )
3 × 1
= $1,404.93
$6,500 $1,500 6,500-1,500 F
500× r ×2
100 =1000
100 r=1000
r =10 %
5000× I
24 =250
¿ 6000−5000
E
$250
5000+ I
24 =250
2 years G
10÷ 2
100 × 100
¿ 5 %
Summarized solution
A B C D E F G
=$400 =5% =$17.23 =1.125% =$250(given) =10% =5%
PART C: Compound Interest
Compound interest is when you deposit money in an account and rather getting the same amount
of interest each year (simple interest), you receive interest on the new amount in your account at
the end of every period.
We use the formula:
A=P ( 1+ r
n )
nt
Where, r = annual rate, n = number of times of interest is added per year, t = number of years,
P=Principal, A=amount accrued in the bank
EXAMPLE
I borrow $1000 at 12% comp p.a I take the loan out for 3 years. Calculate the amount I will have
in the bank if interest is:
a) Compounded annually, n=1, interest is paid once a year, t=3years
A=1000 ( 1+ 0.12
3 )
3 × 1
= $1,404.93
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

b) Compounded daily, n=365, interest is paid 365days a year,t=3years
A=1000 ( 1+ 0.12
3 × 365 )
365× 3
= $ 1,433.24
c) Compounded monthly, n=12, interest is paid 12times a year
A=1000 ( 1+ 0.12
12 )
12 ×3
= $1,430.77
PART D: Compound interest from a table
Often a bank will provide a table rather than you having to use a formula in Part C above.
EXAMPLE
Using the financial table, calculate the monthly installments required to pay off a 25-year loan of
$110,000 at 4% p.a monthly reducible interest.
A = 5.28 ×110 × 12 months × 25 years = 174,240
Question 1
A=1000 ( 1+ 0.12
3 × 365 )
365× 3
= $ 1,433.24
c) Compounded monthly, n=12, interest is paid 12times a year
A=1000 ( 1+ 0.12
12 )
12 ×3
= $1,430.77
PART D: Compound interest from a table
Often a bank will provide a table rather than you having to use a formula in Part C above.
EXAMPLE
Using the financial table, calculate the monthly installments required to pay off a 25-year loan of
$110,000 at 4% p.a monthly reducible interest.
A = 5.28 ×110 × 12 months × 25 years = 174,240
Question 1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Calculate the annual instalments needed to pay off a $110,000 home loan at 7% p.a reducible
interest if the installments are to be paid in equal installments over 15 years. Give your answer to
nearest correct cents.
Solution
Number of lots = ( 110,000
1000 )=110
Installments = 110 ×109.79 ×1 ×15 = $181,153.50
Question 2
Mae received a 30-year $89,000 loan at 2% p.a monthly reducible interest if the term of the loan
was reduced to 25 years, calculate:
interest if the installments are to be paid in equal installments over 15 years. Give your answer to
nearest correct cents.
Solution
Number of lots = ( 110,000
1000 )=110
Installments = 110 ×109.79 ×1 ×15 = $181,153.50
Question 2
Mae received a 30-year $89,000 loan at 2% p.a monthly reducible interest if the term of the loan
was reduced to 25 years, calculate:

Solution
a) The amount of each monthly instalment over a 30-year loan term
Number of lots ¿ 89,000
1000 =89 lots
Monthly installment = 89 × 3.7 × 30 × 12 = $ 118,548
b) The monthly needed for a 25-year term
Monthly installment = 89 × 3.7 × 25 ×12 = $98,790
c) The amount saved, from this 5-year reduction in the term of the loan
Amount saved = $(118,548 – 98,790) = $19758.
Question 2
Using the financial table, calculate the monthly installments required to pay off a 25-year loan of
$1000 at 4% p.a monthly reducible interest.
a) The amount of each monthly instalment over a 30-year loan term
Number of lots ¿ 89,000
1000 =89 lots
Monthly installment = 89 × 3.7 × 30 × 12 = $ 118,548
b) The monthly needed for a 25-year term
Monthly installment = 89 × 3.7 × 25 ×12 = $98,790
c) The amount saved, from this 5-year reduction in the term of the loan
Amount saved = $(118,548 – 98,790) = $19758.
Question 2
Using the financial table, calculate the monthly installments required to pay off a 25-year loan of
$1000 at 4% p.a monthly reducible interest.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
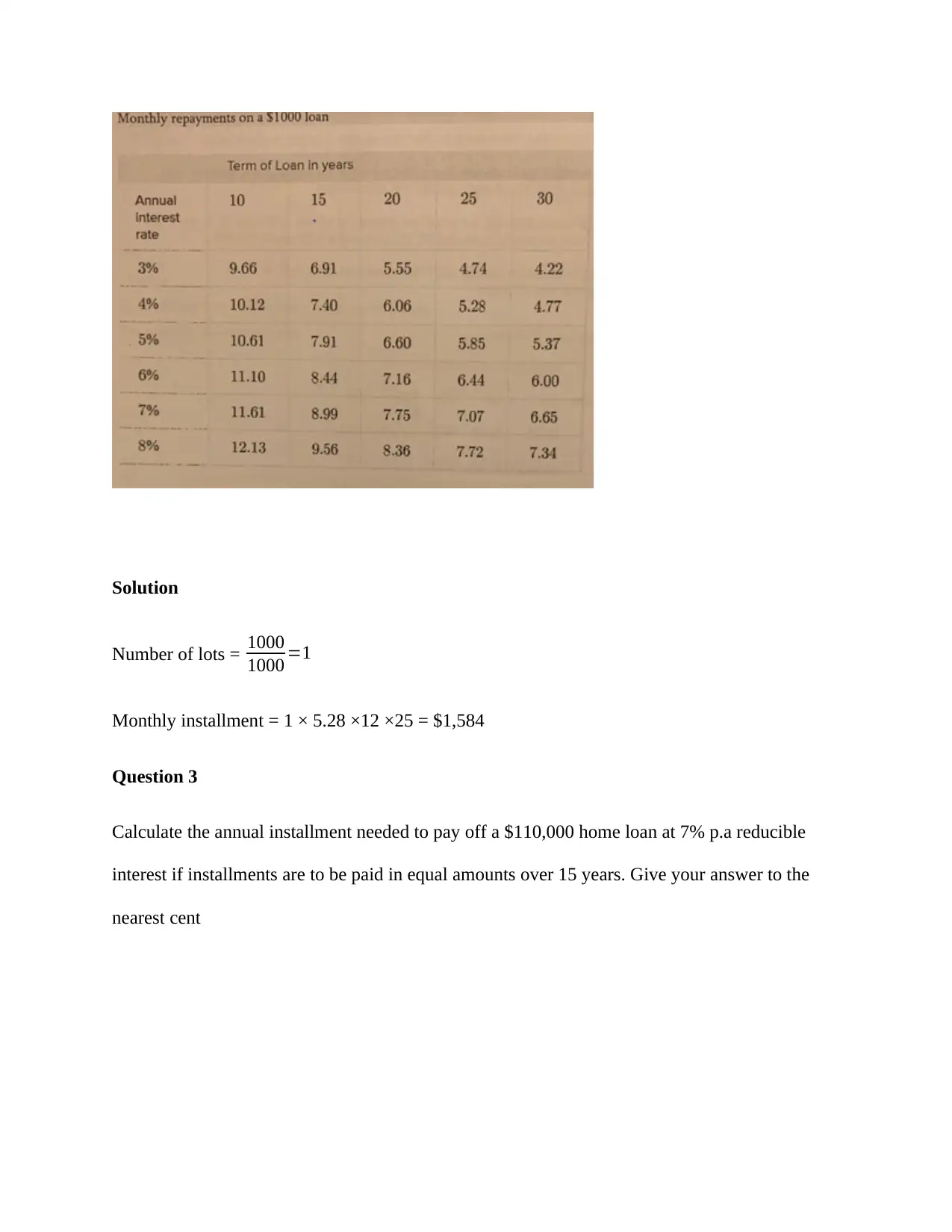
Solution
Number of lots = 1000
1000 =1
Monthly installment = 1 × 5.28 ×12 ×25 = $1,584
Question 3
Calculate the annual installment needed to pay off a $110,000 home loan at 7% p.a reducible
interest if installments are to be paid in equal amounts over 15 years. Give your answer to the
nearest cent
Number of lots = 1000
1000 =1
Monthly installment = 1 × 5.28 ×12 ×25 = $1,584
Question 3
Calculate the annual installment needed to pay off a $110,000 home loan at 7% p.a reducible
interest if installments are to be paid in equal amounts over 15 years. Give your answer to the
nearest cent
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Solution
Number of lots = 110,000
1000 = 110 lots
Annual installments = 110 × 109.79 ×1 ×15 = $181,153.50
PART E: Effective rate of interest ( Compound interest)
If I want to compare a bank account that compounds at different rates, then we can use the
following formula
E ffective interest rate= ( 1+ r /n
100 ) n
−1
EXAMPLE
Neil invested $3,500 at 4.3% p.a compounded daily. Find the effective interest rate
E ffective interest rate= ( 1+ 4.3/365
100 )
365
−1
Number of lots = 110,000
1000 = 110 lots
Annual installments = 110 × 109.79 ×1 ×15 = $181,153.50
PART E: Effective rate of interest ( Compound interest)
If I want to compare a bank account that compounds at different rates, then we can use the
following formula
E ffective interest rate= ( 1+ r /n
100 ) n
−1
EXAMPLE
Neil invested $3,500 at 4.3% p.a compounded daily. Find the effective interest rate
E ffective interest rate= ( 1+ 4.3/365
100 )
365
−1

= 0.0439 ×100% = 4.39%
Question 1
A loan attracts interest at a rate of 1.8% compounding annually. What is the effective rate correct
to one decimal place?
Solution
E ffective interest rate= ( 1+ 1.8 /1
100 )
1 ×1
−1
Effective interest rate = (1.018 – 1) ×100% = 1.8%
Question 2
Two different lending institutions are offering different rates on their loans. Betta Bank is
offering 4.4% compounding monthly. Lucky lending is offering 4.2% compounding quarterly.
a) What is the effective rate of Beta Bank correct to two decimal places?
Solution
E ffective interest rate= (1+ 4.4/12
100 )12
−1
E ffective interest rate= (1+ 0.3667
100 )12
−1
Effective interest rate = ( 1.003667 )12−1 ¿× 100 %
= (1.0449 – 1) ×100 % = 4.49% (2 decimal places)
b) What is effective rate of Lucky lending correct to two decimal places?
Question 1
A loan attracts interest at a rate of 1.8% compounding annually. What is the effective rate correct
to one decimal place?
Solution
E ffective interest rate= ( 1+ 1.8 /1
100 )
1 ×1
−1
Effective interest rate = (1.018 – 1) ×100% = 1.8%
Question 2
Two different lending institutions are offering different rates on their loans. Betta Bank is
offering 4.4% compounding monthly. Lucky lending is offering 4.2% compounding quarterly.
a) What is the effective rate of Beta Bank correct to two decimal places?
Solution
E ffective interest rate= (1+ 4.4/12
100 )12
−1
E ffective interest rate= (1+ 0.3667
100 )12
−1
Effective interest rate = ( 1.003667 )12−1 ¿× 100 %
= (1.0449 – 1) ×100 % = 4.49% (2 decimal places)
b) What is effective rate of Lucky lending correct to two decimal places?
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




