Hydrodynamic Solution: Comprehensive Analysis of Piping Systems Design

This assignment provides a detailed hydrodynamic solution for the analysis and design of piping systems. It includes calculations for the Reynolds number, friction factor, total head loss, and pump power requirements. The solution covers various aspects such as determining the total head loss in the system, calculating flow velocities in different pipes, and determining the power absorbed due to viscous friction. Furthermore, the assignment delves into the hydraulic radius calculation and the minimum angle of inclination for a channel. The solution uses the Darcy equation, continuity equation, and other relevant formulas to provide a comprehensive analysis of the fluid flow and pressure drop in the system. This assignment is designed to help students understand the principles of fluid dynamics and apply them to real-world engineering problems.

HYDRODYNAMIC SOLUTION
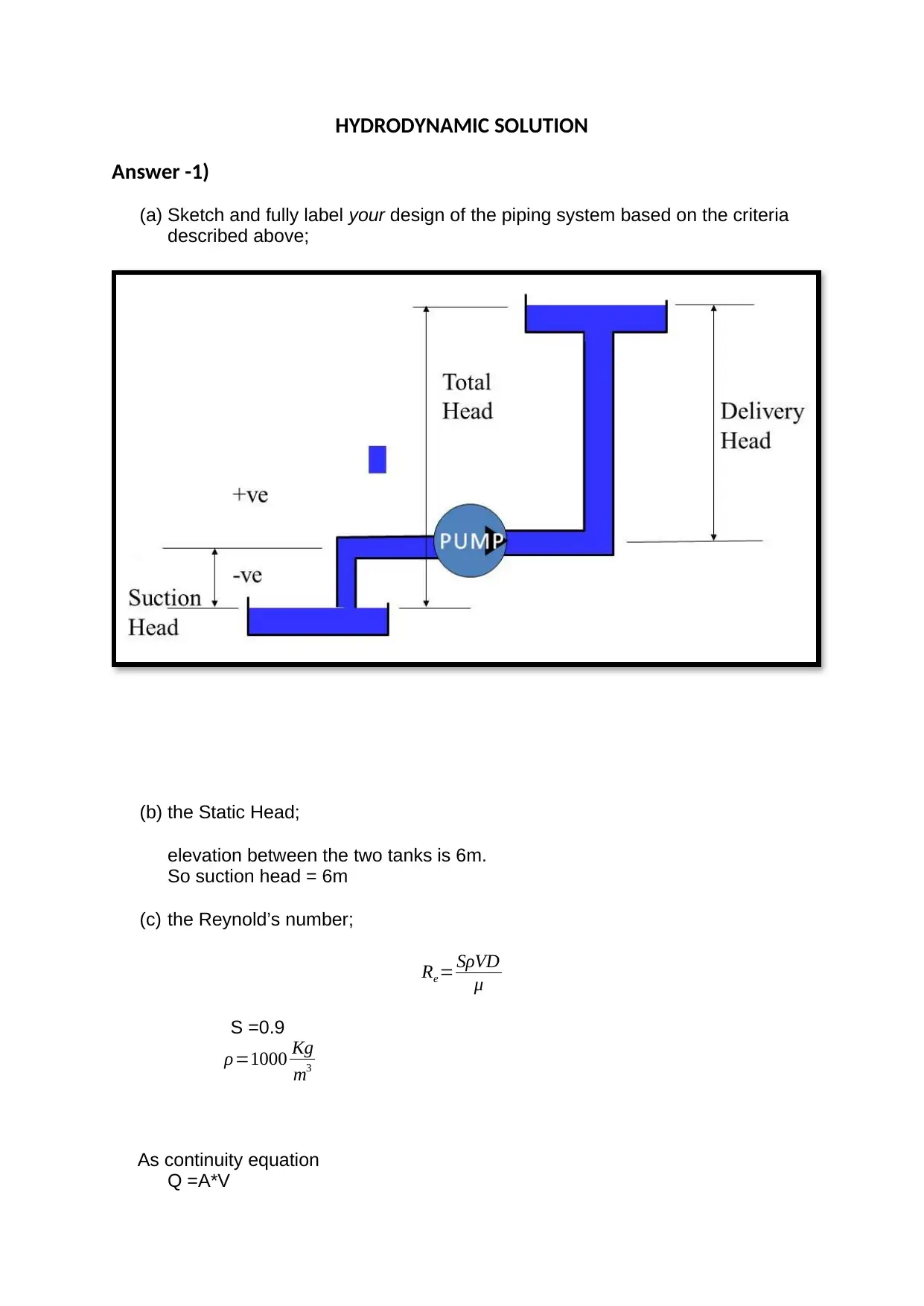
Answer -1)
(a) Sketch and fully label your design of the piping system based on the criteria
described above;
(b) the Static Head;
elevation between the two tanks is 6m.
So suction head = 6m
(c) the Reynold’s number;
Re= SρVD
μ
S =0.9
ρ=1000 Kg
m3
As continuity equation
Q =A*V

Q =2L/s
A=π r2
2
1000 = π∗( 0.01 ) 2
4 ∗V
So V =0.398 m/s
μ=0.005 Pas
Put all values we get ,
Re= 0.9∗1000∗0.398∗80
0.05∗1000
Re=5731.2
(d) the relative roughness of the pipe;
RR= D
ϵ
RR= 80
0.045
RR=1777.8
(e) the friction factor (using the Moody formula);
f = 0.316
Re
1
4
f = 0.316
(5731.2)
1
4
f =0.0363

(f) the total K factor for the fittings;
As k factor is given for all different condition
So total k factor = 0.5+1+0.2+6+ (15*0.03)+(4*0.6)
= 10.55
(g) the total head loss for pipe and fittings;
hl =10.55∗v2
2∗g
hl =10.55∗0.3982
2∗9.81
h¿=0.851 m
(h) the Dynamic Head;
hd= P2−P1
ρg
hd=5.81 m
(i) the System Head;
hsys=hd +hs
hsys=6+5.81
hsys=11.81 m
(j) the System Head Equation in terms of the volumetric flow rate
h= P
ρg + Q2
2 A2 g +C
(k) the Fluid Power;

FP=S ρghQ
FP= 0.9∗1000∗9.81∗11.81∗2
1000
FP=0.117 KW
(l) the Pump shaft Power, given that it has an efficiency of 72% at the given flow
rate.
eff = SP
FP
0.72= SP
117
SP=84.24 W
Answer 2

(a) the total head loss in the system;
h¿= 4 f l1 v1
2
2 g d1
+ 4 f l2 v2
2
2 g d2
+ 4 f l3 v3
2
2 g d3
Neglecting all minor losses
From here we calculate
h= P
S ρg + v1
2
2 g
20= 50
0.78∗9.81 + v1
2
2∗9.81
V1 = 9.47 m/s
From continuity equation
Q= A1∗V 1= A2∗V 2= A3∗V 3
A1∗V 1=A2∗V 2
302∗9.47=252∗V 2
V2 = 13.63 m/s

A3∗V 3= A2∗V 2
202∗V 3=252∗13.63
V3 = 21.3 m/s
Re= SρVD
μ
Re= 0.78∗1000∗9.47∗30
0.002∗1000
Re=110799
f = 0.316
Re
1
4
f = 0.316
(110799)
1
4
f =0.173
Put all values we get
h¿= 4∗0.173∗50∗9.472
2∗9.81∗0.03 + 4∗0.173∗50∗13.632
2∗9.81∗0.025 + 4∗0.173∗20∗21.32
2∗9.81∗0.02
h¿=3.434 m
(b) the total equivalent length based on the 25mm diameter pipe;
L
D5 = L1
D5
1
+ L2
D5
2
+ L3
D5
3
L
0.0255 = 50
0.035 + 50
0.0255 + 20
0.025
L=131.12 m

(c) the volumetric flow rate (using an initial trial friction factor value f = 0.02 and
performing 3 trials).
Q= A1 V 1
Put values we get
Q= π∗0.032∗9.47
4
Q=6.69 L/ s
Answer 3)
(a) the flow velocity in pipes A and D;
As Va =Vd
Qa= Aa∗V a
75
1000 = π∗0.22∗V a
4
Put values
Va =Vd = 2.387 m/s
(b) the total head loss in pipes A and D;
hla= 4 f la va
2
2 g da
hla= 4∗0.025∗120∗2.3872
2∗9.81∗0.2
hla=4.356 m
hld = 4 f ld vd
2
2 g dd

hld = 4∗0.025∗180∗2.3872
2∗9.81∗0.2
hld =6.534 m
(c) an algebraic expression for the head loss in pipes B and C in terms of their
pipe velocities (Hint: use D’Arcy equation);
hlb= 4 f lb vb
2
2 g db
hlb= 4∗0.025∗40∗vb
2
2∗9.81∗0.12
hlb=0.424 vb
2
hlc = 4 f lc vc
2
2 g dc
hlc = 4∗0.025∗8 0∗vc
2
2∗9.81∗0.08
hlc =1.274 vc
2
(d) an algebraic expression for the volumetric flow rate in terms of the pipe flow
velocities of B and C (Hint: use Continuity equation);
Qb= Ab V b
Qb= π∗0.122∗V b
4
Qb=0.011V b
Similarly
Qc= π∗0.082∗V c
4
Qc=0.0064 V c

(e) the flow velocities in pipes of B and C;
For paraller pipes
Qa=Qc+Qb
hlb=hlc Put all values we get
0.424 vb
2=1.274 vc
2
vb
vc
=1.536
75
1000 =Qc+Qb
75
1000 =0.011V b+0.0064 V c
75
1000 =0.023 V c
V c=3.219 m/s
V b =4.945 m/s
(f) the volumetric flow rates through pipes B and C;
Qa=Qc+Qb
75
1000 =0.011V b+0.0064 V c
75
1000 =0.011∗4.945+0.0064∗3.219
Qb=54.4 L
s
Qc=20.6 L
s
(g) the head loss through pipe B or C (Should be the same);
hlb=0.424 vb
2
hlb=0.424∗4.9452

hlb=hlc=10.368
(h) the overall head loss for the pipe network;
hl =hla+hlb+hlc +hld
hl =4.356+10.368+10.368+ 6.534
hl =31.62m
(i) the mass flow rate;
m=S∗ρ∗Q
m= 0.78∗1000∗75
1000
m = 58.5 Kg /s
(j) the overall Fluid Power required to maintain flow in the network;
FP=S ρghQ
FP= 0.78∗1000∗9.81∗31.62∗75
1000
FP=18.14 KW
(k) the Pump shaft Power, given that it has an efficiency of 75% at the given flow
rate.
eff = SP
FP
0.75= SP
18.14
SP=13.69 k W

Answer 4)
determine the power absorbed due to viscous friction
P= 2 πNT
60
T = W∗d
2
W =τ∗A
τ = μ∗v
y
A=π dl
A=π
75
1000∗150
1000
A=0.0353 m2
v= π∗d∗N
60
v=
π∗75
1000 ∗3000
60
v=11.775 m
s
τ = μ∗v
y
τ = 0.38∗11.775
0.1 ∗1000
τ =44.74 Kpa
W =τ∗A
W =44.74∗0.0353
W =1.58 K N
Put all the above values we get
T = W∗d
2

T = 1.58∗75
2
T =59.2 Nm
P= 2 π∗3000∗59.2
60
P=18.6 K W
Answer 5)
calculate the hydraulic radius ‘R” and hence determine the minimum angle of
inclination (in degrees) of the channel
h =300 mm
r =400 mm
hydraulic radius
R= A
Pw
α =2 cos−1 (1− h
r ¿)¿
α =2 cos−1 (1− 300
400 ¿)¿
α=151.04 °
Pw=α∗r Wetted perimeter
h r
α

Pw=
151.04∗π
180 ∗400
1000
Pw=1.054 m
A=r2 ¿ ¿ Constructed area
A=4002 ¿ ¿
A=0.172 m2
Now hydraulic radius ‘R
R= A
Pw
R= 0.172
1.054
R=163.27 mm