Data Analysis and Forecasting for Turkey's Population and Vehicles

This study report demonstrates worthwhile data interpretation and forecast methods that aid in anticipating the significance of Turkey's overall population as well as vehicles used in urban markets. The regression evaluation principle is useful in identifying the actual association between variables which facilitates efficient decision-making.

Individual assessment
(Data Analysis and
Forecasting)
ABSTRACT
This study report demonstrates worthwhile data interpretation and forecast methods that aid in
anticipating the significance of Turkey's overall population as well as vehicles used in urban

markets. The regression evaluation principle is useful in identifying the actual association
between variables which facilitates efficient decision-making.

Contents
ABSTRACT.....................................................................................................................................2
INTRODUCTION...........................................................................................................................4
MAIN BODY...................................................................................................................................4
a. Scatter graphs......................................................................................................................4
b. Equation with relation to regression line............................................................................7
c. Scatter graphs......................................................................................................................7
d. Equation of regression line.................................................................................................9
e. Two regression equations...................................................................................................9
f. Future values by using liner regression equations............................................................10
CONCLUSION..............................................................................................................................10
REFERENCES..............................................................................................................................11

INTRODUCTION
Data analysis relates to the method of acquiring useful information relevant to a given task or
triggering within an entity and allowing accurate analysis to identify the major problems or some
other primary findings. Data analysis can also be useful in many ways for businesses working
with massive numbers, as it offers a summary about real activity events resulting in critical
decision making (Hackl, 2013). This also assists in creating realistic predictions of potential
opportunities and market outcomes which can be achieved by careful plan implementation.
Multiple graph as well as regression line measurements are shown in the study report.
Furthermore, the report also includes possible forecast with sufficient clarification for turkey
vehicles.
MAIN BODY
a. Scatter graphs
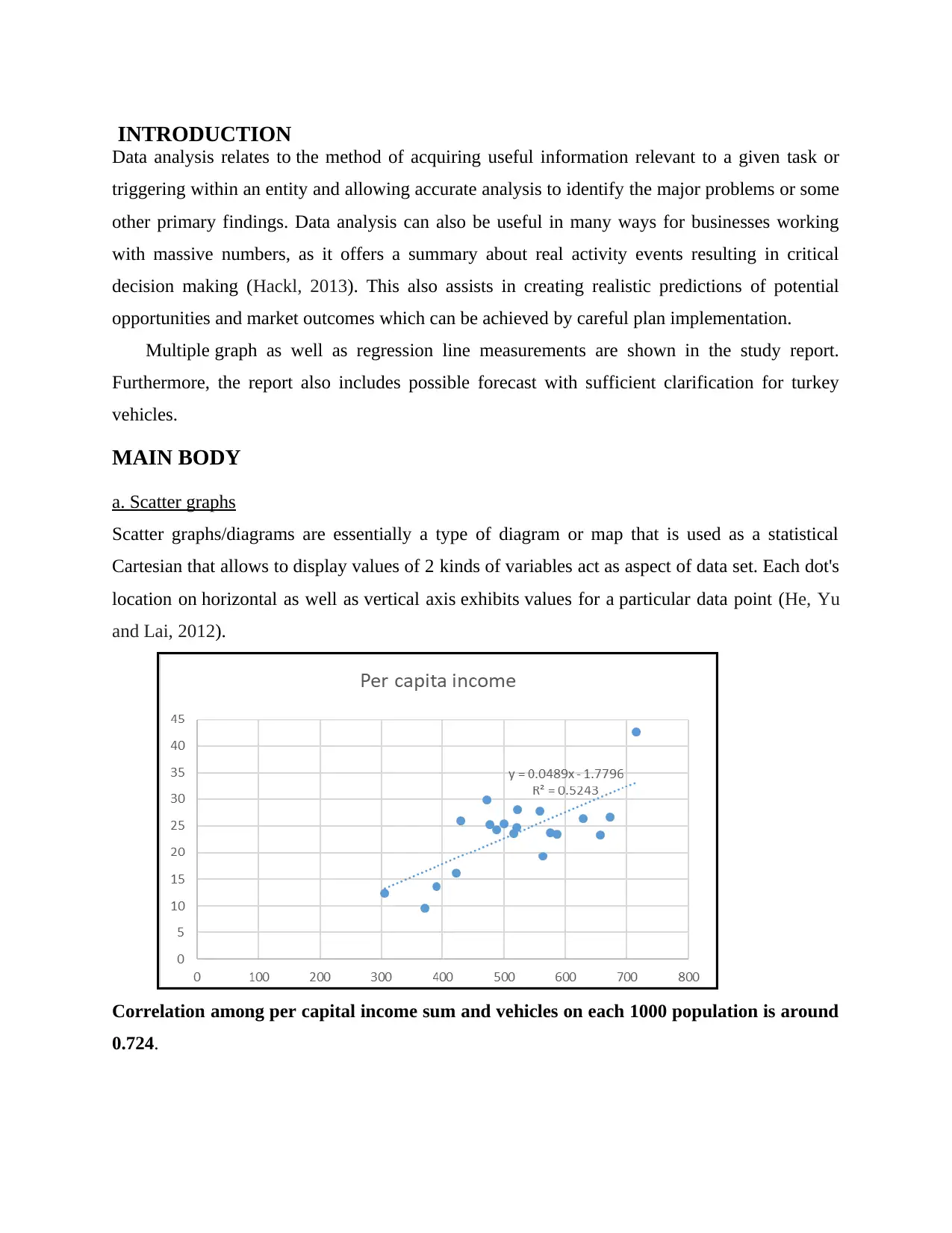
Scatter graphs/diagrams are essentially a type of diagram or map that is used as a statistical
Cartesian that allows to display values of 2 kinds of variables act as aspect of data set. Each dot's
location on horizontal as well as vertical axis exhibits values for a particular data point (He, Yu
and Lai, 2012).
Correlation among per capital income sum and vehicles on each 1000 population is around
0.724.

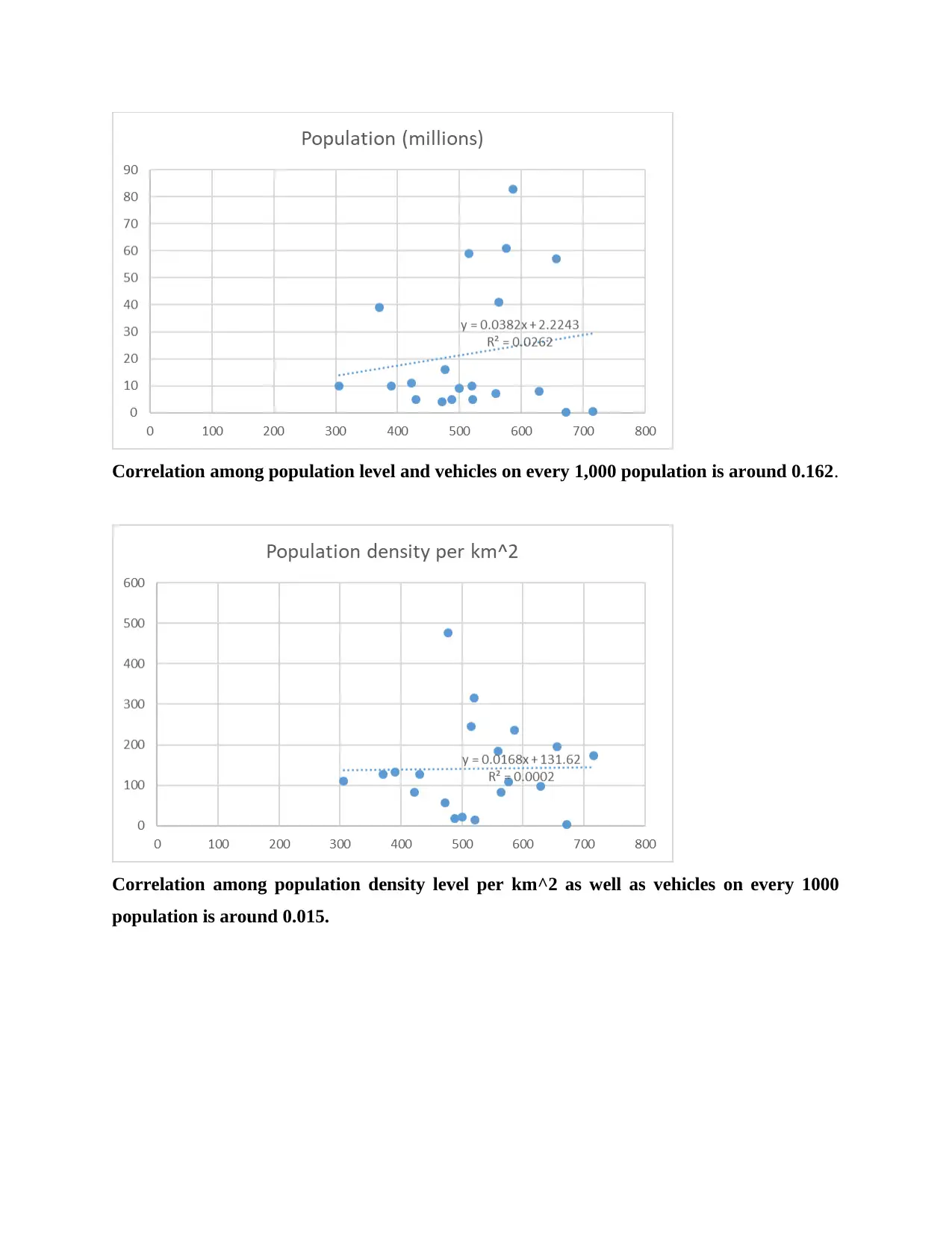
Correlation among population level and vehicles on every 1,000 population is around 0.162.
Correlation among population density level per km^2 as well as vehicles on every 1000
population is around 0.015.

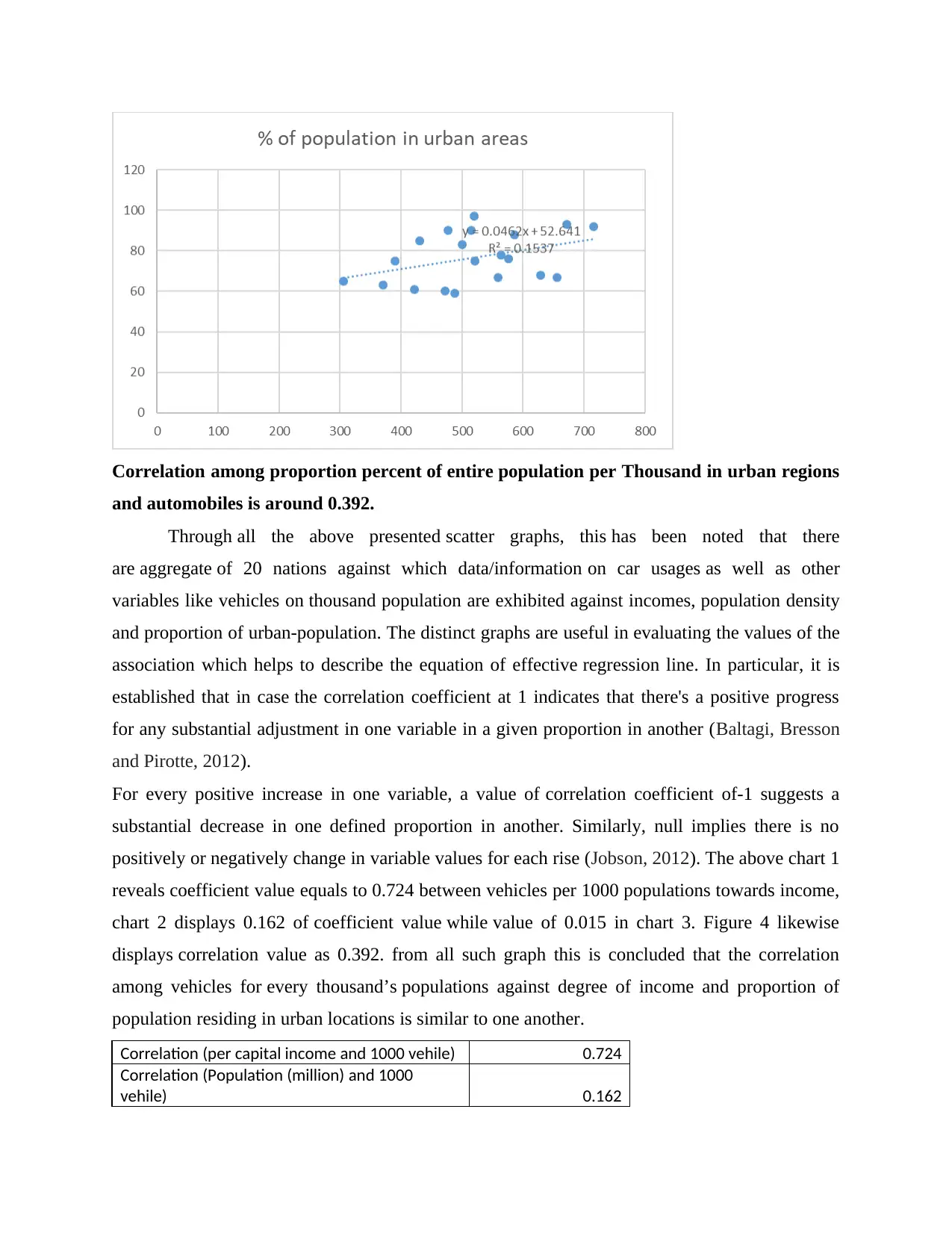
Correlation among proportion percent of entire population per Thousand in urban regions
and automobiles is around 0.392.
Through all the above presented scatter graphs, this has been noted that there
are aggregate of 20 nations against which data/information on car usages as well as other
variables like vehicles on thousand population are exhibited against incomes, population density
and proportion of urban-population. The distinct graphs are useful in evaluating the values of the
association which helps to describe the equation of effective regression line. In particular, it is
established that in case the correlation coefficient at 1 indicates that there's a positive progress
for any substantial adjustment in one variable in a given proportion in another (Baltagi, Bresson
and Pirotte, 2012).
For every positive increase in one variable, a value of correlation coefficient of-1 suggests a
substantial decrease in one defined proportion in another. Similarly, null implies there is no
positively or negatively change in variable values for each rise (Jobson, 2012). The above chart 1
reveals coefficient value equals to 0.724 between vehicles per 1000 populations towards income,
chart 2 displays 0.162 of coefficient value while value of 0.015 in chart 3. Figure 4 likewise
displays correlation value as 0.392. from all such graph this is concluded that the correlation
among vehicles for every thousand’s populations against degree of income and proportion of
population residing in urban locations is similar to one another.
Correlation (per capital income and 1000 vehile) 0.724
Correlation (Population (million) and 1000
vehile) 0.162

Correlation (Population density per km^2 and
vehicles per 1000 population) 0.015
Correlation (Percentage of population in urban
areas and vehicles per 1000 population) 0.392
b. Equation with relation to regression line
From the displayed graph above, 2 dependent factors such as income scale and actual proportion
of living regions of populations are found to be more associated with independent variable
Vehicles on every 1000 population. Of these factors’ liner equation is as follows:
Specific formula of the equation is :- y = a + bx, here in Y denotes a depended factor/variable
whereas x points out towards the value of a independent variable. In order to assess values of a &
b.
For aggregate population residing in the urban areas as well as Vehicles usage in per
thousand people population under liner equation, as follows:
Y= 0.0462x + 52.641
R2 = 0.01537
Furthermore, equation with respect to regression line relating to Vehicles
per thousand population as well as population's income level are as follows:
Y= 0.0489 x -1.7796
R2 = 0.5243
c. Scatter graphs

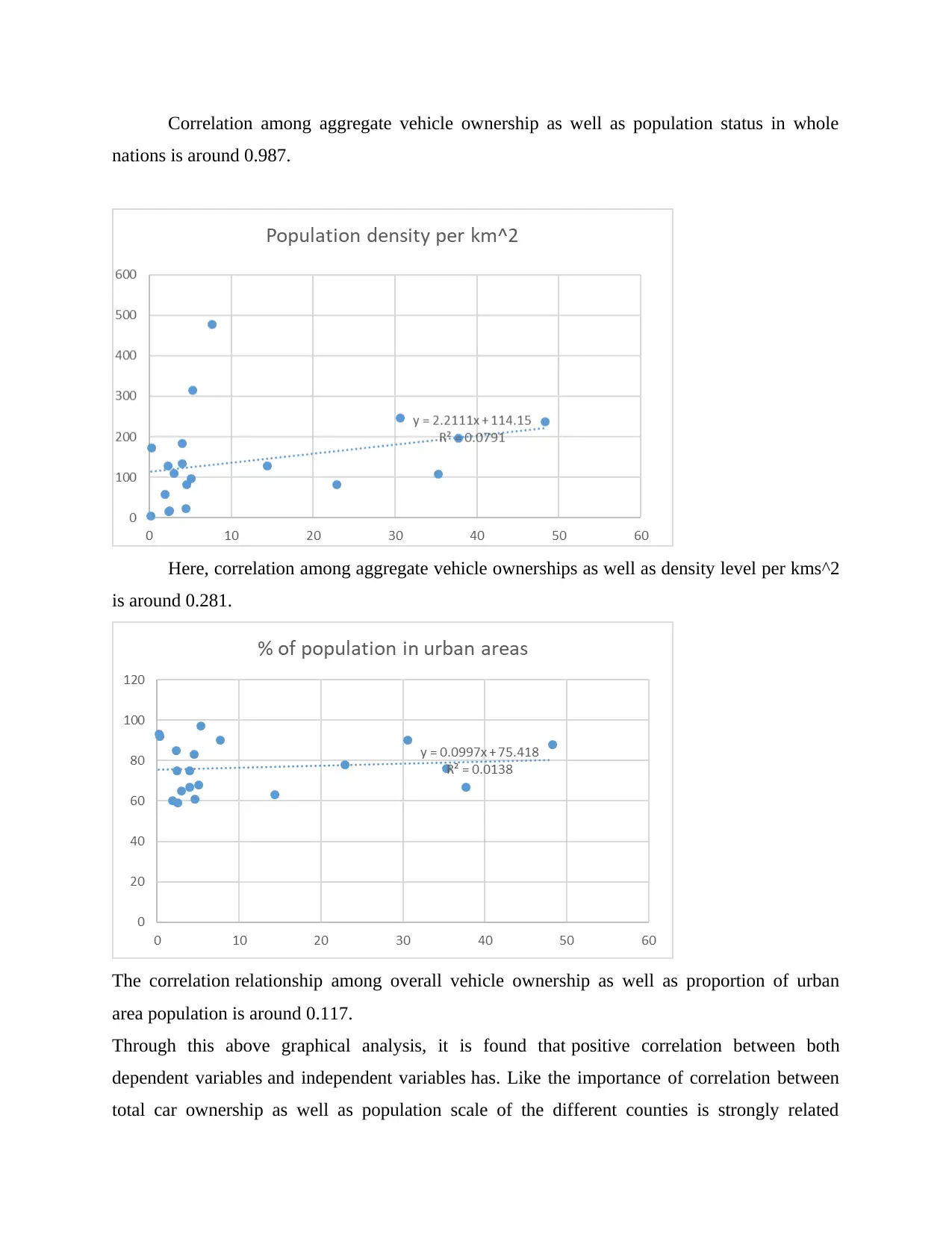
Correlation among aggregate vehicle ownership as well as population status in whole
nations is around 0.987.
Here, correlation among aggregate vehicle ownerships as well as density level per kms^2
is around 0.281.
The correlation relationship among overall vehicle ownership as well as proportion of urban
area population is around 0.117.
Through this above graphical analysis, it is found that positive correlation between both
dependent variables and independent variables has. Like the importance of correlation between
total car ownership as well as population scale of the different counties is strongly related

to standard correlation significance. Thus, in meantime, 0.987 is perceived to be nearest value to
a positive correlation and that can be utilized to assess regression value of such variables.
d. Equation of regression line
Linear regression evaluates an estimate that greatly decreases the distance over the related lines
from all datasets. Structurally, the evaluation of common minus squares decreases the overall
squared residuals. Therefore, if the deviations between the observed values as well as model's
predicted values are small and unbiased a model will match well with the results (Qin, Wang and
Sun, 2014). R-squared relates to quantitative measure of how close the direction of regression
built with the results is. It is also identified as the variable of decision, or numerous decision
variables for a number of regressions. Since R-squared value is low but still has statistically
important determinants, it is therefore possible to make critical conclusions about whether
changes in a predictor values are associated with changes in outcome values (Montgomery,
Jennings and Kulahci, 2015). Apart of R-squared, the related coefficients also represent the mean
deviation in response per one division of move in predictor while holding those determinants
static in this model. Of course, that kind of information can be extremely useful.
through the aforementioned scatter plot, this has been quantified that most substantial
value coefficient in whole nations is among overall vehicle ownership versus population levels,
hence liner regression equation in this regard is as pursues:
‘y’ = 1.6789 x + 2.1399
R2 = 0.09744
At other hand, the equation of regression with respect to aggregate vehicle ownerships variables
as well as population density residing in different nations per ^2 km, as follows:
Y= 2.2111x + 114.15
R2 = 0.0791
e. Two regression equations
From the various regression values estimated above, most relevant liner equation with respect
to the car industry is described below:
 Vehicles at 1000 population as well as population's income is as below:
Y= 0.0489x-1.7796
R2 = 0.5243
 Overall ownership of vehicles as well as population size per ^2 km

Y= 2.2111x + 114.15
R2 = 0.0791
These 2 equations of liner-regression values could be an absolutely efficient mathematical tool
that could be used to generate insights into consumer preferences, a marketplace understanding
which influences feasibility. Linear regressions can be employed in automotive companies to
assess trends and to make forecasts or speculations. Negative coefficients could therefore be
interpreted as negative or inverse relationship with coefficient of regression so that it can be
presumed to be a beneficial result (Antoniou and Yannis, 2013). The primary component for any
mathematical model is correct understanding of the subject and its activity in the marketplace.
The advantage of a linear regression is that it lets us capture each marketing strategy's distinct
factors along with tracking the variables which could impact the revenues. In real-life cases,
there are often advertising campaigns that run for a car manufacturer during same time period
that is successful in deciding company's total revenue profit in the foreseeable future. Regression
modelling will give an analytical insight to each corporation’s management. Study of regression
leads the way towards better and more educated decisions by turning the huge amount of raw
details into credible information. This doesn't say that the assessment process always stops
managers ' creative inventions. This approach serves as a valuable tool for testing a concept
before immersion in organization success. This improves market efficiency by emphasizing
places where organizational productivity and profits have the substantial impact.
f. Future values by using liner regression equations.
As per the assessed values through liner regression equation calculations as shown in section
d and b this has been forecasted that vehicle on per 1000 people within the turkey will be on an
average 518. Also, aggregate level of vehicles’ ownership will reach to a level of around 11.85
within turkey.
CONCLUSION
It has been asserted from the above study that process of data analysis is extremely useful in
evaluating the functional value for potential usage and also supports successful efforts to directly
improve overall efficiency. Additionally, the use of various statistical methods and techniques
such as correlation as well as regression is useful in determining future values.

REFERENCES
Books and Journals
Hackl, P. ed., 2013. Statistical analysis and forecasting of economic structural change. Springer
Science & Business Media.
He, K., Yu, L. and Lai, K.K., 2012. Crude oil price analysis and forecasting using wavelet
decomposed ensemble model. Energy, 46(1), pp.564-574.
Baltagi, B.H., Bresson, G. and Pirotte, A., 2012. Forecasting with spatial panel
data. Computational Statistics & Data Analysis, 56(11), pp.3381-3397.
Qin, S., Liu, F., Wang, J. and Sun, B., 2014. Analysis and forecasting of the particulate matter
(PM) concentration levels over four major cities of China using hybrid
models. Atmospheric Environment, 98, pp.665-675.
Antoniou, C. and Yannis, G., 2013. State-space based analysis and forecasting of macroscopic
road safety trends in Greece. Accident Analysis & Prevention, 60, pp.268-276.
Montgomery, D.C., Jennings, C.L. and Kulahci, M., 2015. Introduction to time series analysis
and forecasting. John Wiley & Sons.
Jobson, J.D., 2012. Applied multivariate data analysis: regression and experimental design.
Springer Science & Business Media.