Individual Report: Descriptive Analysis Techniques for Data Analysis

This individual report provides a comprehensive overview of descriptive analysis techniques applied to a dataset of phone calls. The report begins with the creation of a table to organize the data and follows with graphical representations using column and line charts to visualize call patterns over a p...Read More

INDIVIDUAL REPORT

TABLE OF CONTENTS
TABLE OF CONTENTS................................................................................................................2
EXECUTIVE SUMMARY.............................................................................................................1
REFERENCES................................................................................................................................2

INTRODUTION
Descriptive analysis includes techniques which includes the tables of mean and for
quantities, measuring the dispersion like the variance of the standard deviation and the cross
tabulations or the cross tabs which is used for examining many disparate hypothesis. The report
will provide about descriptive analysis techniques for evaluating data.
TASK
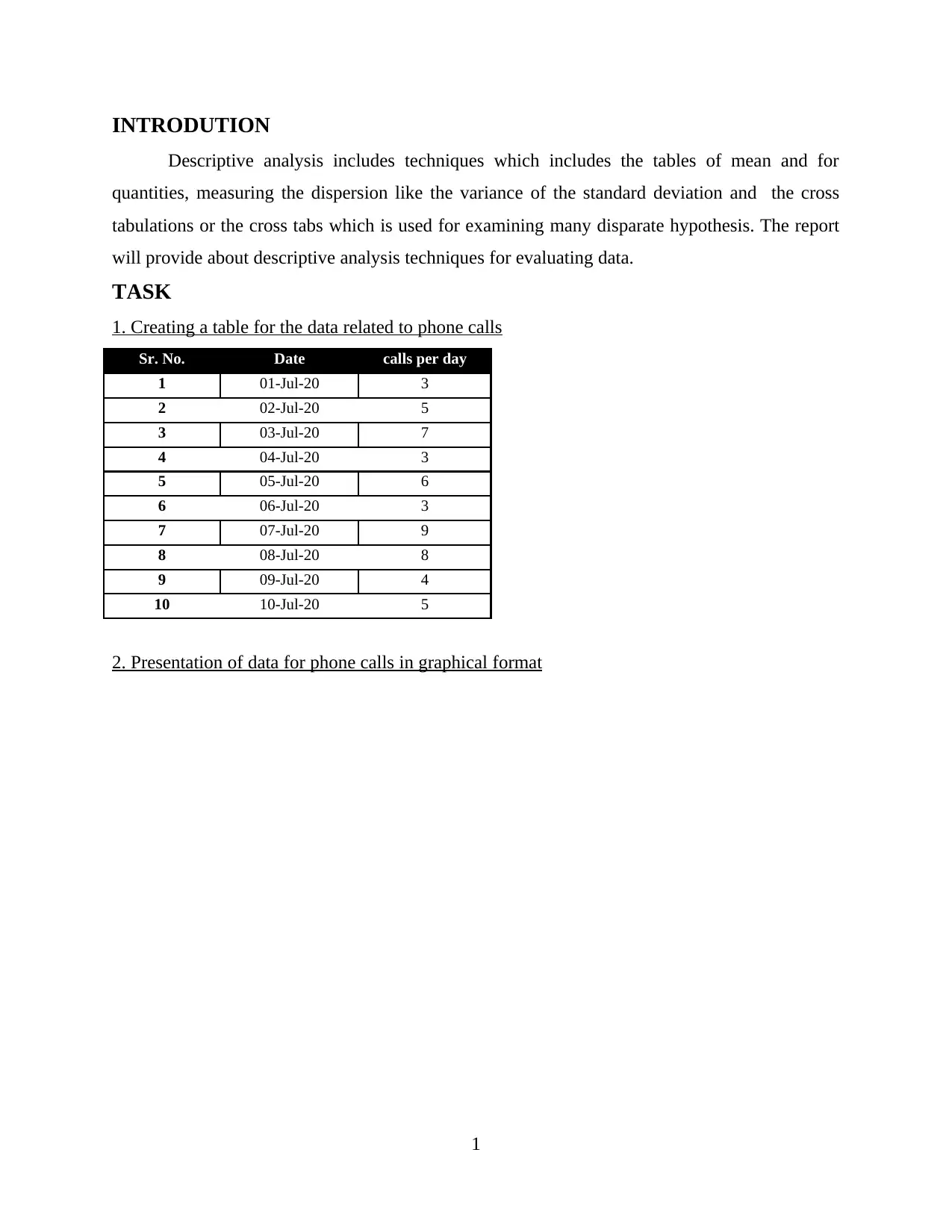
1. Creating a table for the data related to phone calls
Sr. No. Date calls per day
1 01-Jul-20 3
2 02-Jul-20 5
3 03-Jul-20 7
4 04-Jul-20 3
5 05-Jul-20 6
6 06-Jul-20 3
7 07-Jul-20 9
8 08-Jul-20 8
9 09-Jul-20 4
10 10-Jul-20 5
2. Presentation of data for phone calls in graphical format
1

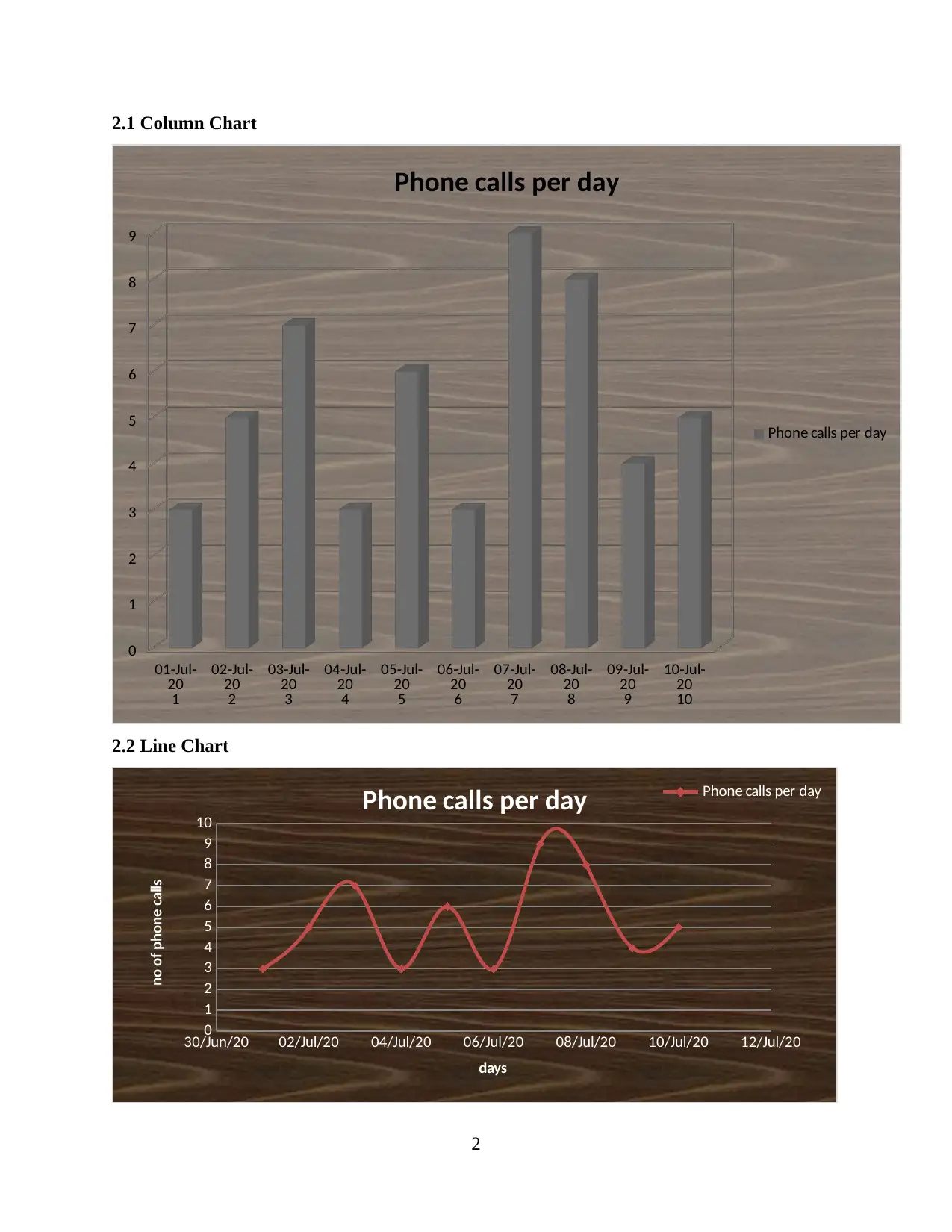
2.1 Column Chart
01-Jul-
20 02-Jul-
20 03-Jul-
20 04-Jul-
20 05-Jul-
20 06-Jul-
20 07-Jul-
20 08-Jul-
20 09-Jul-
20 10-Jul-
20
1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
Phone calls per day
Phone calls per day
2.2 Line Chart
30/Jun/20 02/Jul/20 04/Jul/20 06/Jul/20 08/Jul/20 10/Jul/20 12/Jul/20
0
1
2
3
4
5
6
7
8
9
10
Phone calls per day Phone calls per day
days
no of phone calls
2

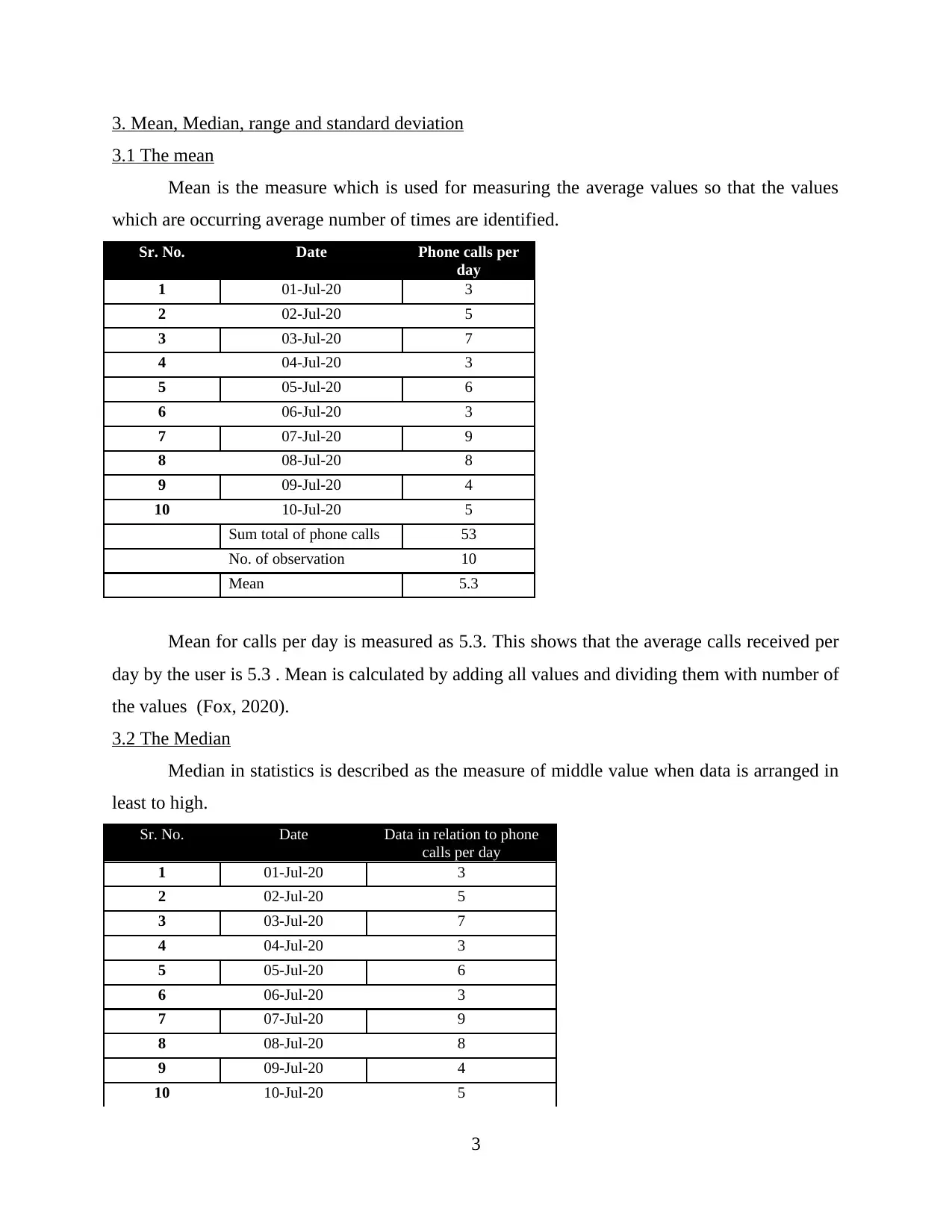
3. Mean, Median, range and standard deviation
3.1 The mean
Mean is the measure which is used for measuring the average values so that the values
which are occurring average number of times are identified.
Sr. No. Date Phone calls per
day
1 01-Jul-20 3
2 02-Jul-20 5
3 03-Jul-20 7
4 04-Jul-20 3
5 05-Jul-20 6
6 06-Jul-20 3
7 07-Jul-20 9
8 08-Jul-20 8
9 09-Jul-20 4
10 10-Jul-20 5
Sum total of phone calls 53
No. of observation 10
Mean 5.3
Mean for calls per day is measured as 5.3. This shows that the average calls received per
day by the user is 5.3 . Mean is calculated by adding all values and dividing them with number of
the values (Fox, 2020).
3.2 The Median
Median in statistics is described as the measure of middle value when data is arranged in
least to high.
Sr. No. Date Data in relation to phone
calls per day
1 01-Jul-20 3
2 02-Jul-20 5
3 03-Jul-20 7
4 04-Jul-20 3
5 05-Jul-20 6
6 06-Jul-20 3
7 07-Jul-20 9
8 08-Jul-20 8
9 09-Jul-20 4
10 10-Jul-20 5
3

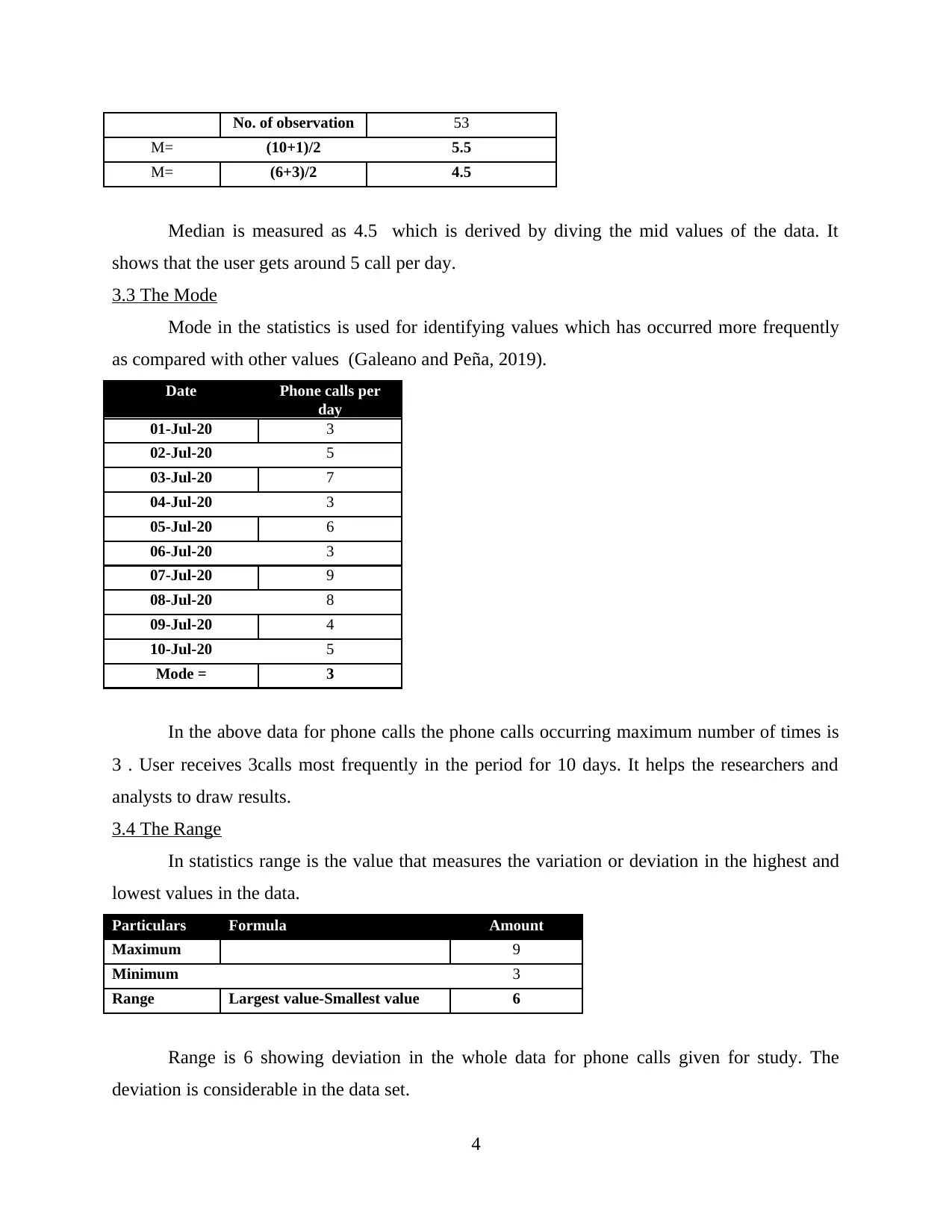
No. of observation 53
M= (10+1)/2 5.5
M= (6+3)/2 4.5
Median is measured as 4.5 which is derived by diving the mid values of the data. It
shows that the user gets around 5 call per day.
3.3 The Mode
Mode in the statistics is used for identifying values which has occurred more frequently
as compared with other values (Galeano and Peña, 2019).
Date Phone calls per
day
01-Jul-20 3
02-Jul-20 5
03-Jul-20 7
04-Jul-20 3
05-Jul-20 6
06-Jul-20 3
07-Jul-20 9
08-Jul-20 8
09-Jul-20 4
10-Jul-20 5
Mode = 3
In the above data for phone calls the phone calls occurring maximum number of times is
3 . User receives 3calls most frequently in the period for 10 days. It helps the researchers and
analysts to draw results.
3.4 The Range
In statistics range is the value that measures the variation or deviation in the highest and
lowest values in the data.
Particulars Formula Amount
Maximum 9
Minimum 3
Range Largest value-Smallest value 6
Range is 6 showing deviation in the whole data for phone calls given for study. The
deviation is considerable in the data set.
4

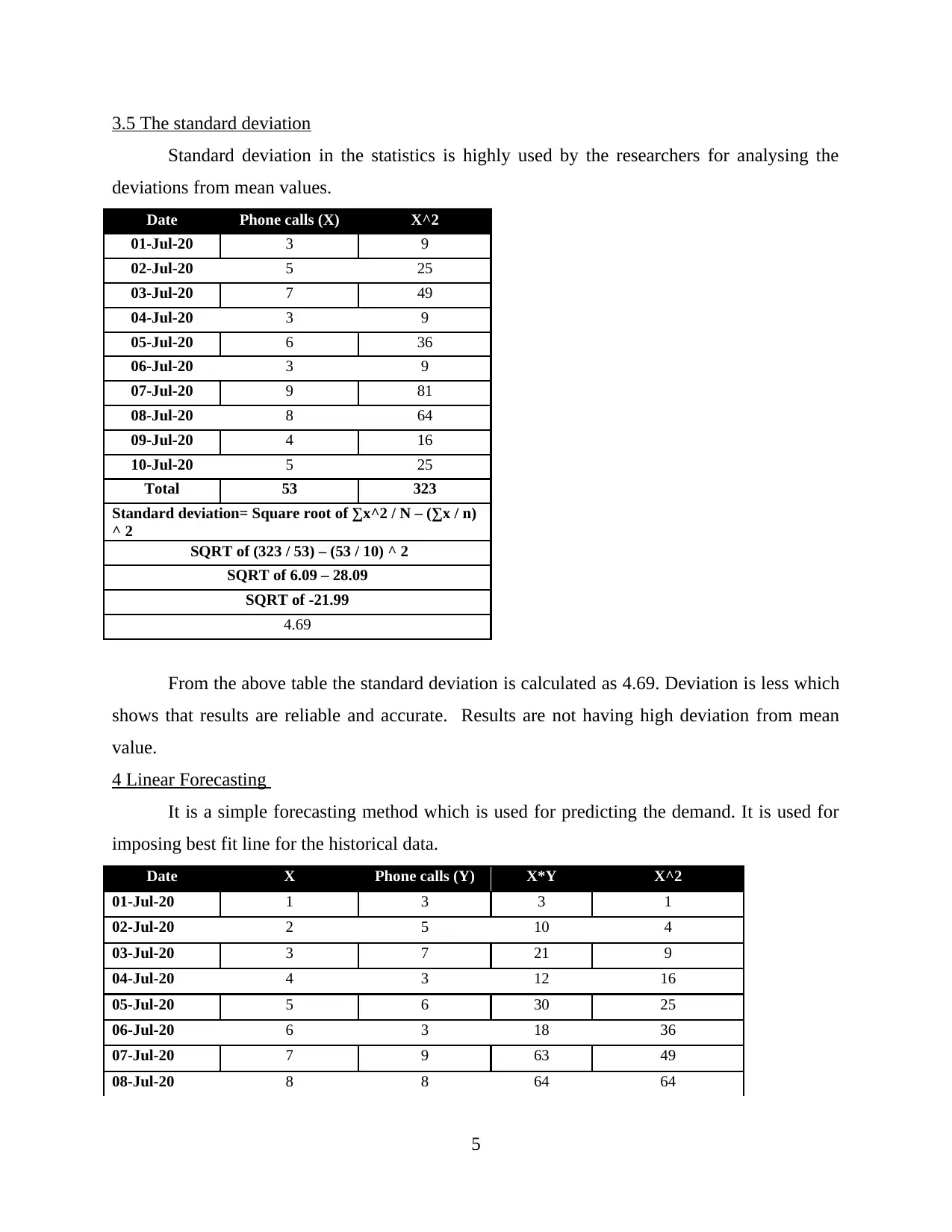
3.5 The standard deviation
Standard deviation in the statistics is highly used by the researchers for analysing the
deviations from mean values.
Date Phone calls (X) X^2
01-Jul-20 3 9
02-Jul-20 5 25
03-Jul-20 7 49
04-Jul-20 3 9
05-Jul-20 6 36
06-Jul-20 3 9
07-Jul-20 9 81
08-Jul-20 8 64
09-Jul-20 4 16
10-Jul-20 5 25
Total 53 323
Standard deviation= Square root of ∑x^2 / N – (∑x / n)
^ 2
SQRT of (323 / 53) – (53 / 10) ^ 2
SQRT of 6.09 – 28.09
SQRT of -21.99
4.69
From the above table the standard deviation is calculated as 4.69. Deviation is less which
shows that results are reliable and accurate. Results are not having high deviation from mean
value.
4 Linear Forecasting
It is a simple forecasting method which is used for predicting the demand. It is used for
imposing best fit line for the historical data.
Date X Phone calls (Y) X*Y X^2
01-Jul-20 1 3 3 1
02-Jul-20 2 5 10 4
03-Jul-20 3 7 21 9
04-Jul-20 4 3 12 16
05-Jul-20 5 6 30 25
06-Jul-20 6 3 18 36
07-Jul-20 7 9 63 49
08-Jul-20 8 8 64 64
5

09-Jul-20 9 4 36 81
10-Jul-20 10 5 50 100
Total 55 53 307 385
4.1 “m” value
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
m = 10 (307) - (53 * 55) / (10 * 385) – (55)^2
m = (3070 – 2915) / (3850 – 3025)
m = 155 / 825
m = 0.18
4.2 “c” value
c = Σy – m Σx / N
c = 53 – (0.18 * 55) / 10
c = (53 – 9.9) / 10
c = 43.1 / 10
c = 4.31
4.3 Day 12 Forecasting
Y = mX + c
= 0.18 * (12) + (4.31)
= 2.16 + 4.3
= 6.47 = 6 calls approx
4.4 Day 14 Forecasting
Y = mX + c
= 0.18 * (14) + (4.31)
= 2.52 + 4.31
= 6.83 = 7 calls approx
It could be analysed that using the linear forecasting, forecast for calls on 12th are forecasted
to be 6 calls and for 14th day forecasts are made as 7 calls per day. The forecasts for the future
dates are computed by deriving the values for m as well as c (Wildemuth, 2016). The method is
highly used by the researchers and also by companies for making forecasts for future incomes
and expenses.
6

CONCLUSION
Statistics play an important role in analysing the data. Using the different methods statistics
enable the researchers and analysts to come to more accurate and reliable results. Using
descriptive analysis accurate conclusions could be drawn in any research and for analysing the
data. The above report has provided brief outlook of the different methods such as mean, media
and mode.
7

REFERENCES
Books and Journals
Galeano, P. and Peña, D., 2019. Data science, big data and statistics. TEST, 28(2), pp.289-329.
Wildemuth, B.M., 2016. Descriptive statistics. Applications of Social Research Methods to
Questions in Information and Library Science, pp.338-47.
Fox, J., 2020. CRAN task view: Statistics for the social sciences.
8