Individual project on Catford Bridge in tabular

Individual project

Table of Contents
INTRODUCTION...........................................................................................................................1
MAIN BODY...................................................................................................................................1
1. Tabular representation of number of trains at Catford Bridge.................................................1
2. Graphical representation of observed data of Catford Bridge.................................................1
3. Calculation of various statistical tools of observed and collected data of Catford Bridge......3
4. Estimation of value of year 12 ans year 15 using linear forecasting model............................4
CONCLUSION................................................................................................................................5
REFERENCES................................................................................................................................7

INTRODUCTION
Observing the whole population and collecting specific data and analysing the data for
implementation of several statistical tools and determination of specific result of the data is
known as the whole statistical procedure of data analysis (Mendenhall, Sincich and Boudreau,
2016) . The present assignment shows number of trains at Catford Bridge in tabular as well as
graphical representation. It also shows calculation of descriptive statistical tools using collected
data of Catford Bridge. In addition, the assignment shows estimated value of Year 12 ans 15
using linear forecasting model.
MAIN BODY
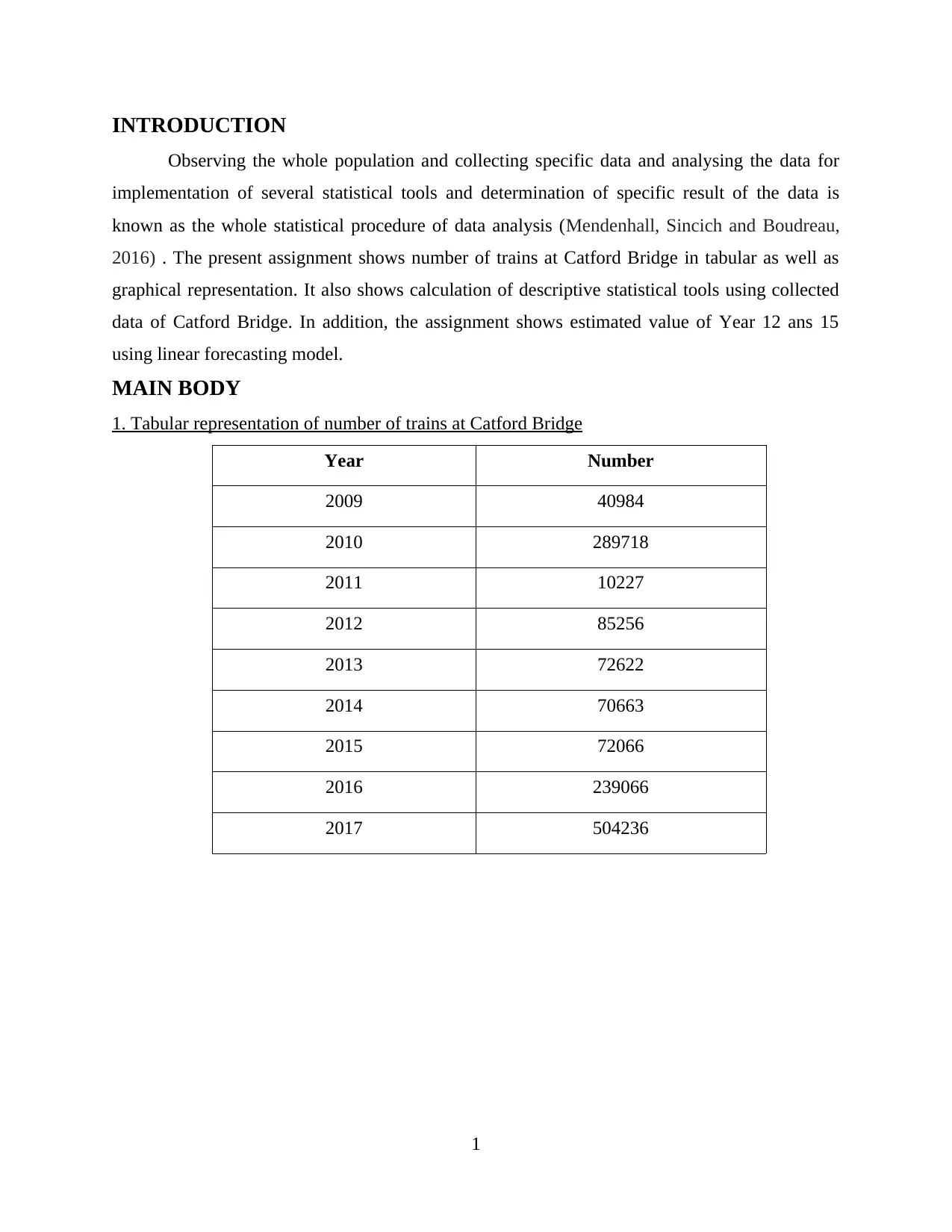
1. Tabular representation of number of trains at Catford Bridge
Year Number
2009 40984
2010 289718
2011 10227
2012 85256
2013 72622
2014 70663
2015 72066
2016 239066
2017 504236
1

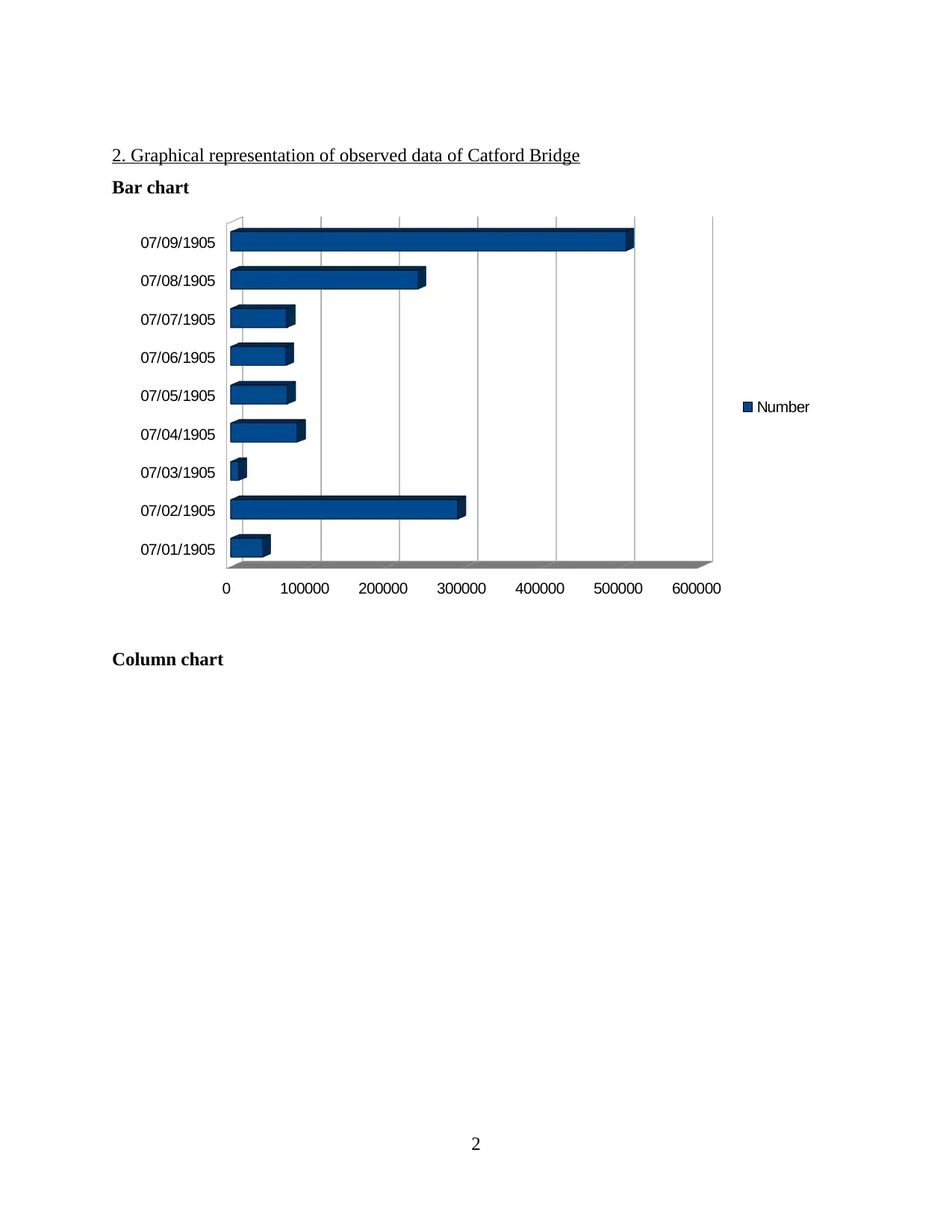
2. Graphical representation of observed data of Catford Bridge
Bar chart
Column chart
2
07/01/1905
07/02/1905
07/03/1905
07/04/1905
07/05/1905
07/06/1905
07/07/1905
07/08/1905
07/09/1905
0 100000 200000 300000 400000 500000 600000
Number

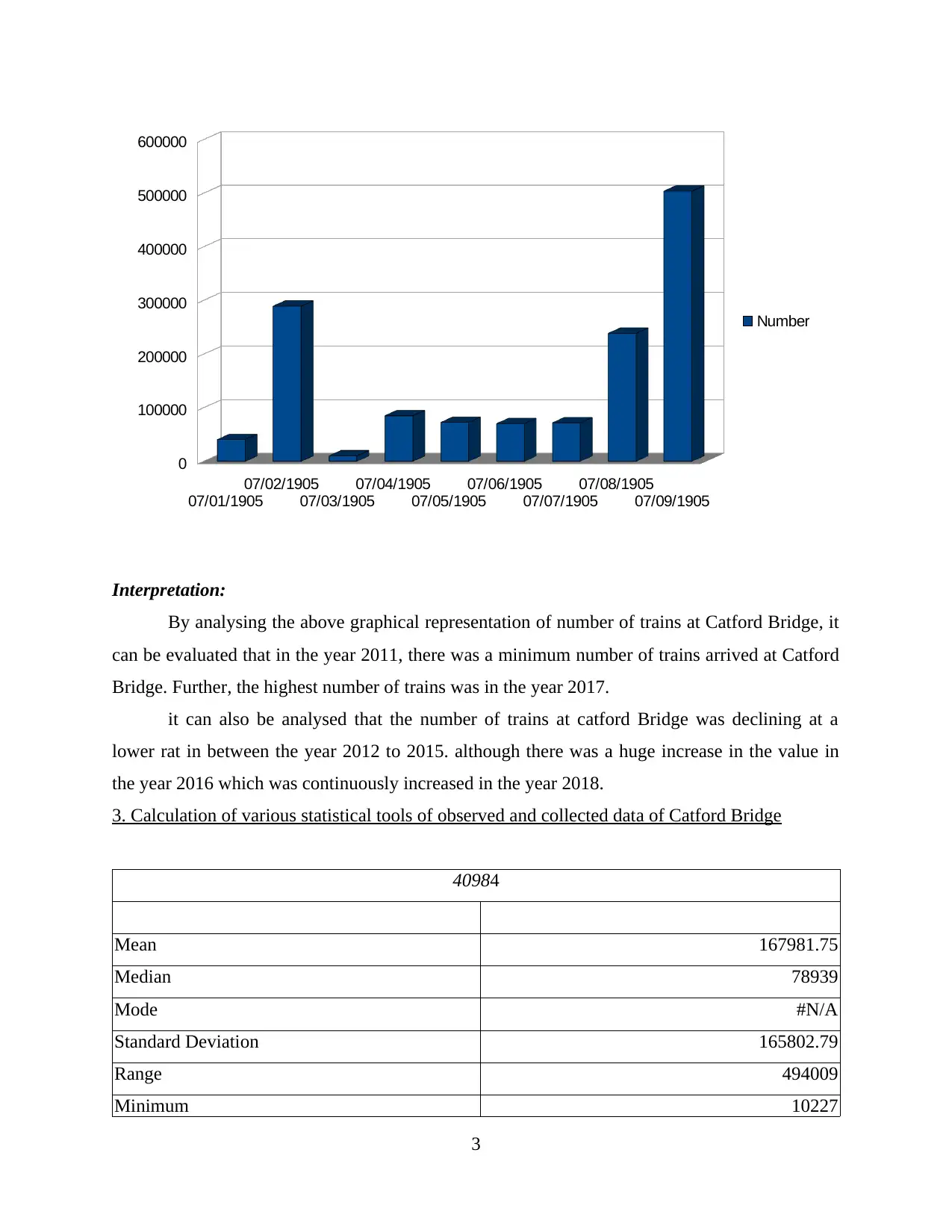
Interpretation:
By analysing the above graphical representation of number of trains at Catford Bridge, it
can be evaluated that in the year 2011, there was a minimum number of trains arrived at Catford
Bridge. Further, the highest number of trains was in the year 2017.
it can also be analysed that the number of trains at catford Bridge was declining at a
lower rat in between the year 2012 to 2015. although there was a huge increase in the value in
the year 2016 which was continuously increased in the year 2018.
3. Calculation of various statistical tools of observed and collected data of Catford Bridge
40984
Mean 167981.75
Median 78939
Mode #N/A
Standard Deviation 165802.79
Range 494009
Minimum 10227
3
07/01/1905
07/02/1905
07/03/1905
07/04/1905
07/05/1905
07/06/1905
07/07/1905
07/08/1905
07/09/1905
0
100000
200000
300000
400000
500000
600000
Number

Maximum 504236
The statistics provides various tools with the help of which the overall data can be
measured through which the actual result of the observed frequency can be determined easily.
Descriptive statistical tools that helps in evaluating various measurements of the observed
frequency (McCarthy and et.al., 2019) . This type of statistical tools are being used when the
there is a need of evaluating various measures of central tendency and determining effective
results from them as well. Mean, mode, median, kertosis, range, skewness, standard error,
standard variance, standard deviation, etc. are some of the key tools that are being used in
deriving several measures of central tendency.
Following are the essential statistical tools used for the measurement purpose:
 Mean : The mean can be defined as an average of several data of the entire observation.
It is part pf central tendency measurement. Therefore, this tool is used for the purpose of
determining average of the whole collected data. The mean or the average of the
observed frequency is 167981.75.
 Mode: It shows the data which has been occurred or included in the observation in
maximum time (Johnson and Bhattacharyya, 2018). As no data is being repeated in the
above data, mode of the above observed data is zero.
 Median: Median is the middle value of the data collected from the entire population. It
shows the middle most value of observation. Middle value of data related to Catford
Bridge is 78939
 Range: This tool is being used for the purpose of determining the mid point of maximum
and minimum value of the set of observation (Young and Wessnitzer, 2016) . Range of
the above observed data of Catford Bridge is 494009.
 Standard deviation: for the purpose of determining variation in two variables of set
data, the standard deviation tool is being used. In the present observed data related to
Catford Bridge is 165802.79
4

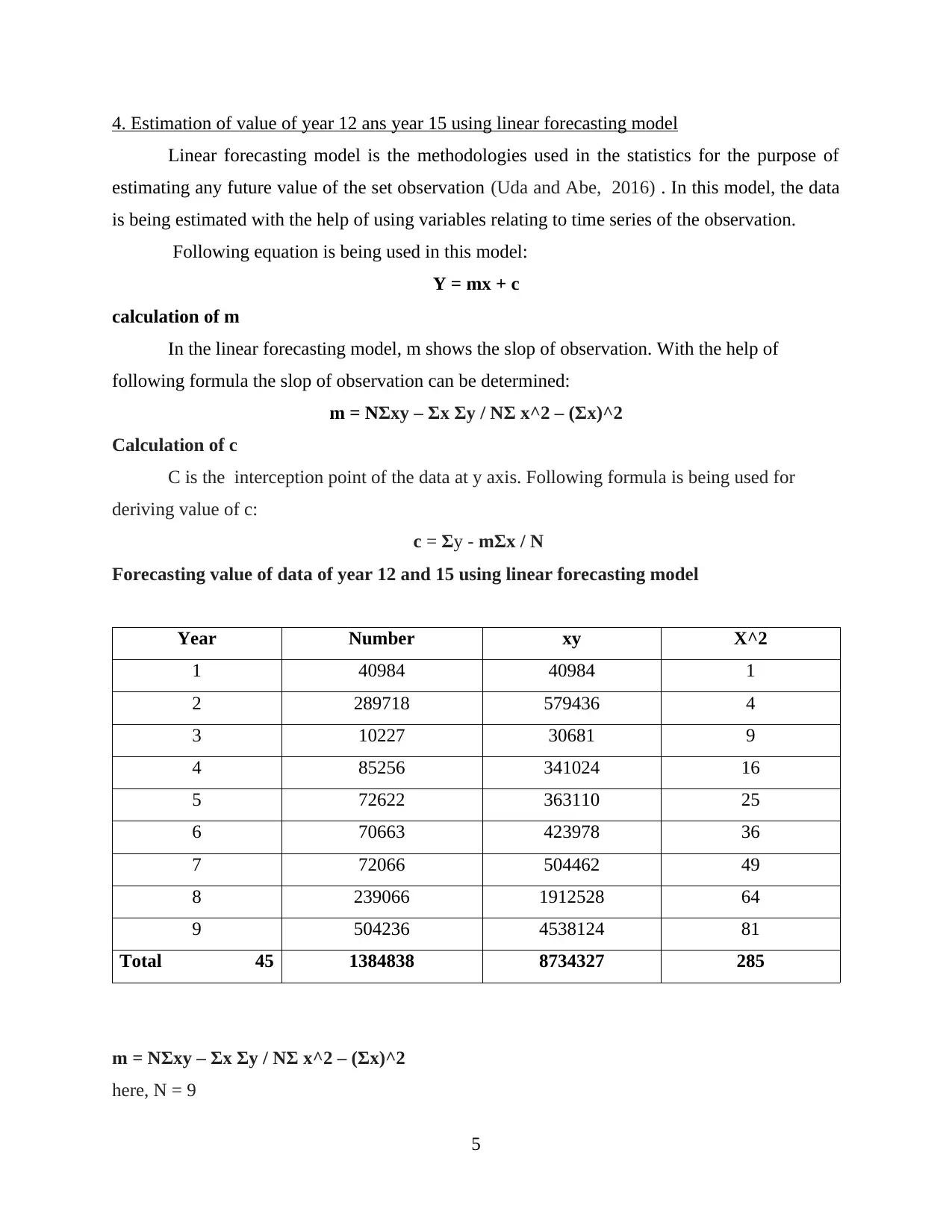
4. Estimation of value of year 12 ans year 15 using linear forecasting model
Linear forecasting model is the methodologies used in the statistics for the purpose of
estimating any future value of the set observation (Uda and Abe, 2016) . In this model, the data
is being estimated with the help of using variables relating to time series of the observation.
Following equation is being used in this model:
Y = mx + c
calculation of m
In the linear forecasting model, m shows the slop of observation. With the help of
following formula the slop of observation can be determined:
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
Calculation of c
C is the interception point of the data at y axis. Following formula is being used for
deriving value of c:
c = Σy - mΣx / N
Forecasting value of data of year 12 and 15 using linear forecasting model
Year Number xy X^2
1 40984 40984 1
2 289718 579436 4
3 10227 30681 9
4 85256 341024 16
5 72622 363110 25
6 70663 423978 36
7 72066 504462 49
8 239066 1912528 64
9 504236 4538124 81
Total 45 1384838 8734327 285
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
here, N = 9
5

Σx Σy = 45*1384838 = 62317710
Σx^2 = 285
(Σx)^ 2 = 45^ 2 = 2025
therefore, m = 9*1384838-6231770/9*285-2025
= −184877866.33
c = Σy - mΣx / N
here, Σy = 1384838
m = −184877866.33
Σx = 45
N = 9
hence, c = 1384838- (-184877866.33*45)/9
= 925774169.65
therfore, estimated value of year 12
Y = mX + c
= −184877866.33 * 12 + 925774169.65
= −1292760226.31
estimated value of year 15
Y = mX + c
= −184877866.33 * 15 + 925774169.65
= −1847393825.3
CONCLUSION
By analysing the above study of statistical project, it can be concluded that with the help
of various statistical methods and calculations, actual results of the observed data of entire
population can be generated. There are numerous tools that helps in determining various
measures of the statistical data. Statistics also provides various models that helps in determining
the estimated value of the overall set of data.
6

REFERENCES
Books and Journals
Mendenhall, W. M., Sincich, T. L. and Boudreau, N. S., 2016. Statistics for Engineering and the
Sciences, Student Solutions Manual. Chapman and Hall/CRC.
McCarthy, R.V. and et.al., 2019. What Do Descriptive Statistics Tell Us. In Applying Predictive
Analytics (pp. 57-87). Springer, Cham.
Young, J. and Wessnitzer, J., 2016. Descriptive statistics, graphs, and visualisation. In Modern
statistical methods for HCI (pp. 37-56). Springer, Cham.
Uda, T. and Abe, T., 2016. A Descriptive Statistics on Coworking Spaces in Japan. Available at
SSRN 2749515.
Johnson, R. A. and Bhattacharyya, G. K., 2018. Statistics: principles and methods. Wiley.
7