Individual Project: Data Analysis and Linear Forecasting Model Report
VerifiedAdded on 2023/01/07
|11
|1543
|38
Report
AI Summary
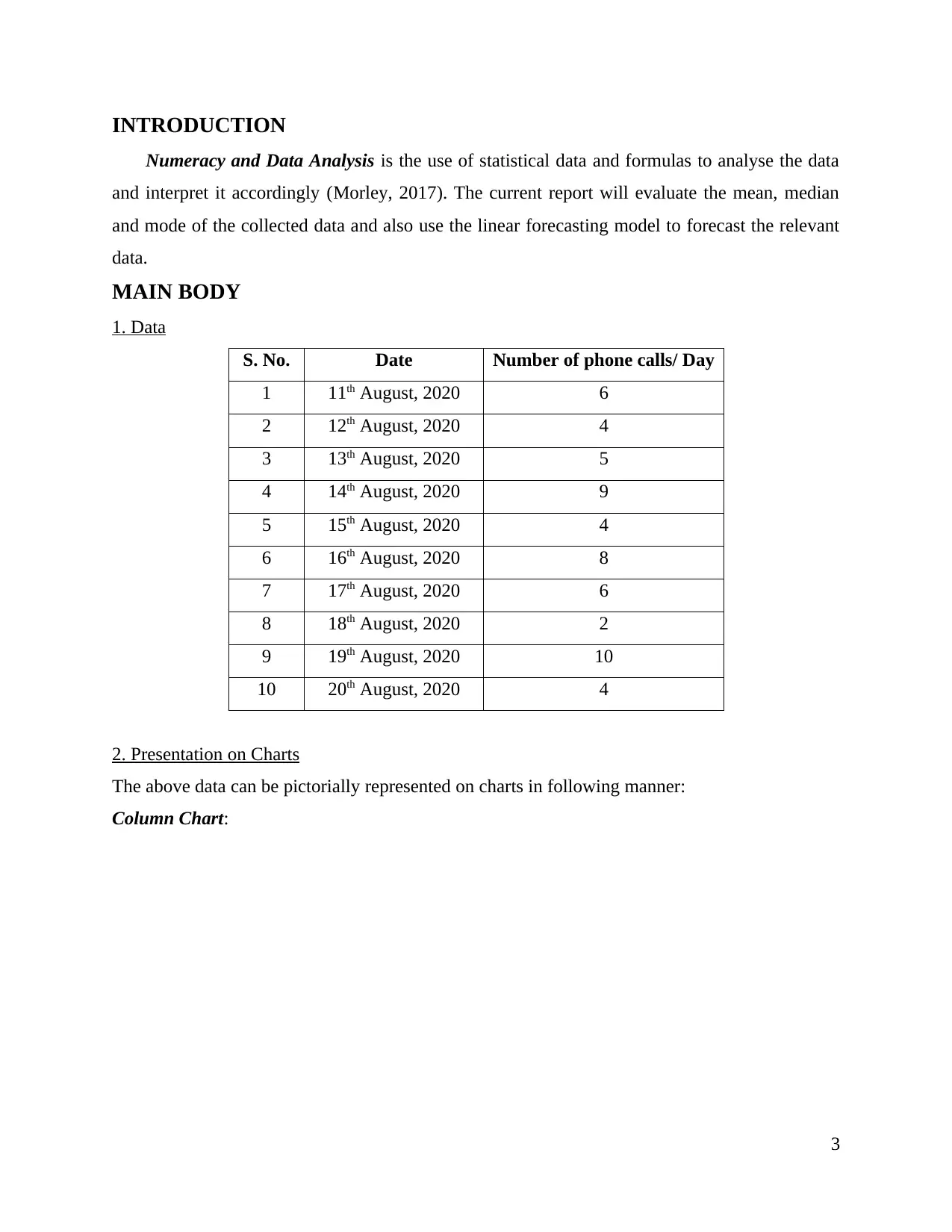
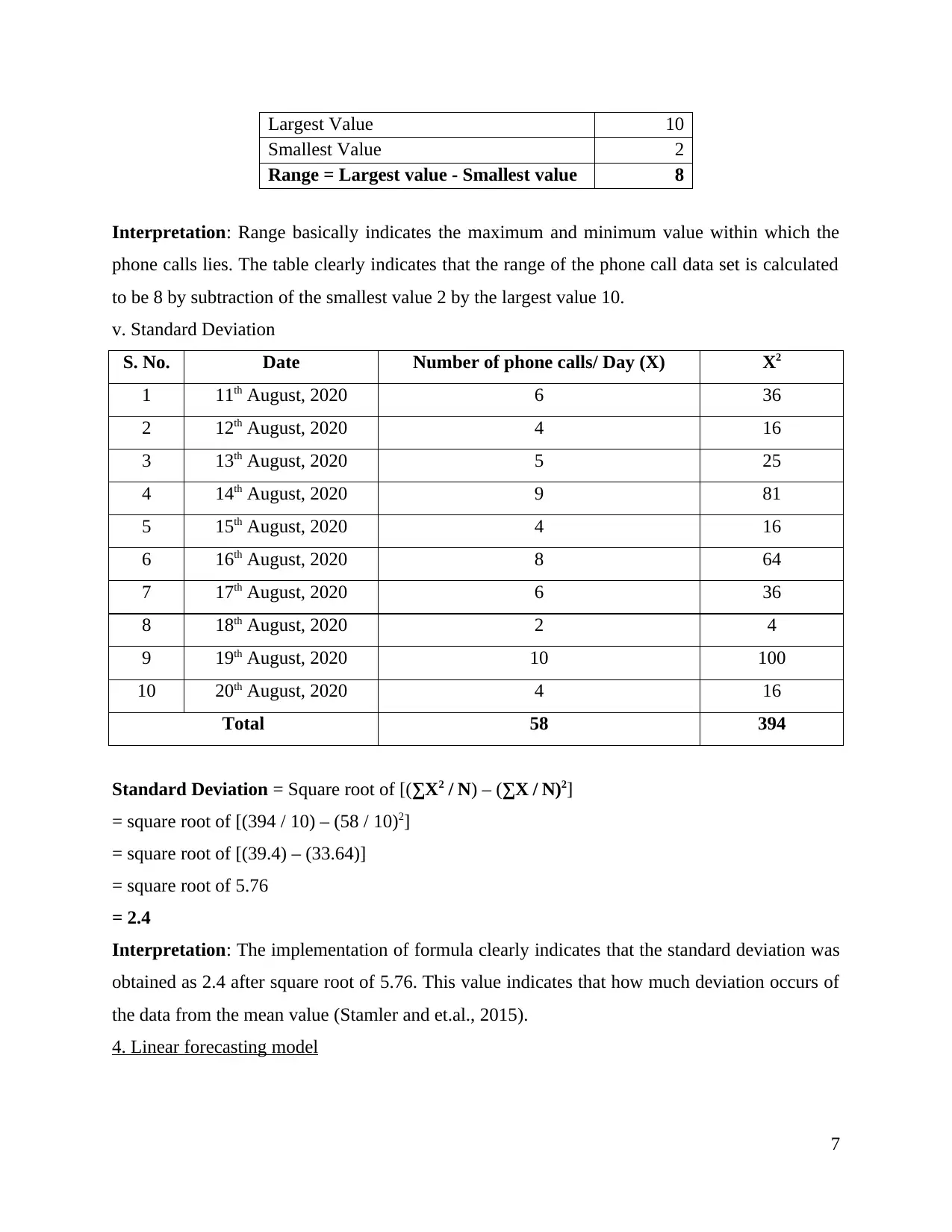
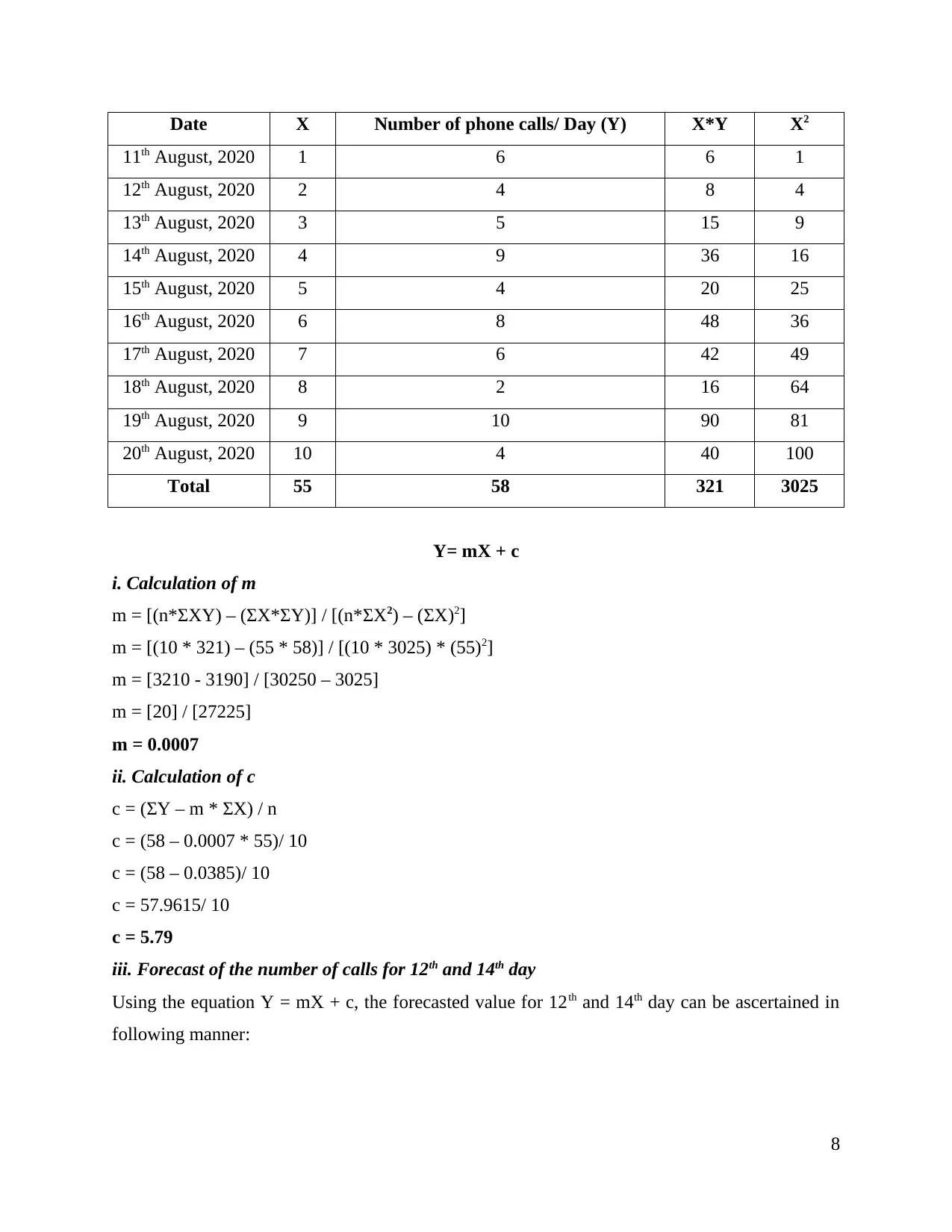
This report presents a comprehensive analysis of a dataset of phone calls over a 10-day period, employing various statistical methods to interpret the data. The report begins with an introduction to numeracy and data analysis, followed by the presentation of the raw data. The main body of the report includes the calculation of descriptive statistics such as mean, median, mode, range, and standard deviation. The mean value of phone calls is calculated to be 5.8, representing the average daily calls. The median, 5.5, indicates the central value of the dataset, while the mode of 4 reflects the most frequent number of calls per day. The range and standard deviation are also computed to provide further insights into the data distribution. Furthermore, a linear forecasting model is developed to predict the number of calls for future days. The report concludes by summarizing the findings and emphasizing the importance of these statistical techniques in data interpretation and prediction. The report references relevant books and journals to support the analysis.
1 out of 11














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)