Indonesian Journal of Electrical Engineering and Computer Science Research 2022
VerifiedAdded on 2022/08/24
|7
|3697
|27
AI Summary
Project: Singapore fifth Newater plant Purpose: To enable participants to apply the tools and techniques of decision analysis to a real world problem and, in the process, to deepen their understanding of decision analysis. Assignment question: Identify a public or private sector decision that was reported in the media in the past five years. The problem should be sufficiently “difficult” to merit decision analysis. Taking a standpoint from before the decision was made; your role is to act as consultants to the decision maker(s) by applying the tools of decision analysis to the problem. Your report should include: • Problem statement and objectives >> ~300 - 400 words • Decision tree structure with expected value analysis >> Provide decision tree • Risk profiles >> 350-400 words • Exploration of key uncertainties >>
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Indonesian Journal of Electrical Engineering and Computer Science
Vol. 5, No. 3, March 2017, pp. 666 ~ 672
DOI: 10.11591/ijeecs.v5.i3.pp666-672 666
Received December 5, 2016; Revised February 10, 2017; Accepted February 25, 2017
Estimation of Turbidity in Water Treatment Plant using
Hammerstein-Wiener and Neural Network Technique
M.S. Gaya*1, M.U. Zango2, L.A. Yusuf 3, Mamunu Mustapha4, Bashir Muhammad5,
Ashiru Sani6, Aminu Tijjani7, N.A. Wahab8, M.T.M. Khairi9
1,4,7Department Electrical Engineering, Kano University of Science & Technology, Wudil
2,6Department of Civil Engineering, Kano University of Science & Technology, Wudil
3Department of Electrical Engineering, Bayero University Kano
8,9Department of Control & Mechatronics, Universiti Teknologi Malaysia, Skudai
*Corresponding author, e-mail: muhdgayasani@gmail.com
Abstract
Turbidity is a measure of water quality. Excessive turbidity poses a threat to health and causes
pollution. Most of the available mathematical models of water treatment plants do not capture turbidity. A
reliable model is essential for effective removal of turbidity in the water treatment plant. This paper
presents a comparison of Hammerstein Wiener and neural network technique for estimating of turbidity in
water treatment plant. The models were validated using an experimental data from Tamburawa water
treatment plant in Kano, Nigeria. Simulation results demonstrated that the neural network model
outperformed the Hammerstein-Wiener model in estimating the turbidity. The neural network model may
serve as a valuable tool for predicting the turbidity in the plant.
Keywords: model, structure, function, neurons, learning
Copyright © 2017 Institute of Advanced Engineering and Science. All rights reserved.
1. Introduction
Turbidity mostly provides cover and food for pathogens. If not effectively removed,
turbidity can cause the outburst of waterborne diseases. An appropriate turbidity model is
absolutely crucial not only for the purpose of control, design, estimation, but also for optimal and
trouble-free operation of the water treatment plant. Water treatment plants are nonlinear in
nature; linear models may not necessarily describe well behaviour of the plant. Nonlinear
mechanistic model may be of advantage since the model is realized from a fundamental
knowledge of the biological, physical, or chemical elements of the plant. Arguably, nonlinear
mechanistic models (ASM model families) [1] are architecturally complex to use, difficult to solve
analytically [2, 3] and do not captured some essential parameters such as turbidity which is
crucial in revealing whether the water is safe for use or not. A reliable empirical model for
prediction of turbidity in water treatment plant is significantly important.
Surveying the literature reveals that several empirical models were developed for
estimating turbidity in the treatment plant either through simulations or practically [4-7].
However, most of these models do not focus on forecasting turbidity in the water treatment
plant. Therefore, it is the objective of this paper to investigate the feasibility and effectiveness of
estimating turbidity in the water treatment plant. Hammerstein Wiener model is quite attractive
due to its convenient block representation and easy implementation. Hammerstein Wiener
model has an effective approximating capability for nonlinear system with large historic data.
Neural network techniques were used in several real-world applications and have proven to be
efficient in handling uncertainty, nonlinearity and complex noisy data. The success of neural
network is as the result of fast learning ability and adaptation.
The performances of the models were evaluated in terms of root mean square error
(RMSE), mean absolute deviation (MAD) and mean absolute percentage error (MAPE). These
measures are the most widely used criteria for evaluating the performance of an estimation
(prediction) model. The paper is organized as follows: section 2 describes the Tamburwa water
treatment plant, neural network and Hammerstein Wiener methods. Section presents the results
and analysis while section 5 dealt with the conclusion.
Vol. 5, No. 3, March 2017, pp. 666 ~ 672
DOI: 10.11591/ijeecs.v5.i3.pp666-672 666
Received December 5, 2016; Revised February 10, 2017; Accepted February 25, 2017
Estimation of Turbidity in Water Treatment Plant using
Hammerstein-Wiener and Neural Network Technique
M.S. Gaya*1, M.U. Zango2, L.A. Yusuf 3, Mamunu Mustapha4, Bashir Muhammad5,
Ashiru Sani6, Aminu Tijjani7, N.A. Wahab8, M.T.M. Khairi9
1,4,7Department Electrical Engineering, Kano University of Science & Technology, Wudil
2,6Department of Civil Engineering, Kano University of Science & Technology, Wudil
3Department of Electrical Engineering, Bayero University Kano
8,9Department of Control & Mechatronics, Universiti Teknologi Malaysia, Skudai
*Corresponding author, e-mail: muhdgayasani@gmail.com
Abstract
Turbidity is a measure of water quality. Excessive turbidity poses a threat to health and causes
pollution. Most of the available mathematical models of water treatment plants do not capture turbidity. A
reliable model is essential for effective removal of turbidity in the water treatment plant. This paper
presents a comparison of Hammerstein Wiener and neural network technique for estimating of turbidity in
water treatment plant. The models were validated using an experimental data from Tamburawa water
treatment plant in Kano, Nigeria. Simulation results demonstrated that the neural network model
outperformed the Hammerstein-Wiener model in estimating the turbidity. The neural network model may
serve as a valuable tool for predicting the turbidity in the plant.
Keywords: model, structure, function, neurons, learning
Copyright © 2017 Institute of Advanced Engineering and Science. All rights reserved.
1. Introduction
Turbidity mostly provides cover and food for pathogens. If not effectively removed,
turbidity can cause the outburst of waterborne diseases. An appropriate turbidity model is
absolutely crucial not only for the purpose of control, design, estimation, but also for optimal and
trouble-free operation of the water treatment plant. Water treatment plants are nonlinear in
nature; linear models may not necessarily describe well behaviour of the plant. Nonlinear
mechanistic model may be of advantage since the model is realized from a fundamental
knowledge of the biological, physical, or chemical elements of the plant. Arguably, nonlinear
mechanistic models (ASM model families) [1] are architecturally complex to use, difficult to solve
analytically [2, 3] and do not captured some essential parameters such as turbidity which is
crucial in revealing whether the water is safe for use or not. A reliable empirical model for
prediction of turbidity in water treatment plant is significantly important.
Surveying the literature reveals that several empirical models were developed for
estimating turbidity in the treatment plant either through simulations or practically [4-7].
However, most of these models do not focus on forecasting turbidity in the water treatment
plant. Therefore, it is the objective of this paper to investigate the feasibility and effectiveness of
estimating turbidity in the water treatment plant. Hammerstein Wiener model is quite attractive
due to its convenient block representation and easy implementation. Hammerstein Wiener
model has an effective approximating capability for nonlinear system with large historic data.
Neural network techniques were used in several real-world applications and have proven to be
efficient in handling uncertainty, nonlinearity and complex noisy data. The success of neural
network is as the result of fast learning ability and adaptation.
The performances of the models were evaluated in terms of root mean square error
(RMSE), mean absolute deviation (MAD) and mean absolute percentage error (MAPE). These
measures are the most widely used criteria for evaluating the performance of an estimation
(prediction) model. The paper is organized as follows: section 2 describes the Tamburwa water
treatment plant, neural network and Hammerstein Wiener methods. Section presents the results
and analysis while section 5 dealt with the conclusion.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

IJEECS ISSN: 2502-4752
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
667
2. Research Method
2.1. Tamburawa Water Treatment Plant
The Tamburawa water treatment plant with a capacity of producing 150Ml portable
water per day to covers communities in Kano city and the surroundings. Kano River is treated in
the plant exceeding the minimum standard water quality limits of world health organization using
conventional treatment processes.
The plant uses contact stabilization activated sludge process for suspended solids,
turbidity and other pollutants removal. The raw (influent) wastewater from the pump station
Figure 1 located on the south bank [8] of Kano river enters the preliminary treatment unit where
the grits contained in wastewater are removed to avoid pump wear and pipe deterioration. Then,
the wastewater goes to the primary clarifier shown Figure 2 in which the wastewater is retained
to allow the settle-able organics and floatable solids to settle at the bottom of the clarifier by
gravity sedimentation.
Figure 1. Effects of selecting different switching
under dynamic condition
Figure 2. Effects of selecting different
switching under dynamic condition
2.2. Neural Network
Neural network has gained vast popularity over the last few decades, particularly in the
field of system identification, modelling and control applications. Neural network is a group of
interconnected neurons based on a mathematical model for processing and transmitting
information. The neurons (nodes) receive an input signal, then process and produce an output.
The connections between the neurons determine the flow of information, which can be in only
one direction or bidirectional. Illustration in Figure 3 demonstrates a neuron architecture.
Figure 3. Neuron structure
Each of the input signal ix is associated with a weight iw which strengthen or deplete
the input signal [9].The model of neuron was proposed [10] and expressed as:
1
n
i i
i
y f w x
(1)
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
667
2. Research Method
2.1. Tamburawa Water Treatment Plant
The Tamburawa water treatment plant with a capacity of producing 150Ml portable
water per day to covers communities in Kano city and the surroundings. Kano River is treated in
the plant exceeding the minimum standard water quality limits of world health organization using
conventional treatment processes.
The plant uses contact stabilization activated sludge process for suspended solids,
turbidity and other pollutants removal. The raw (influent) wastewater from the pump station
Figure 1 located on the south bank [8] of Kano river enters the preliminary treatment unit where
the grits contained in wastewater are removed to avoid pump wear and pipe deterioration. Then,
the wastewater goes to the primary clarifier shown Figure 2 in which the wastewater is retained
to allow the settle-able organics and floatable solids to settle at the bottom of the clarifier by
gravity sedimentation.
Figure 1. Effects of selecting different switching
under dynamic condition
Figure 2. Effects of selecting different
switching under dynamic condition
2.2. Neural Network
Neural network has gained vast popularity over the last few decades, particularly in the
field of system identification, modelling and control applications. Neural network is a group of
interconnected neurons based on a mathematical model for processing and transmitting
information. The neurons (nodes) receive an input signal, then process and produce an output.
The connections between the neurons determine the flow of information, which can be in only
one direction or bidirectional. Illustration in Figure 3 demonstrates a neuron architecture.
Figure 3. Neuron structure
Each of the input signal ix is associated with a weight iw which strengthen or deplete
the input signal [9].The model of neuron was proposed [10] and expressed as:
1
n
i i
i
y f w x
(1)

ISSN: 2502-4752
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
668
Where f is the activation (transfer) function, ix is the input signals, iw depicts the weights and
is the bias. The desired output can be obtained by updating the weights. The process of
updating the weights of a neuron is referred as learning or training. Learning rules are used to
govern the neuron weights updating process and the procedure of utilizing the learning rules to
update the weights is known as learning algorithm.
Based on the learning procedure, neural networks are categorized as supervised or
unsupervised or hybrid. In supervised learning, the neural network is provided with inputs and
the desired outputs. The main concern is to obtain a set of weights that drastically reduces the
error between the network output and desired output. Unsupervised learning uses only input,
the network updates its weights so that similar input yields corresponding output. Hybrid
learning combines supervised and unsupervised learning.
On the other hand, neural networks are classified based on topology (the way the
neurons are ordered and organized from the input layer to the output layer). The two main
topologies are the feed-forward and recurrent neural network. Feed-forward neural network
allows information (data) to flow in only one direction. The network does not possess feedback
(loop), that is connections originating from output of a node to an input of a node in the same
layer or previous layer. This kind of neural network is straightforward and stable. Recurrent
neural networks have feedback in them, and the flow of information is bi-directional. The
presence of the feedback improves their learning abilities and performances. Recurrent
networks are referred as dynamic neural networks.
Once an appropriate topology is defined for a particular application, the choices of
suitable network parameters are essential for effective learning and better performance. Some
of these parameters include the number of hidden layers, number of hidden neurons, transfer
functions, number of training epochs and learning rate.
Number of Hidden Layers: The generalization capability of a neural network is linked
to its hidden layer. Too many hidden layers in a network increases computational burden and
causes over-fitting which results in poor prediction. Several studies shows that one or two
hidden layers mostly produce better performance. As indicated in [11] that problems that require
two hidden layers are only rarely encountered in real-life situations. One hidden layer suffices
for most of the real-world problems. In this study, each of the neural network inverse model
uses one hidden layer.
Number of Neurons in the Hidden Layer: Deciding the appropriate number of
neurons to use is crucial for effective learning and performance of the network. Nevertheless,
there is no systematic approach to determine the optimal number of neurons to utilize for a
problem. Some rule-of-thumb methods have been foremost to choose the number of neurons in
the hidden layer. A geometric pyramid rule was proposed which state that for a three-layer
neural network having n input neurons and m output neurons, then the hidden layer would
have n m neurons [11]. It was indicated that the number of neurons should be between the
size of the input neurons and the size of output neurons [12]. Also [13] demonstrates that the
optimal number of neurons would mostly be obtained between one-half (1/2) to three (3) times
the number of input neurons. Based on these proposals and trial error method, ten (10) hidden
neurons were chosen.
Transfer Function: Most of the real-world processes are nonlinear in nature indicating
that linear transfer functions may not be useful for modelling and control of such processes.
Transfer functions such as sigmoid transfer function are widely used because they are smooth,
nonlinear, continuous and monotonically increasing. The derivative of the sigmoid function has
an attractive feature which makes its evaluation easier.
Learning Rate: Learning rate controls the size of weight and bias changes during
training. If the learning rate is too large, the network fails to converge with allowable error over
training set. For a too low learning rate, the training takes much longer thereby resulting in slow
performance. Most of the neural networks utilized a usual value (0.3) of the learning rate.
Momentum: Momentum parameter impedes the network from converging to a local
minima. Too high value of momentum causes the network to oscillate (becoming unstable) and
too low value results in local minima trapping and slow down the network training. Typical value
(0.05) is widely used.
Training Epochs: Many epochs are needed to train a neural network. For a network
training by error, epoch represents the maximum number of iterations. As suggested [11] to
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
668
Where f is the activation (transfer) function, ix is the input signals, iw depicts the weights and
is the bias. The desired output can be obtained by updating the weights. The process of
updating the weights of a neuron is referred as learning or training. Learning rules are used to
govern the neuron weights updating process and the procedure of utilizing the learning rules to
update the weights is known as learning algorithm.
Based on the learning procedure, neural networks are categorized as supervised or
unsupervised or hybrid. In supervised learning, the neural network is provided with inputs and
the desired outputs. The main concern is to obtain a set of weights that drastically reduces the
error between the network output and desired output. Unsupervised learning uses only input,
the network updates its weights so that similar input yields corresponding output. Hybrid
learning combines supervised and unsupervised learning.
On the other hand, neural networks are classified based on topology (the way the
neurons are ordered and organized from the input layer to the output layer). The two main
topologies are the feed-forward and recurrent neural network. Feed-forward neural network
allows information (data) to flow in only one direction. The network does not possess feedback
(loop), that is connections originating from output of a node to an input of a node in the same
layer or previous layer. This kind of neural network is straightforward and stable. Recurrent
neural networks have feedback in them, and the flow of information is bi-directional. The
presence of the feedback improves their learning abilities and performances. Recurrent
networks are referred as dynamic neural networks.
Once an appropriate topology is defined for a particular application, the choices of
suitable network parameters are essential for effective learning and better performance. Some
of these parameters include the number of hidden layers, number of hidden neurons, transfer
functions, number of training epochs and learning rate.
Number of Hidden Layers: The generalization capability of a neural network is linked
to its hidden layer. Too many hidden layers in a network increases computational burden and
causes over-fitting which results in poor prediction. Several studies shows that one or two
hidden layers mostly produce better performance. As indicated in [11] that problems that require
two hidden layers are only rarely encountered in real-life situations. One hidden layer suffices
for most of the real-world problems. In this study, each of the neural network inverse model
uses one hidden layer.
Number of Neurons in the Hidden Layer: Deciding the appropriate number of
neurons to use is crucial for effective learning and performance of the network. Nevertheless,
there is no systematic approach to determine the optimal number of neurons to utilize for a
problem. Some rule-of-thumb methods have been foremost to choose the number of neurons in
the hidden layer. A geometric pyramid rule was proposed which state that for a three-layer
neural network having n input neurons and m output neurons, then the hidden layer would
have n m neurons [11]. It was indicated that the number of neurons should be between the
size of the input neurons and the size of output neurons [12]. Also [13] demonstrates that the
optimal number of neurons would mostly be obtained between one-half (1/2) to three (3) times
the number of input neurons. Based on these proposals and trial error method, ten (10) hidden
neurons were chosen.
Transfer Function: Most of the real-world processes are nonlinear in nature indicating
that linear transfer functions may not be useful for modelling and control of such processes.
Transfer functions such as sigmoid transfer function are widely used because they are smooth,
nonlinear, continuous and monotonically increasing. The derivative of the sigmoid function has
an attractive feature which makes its evaluation easier.
Learning Rate: Learning rate controls the size of weight and bias changes during
training. If the learning rate is too large, the network fails to converge with allowable error over
training set. For a too low learning rate, the training takes much longer thereby resulting in slow
performance. Most of the neural networks utilized a usual value (0.3) of the learning rate.
Momentum: Momentum parameter impedes the network from converging to a local
minima. Too high value of momentum causes the network to oscillate (becoming unstable) and
too low value results in local minima trapping and slow down the network training. Typical value
(0.05) is widely used.
Training Epochs: Many epochs are needed to train a neural network. For a network
training by error, epoch represents the maximum number of iterations. As suggested [11] to

IJEECS ISSN: 2502-4752
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
669
train until you can’t stand it anymore. Several studies indicated that convergence could be
achieved with training epochs from 85 to 5000 epochs.
2.2.1. Neural Network Modelling
The raw data was collected from the Tamburawa Water Treatment Plant. The data
contained missing values, erroneous values, outliers and corrupted measurements. These were
treated using of priori knowledge and mean value, since the quality of the data is essential
in achieving an accurate and reliable prediction. Larger portions of the data sets (90%) were
used for model training and small portion (10%) for testing, since training data set is kept for
realizing the model. The testing data set is meant to ascertain the generalization capability of
the developed model.
This paper uses feedforward neural network to develop the model. The neural network
has three layers with an input layer containing the input variables connected to hidden layer
having ten (10) neurons followed by the output layer. The tan-sigmoid (TANSIG) and purelin
(PURELIN) were utilized as the transfer functions for the hidden layer and the output layer
respectively. The back-propagation method is used to train the neural network for 1000 training
epochs. After the training stage stopped, the realized neural network model was provided with
the testing data. The prediction ability is measured based on the performance criteria using
RMSE, MAD and MAPE.
2.3. Hammerstein- Weiner Model
The ability of the Hammerstein-Wiener model to be used as a black-box model in some
applications since it provides flexible parameterization and as a grey-box model because it
captures fundamental knowledge regarding process characteristics made it quite attractive in
estimation problem. A model in which a nonlinear block both precedes and follows a linear
dynamic system is referred as Hammerstein- Wiener model [14]. The Figure 4 shows the
structure of Hammerstein-Wiener model.
u(t) Input
nonlinearity
f
Linear
block
B/F
Output
nonlinearity
h
w(t) x(t) y(t)
Figure 4. Schematic of Hammerstein-Wiener model
w t f u t is a nonlinear function converting input data.
Bx t w t F depicts linear function, f and h act on the input and output port of the linear
block respectively. The function w t and x t are variables that define the input and output of
the linear block. This structure represent a straightforward technique to develop nonlinear
estimator [15].
2.3.1. Hammerstein-Wiener Modelling
The same data used for developing neural network model was utilized in realizing the
Hammerstein-Weiner model.The Hammerstein-Wiener model is built using MATLAB system
identification toolbox based on the configuration where the input and output nonlinearity
estimators are both piecewise linear functions with number of unit equals to 10. The model has
order of 2bn , 3fn and 1kn .
3. Results and Analysis
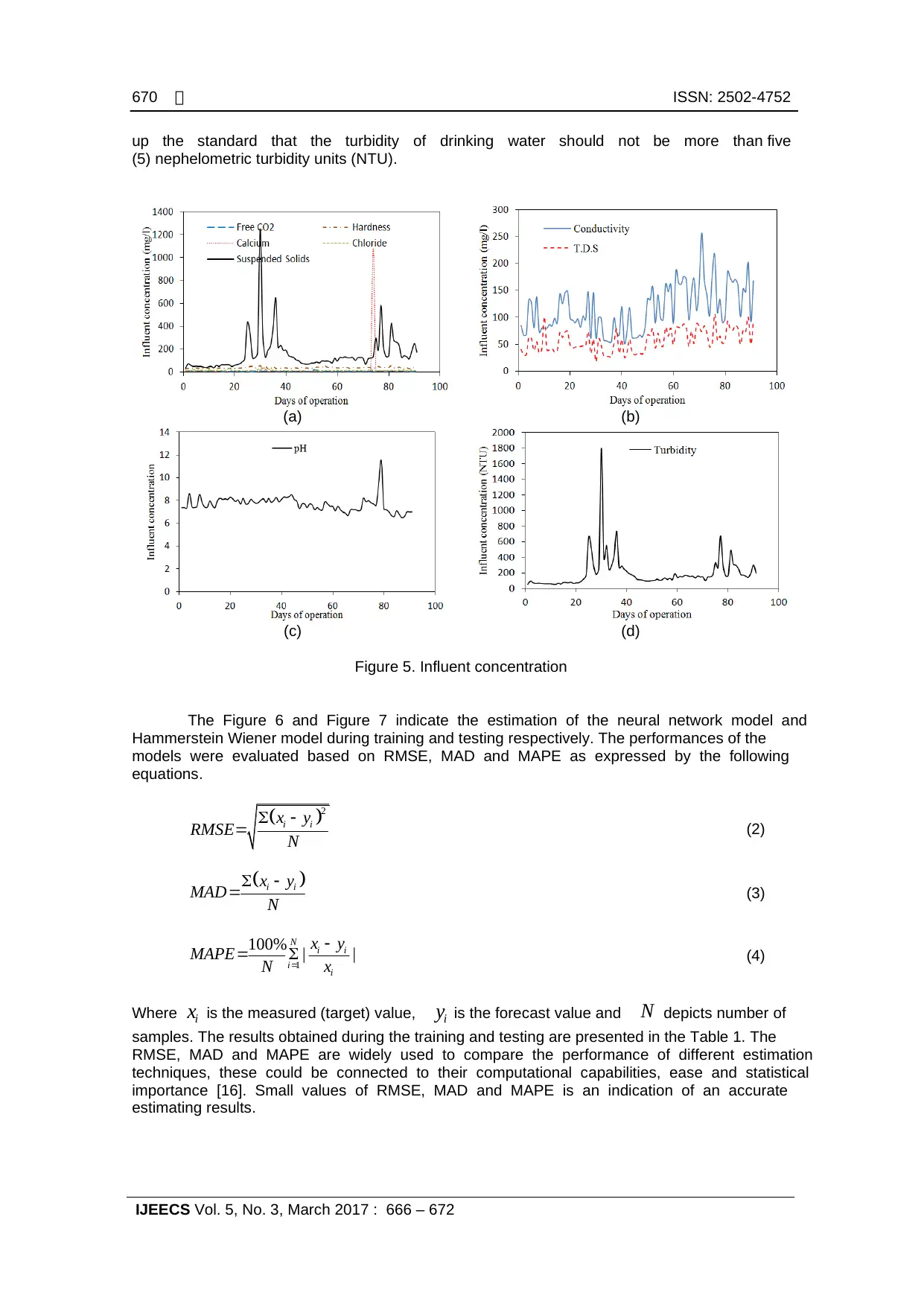
The illustrations in Figure 5(a-d) show some of the Tamburawa Water Treatment Plant
influents. For environmental and public health concern, the concentration of the effluent must be
within the allowable limits defined by the regulatory bodies. The World Health Organization sets
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
669
train until you can’t stand it anymore. Several studies indicated that convergence could be
achieved with training epochs from 85 to 5000 epochs.
2.2.1. Neural Network Modelling
The raw data was collected from the Tamburawa Water Treatment Plant. The data
contained missing values, erroneous values, outliers and corrupted measurements. These were
treated using of priori knowledge and mean value, since the quality of the data is essential
in achieving an accurate and reliable prediction. Larger portions of the data sets (90%) were
used for model training and small portion (10%) for testing, since training data set is kept for
realizing the model. The testing data set is meant to ascertain the generalization capability of
the developed model.
This paper uses feedforward neural network to develop the model. The neural network
has three layers with an input layer containing the input variables connected to hidden layer
having ten (10) neurons followed by the output layer. The tan-sigmoid (TANSIG) and purelin
(PURELIN) were utilized as the transfer functions for the hidden layer and the output layer
respectively. The back-propagation method is used to train the neural network for 1000 training
epochs. After the training stage stopped, the realized neural network model was provided with
the testing data. The prediction ability is measured based on the performance criteria using
RMSE, MAD and MAPE.
2.3. Hammerstein- Weiner Model
The ability of the Hammerstein-Wiener model to be used as a black-box model in some
applications since it provides flexible parameterization and as a grey-box model because it
captures fundamental knowledge regarding process characteristics made it quite attractive in
estimation problem. A model in which a nonlinear block both precedes and follows a linear
dynamic system is referred as Hammerstein- Wiener model [14]. The Figure 4 shows the
structure of Hammerstein-Wiener model.
u(t) Input
nonlinearity
f
Linear
block
B/F
Output
nonlinearity
h
w(t) x(t) y(t)
Figure 4. Schematic of Hammerstein-Wiener model
w t f u t is a nonlinear function converting input data.
Bx t w t F depicts linear function, f and h act on the input and output port of the linear
block respectively. The function w t and x t are variables that define the input and output of
the linear block. This structure represent a straightforward technique to develop nonlinear
estimator [15].
2.3.1. Hammerstein-Wiener Modelling
The same data used for developing neural network model was utilized in realizing the
Hammerstein-Weiner model.The Hammerstein-Wiener model is built using MATLAB system
identification toolbox based on the configuration where the input and output nonlinearity
estimators are both piecewise linear functions with number of unit equals to 10. The model has
order of 2bn , 3fn and 1kn .
3. Results and Analysis
The illustrations in Figure 5(a-d) show some of the Tamburawa Water Treatment Plant
influents. For environmental and public health concern, the concentration of the effluent must be
within the allowable limits defined by the regulatory bodies. The World Health Organization sets
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
ISSN: 2502-4752
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
670
up the standard that the turbidity of drinking water should not be more than five
(5) nephelometric turbidity units (NTU).
(a) (b)
(c) (d)
Figure 5. Influent concentration
The Figure 6 and Figure 7 indicate the estimation of the neural network model and
Hammerstein Wiener model during training and testing respectively. The performances of the
models were evaluated based on RMSE, MAD and MAPE as expressed by the following
equations.
2
i ix y
RMSE N
(2)
i ix y
MAD N
(3)
1
100% | |
N i i
i i
x y
MAPE N x
(4)
Where ix is the measured (target) value, iy is the forecast value and N depicts number of
samples. The results obtained during the training and testing are presented in the Table 1. The
RMSE, MAD and MAPE are widely used to compare the performance of different estimation
techniques, these could be connected to their computational capabilities, ease and statistical
importance [16]. Small values of RMSE, MAD and MAPE is an indication of an accurate
estimating results.
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
670
up the standard that the turbidity of drinking water should not be more than five
(5) nephelometric turbidity units (NTU).
(a) (b)
(c) (d)
Figure 5. Influent concentration
The Figure 6 and Figure 7 indicate the estimation of the neural network model and
Hammerstein Wiener model during training and testing respectively. The performances of the
models were evaluated based on RMSE, MAD and MAPE as expressed by the following
equations.
2
i ix y
RMSE N
(2)
i ix y
MAD N
(3)
1
100% | |
N i i
i i
x y
MAPE N x
(4)
Where ix is the measured (target) value, iy is the forecast value and N depicts number of
samples. The results obtained during the training and testing are presented in the Table 1. The
RMSE, MAD and MAPE are widely used to compare the performance of different estimation
techniques, these could be connected to their computational capabilities, ease and statistical
importance [16]. Small values of RMSE, MAD and MAPE is an indication of an accurate
estimating results.
IJEECS ISSN: 2502-4752
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
671
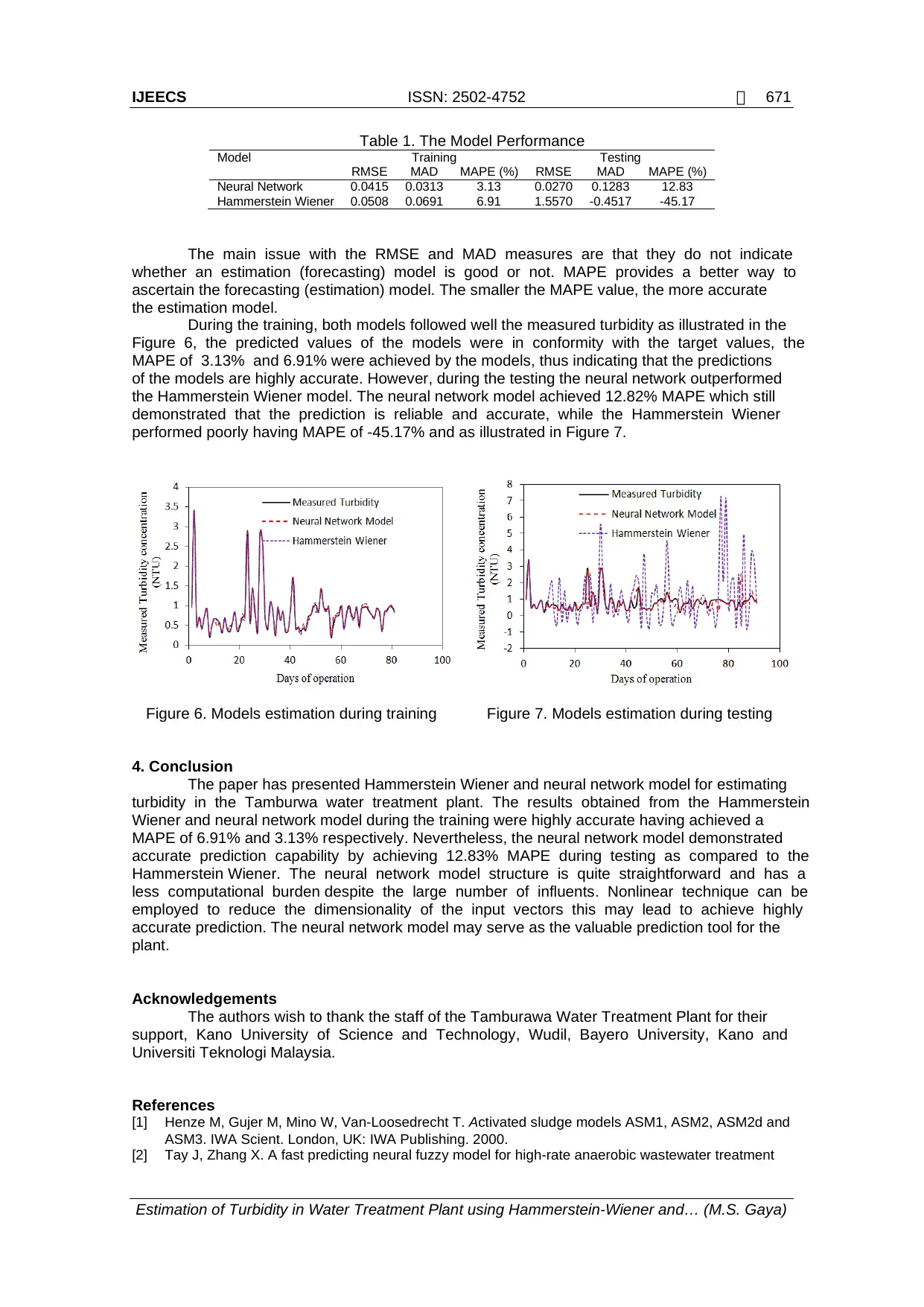
Table 1. The Model Performance
Model Training Testing
RMSE MAD MAPE (%) RMSE MAD MAPE (%)
Neural Network 0.0415 0.0313 3.13 0.0270 0.1283 12.83
Hammerstein Wiener 0.0508 0.0691 6.91 1.5570 -0.4517 -45.17
The main issue with the RMSE and MAD measures are that they do not indicate
whether an estimation (forecasting) model is good or not. MAPE provides a better way to
ascertain the forecasting (estimation) model. The smaller the MAPE value, the more accurate
the estimation model.
During the training, both models followed well the measured turbidity as illustrated in the
Figure 6, the predicted values of the models were in conformity with the target values, the
MAPE of 3.13% and 6.91% were achieved by the models, thus indicating that the predictions
of the models are highly accurate. However, during the testing the neural network outperformed
the Hammerstein Wiener model. The neural network model achieved 12.82% MAPE which still
demonstrated that the prediction is reliable and accurate, while the Hammerstein Wiener
performed poorly having MAPE of -45.17% and as illustrated in Figure 7.
Figure 6. Models estimation during training Figure 7. Models estimation during testing
4. Conclusion
The paper has presented Hammerstein Wiener and neural network model for estimating
turbidity in the Tamburwa water treatment plant. The results obtained from the Hammerstein
Wiener and neural network model during the training were highly accurate having achieved a
MAPE of 6.91% and 3.13% respectively. Nevertheless, the neural network model demonstrated
accurate prediction capability by achieving 12.83% MAPE during testing as compared to the
Hammerstein Wiener. The neural network model structure is quite straightforward and has a
less computational burden despite the large number of influents. Nonlinear technique can be
employed to reduce the dimensionality of the input vectors this may lead to achieve highly
accurate prediction. The neural network model may serve as the valuable prediction tool for the
plant.
Acknowledgements
The authors wish to thank the staff of the Tamburawa Water Treatment Plant for their
support, Kano University of Science and Technology, Wudil, Bayero University, Kano and
Universiti Teknologi Malaysia.
References
[1] Henze M, Gujer M, Mino W, Van-Loosedrecht T. Activated sludge models ASM1, ASM2, ASM2d and
ASM3. IWA Scient. London, UK: IWA Publishing. 2000.
[2] Tay J, Zhang X. A fast predicting neural fuzzy model for high-rate anaerobic wastewater treatment
Estimation of Turbidity in Water Treatment Plant using Hammerstein-Wiener and… (M.S. Gaya)
671
Table 1. The Model Performance
Model Training Testing
RMSE MAD MAPE (%) RMSE MAD MAPE (%)
Neural Network 0.0415 0.0313 3.13 0.0270 0.1283 12.83
Hammerstein Wiener 0.0508 0.0691 6.91 1.5570 -0.4517 -45.17
The main issue with the RMSE and MAD measures are that they do not indicate
whether an estimation (forecasting) model is good or not. MAPE provides a better way to
ascertain the forecasting (estimation) model. The smaller the MAPE value, the more accurate
the estimation model.
During the training, both models followed well the measured turbidity as illustrated in the
Figure 6, the predicted values of the models were in conformity with the target values, the
MAPE of 3.13% and 6.91% were achieved by the models, thus indicating that the predictions
of the models are highly accurate. However, during the testing the neural network outperformed
the Hammerstein Wiener model. The neural network model achieved 12.82% MAPE which still
demonstrated that the prediction is reliable and accurate, while the Hammerstein Wiener
performed poorly having MAPE of -45.17% and as illustrated in Figure 7.
Figure 6. Models estimation during training Figure 7. Models estimation during testing
4. Conclusion
The paper has presented Hammerstein Wiener and neural network model for estimating
turbidity in the Tamburwa water treatment plant. The results obtained from the Hammerstein
Wiener and neural network model during the training were highly accurate having achieved a
MAPE of 6.91% and 3.13% respectively. Nevertheless, the neural network model demonstrated
accurate prediction capability by achieving 12.83% MAPE during testing as compared to the
Hammerstein Wiener. The neural network model structure is quite straightforward and has a
less computational burden despite the large number of influents. Nonlinear technique can be
employed to reduce the dimensionality of the input vectors this may lead to achieve highly
accurate prediction. The neural network model may serve as the valuable prediction tool for the
plant.
Acknowledgements
The authors wish to thank the staff of the Tamburawa Water Treatment Plant for their
support, Kano University of Science and Technology, Wudil, Bayero University, Kano and
Universiti Teknologi Malaysia.
References
[1] Henze M, Gujer M, Mino W, Van-Loosedrecht T. Activated sludge models ASM1, ASM2, ASM2d and
ASM3. IWA Scient. London, UK: IWA Publishing. 2000.
[2] Tay J, Zhang X. A fast predicting neural fuzzy model for high-rate anaerobic wastewater treatment

ISSN: 2502-4752
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
672
systems. Water Res. 2000; 34(11): 2849-2860.
[3] Jeppsson U. A simplified control-oriented model of the activated sludge process. Math. Model. Syst.
1995; 1(1): 3-16.
[4] Khairi MTM, Ibrahim S, Yunus MAM, Faramarzi M, Yusuf Z. Artificial Neural Network Approach for
Predicting the Water Turbidity Level. Arab. J. Sci. Eng. 2015; 41(9): 3369-3379.
[5] Iglesias C, Torres JM, Nieto PJG. Turbidity Prediction in a River Basin by Using Artificial Neural
Networks : A Case Study in Northern Spain. Water Resour. Manag. 2014; 28 (2): 319-331.
[6] Rak A. Water Turbidity Modelling During Water Treatment Processes Using Artificial Neural
Networks. Int. J. Water Sci. 2013; 2: 1.
[7] Kabsch-Korbutowicz M, Kutyłowska M. Use of artificial intelligence in predicting the turbidity retention
coefficient during ultrafiltration of water. Environ. Prot. Eng. 2011; 37(2): 75-84.
[8] Tamburawa.pdf. http://www.pciafrica.com. 2015.
[9] Engelbrecht A. Computational intelligence: An introduction. 2nd Edition. John Wiley & Sons Ltd.
2007.
[10] McCulloch W, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull. Math.
Biophys. 1943; 5: 115-133.
[11] Masters T. Practical neural network recipes in C++. New York: Academic Press. 1993.
[12] Heaton J. Introduction to neural networks with Java. Second Edition. USA: Heaton Research Inc.
2008.
[13] Katz J. Developing neural network forecasters for trading. Tech. Anal. Stock. Commod. 1992; 8: 58-
70.
[14] Wills A, Schön TB, Ljung L, Ninness B. Identification of Hammerstein – Wiener models. Automatica.
2013; 49 (1): 70-81.
[15] Safon G, Salazar A. Wiener Systems for Reconstruction of missing Seismic Traces. Proceedings of
International Joint Conference on Neural Networks. San Jose, California, USA. 2011: 1049-1053.
[16] Lawrence KD, Klimberg RK, Lawrence SM. Fundamental of Forecasting using Excel. 2
nd Edition.
New York: Industrial Press Inc. 2008: 57-61.
IJEECS Vol. 5, No. 3, March 2017 : 666 – 672
672
systems. Water Res. 2000; 34(11): 2849-2860.
[3] Jeppsson U. A simplified control-oriented model of the activated sludge process. Math. Model. Syst.
1995; 1(1): 3-16.
[4] Khairi MTM, Ibrahim S, Yunus MAM, Faramarzi M, Yusuf Z. Artificial Neural Network Approach for
Predicting the Water Turbidity Level. Arab. J. Sci. Eng. 2015; 41(9): 3369-3379.
[5] Iglesias C, Torres JM, Nieto PJG. Turbidity Prediction in a River Basin by Using Artificial Neural
Networks : A Case Study in Northern Spain. Water Resour. Manag. 2014; 28 (2): 319-331.
[6] Rak A. Water Turbidity Modelling During Water Treatment Processes Using Artificial Neural
Networks. Int. J. Water Sci. 2013; 2: 1.
[7] Kabsch-Korbutowicz M, Kutyłowska M. Use of artificial intelligence in predicting the turbidity retention
coefficient during ultrafiltration of water. Environ. Prot. Eng. 2011; 37(2): 75-84.
[8] Tamburawa.pdf. http://www.pciafrica.com. 2015.
[9] Engelbrecht A. Computational intelligence: An introduction. 2nd Edition. John Wiley & Sons Ltd.
2007.
[10] McCulloch W, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull. Math.
Biophys. 1943; 5: 115-133.
[11] Masters T. Practical neural network recipes in C++. New York: Academic Press. 1993.
[12] Heaton J. Introduction to neural networks with Java. Second Edition. USA: Heaton Research Inc.
2008.
[13] Katz J. Developing neural network forecasters for trading. Tech. Anal. Stock. Commod. 1992; 8: 58-
70.
[14] Wills A, Schön TB, Ljung L, Ninness B. Identification of Hammerstein – Wiener models. Automatica.
2013; 49 (1): 70-81.
[15] Safon G, Salazar A. Wiener Systems for Reconstruction of missing Seismic Traces. Proceedings of
International Joint Conference on Neural Networks. San Jose, California, USA. 2011: 1049-1053.
[16] Lawrence KD, Klimberg RK, Lawrence SM. Fundamental of Forecasting using Excel. 2
nd Edition.
New York: Industrial Press Inc. 2008: 57-61.
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
