Influence of Age, Smoker, BMI, maxBMI, and minBMI on spBMD

This study investigates the influence of Age, Smoker, BMI, maxBMI, and minBMI on spBMD. Results showed that only Age and BMI had significant influence on spBMD.

Statistics
Name:
Institution:
20th May 2018

Introduction
Osteoporosis has been regarded as a major problem. Osteoporosis refers to a bone disease in
which the bones become weak and are more likely to break. The only way to accurately test the
strength and solidness of the bones is with bone mineral density (BMD) tests. The Rowett
Institute in conjunction with the Aberdeen Royal Infirmary conducted a slimming clinic in 1990.
For 91 post-menopausal women data were collected on the many variables including the six
variables given in the table below.
Variab
le Description
spBMD Bone Mineral Density for the
Lumbar Spine
Age Age in years
Smoke
r 1 = Yes, 0 = No
BMI Current Body Mass Index
maxB
MI Maximum Body Mass Index
minBM
I Minimum Body Mass Index
Body Mass Index (BMI) is a widely used measure assess whether the weight
of an individual is in the healthy range. According to the Australian
Government Department of Health, a BMI between 18.5 and 24.9 for adults
is considered to be within the healthy weight range. A person with a BMI
below 18.5 is considered to be underweight, a person with a BMI above 30 is
considered to be obese and a person with a BMI between 25 and 30 is
considered to be overweight. There are exceptions, for example, the healthy
weight BMI range tends to be higher for older people.

In this study therefore, we sought to investigate whether the variables Age,
Smoker, BMI, maxBMI, and minBMI influence spBMD. We present the results
of the analysis in the next section.
Scatterplots
SPBMD versus Age
The scatter plot below shows that a negative relationship exists between
spBMD and Age (Emerson, Green, Schoerke, & Crowley, 2013). That is to
mean that an increase in the age of the respondent would be expected to
result to a decrease in the spBMD while a decrease in the age of the
respondent would be expected to result in an increase in the spBMD.
SPBMD versus BMI

A scatter plot of spBMD versus BMI was also plotted in order to visualize the
relationship that exists between the two variables. For this case (spBMD
versus BMI), we observe that a positive relationship exists between the two
variables (Friendly & Denis, 2005). That is to mean that an increase in the
BMI of the respondent would be expected to result to an increase in the
spBMD while a decrease in the age of the respondent would be expected to
result in a decrease in the spBMD.
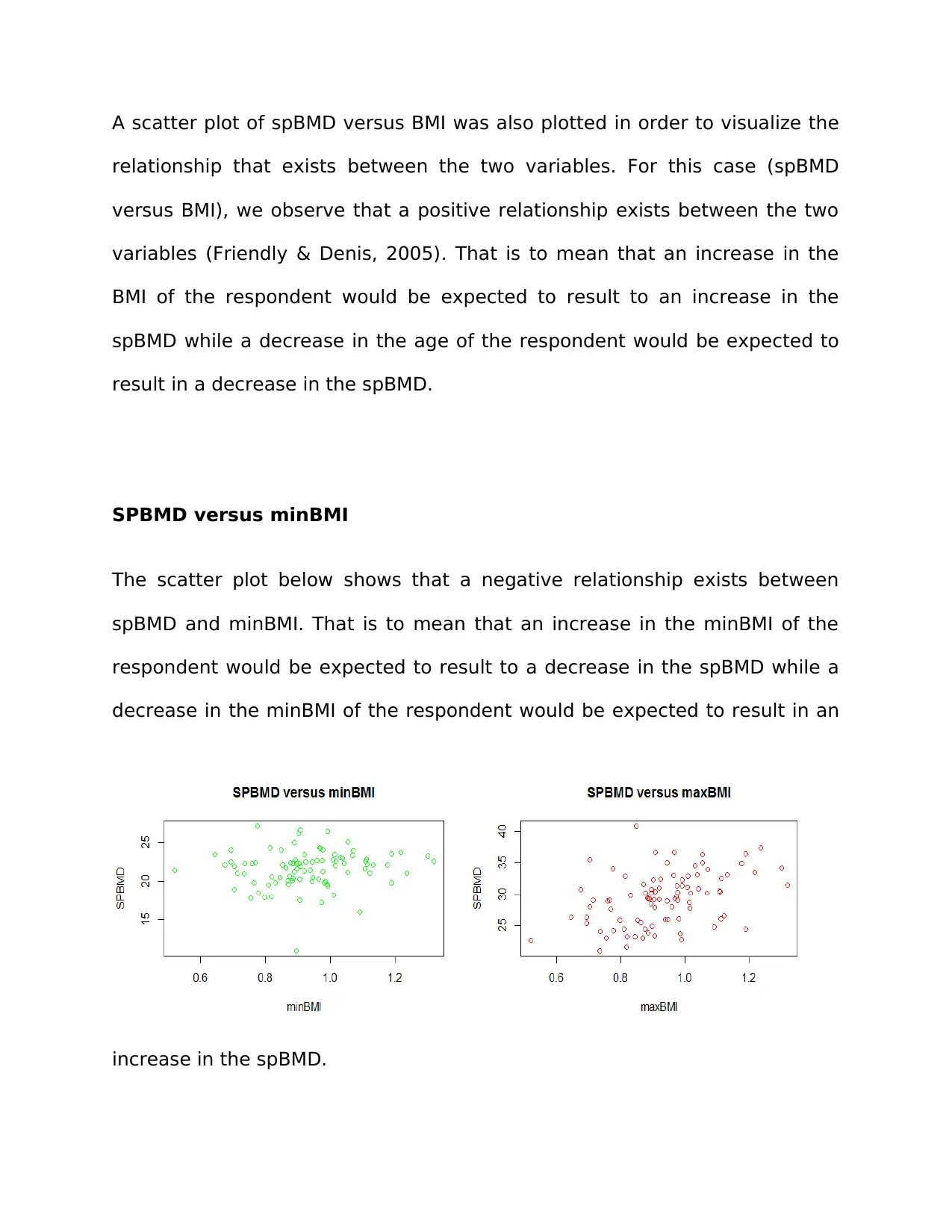
SPBMD versus minBMI
The scatter plot below shows that a negative relationship exists between
spBMD and minBMI. That is to mean that an increase in the minBMI of the
respondent would be expected to result to a decrease in the spBMD while a
decrease in the minBMI of the respondent would be expected to result in an
increase in the spBMD.

SPBMD versus maxBMI
For the spBMD versus maxBMI we observe a positive relationship exists
between spBMD and maxBMI. That is to mean that an increase in the age of
the respondent would be expected to result to an increase in the spBMD
while a decrease in the maxBMI of the respondent would be expected to
result in an increase in the spBMD.
Box Plot
In this section, we present the box plots for the different variables. Considering spBMD, we can
see that the distribution of the data for spBMD seems to be normally distributed. However, it has
some outliers both on the top and bottom of the graph.

The boxplot for the BMI also shows the data to be
normally distributed though it has numerous outliers. The one for minBMI however does not
show normality but a rather skewed distribution with few outliers both at the bottom and at the
top. Lastly, for the maxBMI, the distribution is normally distributed with no evidence of outliers
in the data.
Results
In order to investigate the relationship between spBMD and the five independent variables (Age,
Smoker, BMI, maxBMI, and minBMI), we performed a regression analysis (Armstrong, 2012).
Regression analysis is a mathematical technique that allows one to estimate dependent variable
based on one or more independent variables (Rouaud, 2013). The results are presented in the
table below;
> fit <- lm(spBMD ~ Age
+ Smoker + BMI +
minBMI +maxBMI,
data=data)
> summary(fit)
Call:
lm(formula = spBMD ~
Age + Smoker + BMI +
minBMI + maxBMI, data
= data)
Residuals:

As can be seen, the value of R-squared is 0.2897; this means that only 28.97% of the variation in
the dependent variable (spBMD) is explained by the five independent variables in the model.
The p-value of the F-Statistic is 0.000 (a value less than 5% level of significance), this leads to
rejection of the null hypothesis and concluding that the model is different from zero hence it is fit
and appropriate to estimate the spBMD at 5% level of significance (Tofallis, 2009).
Looking at the individual independent variables, we observed that out of the five independent
variables only 2 were significant in the model. This means that only the two independent
variables are significantly related with the dependent variable. The two significant variables are
Age and BMI. The other three variables (Smoker, minBMI and mxBMI) were found to be
insignificant in the model.
The coefficient of the Age was found to be -0.008137; this suggests that a unit increase in the
age of the participant would result to a decrease in the spBMD by 0.0081. Conversely, a unit
decrease in the age of the participant would result to an increase in the spBMD by 0.0081.
The coefficient of the BMI was found to be 0.014907; this suggests that a unit increase in the
BMI of the respondent would result to an increase in the spBMD by 0.0149. Similarly, a unit
decrease in the BMI of the participant would result to a decrease in the spBMD by 0.0149.
The coefficient of the Smoker was found to be -0.064940; this suggests that being a smoker
would reduce the spBMD by 0.0649.
The coefficient of the minBMI was found to be -0.010276; this suggests that a unit increase in
the minBMI of the participant would result to a decrease in the spBMD by 0.0103. Conversely, a
unit decrease in the minBMI of the respondent would result to an increase in the spBMD by
0.0103.

The coefficient of the maxBMI was found to be 0.004401; this suggests that a unit increase in
the maxBMI of the participant would result to an increase in the spBMD by 0.044. Similarly, a
unit decrease in the maxBMI of the participant would result to a decrease in the spBMD by
0.0044.
Conclusion
The aim of this study was to investigate the influence that variables Age, Smoker, BMI,
maxBMI, and minBMI have on spBMD. Results showed that only Age and BMI
had significant influence on spBMD. Age for instance, had a negative
relationship with spBMD while BMI had a positive relationship with spBMD.

References
Armstrong, J. S. (2012). Illusions in Regression Analysis. International Journal of Forecasting
(forthcoming), 28(3), 689.
Emerson, J. W., Green, W. A., Schoerke, B., & Crowley, J. (2013). The Generalized Pairs Plot.
Journal of Computational and Graphical Statistics, 22(1), 79–91.
Friendly, M., & Denis, D. (2005). The early origins and development of the scatterplot. Journal
of the History of the Behavioral Sciences, 41(2), 103–130.
Rouaud, M. (2013). Probability, Statistics and Estimation. 60.
Tofallis, C. (2009). Least Squares Percentage Regression. Journal of Modern Applied Statistical
Methods, 7(5), 526–534.

Appendix
Rcodes
data <- read.csv("C:\\Users\\310187796\\Desktop\\spBMD.csv")
data
attach(data)
str(data)
par(mfrow=c(1,1))
boxplot(spBMD,main="Box Plot of spBMD", col="red")
boxplot(spBMD~Smoker,main="Box Plot of spBMD", xlab="Smoker", ylab="SPBMD")
boxplot(Age,main="Box Plot of Age", col="blue")
boxplot(BMI,main="Box Plot of BMI", col="green")
boxplot(minBMI,main="Box Plot of minBMI", col="purple")
boxplot(maxBMI,main="Box Plot of maxBMI", col="blue")
plot(y, x, main="Scatterplot of SPBMD versus Age",
xlab="Age", ylab="SPBMD")
plot(y, x, main="Scatterplot of SPBMD versus BMI",
xlab="BMI", ylab="SPBMD")
plot(y, x, main="SPBMD versus minBMI",
xlab="minBMI", ylab="SPBMD", col="green")
plot(y, x, main="SPBMD versus maxBMI",
xlab="maxBMI", ylab="SPBMD", col="red")