Conservation of Momentum and Energy

(Institution)
(Name)
(Course)
(Unit)
(Unit Code)
Experiment: Momentum, Energy, and Collisions (Motion Detector)
(Professor’s Name)
(Date)

INTRODUCTION
Momentum and energy conservation can be described in terms of collisions of two carts a tracks.
Momentum conservation occurs when there is no net external force experience by the system of
the two carts while energy is only conserved when certain types of forces are exerted between
the carts. Momentum is expressed as a product of mass of the object and it velocity (Raymond A.
Serway).
Momentum=velocity∗mass
The types of collision can be classified in terms of kinetic energy; the main classification types
are elastic (kinetic energy is conserved), inelastic (kinetic energy is lost) or completely inelastic
(the object stick together after collision). Super-elastic collision condition occurs when kinetic
energy is gained. kinetic energy (KE) is expressed as product of mass and squared velocity
(Westerterp).
KE= 1
2∗mass∗Velocity2
OBJECTIVES
 To observe collisions between two carts, testing for the conservation of momentum.
 To measure the energy changes during different types of collisions.
 To classify collisions as elastic, inelastic, or completely inelastic.
MATERIALS
Computer
Vernier computer interface
Logger Pro
Two Vernier Motion Detectors
Vernier Dynamics Track
Two Vernier Dynamics Carts with magnetic and hook-and-pile strip bumpers
PRELIMINARY QUESTIONS
1. After collision ball 1 will remain in stationary position while ball 2 will move away at a
velocity that ball 1 was moving before colliding it.
2. .

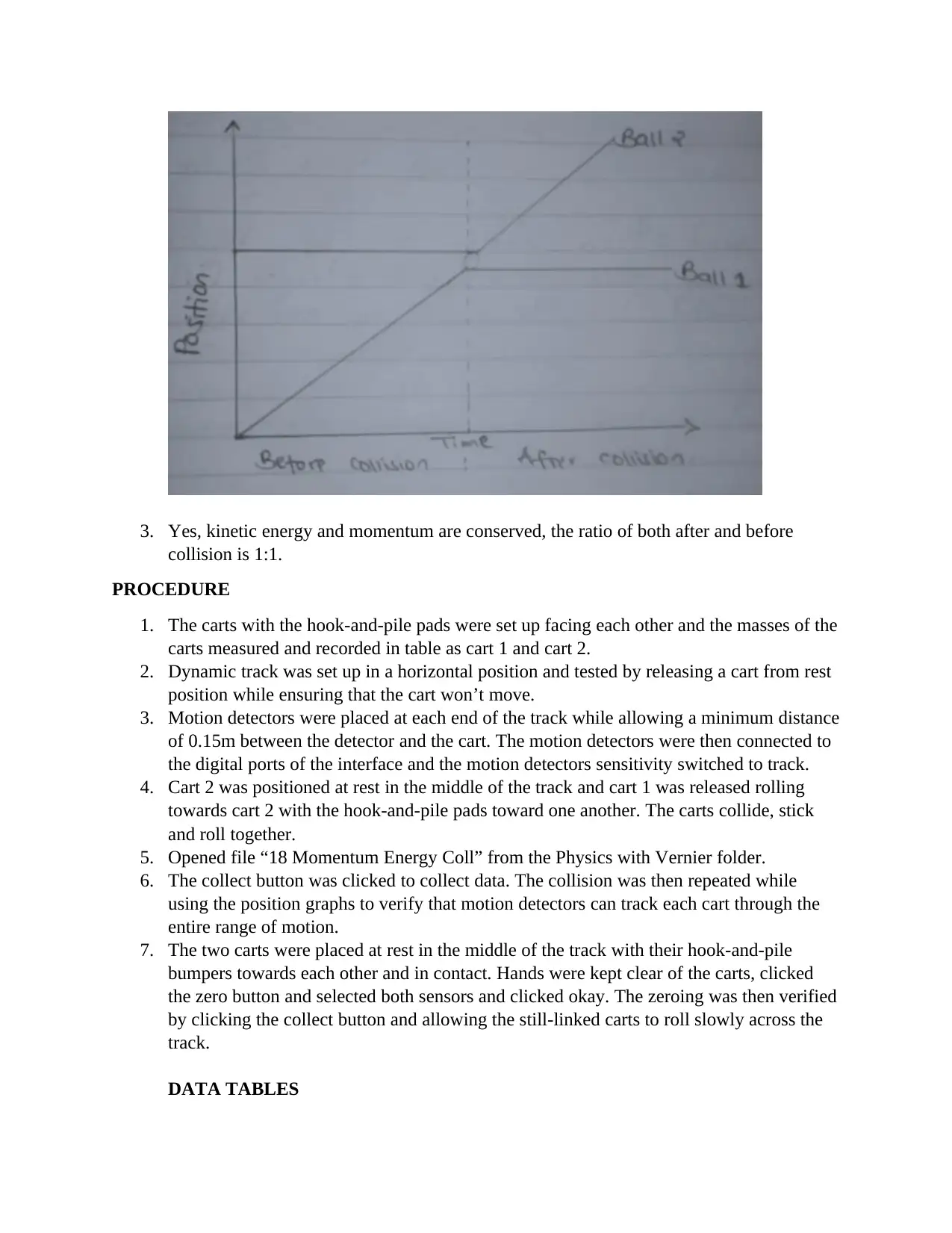
3. Yes, kinetic energy and momentum are conserved, the ratio of both after and before
collision is 1:1.
PROCEDURE
1. The carts with the hook-and-pile pads were set up facing each other and the masses of the
carts measured and recorded in table as cart 1 and cart 2.
2. Dynamic track was set up in a horizontal position and tested by releasing a cart from rest
position while ensuring that the cart won’t move.
3. Motion detectors were placed at each end of the track while allowing a minimum distance
of 0.15m between the detector and the cart. The motion detectors were then connected to
the digital ports of the interface and the motion detectors sensitivity switched to track.
4. Cart 2 was positioned at rest in the middle of the track and cart 1 was released rolling
towards cart 2 with the hook-and-pile pads toward one another. The carts collide, stick
and roll together.
5. Opened file “18 Momentum Energy Coll” from the Physics with Vernier folder.
6. The collect button was clicked to collect data. The collision was then repeated while
using the position graphs to verify that motion detectors can track each cart through the
entire range of motion.
7. The two carts were placed at rest in the middle of the track with their hook-and-pile
bumpers towards each other and in contact. Hands were kept clear of the carts, clicked
the zero button and selected both sensors and clicked okay. The zeroing was then verified
by clicking the collect button and allowing the still-linked carts to roll slowly across the
track.
DATA TABLES

Table 1

ANALYSIS
The values of momentum collected and recorded in the table was evaluated as follow.
Momentum=mass∗velocity
mass ( m )=mass of cart 1 m1 kg∧cart 2is m2 kg
velocity ( v )=cart 1 velocity ∈V 1 ( m
s )∧cart 2 velocity V 2=0 ( m
s )
Momentum of cart 1 before collison
¿ ( m1∗V 1 ) kg∗m
s
Momentum of cart 2 before collison
¿ ( m1∗V 2 )
but V 2 =0 m/s
(m¿¿ 1∗0)=0 kg . m/s ¿

After collision cart 1∧2 stick together ∧move∈the same direction
with the same velocity=V m
Momentum of cart 1 after collison
¿ ( m1∗V m ) kg∗m
s
Momentum of cart 2 after collison
¿ ( m2∗V m ) kg∗m
s
Total Momentum before collison
¿ ( Momentum of cart 1+ Momentum of cart 2 ) before collison
Total Momentum After collison
¿ ( Momentum of cart 1+ Momentum of cart 2 ) After collison
RatioTotal momentum after /before collison
¿ Total Momentum After collison
Total Momentum before collison
Solution
In order to evaluate the kinetic energy (KE) of the carts the velocity of cart 1 and cart2 before
and after collision are calculated in the following process in Microsoft Excel.
Kinetic energys before collision
KE= 1
2∗m1∗V 1
2
Velocity of cart 1before collision V 1
V 1= Momentum of cart 1 before collison
mass of cart 1
Example
m1= 516.71 g
1000 g ∗1 kg=0.51671 kg
Momentum of cart 1 before collison=0.266 kg . m
s

V 1= ( 0.266 kg . m
s )
0.51671 kg =0.5148 m
s
KE= 1
2∗0.51671 kg∗(0.5148 m
s )2
=0.06847 kg . ( m
s )2
Kinetic energy of cart 2 after collision
Velocity of cart 2before collision V 2
Cart 2 is at rest position, V 2=0 m
s
Example
m2= 510.84 g
1000 g ∗1 kg=0.51084 kg
Momentum of cart 1 before collison=0. kg . m
s
V 1= ( 0 kg . m
s )
0.51084 kg =0. m
s
KE= 1
2 0.51084 kg∗( 0. m
s )
2
=0 kg . ( m
s )
2
Kinetic energys After collision
Velocity of cart 1 After collision V 1
V m 1= Momentum of cart 1 After collison
mass of cart 1
Example
m1= 516.71 g
1000 g ∗1 kg=0.51671 kg
Momentum of cart 1 After collison=0.156 kg . m
s
V m 1= ( 0.156 kg . m
s )
0.51671 kg =0.3019 m
s
KE= 1
2∗0.51671 kg∗(0.3019 m
s )2
=0.023548 kg . ( m
s )2

Kinetic energy of cart 2 after collision
Velocity of cart 2before collision V m 2
V m 2=, Momentum of cart 2 After collison
mass of ca rt 2
Example
m2= 510.84 g
1000 g ∗1 kg=0.51084 kg
Momentum of cart 1 after collison=−0.153 kg . m
s
V m 2= (¿−0.153 kg . m
s )
0.51084 kg =−0.2995 . m
s
KE= 1
2∗0.51084 kg∗(−0.2995 m
s )2
=0.0229 kg . ( m
s )2
 Total kinetic energy before the collision
¿ Kinetic energy of cart 1before collision+Kinetic energy of cart 2 before collision
Example
= 0.068467806+0 = 0.068467806kg . ( m
s )
2
 Total kinetic energy after the collision
¿ Kinetic energy of cart 1after collision+ Kinetic energy of cart 2 after collision
Example
= 0.023548993+ 0.022912262= 0.046461255 kg . ( m
s )
2
 Ratio of the total kinetic energy after the collision ¿ thetotal
kinetic energy before the collision
= Total kinetic energy after the collision
Total kinetic energy before the collision
Example
¿
0.046461255 kg . ( m
s )
2
0.068467806 kg . ( m
s )
2 =0.67858542

Table 4: Calculated data in excel
 If the system momentum is conserved, the ratio of total momentum after the collision to
the total momentum before the collision will have a ratio of 1:1.
 When kinetic energy is conserved, the ratio of the total kinetic energy after the collision
to the total kinetic energy before the collision will have a ratio of 1:1.

 No, momentum was not conserved in my collision. In the three trials performed none of
the ratio was very close to 1.
 Yes, the kinetic energy is conserved by the completely inelastic collision since the ratio is
very close to one as seen in the last three collisions on the table.
CONCLUSION
The analysis of the experimental results proofs that both kinetic energy and the momentum of
colliding system of bodies is conserves when the total kinetic energy and momentum before
collision is equal to the momentum and kinetic energy after collision giving a ratio of 1:1.
References
Raymond A. Serway, Chris Vuille. College Physics (9th Edition). Brooks Cole, 2011.
Westerterp, Klaas R. Energy Balance in Motion. Springer-Verlag Berlin Heidelberg, 2013.