Intermediate Calculations Assignment

A 9-year bond has a yield of 8.5% and a duration of 8.489 years. If the market yield changes by 90 basis
points, what is the percentage change in the bond’s price? (Do not round intermediate calculations.
Input the amount as a positive value. Round your answer to 2 decimal places. Omit the "%" sign
in your response.)
The percentage change in the bond’s price is %.
rev: 02_24_2016_QC_CS-43398
Find the duration of a 4% coupon bond making annual coupon payments if it has 3 years until maturity
and has a yield to maturity of 4%. What is the duration if the yield to maturity is 6%? Note: The face value
of the bond is $1,000. (Do not round intermediate calculations. Round your answers to 3 decimal
places.)
Duration
4% YTM years
6% YTM years
You will be paying $9,200 a year in tuition expenses at the end of the next 2 years. Bonds currently yield
6%.
a. What is the present value and duration of your obligation? (Do not round intermediate
calculations. Round "Present value" to 2 decimal places and "Duration" to 4 decimal places.
Omit the "$" sign in your response.)
Present value $
Duration years
b. What maturity zero-coupon bond would immunize your obligation? (Do not round intermediate
calculations. Round "Duration" to 4 decimal places and "Face value" to 2 decimal
places.Omit the "$" sign in your response.)
Duration years
70.42
2.886
2.833
16867.2
1.4854
1.4854

Face value $
Suppose you buy a zero-coupon bond with value and duration equal to your obligation.
c-1. Now suppose that rates immediately increase to 8%. What happens to your net position, that is, to
the difference between the value of the bond and that of your tuition obligation? (Do not round
intermediate calculations. Input the amount as a positive value. Round your answer to 2
decimal places. Omit the "$" sign in your response.)
Net position in value by $
c-2. Now suppose that rates immediately falls to 4%. What happens to your net position, that is, to the
difference between the value of the bond and that of your tuition obligation? (Do not round
intermediate calculations. Input the amount as a positive value. Round your answer to 2
decimal places. Omit the "$" sign in your response.)
Net position in value by $
A newly issued bond has a maturity of 10 years and pays a 7.6% coupon rate (with coupon payments
coming once annually). The bond sells at par value.
a. What are the convexity and the duration of the bond? Use the formula for convexity in footnote
7. (Round your answers to 3 decimal places.)
Convexity
Duration years
b. Find the actual price of the bond assuming that its yield to maturity immediately increases from 7.6%
to 8.6% (with maturity still 10 years). Assume a par value of 100. (Round your answer to 2 decimal
places. Omit the "%" sign in your response.)
Actual price of the bond %
c. What percentage price change would be predicted by the duration rule What is the percentage error
of that rule? (Negative answers should be indicated by a minus sign. Round your answers to 2
decimal places. Omit the "%" sign in your response.)
18392.2
decreases 0.72
decreases 0.79
62.246
7.352
6.62

Percentage price change %
Percentage error %
d. What percentage price change would be predicted by the duration-with-convexity rule What is the
percentage error of that rule? (Negativeanswers should be indicated by a minus sign. Round
your answers to 2 decimal places. Omit the "%" sign in your response.)
Percentage price change %
Percentage error %
rev: 03_31_2015_QC_CS-12296
The common stock of the P.U.T.T. Corporation has been trading in a narrow price range for the past
month, and you are convinced it is going to break far out of that range in the next 6 months. You do not
know whether it will go up or down, however. The current price of the stock is $90 per share, and the
price of a 6-month call option at an exercise price of $90 is $8.69.
a. If the risk-free interest rate is 7% per year, what must be the price of a 6-month put option on P.U.T.T.
stock at an exercise price of $90? (The stock pays no dividends.) (Do not round intermediate
calculations. Round your answer to 2 decimal places. Omit the "$" sign in your response.)
Put-call parity $
b. What would be a simple options strategy to exploit your conviction about the stock price’s future
movements? How far would it have to move in either direction for you to make a profit on your initial
investment? (Round your intermediate calculations and final answer to 2 decimal places. Omit
the "$" sign in your response.)
Total cost of the straddle $
6.83
0.21
6.52
0.01
4.50
13.84

You buy a share of stock, write a 1-year call option with X = $30, and buy a 1-year put option with X =
$30. Your net outlay to establish the entire portfolio is $28.6. The stock pays no dividends.
What is the risk-free interest rate? (Do not round intermediate calculations. Round your answer to 2
decimal places. Omit the "$"sign in your response.)
Risk-free rate %
A call option with X = $47 on a stock currently priced at S = $52 is selling for $11. Using a volatility
estimate of σ = 0.24, you find that N(d1) = 0.7859 and N(d2) = 0.7493. The risk-free interest rate is zero.
Is the implied volatility based on the option price more or less than 0.24?
rev: 11_25_2016_QC_CS-70532
Less than 0.24
Greater than 0.24
The hedge ratio of an at-the-money call option on IBM is 0.44. The hedge ratio of an at-the-money put
option is -0.56. What is the hedge ratio of an at-the-money straddle position on IBM? (Negative answer
should be indicated by a minus sign. Round your answer to 2 decimal place.)
Hedge ratio
A collar is established by buying a share of stock for $62, buying a 6−month put option with exercise
price $56, and writing a 6−month call option with exercise price $68. On the basis of the volatility of the
stock, you calculate that for a strike price of $56 and expiration of 6 months, N(d1) = .7247, whereas for
the exercise price of $68, N(d1) = 0.6564.
a. What will be the gain or loss on the collar if the stock price increases by $1? (Round your answer
to 2 decimal places. Omit the "$" sign in your response.)
Collar by
4.90
-0.12
gain 0.07

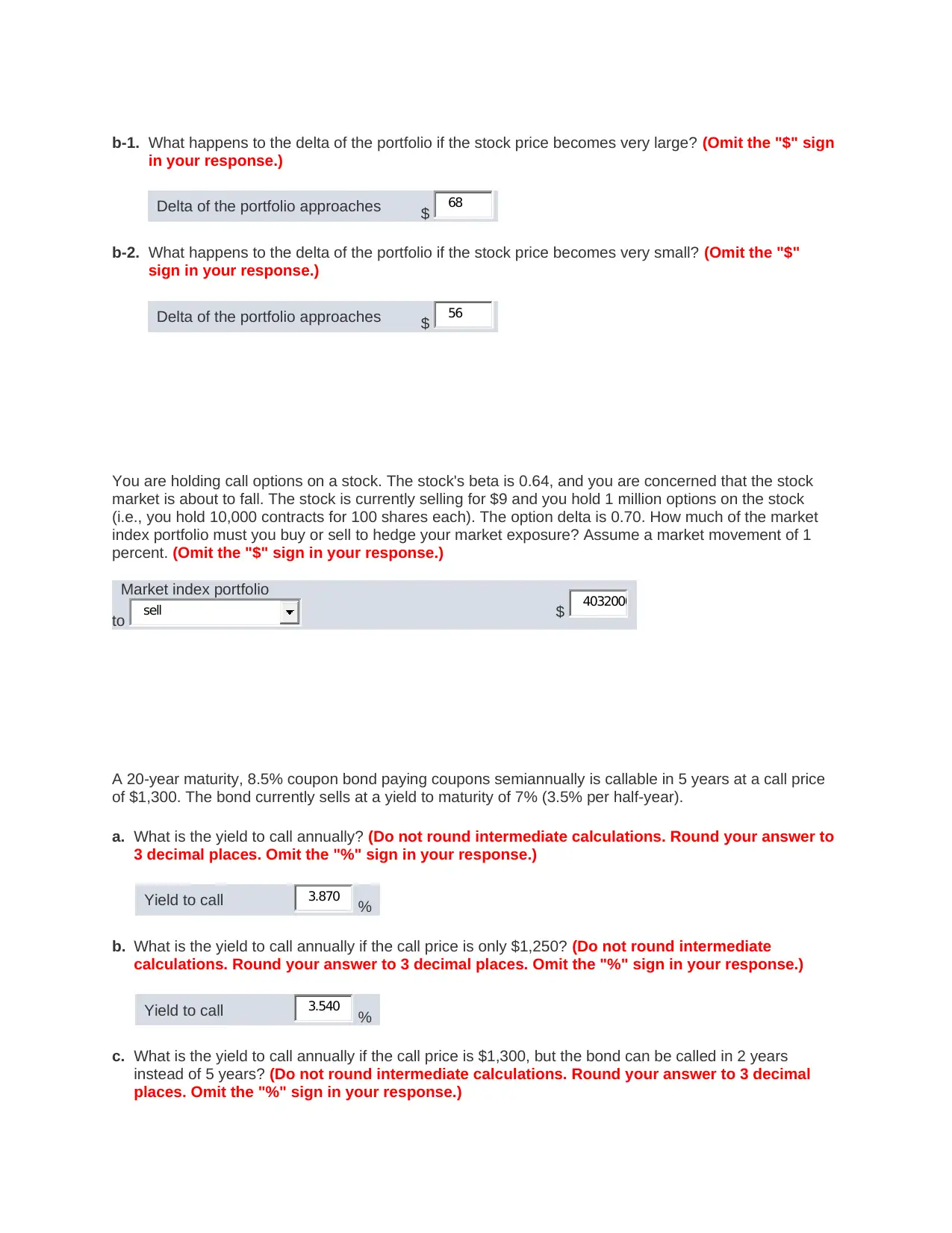
b-1. What happens to the delta of the portfolio if the stock price becomes very large? (Omit the "$" sign
in your response.)
Delta of the portfolio approaches $
b-2. What happens to the delta of the portfolio if the stock price becomes very small? (Omit the "$"
sign in your response.)
Delta of the portfolio approaches $
You are holding call options on a stock. The stock's beta is 0.64, and you are concerned that the stock
market is about to fall. The stock is currently selling for $9 and you hold 1 million options on the stock
(i.e., you hold 10,000 contracts for 100 shares each). The option delta is 0.70. How much of the market
index portfolio must you buy or sell to hedge your market exposure? Assume a market movement of 1
percent. (Omit the "$" sign in your response.)
Market index portfolio
to $
A 20-year maturity, 8.5% coupon bond paying coupons semiannually is callable in 5 years at a call price
of $1,300. The bond currently sells at a yield to maturity of 7% (3.5% per half-year).
a. What is the yield to call annually? (Do not round intermediate calculations. Round your answer to
3 decimal places. Omit the "%" sign in your response.)
Yield to call %
b. What is the yield to call annually if the call price is only $1,250? (Do not round intermediate
calculations. Round your answer to 3 decimal places. Omit the "%" sign in your response.)
Yield to call %
c. What is the yield to call annually if the call price is $1,300, but the bond can be called in 2 years
instead of 5 years? (Do not round intermediate calculations. Round your answer to 3 decimal
places. Omit the "%" sign in your response.)
68
56
sell 4032000
3.870
3.540

Yield to call %
A firm recently issued convertible bonds with a face value of $1,000 and a conversion price of 100.
The bonds were issued at a price of $925.
Similar non-convertible bonds (same coupon, risk and maturity) are currently trading for $730.
What is the value of the call option contained in the bond on a per share basis? $
(provide your answer rounded to two decimals)
A firm has $100 face value zero coupon bonds maturing in 15 years.
The yield to maturity on similar maturity treasuries is 3%. There is a 3% risk premium on the firm's
bonds, and a 2% default premium on the bonds.
If the firm defaults, the bonds will only pay 0 (zero) cents on the dollar.
What is the expected return on the bond? %
What is the promised return on the bond? %
What is the price of the bond?
(round your answer to 2 decimals)
What is the probability of default? (Enter as a decimal between 0 and 1, not a percent,
rounded to 2 decimals)
An investment bank recently purchased a zero coupon convertible bond.
The bond has a conversion ratio of 50 (and a par of $1,000). The bond matures in 7 years.
4.650
7.30
107.89
34.59
48.10
0.32

The stock is currently trading for $81. You've already computed N(d1)=0.54 and N(d2)=0.37.
A hedge fund believes that the bond is overpriced.
The fund does not want to hold the bond to maturity, but instead would like to profit in the short run
when it believes that the bond's mispricing will be corrected. Assume that the stock pays no
dividends.
Fill in the strategy that the hedge fund should pursue:
The fund should (enter: long or short) shares per bond. (enter number of shares
rounded to an integer)
Short 20