International Finance Management: Methods and Analysis

This document provides an overview of international finance management, discussing the financial management methods and their relevance. It includes calculations of net present value, standard deviation, and allocation of funds for achieving optimum return. The document also explores the concept of NPV technique being superior to IRR and provides insights into project ranking and capital allocation.

INTERNATIONAL FINANCE
MANAGEMENT

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................3
Question: 1...................................................................................................................................3
Question 2....................................................................................................................................5
Question 3....................................................................................................................................8
a) Calculation of Net Present Value of four projects...................................................................8
c) Allocation of funds for achieving optimum return in terms of getting highest Net Present
Value............................................................................................................................................9
CONCLUSION..............................................................................................................................12
REFERENCES..............................................................................................................................13

INTRODUCTION
The file is on international finance management. It talks about the financial management
methods which can be of help for the company’s investment decisions and management of
wealth in the right direction. It speaks about the company’s choice of taking the best investment
decision and talks of the business objectives of company and the decision of how the company is
using the financial resources of the company. The relevance of these methods has been shown
with calculation and interpretation has been done.
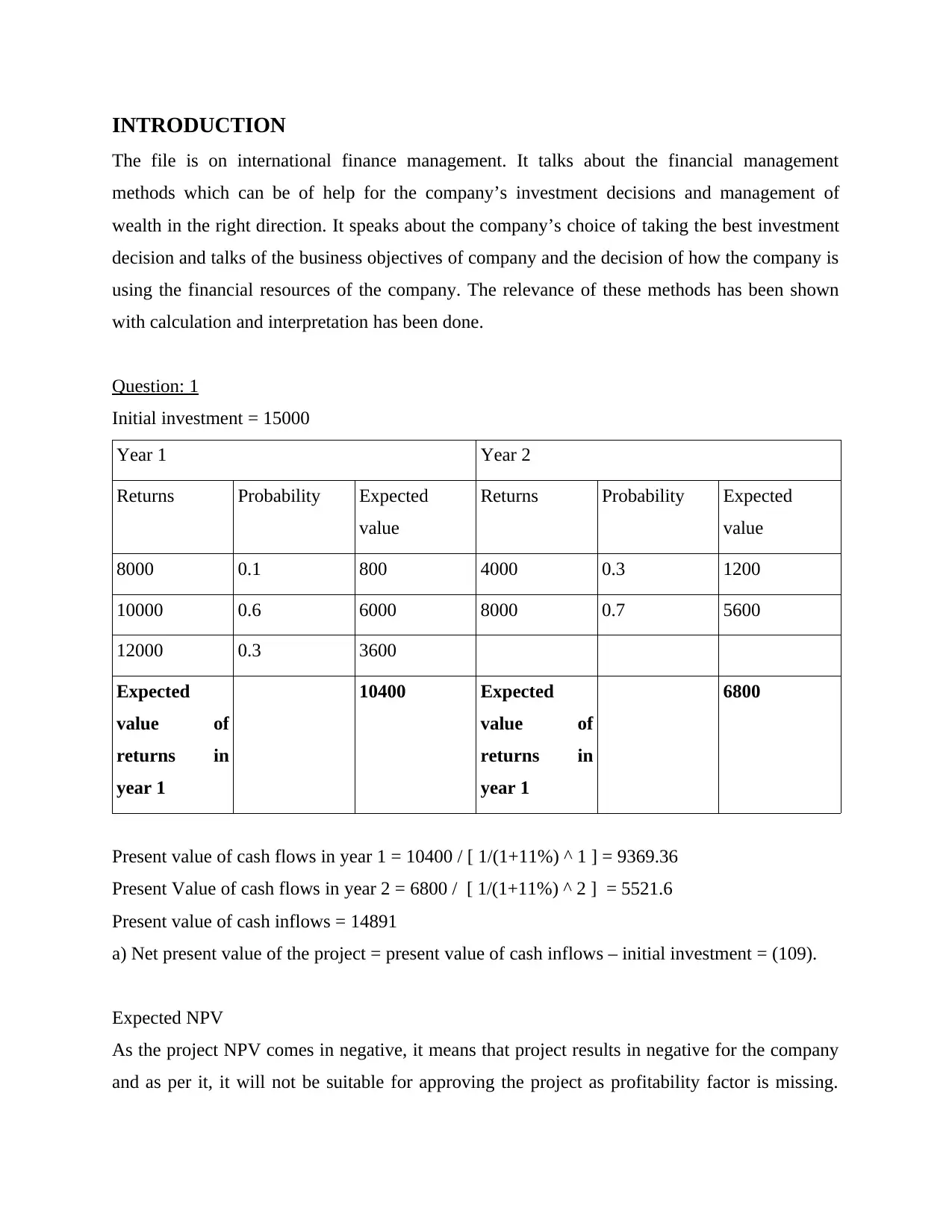
Question: 1
Initial investment = 15000
Year 1 Year 2
Returns Probability Expected
value
Returns Probability Expected
value
8000 0.1 800 4000 0.3 1200
10000 0.6 6000 8000 0.7 5600
12000 0.3 3600
Expected
value of
returns in
year 1
10400 Expected
value of
returns in
year 1
6800
Present value of cash flows in year 1 = 10400 / [ 1/(1+11%) ^ 1 ] = 9369.36
Present Value of cash flows in year 2 = 6800 / [ 1/(1+11%) ^ 2 ] = 5521.6
Present value of cash inflows = 14891
a) Net present value of the project = present value of cash inflows – initial investment = (109).
Expected NPV
As the project NPV comes in negative, it means that project results in negative for the company
and as per it, it will not be suitable for approving the project as profitability factor is missing.

Reason behind negative NPV is prominent reduction in value expected of returns which are
derived from project being compared to year 1. The project which is existing does not allow the
business for gaining the capital value as it invests against the project respective. In context of
each project it is necessary that the business gets more value than invested (Zore and et.al.,
2018). The rule which is present and acceptable is that total inflow in future as against the project
should be more than the total investment company is incurring about the project.
b) The standard deviation of NPV
Year 1
Returns
(X)
D = (X –
Expected value)
D2 Probability Probability * D2
8000 -2400 5760000 0.1 576000
10000 -400 160000 0.6 96000
12000 1600 2560000 0.3 768000
Variance of returns in year 1 = σ2 1440000
Standard deviation of returns in year 1 = square root of σ2 = σ = 1200.
By calculation of standard deviation, different scenarios of cash flows possible from project of
year 1, the value is coming out to be 1200, indicating that different events which are related of
cash flow deviate from return expected of project in year 1 by 1200.
Year 2
Returns (X) D = (X –
Expected value)
D2 Probability Probability * D2
4000 -2800 7840000 0.3 2352000
8000 1200 1440000 0.7 1008000
Variance of returns in year 2 = σ2 3360000
Standard deviation of returns in year 2 = square root of σ2 = σ 1833

Standard deviation which is of different possible results of cash flow from year 2 project has
come to be 1833, which indicates that there are scenarios which are different of cash flow in year
2 are deviating from expected return from project of year 2 by 1833.
Question 2
Calculation of net present value of RJW's estimates
Time Net cash flows Present value factor @
14%
Present value of cash
flows
0 -900 1 -900
1 130 0.88 114.01
2 145 0.77 111.51
3 150 0.68 101.25
4 130 0.59 76.96
5 150 0.52 77.85
Net present value -418.43
Net present value of the proposal stands to be negative. Thus this project cannot be given
approval as it is not producing appropriate results which decision making entity has made. It is
crucial for undertaking to make investment in the right direction which can generate investment
for the company (Zore and et.al., 2018).
Calculation of net present value for a more optimistic forecast
Time Net cash flows Present value factor @
14%
Present value of cash
flows
0 -900 1 -900
1 260 0.88 228.02
2 276.6 0.77 212.71

3 283.33 0.68 191.25
4 271 0.59 160.43
5 280 0.52 145.32
Net present value 37.73
Calculation of net present value for a pessimistic forecast
Time Net cash flows Present value factor @
14%
Present value of cash
flows
0 -900 1 -900
1 96.67 0.88 84.78
2 111.7 0.77 85.9
3 116.67 0.68 78.75
4 -21 0.59 -12.43
5 20 0.52 10.38
Net present value -652.62
Calculation of expected NPV
NPV in different scenarios Probability Expected value
-418.43 0.5 -209.21
37.73 0.3 11.32
-652.62 0.2 -130.52
Expected NPV -328.42
Calculation of standard deviation of NPV
Events NPV D = (NPV – Expected D2 P = PD2

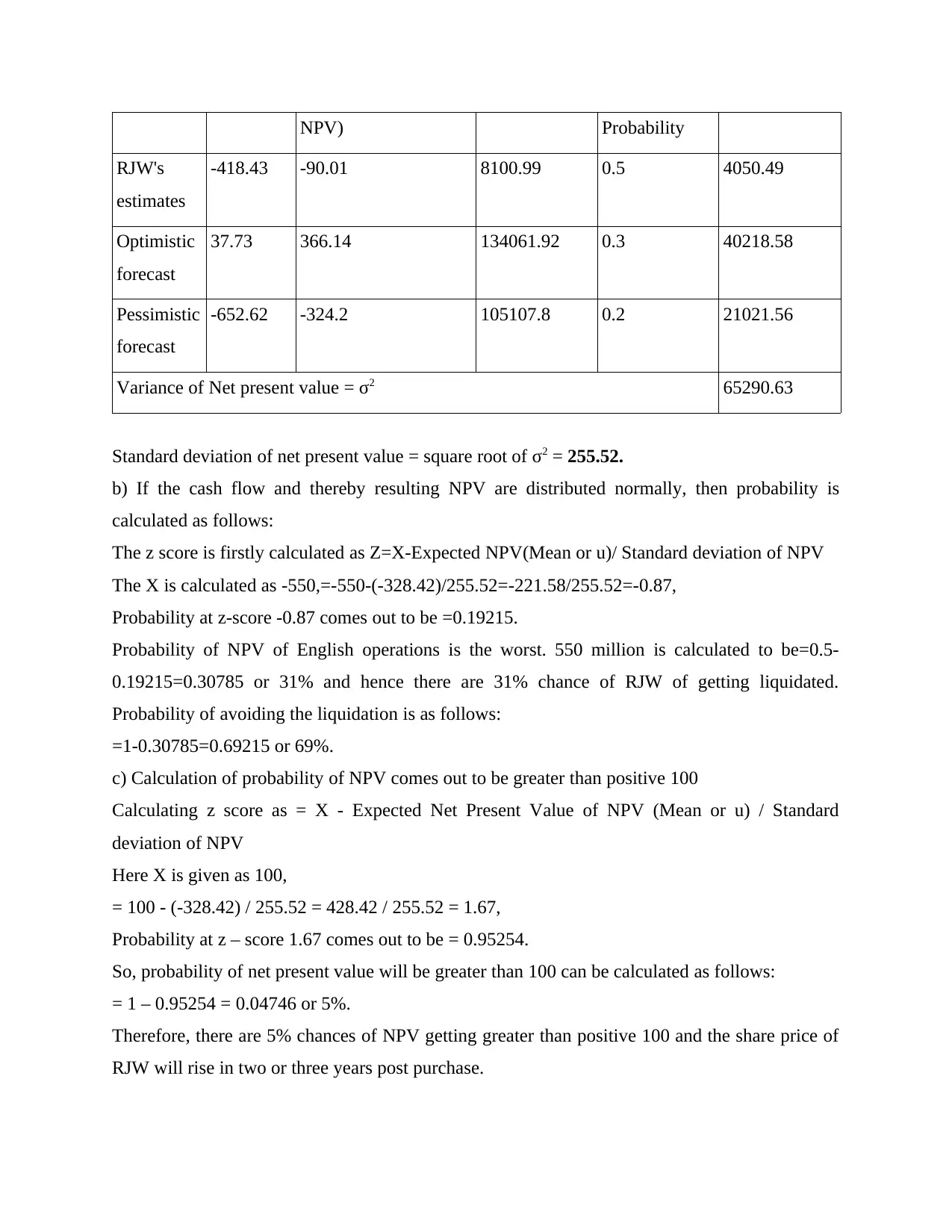
NPV) Probability
RJW's
estimates
-418.43 -90.01 8100.99 0.5 4050.49
Optimistic
forecast
37.73 366.14 134061.92 0.3 40218.58
Pessimistic
forecast
-652.62 -324.2 105107.8 0.2 21021.56
Variance of Net present value = σ2 65290.63
Standard deviation of net present value = square root of σ2 = 255.52.
b) If the cash flow and thereby resulting NPV are distributed normally, then probability is
calculated as follows:
The z score is firstly calculated as Z=X-Expected NPV(Mean or u)/ Standard deviation of NPV
The X is calculated as -550,=-550-(-328.42)/255.52=-221.58/255.52=-0.87,
Probability at z-score -0.87 comes out to be =0.19215.
Probability of NPV of English operations is the worst. 550 million is calculated to be=0.5-
0.19215=0.30785 or 31% and hence there are 31% chance of RJW of getting liquidated.
Probability of avoiding the liquidation is as follows:
=1-0.30785=0.69215 or 69%.
c) Calculation of probability of NPV comes out to be greater than positive 100
Calculating z score as = X - Expected Net Present Value of NPV (Mean or u) / Standard
deviation of NPV
Here X is given as 100,
= 100 - (-328.42) / 255.52 = 428.42 / 255.52 = 1.67,
Probability at z – score 1.67 comes out to be = 0.95254.
So, probability of net present value will be greater than 100 can be calculated as follows:
= 1 – 0.95254 = 0.04746 or 5%.
Therefore, there are 5% chances of NPV getting greater than positive 100 and the share price of
RJW will rise in two or three years post purchase.

Question 3
a) Calculation of Net Present Value of four projects
Project A
Time in year Cash flows Present value factor
@ 10%
Present value of cash
flows
0 -500000 1 -500000
1 600000 0.909 545400
Net present value of cash flows from project A 45400
Project B
0 -200000 1 -200000
1 200000 0.909 181800
2 150000 0.826 123900
Net present value of cash flows from project B 105700
Project C
0 -700000 1 -700000
1 0 0.909 0
2 1000000 0.826 826000
Net present value of cash flows from project C 126000
Project D
0 -150000 1 -150000
1 60000 0.909 54540
2 60000 0.826 49560
3 60000 0.751 45060
4 60000 0.683 40980
Net present value of cash flows from project D 40140
Ranking projects on the basis of calculated NPVs
Projects NPV Rank
A 45400 3
B 105700 2
C 126000 1

D 40140 4
b) Reasons for regarding NPV technique which is superior to IRR
a) The reason for which NPV can be considered superior over IRR is it can rank projects with
cash flows which are uneven on different period of time which is required to identify the most
suitable investment.
b) The reason for NPV being considered a better technique over the IRR is it lets discounting
various years’ cash flows at different discount rates and is also without problems which makes
the option better than IRR (Creemers, 2018).
c) Net present value technique allows the business for identification of expected total benefit
against the initial investment made by it. Investor can analyse the expected total outcome in
same manner as initial investment is identified by the concerned investor. Looking from other
perspective, internal rate of return provide return which can be a bit complex to understand and
compute for some investors.
d) The flexibility which NPV provides is that even if the multiple discount rates are given they
can be handled through NPV which is not possible in case of IRR.
e) In context of decision-making in investment the scale of project and investment level requires
in the project is crucial element which can affect the decision-making technique. Net present
value technique covering up the aspect and also involving the inflow level expected belonging to
the whole life of project.
f) IRR also assumes that reinvestment and the discounting rate of return are the same concept
however, NPV method says that differentiation has been understood in clear terms. Speaking of
financial management each single concept puts a direct impact.
g) In case of NPV, rate of borrowing is assumed as well as coming close to market rate is not
absolutely impractical and can certainly come of use.
c) Allocation of funds for achieving optimum return in terms of getting highest Net Present
Value
Initial capital available for project investment = £700000
Calculation of weights
Project NPV Weights

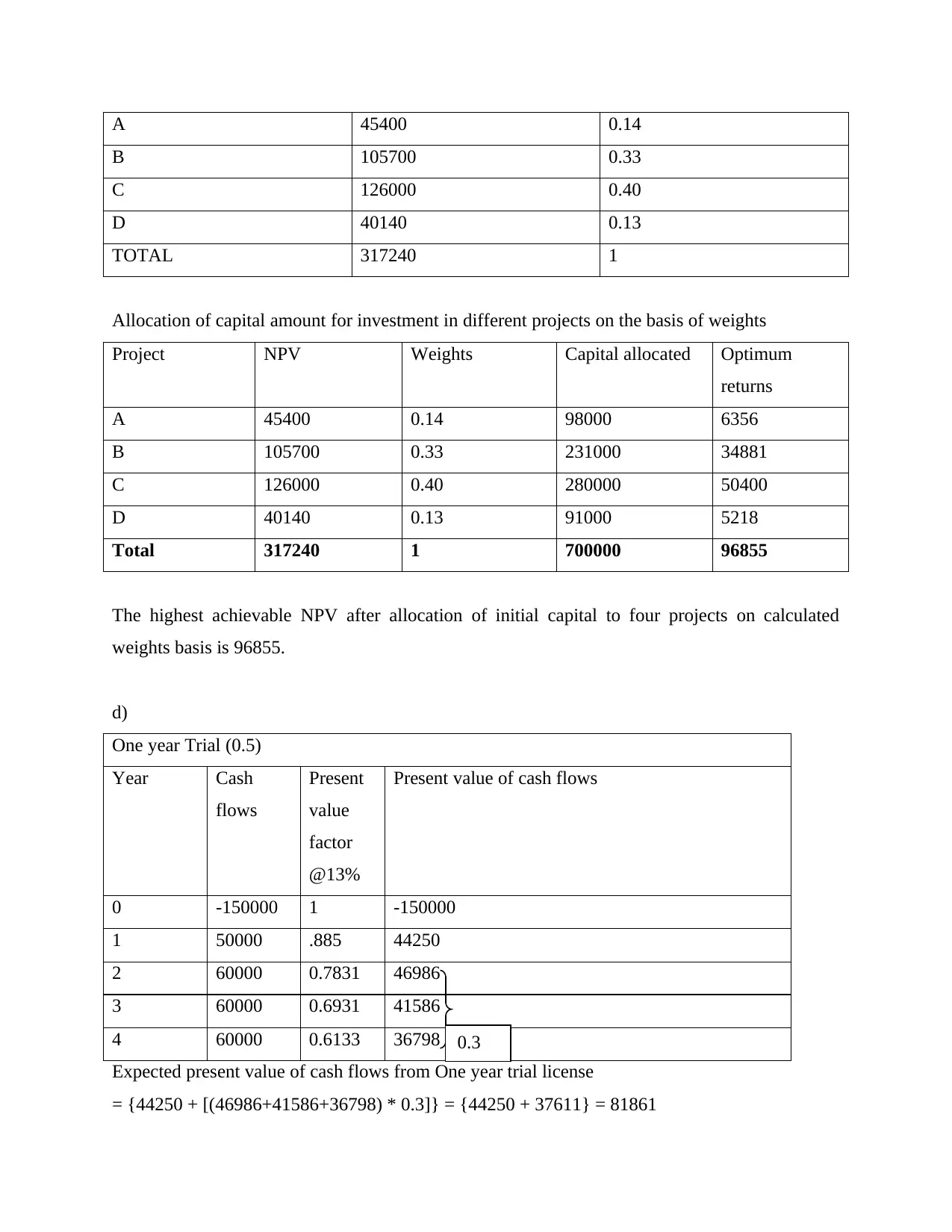
A 45400 0.14
B 105700 0.33
C 126000 0.40
D 40140 0.13
TOTAL 317240 1
Allocation of capital amount for investment in different projects on the basis of weights
Project NPV Weights Capital allocated Optimum
returns
A 45400 0.14 98000 6356
B 105700 0.33 231000 34881
C 126000 0.40 280000 50400
D 40140 0.13 91000 5218
Total 317240 1 700000 96855
The highest achievable NPV after allocation of initial capital to four projects on calculated
weights basis is 96855.
d)
One year Trial (0.5)
Year Cash
flows
Present
value
factor
@13%
Present value of cash flows
0 -150000 1 -150000
1 50000 .885 44250
2 60000 0.7831 46986
3 60000 0.6931 41586
4 60000 0.6133 36798
Expected present value of cash flows from One year trial license
= {44250 + [(46986+41586+36798) * 0.3]} = {44250 + 37611} = 81861
0.3

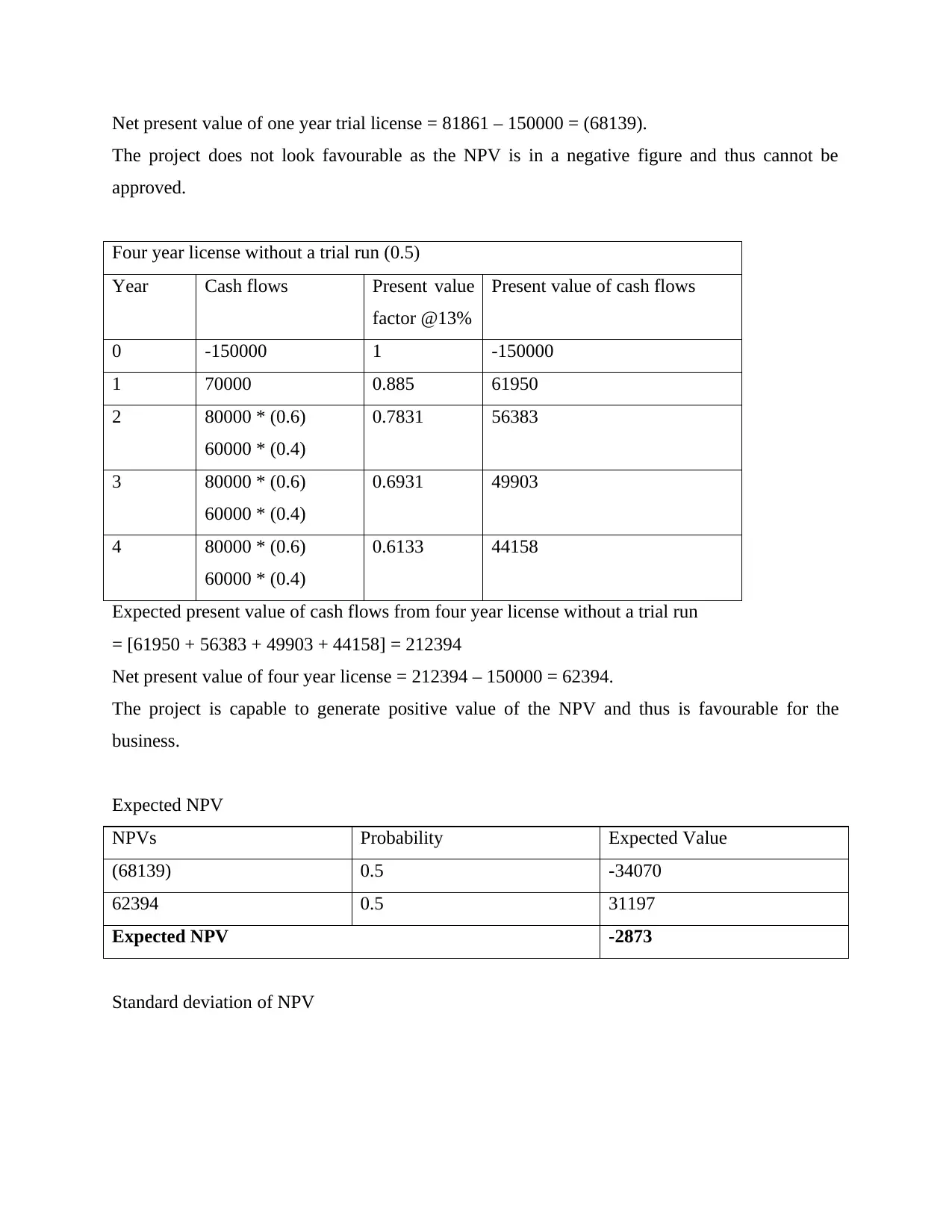
Net present value of one year trial license = 81861 – 150000 = (68139).
The project does not look favourable as the NPV is in a negative figure and thus cannot be
approved.
Four year license without a trial run (0.5)
Year Cash flows Present value
factor @13%
Present value of cash flows
0 -150000 1 -150000
1 70000 0.885 61950
2 80000 * (0.6)
60000 * (0.4)
0.7831 56383
3 80000 * (0.6)
60000 * (0.4)
0.6931 49903
4 80000 * (0.6)
60000 * (0.4)
0.6133 44158
Expected present value of cash flows from four year license without a trial run
= [61950 + 56383 + 49903 + 44158] = 212394
Net present value of four year license = 212394 – 150000 = 62394.
The project is capable to generate positive value of the NPV and thus is favourable for the
business.
Expected NPV
NPVs Probability Expected Value
(68139) 0.5 -34070
62394 0.5 31197
Expected NPV -2873
Standard deviation of NPV

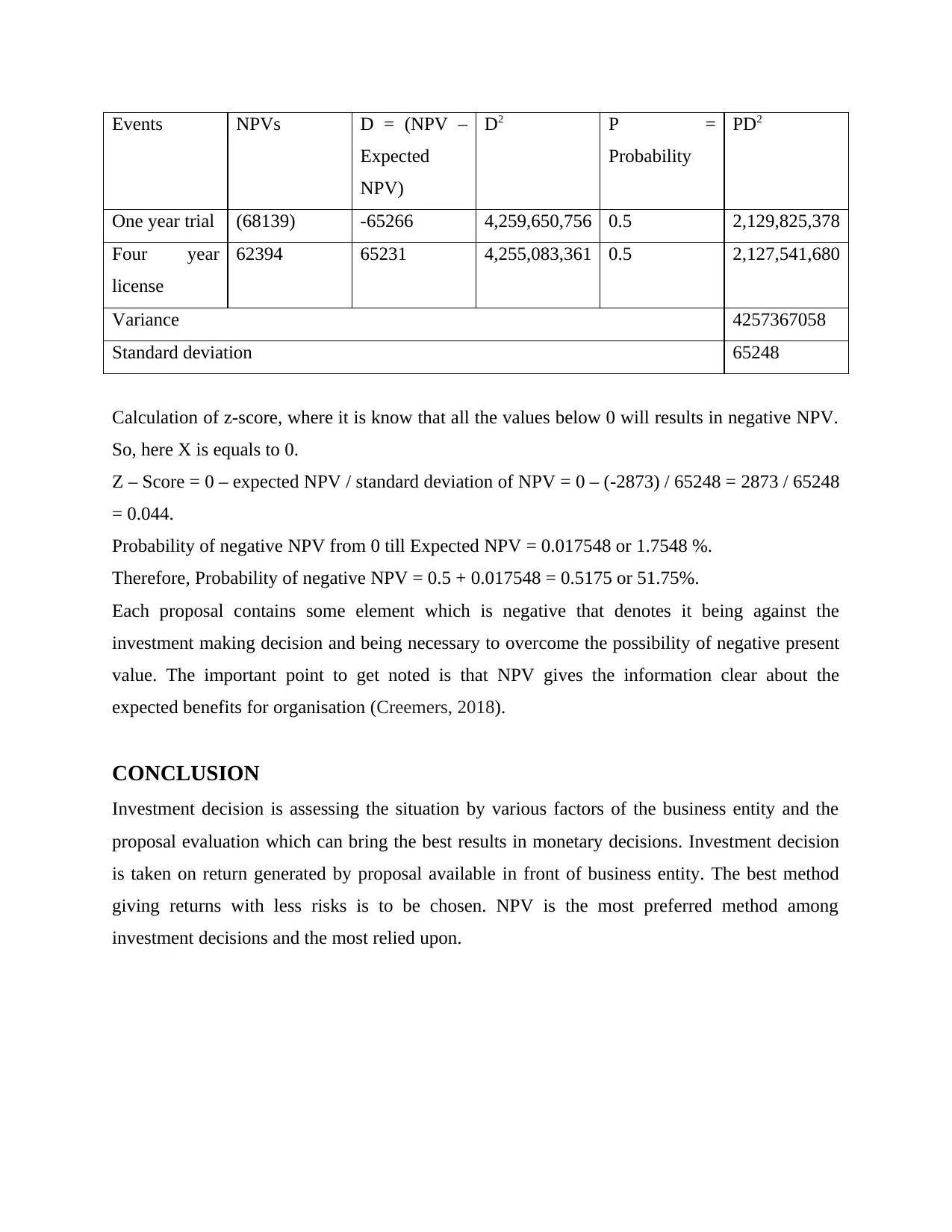
Events NPVs D = (NPV –
Expected
NPV)
D2 P =
Probability
PD2
One year trial (68139) -65266 4,259,650,756 0.5 2,129,825,378
Four year
license
62394 65231 4,255,083,361 0.5 2,127,541,680
Variance 4257367058
Standard deviation 65248
Calculation of z-score, where it is know that all the values below 0 will results in negative NPV.
So, here X is equals to 0.
Z – Score = 0 – expected NPV / standard deviation of NPV = 0 – (-2873) / 65248 = 2873 / 65248
= 0.044.
Probability of negative NPV from 0 till Expected NPV = 0.017548 or 1.7548 %.
Therefore, Probability of negative NPV = 0.5 + 0.017548 = 0.5175 or 51.75%.
Each proposal contains some element which is negative that denotes it being against the
investment making decision and being necessary to overcome the possibility of negative present
value. The important point to get noted is that NPV gives the information clear about the
expected benefits for organisation (Creemers, 2018).
CONCLUSION
Investment decision is assessing the situation by various factors of the business entity and the
proposal evaluation which can bring the best results in monetary decisions. Investment decision
is taken on return generated by proposal available in front of business entity. The best method
giving returns with less risks is to be chosen. NPV is the most preferred method among
investment decisions and the most relied upon.

REFERENCES
Books and journals
Zore, Ž., Čuček, L., Širovnik, D., Pintarič, Z.N. and Kravanja, Z., 2018. Maximizing the
sustainability net present value of renewable energy supply networks. Chemical
Engineering Research and Design, 131, pp.245-265.
Thiruvady, D., Blum, C. and Ernst, A.T., 2019, January. Maximising the net present value of
project schedules using CMSA and parallel ACO. In International Workshop on Hybrid
Metaheuristics (pp. 16-30). Springer, Cham.
Creemers, S., 2018. Moments and distribution of the net present value of a serial
project. European Journal of Operational Research, 267(3), pp.835-848.
Peymankar, M., Davari, M. and Ranjbar, M., 2021. Maximizing the expected net present value in
a project with uncertain cash flows. European Journal of Operational Research.
Sim, T. and Wright, R.H., 2017. Stock valuation using the dividend discount model: An internal
rate of return approach. In Growing Presence of Real Options in Global Financial
Markets. Emerald Publishing Limited.
Santandrea, M., Sironi, A., Grassi, L. and Giorgino, M., 2017. Concentration risk and internal
rate of return: Evidence from the infrastructure equity market. International Journal of
Project Management, 35(3), pp.241-251.
Chandra, P., 2017. Investment analysis and portfolio management. McGraw-hill education.
Mauleón, I. and Hamoudi, H., 2017. Photovoltaic and wind cost decrease estimation:
Implications for investment analysis. Energy, 137, pp.1054-1065.

Online
Author surname, First letter of name., 2020 [Online]. Available through: <online-website-link>
1