Assignment on Polynomial Interpolation and Bisection Method Solutions

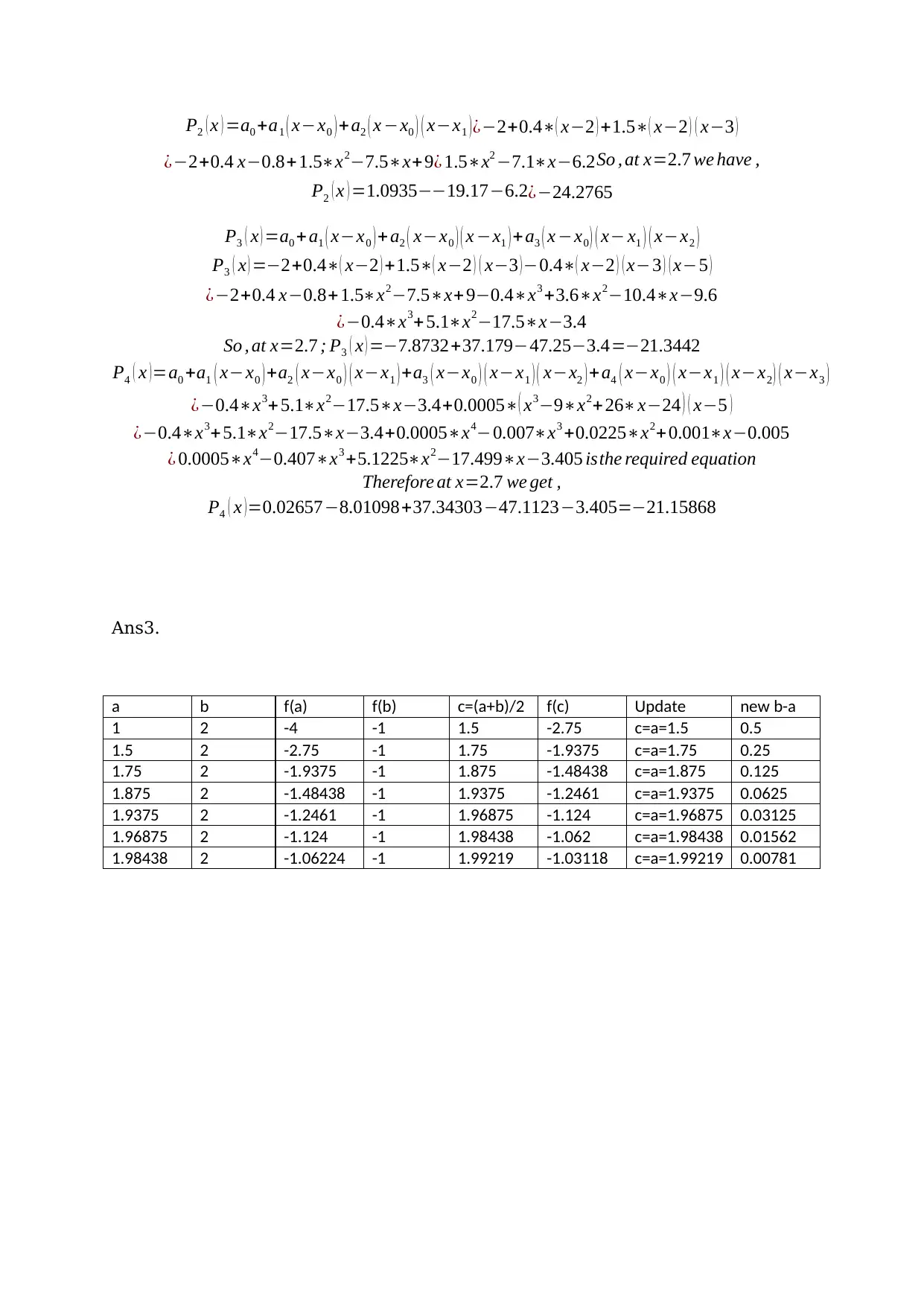
This document provides solutions to a math assignment. The first part addresses polynomial interpolation, including finding linear, quadratic, and cubic interpolation polynomials using provided nodes. The second part focuses on using given centers and coefficients to find Newton polynomials and...Read More

Ans 1.
(a)
y= y0+ ( y1− y0 ) x−x0
x1−x0
y=−1+ 1∗x+1
1 y=−1+ x +1=x y=x
(b)
f ( x )=f ( x2 ) + ( x −x2 ) ( f ( x3 )−f ( x1 ) )
2∗∆ x + ( x−x2 )2
[ f ( x1 )−2∗f ( x2 ) +f ( x3 ) ]
2∗∆ x2
f ( x ) =0+ ( x −0 ) ( 1+1 )
2 + x2 [ −1−0+1 ]
2 f ( x ) =x
(c)
Let ,f ( x )=a∗x3 +b∗x2+c∗x +d So ,−1=−a+b−c +d0=d1=a+b+ c+d 32=8 a+4 b+2 c+ d
−1=−a+b−c1=a+b+ c Adding we get ,0=−a+ b−c+ a+b+ c=2∗b¿ , b=0So , we get
−1=−a−c 32=8∗a+2∗cSo ,−8=−8 a−8 c Adding the previous two equations we get ,
32−8=8 a+2 c−8 a−8 c24=−6 c c=−4So ,1=a+0−4 +0a=5 So , we get theequation as
f ( x )=5∗x3−4∗x
(d)
y= y0+ ( y1− y0 ) x−x0
x1−x0
¿ , y=1+ ( 32−1 ) ( x−1 )
1 y=1+31 x−31 y=31 x−30
(e)
f ( x )=f ( x2 ) + ( x −x2 ) ( f ( x3 )−f ( x1 ) )
2∗∆ x + ( x−x2 )2
[ f ( x1 )−2∗f ( x2 ) +f ( x3 ) ]
2∗∆ x2
f ( x ) =1+ ( x−1 ) ( 32−1 )
2 + ( x−1 ) 2 [ 0−2∗1+32 ]
2 f ( x ) =1+ 31∗ ( x −1 )
2 + ( x−1 ) 2 30
2
f ( x ) =1+ 31∗ ( x −1 )
2 +15∗( x−1 ) 2
Ans 2.
P1 ( x ) =a0 +a1 ( x−x0 ) P1 ( x ) =−2+0.4 ( x−2 ) P1 ( x ) =−2+0.4 x−0.8 P1 ( x ) =−2.8+0.4 x
So , at x=2.7P1 ( x ) =−2.8+1.08=−1.72

P2 ( x ) =a0 +a1 ( x−x0 ) + a2 ( x −x0 ) ( x−x1 )¿−2+0.4∗( x−2 ) +1.5∗( x−2 ) ( x−3 )
¿−2+0.4 x−0.8+1.5∗x2−7.5∗x+ 9¿ 1.5∗x2 −7.1∗x−6.2 So , at x=2.7 we have ,
P2 ( x ) =1.0935−−19.17−6.2¿−24.2765
P3 ( x ) =a0 + a1 ( x−x0 ) + a2 ( x−x0 ) ( x −x1 ) +a3 ( x −x0 ) ( x− x1 ) ( x−x2 )
P3 ( x ) =−2+0.4∗( x−2 ) +1.5∗( x−2 ) ( x−3 )−0.4∗( x−2 ) ( x−3 ) ( x−5 )
¿−2+0.4 x−0.8+ 1.5∗x2−7.5∗x+9−0.4∗x3 +3.6∗x2−10.4∗x−9.6
¿−0.4∗x3+ 5.1∗x2−17.5∗x−3.4
So , at x=2.7 ; P3 ( x ) =−7.8732+37.179−47.25−3.4=−21.3442
P4 ( x ) =a0 +a1 ( x−x0 ) +a2 ( x−x0 ) ( x−x1 ) +a3 ( x−x0 ) ( x−x1 ) ( x−x2 ) +a4 ( x−x0 ) ( x−x1 ) ( x−x2 ) ( x−x3 )
¿−0.4∗x3+ 5.1∗x2−17.5∗x−3.4+0.0005∗( x3−9∗x2+26∗x−24 ) ( x−5 )
¿−0.4∗x3+5.1∗x2−17.5∗x−3.4+0.0005∗x4−0.007∗x3 +0.0225∗x2+ 0.001∗x−0.005
¿ 0.0005∗x4−0.407∗x3 +5.1225∗x2−17.499∗x−3.405 isthe required equation
Therefore at x=2.7 we get ,
P4 ( x )=0.02657−8.01098+37.34303−47.1123−3.405=−21.15868
Ans3.
a b f(a) f(b) c=(a+b)/2 f(c) Update new b-a
1 2 -4 -1 1.5 -2.75 c=a=1.5 0.5
1.5 2 -2.75 -1 1.75 -1.9375 c=a=1.75 0.25
1.75 2 -1.9375 -1 1.875 -1.48438 c=a=1.875 0.125
1.875 2 -1.48438 -1 1.9375 -1.2461 c=a=1.9375 0.0625
1.9375 2 -1.2461 -1 1.96875 -1.124 c=a=1.96875 0.03125
1.96875 2 -1.124 -1 1.98438 -1.062 c=a=1.98438 0.01562
1.98438 2 -1.06224 -1 1.99219 -1.03118 c=a=1.99219 0.00781