Introduction to Differential Calculus - PDF

Introduction to differential calculus
Contents
Introduction and background differential calculus......................................................................................2
Specific Objective........................................................................................................................................3
Determination of gradient of curve function f(x) = yn using secant line......................................................4
Determination of differentiation function y = f (x) using chain rule............................................................6
Determination of differentiation function y = f (x) using quotient rule.......................................................8
Solutions to the three questions...............................................................................................................10
Conclusion.................................................................................................................................................14
References.................................................................................................................................................15
1

Introduction and background differential calculus
Today it is by and large trusted that analytics was found freely in the late seventeenth century by
two awesome mathematicians: Isaac Newton and Gottfried Leibniz. In any case, the argument
about who initially found analytics turned into a noteworthy outrage around the turn of the
eighteenth century. Like most logical disclosures, the revelation of analytics did not emerge out
of a vacuum. Truth be told, numerous mathematicians and savants backpedaling to antiquated
circumstances made disclosures identifying with analytics. The antiquated Greeks made
numerous revelations that we would today consider as a feature of math — notwithstanding, for
the most part fundamental analytics, which will be examined in the module Integration. Indian
mathematicians in Kerala had created Taylor polynomials for capacities like sin(x) and cos(x)
before 1500. In the mid seventeenth century, Fermat built up a strategy called adequality for
finding where the subsidiary of a capacity is zero, that is, for understanding f` (x) = 0. Yet, it was
not until Newton and Leibniz that angles of digressions to bends could be figured when all is
said in done.
2

Specific Objective
Having completed this Teaching and Learning Plan the students will be able to:
1. describe rates of change in the real world
2. use mathematical language to describe rates of change
3. use the slope formula to calculate rates of change of linear functions
4. use the slope formula to calculate average rates of change
5. recognize that average rate of change and instantaneous rate of change are identical for
linear functions
6. recognize that average rate of change and instantaneous rate of change are not necessarily
identical for non-linear functions
7. Recognize that the slope of the secant line between two points on a curve is the average
rate of change of the curve between those points
8. To differentiate a function f (x) = x2 using secant line
9. To differentiate a function f (x) = (x7 – x2)42 using chain rule
10. To differentiate a function f(x) = x
√x2 +1 using quotient rule
3

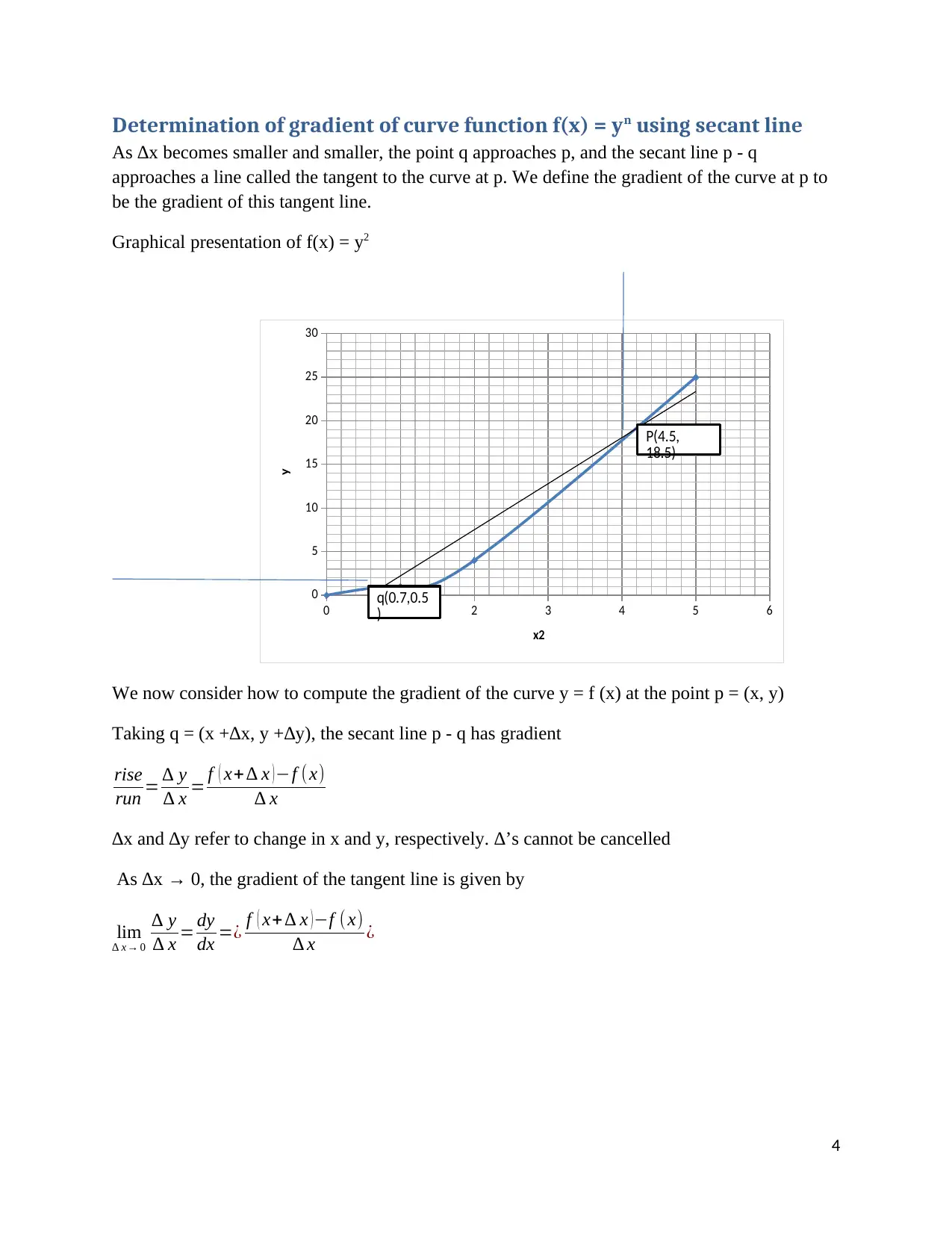
Determination of gradient of curve function f(x) = yn using secant line
As ∆x becomes smaller and smaller, the point q approaches p, and the secant line p - q
approaches a line called the tangent to the curve at p. We define the gradient of the curve at p to
be the gradient of this tangent line.
Graphical presentation of f(x) = y2
0 1 2 3 4 5 6
0
5
10
15
20
25
30
x2
y
P(4.5,
18.5)
q(0.7,0.5
)
We now consider how to compute the gradient of the curve y = f (x) at the point p = (x, y)
Taking q = (x +∆x, y +∆y), the secant line p - q has gradient
rise
run = ∆ y
∆ x = f ( x+∆ x ) −f (x)
∆ x
∆x and ∆y refer to change in x and y, respectively. ∆’s cannot be cancelled
As ∆x → 0, the gradient of the tangent line is given by
lim
∆ x→ 0
∆ y
∆ x = dy
dx =¿ f ( x+∆ x )−f ( x)
∆ x ¿
4

GRADE 12 INTRODUCTIONS TO DIFFERENTIAL CALCULUS
Final practice exam
Name:
Student number:
Attending Non- attending
Phone number:
Address:
Instructions
The final examination will be weighted as follows
Module 1: Derivative of a curve 15 marks
Time: 10 minutes
Note: you are required to bring the following to the exam: pencil(2 or 3 each), blank paper, a
ruler and a scientific calculator.
Show all calculations and formula used. Use all the decimals places in your calculations and
round the final answer to the correct number of decimal places. Include units where appropriate.
Clearly state your final answer.
Module 1
Question 1
Let f (x) = x3. What is the gradient of the tangent line to the graph y = f (x) at the point (2, 8)?
5
For markers use only
Date:
Final mark:
Comments:

Determination of differentiation function y = f (x) using chain rule
The chain rule allows us to differentiate the composition of two functions
Since the composition of two functions g and f is (f ◦ g )(x) = f (g (x)).
We will start with x, apply g , then apply f . The chain rule tells us how to differentiate such a
function.
If we let f , g be differentiable functions. Then the derivative of their composition is
d
dx [ f ( g ( x ) ) ]=¿ f`(g(x))g`(x)
Then the chain rule says that ‘differentials cancel’ in the sense that
dy
dx = dy
du
du
dx
To calculate the derivative, we must evaluate the limit
d
dx [ f ( g ( x ) ) ]=¿ lim
∆ x→ 0
f (g (x+ ∆ x))−f (g(x ))
∆ x
Multiply and divide by an extra term in the expression above, as shown, so that we obtain two
expressions which both express rates of change:
f (g ( x+ ∆ x))−f (g( x ))
∆ x =f ( g( x +∆ x ))−ff ¿ ¿
The ratio in the first limit expresses the change in the function f , from its value at g (x) to its
value at
g (x + ∆x), relative to the difference between g (x + ∆x) and g (x). So as ∆x → 0, this first term
approaches the derivative of f at the point g (x), namely f 0 (g (x)). The second limit is clearly g
0 (x). We conclude that
d
dx [ f ( g ( x ) ) ]=f ( g ( x ) ) g ( x )
6

GRADE 12 INTRODUCTIONS TO DIFFERENTIAL CALCULUS
Final practice exam
Name:
Student number:
Attending Non- attending
Phone number:
Address:
Instructions
The final examination will be weighted as follows
Module 2: Derivative using chain rule 15 marks
Time: 10 minutes
Note: you are required to bring the following to the exam: pencil(2 or 3 each), blank paper, a
ruler and a scientific calculator.
Show all calculations and formula used. Use all the decimals places in your calculations and
round the final answer to the correct number of decimal places. Include units where appropriate.
Clearly state your final answer.
Module 2
Question 2
Let f (x) = (x7 – x2)42. Find the gradient of the value of f(x) that is f`(x) at point (2, 8)
7
For markers use only
Date:
Final mark:
Comments:

Determination of differentiation function y = f (x) using quotient rule
If we let f , g be differentiable functions. Then the derivative of their quotient is
d
dx ( f ( x)
g( x ) ) = g ( x ) f ( x ) −f ( x ) g ( x )
( g ( x ) )2
We can also write
d
dx ( f
g )=
g df
dx −f dg
dx
g2
8

GRADE 12 INTRODUCTIONS TO DIFFERENTIAL CALCULUS
Final practice exam
Name:
Student number:
Attending Non- attending
Phone number:
Address:
Instructions
The final examination will be weighted as follows
Module 1: Derivative using quotient rule 15 marks
Time: 10 minutes
Note: you are required to bring the following to the exam: pencil(2 or 3 each), blank paper, a
ruler and a scientific calculator.
Show all calculations and formula used. Use all the decimals places in your calculations and
round the final answer to the correct number of decimal places. Include units where appropriate.
Clearly state your final answer.
Module 3
Question 3
Let f(x) = x
√x2 +1 , find the gradient of y = f(x) at point (2,8)
9
For markers use only
Date:
Final mark:
Comments:

Solutions to the three questions
GRADE 12 INTRODUCTIONS TO DIFFERENTIAL CALCULUS
Final practice exam
Name:
Student number:
Attending Non- attending
Phone number:
Address:
Instructions
The final examination will be weighted as follows
Module 1: Derivative of a curve 15 marks
Module 2: Derivative using chain rule 15 marks
Module 3: Derivative using quotient rule 15 marks
Time: 30 minutes
Note: you are required to bring the following to the exam: pencil(2 or 3 each), blank paper, a
ruler and a scientific calculator.
Show all calculations and formula used. Use all the decimals places in your calculations and
round the final answer to the correct number of decimal places. Include units where appropriate.
Clearly state your final answer.
10
For markers use only
Date:
Final mark:
Comments:

Module 1
Question 1
Let f (x) = x3. What is the gradient of the tangent line to the graph y = f (x) at the point (2, 8)?
Solution
The gradient at x = 2 is given by the limit
lim
∆ x→ 0
f (2+ ∆ x)−f (2)
∆ x
= lim
∆ x→ 0
f ( 2+ ∆ x )3−f ( 2 )2
∆ x
= lim
∆ x→ 0
8+12(∆ x )+6 ( ∆ x )2 + ( ∆ x )3−8
∆ x
= lim
∆ x→ 0
12+6 ( ∆ x ) + ( ∆ x ) 2
=12
Thus the gradient of the tangent line to y = f (x) at (2, 8) is 12.
11

Module 2
Question 2
Let f (x) = (x7 – x2)42. Find the gradient of the value of f(x) that is f`(x) at point (2, 8)
Solution
Let u = x7 – x2
So that y = u42
We have
dy
dx =¿ 42u41
du
dx =¿7x6 – 2x
And the chain rule gives
dy
dx =
dy
dx ∗du
dx
= 42u41(7x6 – 2x)
Rewriting u in terms of x
dy
dx = 42(x7 – x2)41(7x6-2x)
At x = 2, we substitute the value of 2 in x
= 42(27 – 22)41(7*26 – 2*2)
= 1.2616 * 1090
12

Module 3
Question 3
Let f(x) = x
√x2 +1 , find the gradient of y = f(x) at point (2,8)
Solution
We apply the quotient rule
f`(x) = √x2 +1 d
dx ( x )−x d
dx √x2 +1
x2 +1
to differentiate √ x2+1, we use chain rule
d
dx ( x2+ 1 )
1
2 = 1
2 ( x2+ 1 )
−1
2 d
dx (x2 +1)
= 1
2 ( x2+1 )
−1
2 (2 x )
= x(x2 + 1)-1/2
Now returning to f`(x) we obtain
f`(x) = √x2 +1∗1−x∗x ( x2 +1 )
−1
2
x2 +1
=
( x2+1 ) −x2
( x2+1 )
3
2
= (x2 + 1)-3/2
Substituting the value of x at x = 2
(22 + 1)-3/2
13

=
1
( 22+1 )
3
2
= 0.08944
Conclusion
We can summarize the differentiation rules we have found as follows.
Linearity differentiation
f ( x+∆ x ) −f ( x)
∆ x
Quotient and chain rules
Chain rule
d
dx [ f ( g ( x ) ) ]=f ( g ( x ) ) g ( x )
Quotient rule
d
dx ( f
g )=
g df
dx −f dg
dx
g2
14

References
David Bressoud. (2002). Was calculus invented in India?. College Mathematics Journal 33.
Alfred Rupert Hall. (1980). Philosophers at War: The Quarrel between Newton and Leibniz. Cambridge
University Press.
15