Investment Management: Bond Portfolio Strategy and Yield Analysis
VerifiedAdded on 2023/06/11
|14
|1715
|249
Homework Assignment
AI Summary
This assignment focuses on investment management principles, specifically addressing bond portfolio hedging, yield curve analysis, and yield to maturity (YTM) calculations. It begins by calculating bond prices and depicting the yield curve, followed by determining the YTM for various maturities. The assignment then constructs an arbitrage portfolio and examines the relationship between Holding Period Return (HPR) and changes in YTM, including scenarios involving short selling. Further analysis explores the impact of coupon rate changes on HPR. Finally, the assignment delves into cash flow matching, calculating the present value of liabilities and determining portfolio weights to immunize against interest rate risk, including scenarios where the yield curve shifts. The study uses hedging measures to minimize investment risk and maximize profitability.

Running head: INVESTMENT MANAGEMENT
Investment Management
Name of the Student:
Name of the University:
Authors Note:
Investment Management
Name of the Student:
Name of the University:
Authors Note:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

INVESTMENT MANAGEMENT
1
Table of Contents
Question 1:.................................................................................................................................2
a. Calculating bond prices and depicting yield curve:...............................................................2
b. Calculating Yield to maturity:................................................................................................3
c. Constructing arbitrage portfolio:............................................................................................5
Question 2:.................................................................................................................................5
a. Relationship between HPR and changes in the YTM:...........................................................5
b. Repeating the process with short sell:....................................................................................7
c. Relationship between HPR and changes in the Coupon rate:................................................8
Question 3:...............................................................................................................................10
a. Using present yield curve for detecting present value of the liability:.................................10
b. Calculating weights of the portfolio:....................................................................................10
c. Calculating PV of the liability and weights of the portfolio if yield curve shifts down size
by 100 basis points:..................................................................................................................11
References:...............................................................................................................................13
1
Table of Contents
Question 1:.................................................................................................................................2
a. Calculating bond prices and depicting yield curve:...............................................................2
b. Calculating Yield to maturity:................................................................................................3
c. Constructing arbitrage portfolio:............................................................................................5
Question 2:.................................................................................................................................5
a. Relationship between HPR and changes in the YTM:...........................................................5
b. Repeating the process with short sell:....................................................................................7
c. Relationship between HPR and changes in the Coupon rate:................................................8
Question 3:...............................................................................................................................10
a. Using present yield curve for detecting present value of the liability:.................................10
b. Calculating weights of the portfolio:....................................................................................10
c. Calculating PV of the liability and weights of the portfolio if yield curve shifts down size
by 100 basis points:..................................................................................................................11
References:...............................................................................................................................13
INVESTMENT MANAGEMENT
2
Question 1:
a. Calculating bond prices and depicting yield curve:
Maturity (years) Market Price of Bond
0.50 100.69
1.00 103.34
1.50 100.80
2.00 102.47
2.50 99.67
3.00 103.55
3.50 103.43
4.00 103.08
4.50 100.25
5.00 100.65
5.50 101.56
6.00 102.00
6.50 100.00
7.00 99.50
7.50 100.47
8.00 101.54
8.50 99.74
9.00 100.68
9.50 100.13
10.00 99.76
2
Question 1:
a. Calculating bond prices and depicting yield curve:
Maturity (years) Market Price of Bond
0.50 100.69
1.00 103.34
1.50 100.80
2.00 102.47
2.50 99.67
3.00 103.55
3.50 103.43
4.00 103.08
4.50 100.25
5.00 100.65
5.50 101.56
6.00 102.00
6.50 100.00
7.00 99.50
7.50 100.47
8.00 101.54
8.50 99.74
9.00 100.68
9.50 100.13
10.00 99.76
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
INVESTMENT MANAGEMENT
3
0.00 2.00 4.00 6.00 8.00 10.00 12.00
0.000%
0.500%
1.000%
1.500%
2.000%
2.500%
3.000%
3.500%
Yeild Curve
Zero-Coupon Yields
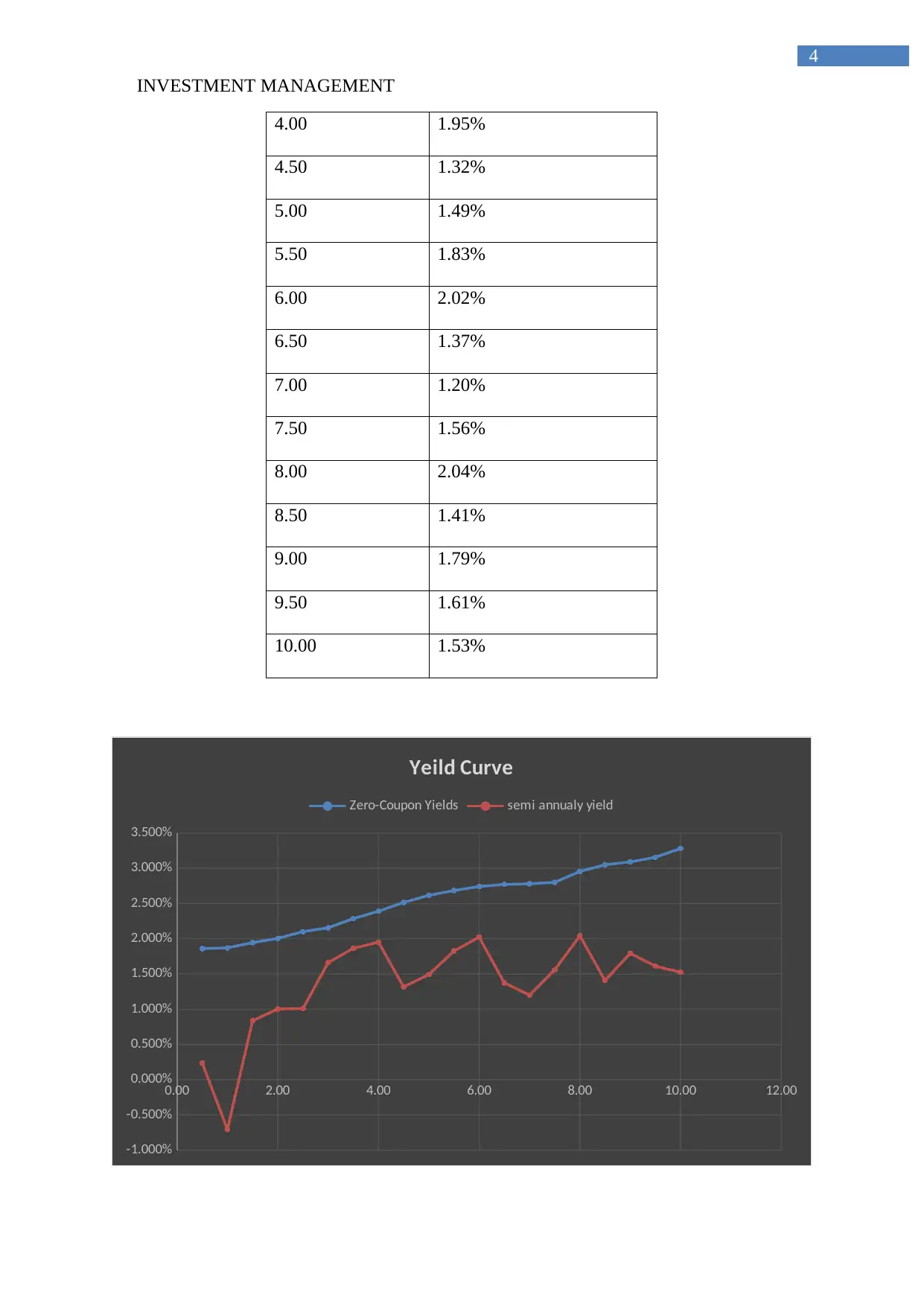
The general shape of the yield is approximately, as the above figure. However, the
curve is mainly smooth and tends to increase with tenure and decline after some years. The
change in bond prices and income tends to alter the YTM of the bond investment.
b. Calculating Yield to maturity:
Maturity (years) Semi-annually yield
0.50 0.24%
1.00 -0.71%
1.50 0.84%
2.00 1.00%
2.50 1.01%
3.00 1.66%
3.50 1.86%
3
0.00 2.00 4.00 6.00 8.00 10.00 12.00
0.000%
0.500%
1.000%
1.500%
2.000%
2.500%
3.000%
3.500%
Yeild Curve
Zero-Coupon Yields
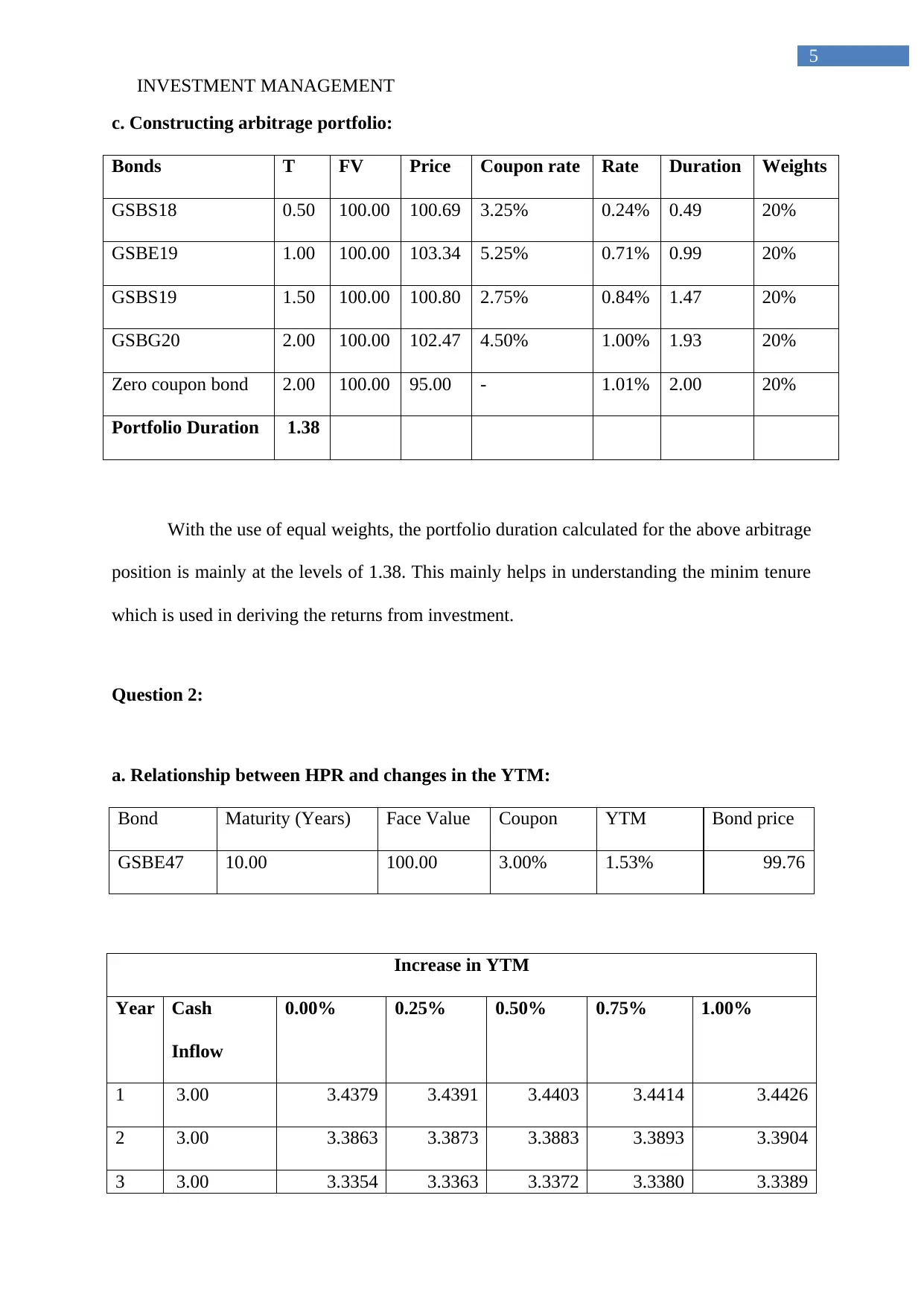
The general shape of the yield is approximately, as the above figure. However, the
curve is mainly smooth and tends to increase with tenure and decline after some years. The
change in bond prices and income tends to alter the YTM of the bond investment.
b. Calculating Yield to maturity:
Maturity (years) Semi-annually yield
0.50 0.24%
1.00 -0.71%
1.50 0.84%
2.00 1.00%
2.50 1.01%
3.00 1.66%
3.50 1.86%
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
INVESTMENT MANAGEMENT
4
4.00 1.95%
4.50 1.32%
5.00 1.49%
5.50 1.83%
6.00 2.02%
6.50 1.37%
7.00 1.20%
7.50 1.56%
8.00 2.04%
8.50 1.41%
9.00 1.79%
9.50 1.61%
10.00 1.53%
0.00 2.00 4.00 6.00 8.00 10.00 12.00
-1.000%
-0.500%
0.000%
0.500%
1.000%
1.500%
2.000%
2.500%
3.000%
3.500%
Yeild Curve
Zero-Coupon Yields semi annualy yield
4
4.00 1.95%
4.50 1.32%
5.00 1.49%
5.50 1.83%
6.00 2.02%
6.50 1.37%
7.00 1.20%
7.50 1.56%
8.00 2.04%
8.50 1.41%
9.00 1.79%
9.50 1.61%
10.00 1.53%
0.00 2.00 4.00 6.00 8.00 10.00 12.00
-1.000%
-0.500%
0.000%
0.500%
1.000%
1.500%
2.000%
2.500%
3.000%
3.500%
Yeild Curve
Zero-Coupon Yields semi annualy yield
INVESTMENT MANAGEMENT
5
c. Constructing arbitrage portfolio:
Bonds T FV Price Coupon rate Rate Duration Weights
GSBS18 0.50 100.00 100.69 3.25% 0.24% 0.49 20%
GSBE19 1.00 100.00 103.34 5.25% 0.71% 0.99 20%
GSBS19 1.50 100.00 100.80 2.75% 0.84% 1.47 20%
GSBG20 2.00 100.00 102.47 4.50% 1.00% 1.93 20%
Zero coupon bond 2.00 100.00 95.00 - 1.01% 2.00 20%
Portfolio Duration 1.38
With the use of equal weights, the portfolio duration calculated for the above arbitrage
position is mainly at the levels of 1.38. This mainly helps in understanding the minim tenure
which is used in deriving the returns from investment.
Question 2:
a. Relationship between HPR and changes in the YTM:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 3.00% 1.53% 99.76
Increase in YTM
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4391 3.4403 3.4414 3.4426
2 3.00 3.3863 3.3873 3.3883 3.3893 3.3904
3 3.00 3.3354 3.3363 3.3372 3.3380 3.3389
5
c. Constructing arbitrage portfolio:
Bonds T FV Price Coupon rate Rate Duration Weights
GSBS18 0.50 100.00 100.69 3.25% 0.24% 0.49 20%
GSBE19 1.00 100.00 103.34 5.25% 0.71% 0.99 20%
GSBS19 1.50 100.00 100.80 2.75% 0.84% 1.47 20%
GSBG20 2.00 100.00 102.47 4.50% 1.00% 1.93 20%
Zero coupon bond 2.00 100.00 95.00 - 1.01% 2.00 20%
Portfolio Duration 1.38
With the use of equal weights, the portfolio duration calculated for the above arbitrage
position is mainly at the levels of 1.38. This mainly helps in understanding the minim tenure
which is used in deriving the returns from investment.
Question 2:
a. Relationship between HPR and changes in the YTM:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 3.00% 1.53% 99.76
Increase in YTM
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4391 3.4403 3.4414 3.4426
2 3.00 3.3863 3.3873 3.3883 3.3893 3.3904
3 3.00 3.3354 3.3363 3.3372 3.3380 3.3389
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
INVESTMENT MANAGEMENT
6
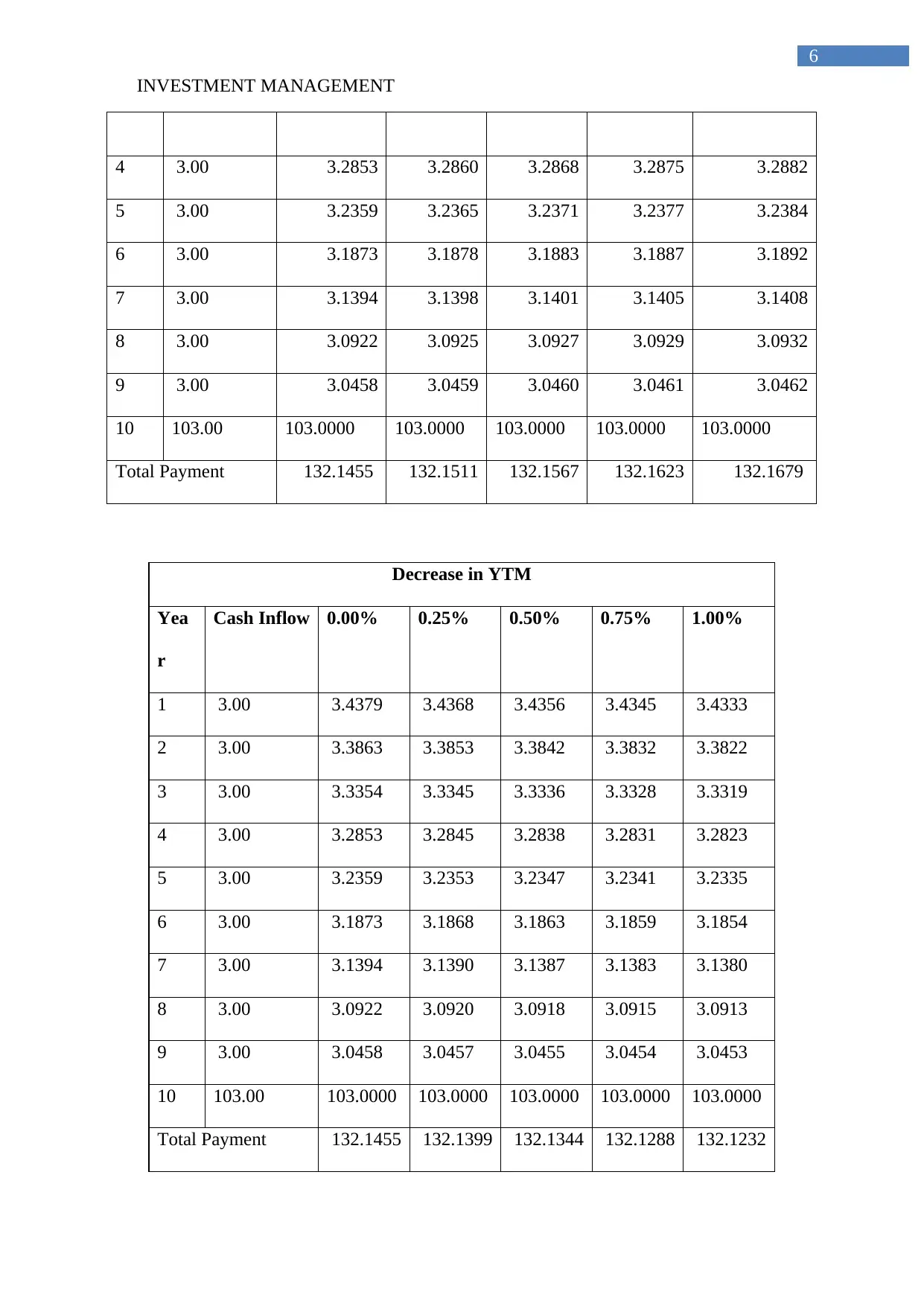
4 3.00 3.2853 3.2860 3.2868 3.2875 3.2882
5 3.00 3.2359 3.2365 3.2371 3.2377 3.2384
6 3.00 3.1873 3.1878 3.1883 3.1887 3.1892
7 3.00 3.1394 3.1398 3.1401 3.1405 3.1408
8 3.00 3.0922 3.0925 3.0927 3.0929 3.0932
9 3.00 3.0458 3.0459 3.0460 3.0461 3.0462
10 103.00 103.0000 103.0000 103.0000 103.0000 103.0000
Total Payment 132.1455 132.1511 132.1567 132.1623 132.1679
Decrease in YTM
Yea
r
Cash Inflow 0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4368 3.4356 3.4345 3.4333
2 3.00 3.3863 3.3853 3.3842 3.3832 3.3822
3 3.00 3.3354 3.3345 3.3336 3.3328 3.3319
4 3.00 3.2853 3.2845 3.2838 3.2831 3.2823
5 3.00 3.2359 3.2353 3.2347 3.2341 3.2335
6 3.00 3.1873 3.1868 3.1863 3.1859 3.1854
7 3.00 3.1394 3.1390 3.1387 3.1383 3.1380
8 3.00 3.0922 3.0920 3.0918 3.0915 3.0913
9 3.00 3.0458 3.0457 3.0455 3.0454 3.0453
10 103.00 103.0000 103.0000 103.0000 103.0000 103.0000
Total Payment 132.1455 132.1399 132.1344 132.1288 132.1232
6
4 3.00 3.2853 3.2860 3.2868 3.2875 3.2882
5 3.00 3.2359 3.2365 3.2371 3.2377 3.2384
6 3.00 3.1873 3.1878 3.1883 3.1887 3.1892
7 3.00 3.1394 3.1398 3.1401 3.1405 3.1408
8 3.00 3.0922 3.0925 3.0927 3.0929 3.0932
9 3.00 3.0458 3.0459 3.0460 3.0461 3.0462
10 103.00 103.0000 103.0000 103.0000 103.0000 103.0000
Total Payment 132.1455 132.1511 132.1567 132.1623 132.1679
Decrease in YTM
Yea
r
Cash Inflow 0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4368 3.4356 3.4345 3.4333
2 3.00 3.3863 3.3853 3.3842 3.3832 3.3822
3 3.00 3.3354 3.3345 3.3336 3.3328 3.3319
4 3.00 3.2853 3.2845 3.2838 3.2831 3.2823
5 3.00 3.2359 3.2353 3.2347 3.2341 3.2335
6 3.00 3.1873 3.1868 3.1863 3.1859 3.1854
7 3.00 3.1394 3.1390 3.1387 3.1383 3.1380
8 3.00 3.0922 3.0920 3.0918 3.0915 3.0913
9 3.00 3.0458 3.0457 3.0455 3.0454 3.0453
10 103.00 103.0000 103.0000 103.0000 103.0000 103.0000
Total Payment 132.1455 132.1399 132.1344 132.1288 132.1232
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
INVESTMENT MANAGEMENT
7
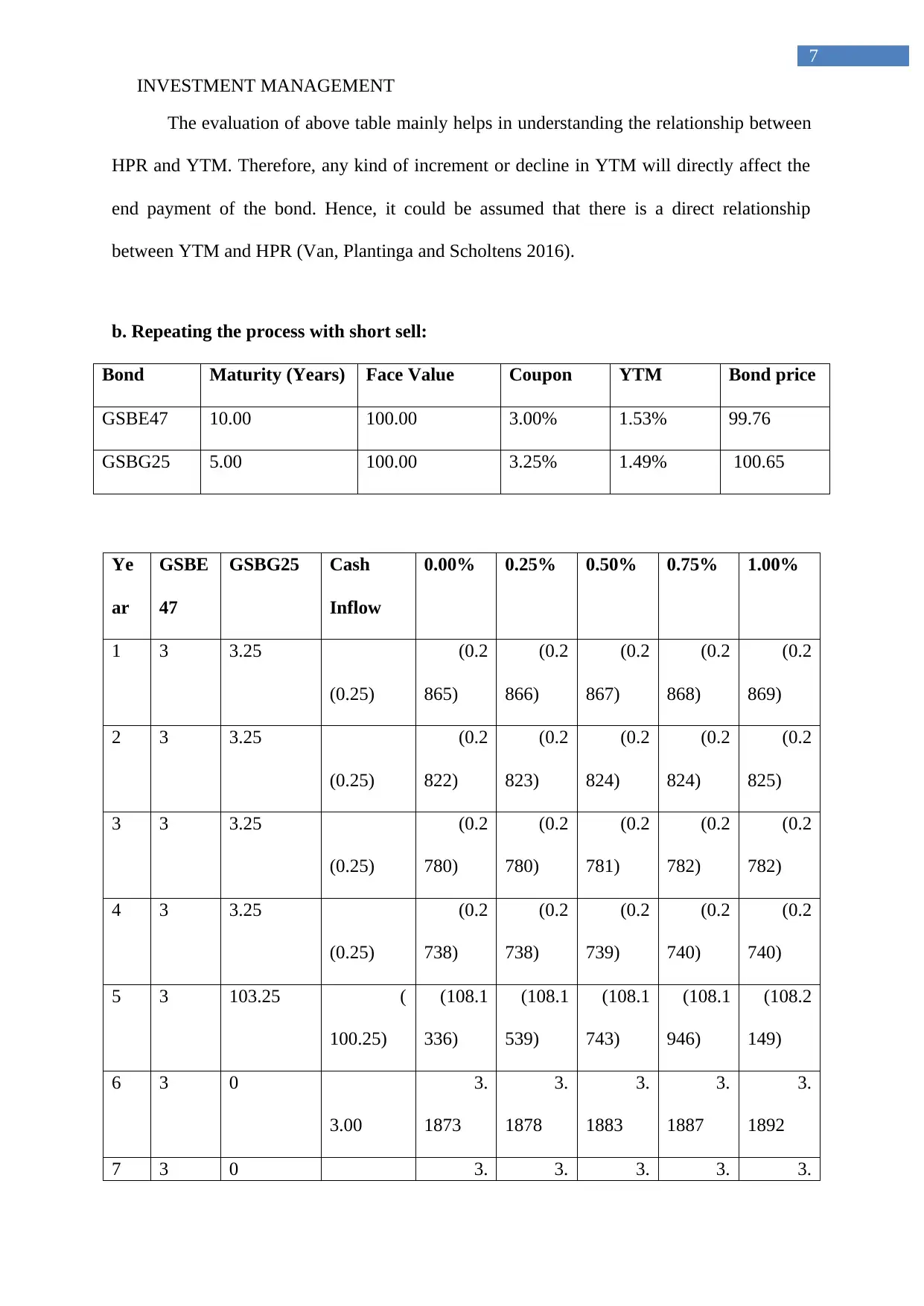
The evaluation of above table mainly helps in understanding the relationship between
HPR and YTM. Therefore, any kind of increment or decline in YTM will directly affect the
end payment of the bond. Hence, it could be assumed that there is a direct relationship
between YTM and HPR (Van, Plantinga and Scholtens 2016).
b. Repeating the process with short sell:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 3.00% 1.53% 99.76
GSBG25 5.00 100.00 3.25% 1.49% 100.65
Ye
ar
GSBE
47
GSBG25 Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3 3.25
(0.25)
(0.2
865)
(0.2
866)
(0.2
867)
(0.2
868)
(0.2
869)
2 3 3.25
(0.25)
(0.2
822)
(0.2
823)
(0.2
824)
(0.2
824)
(0.2
825)
3 3 3.25
(0.25)
(0.2
780)
(0.2
780)
(0.2
781)
(0.2
782)
(0.2
782)
4 3 3.25
(0.25)
(0.2
738)
(0.2
738)
(0.2
739)
(0.2
740)
(0.2
740)
5 3 103.25 (
100.25)
(108.1
336)
(108.1
539)
(108.1
743)
(108.1
946)
(108.2
149)
6 3 0
3.00
3.
1873
3.
1878
3.
1883
3.
1887
3.
1892
7 3 0 3. 3. 3. 3. 3.
7
The evaluation of above table mainly helps in understanding the relationship between
HPR and YTM. Therefore, any kind of increment or decline in YTM will directly affect the
end payment of the bond. Hence, it could be assumed that there is a direct relationship
between YTM and HPR (Van, Plantinga and Scholtens 2016).
b. Repeating the process with short sell:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 3.00% 1.53% 99.76
GSBG25 5.00 100.00 3.25% 1.49% 100.65
Ye
ar
GSBE
47
GSBG25 Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3 3.25
(0.25)
(0.2
865)
(0.2
866)
(0.2
867)
(0.2
868)
(0.2
869)
2 3 3.25
(0.25)
(0.2
822)
(0.2
823)
(0.2
824)
(0.2
824)
(0.2
825)
3 3 3.25
(0.25)
(0.2
780)
(0.2
780)
(0.2
781)
(0.2
782)
(0.2
782)
4 3 3.25
(0.25)
(0.2
738)
(0.2
738)
(0.2
739)
(0.2
740)
(0.2
740)
5 3 103.25 (
100.25)
(108.1
336)
(108.1
539)
(108.1
743)
(108.1
946)
(108.2
149)
6 3 0
3.00
3.
1873
3.
1878
3.
1883
3.
1887
3.
1892
7 3 0 3. 3. 3. 3. 3.
INVESTMENT MANAGEMENT
8
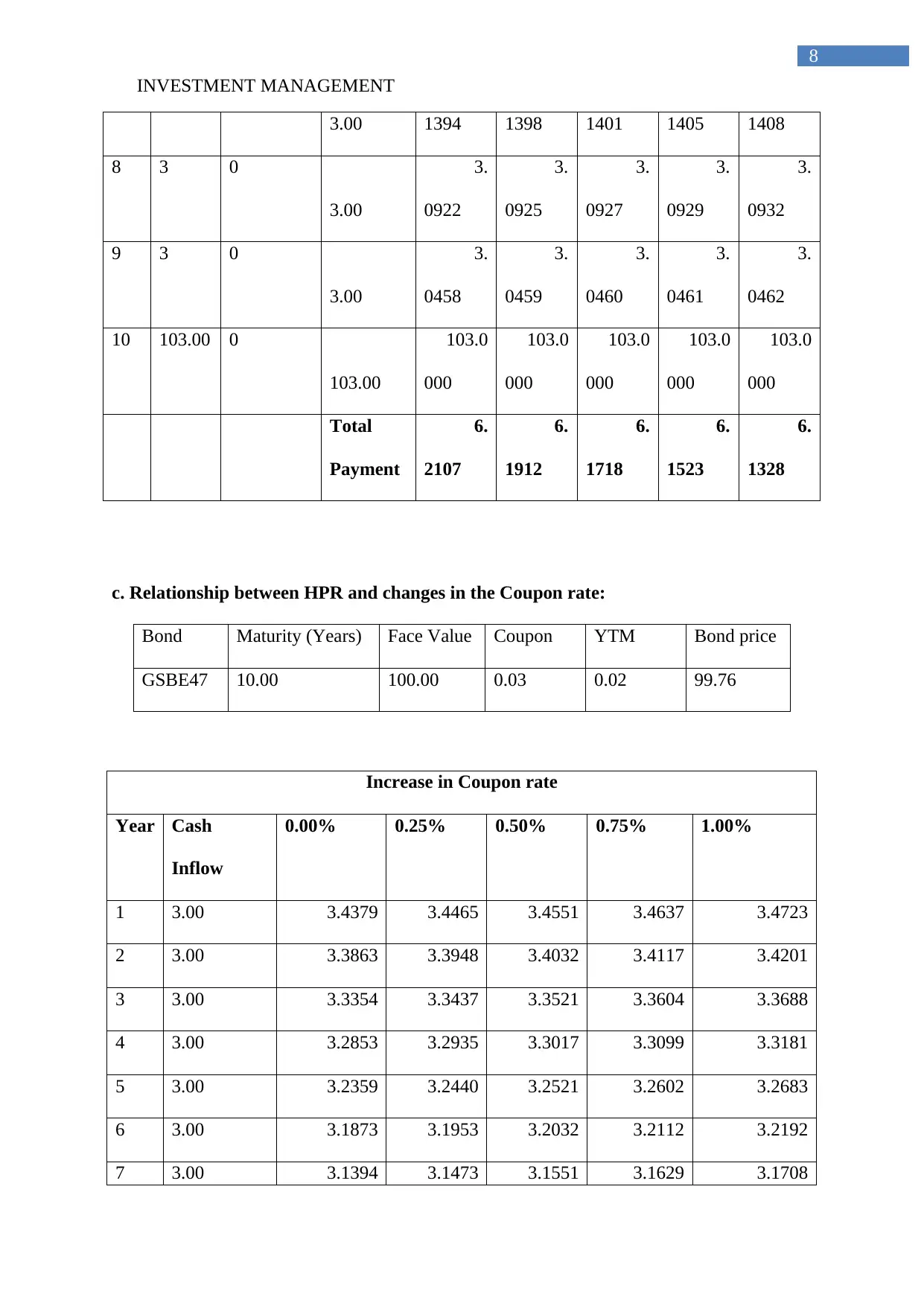
3.00 1394 1398 1401 1405 1408
8 3 0
3.00
3.
0922
3.
0925
3.
0927
3.
0929
3.
0932
9 3 0
3.00
3.
0458
3.
0459
3.
0460
3.
0461
3.
0462
10 103.00 0
103.00
103.0
000
103.0
000
103.0
000
103.0
000
103.0
000
Total
Payment
6.
2107
6.
1912
6.
1718
6.
1523
6.
1328
c. Relationship between HPR and changes in the Coupon rate:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 0.03 0.02 99.76
Increase in Coupon rate
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4465 3.4551 3.4637 3.4723
2 3.00 3.3863 3.3948 3.4032 3.4117 3.4201
3 3.00 3.3354 3.3437 3.3521 3.3604 3.3688
4 3.00 3.2853 3.2935 3.3017 3.3099 3.3181
5 3.00 3.2359 3.2440 3.2521 3.2602 3.2683
6 3.00 3.1873 3.1953 3.2032 3.2112 3.2192
7 3.00 3.1394 3.1473 3.1551 3.1629 3.1708
8
3.00 1394 1398 1401 1405 1408
8 3 0
3.00
3.
0922
3.
0925
3.
0927
3.
0929
3.
0932
9 3 0
3.00
3.
0458
3.
0459
3.
0460
3.
0461
3.
0462
10 103.00 0
103.00
103.0
000
103.0
000
103.0
000
103.0
000
103.0
000
Total
Payment
6.
2107
6.
1912
6.
1718
6.
1523
6.
1328
c. Relationship between HPR and changes in the Coupon rate:
Bond Maturity (Years) Face Value Coupon YTM Bond price
GSBE47 10.00 100.00 0.03 0.02 99.76
Increase in Coupon rate
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4465 3.4551 3.4637 3.4723
2 3.00 3.3863 3.3948 3.4032 3.4117 3.4201
3 3.00 3.3354 3.3437 3.3521 3.3604 3.3688
4 3.00 3.2853 3.2935 3.3017 3.3099 3.3181
5 3.00 3.2359 3.2440 3.2521 3.2602 3.2683
6 3.00 3.1873 3.1953 3.2032 3.2112 3.2192
7 3.00 3.1394 3.1473 3.1551 3.1629 3.1708
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
INVESTMENT MANAGEMENT
9
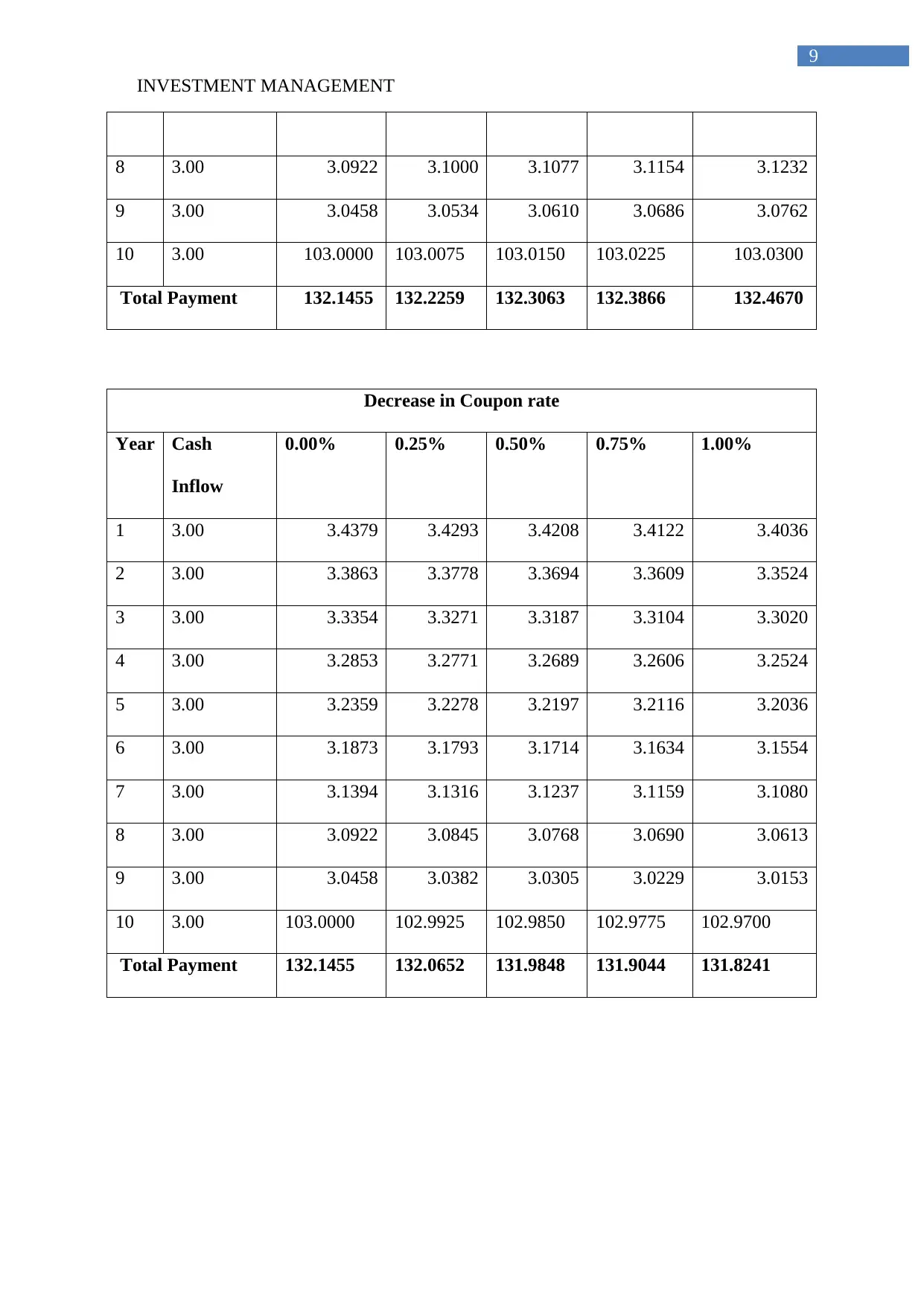
8 3.00 3.0922 3.1000 3.1077 3.1154 3.1232
9 3.00 3.0458 3.0534 3.0610 3.0686 3.0762
10 3.00 103.0000 103.0075 103.0150 103.0225 103.0300
Total Payment 132.1455 132.2259 132.3063 132.3866 132.4670
Decrease in Coupon rate
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4293 3.4208 3.4122 3.4036
2 3.00 3.3863 3.3778 3.3694 3.3609 3.3524
3 3.00 3.3354 3.3271 3.3187 3.3104 3.3020
4 3.00 3.2853 3.2771 3.2689 3.2606 3.2524
5 3.00 3.2359 3.2278 3.2197 3.2116 3.2036
6 3.00 3.1873 3.1793 3.1714 3.1634 3.1554
7 3.00 3.1394 3.1316 3.1237 3.1159 3.1080
8 3.00 3.0922 3.0845 3.0768 3.0690 3.0613
9 3.00 3.0458 3.0382 3.0305 3.0229 3.0153
10 3.00 103.0000 102.9925 102.9850 102.9775 102.9700
Total Payment 132.1455 132.0652 131.9848 131.9044 131.8241
9
8 3.00 3.0922 3.1000 3.1077 3.1154 3.1232
9 3.00 3.0458 3.0534 3.0610 3.0686 3.0762
10 3.00 103.0000 103.0075 103.0150 103.0225 103.0300
Total Payment 132.1455 132.2259 132.3063 132.3866 132.4670
Decrease in Coupon rate
Year Cash
Inflow
0.00% 0.25% 0.50% 0.75% 1.00%
1 3.00 3.4379 3.4293 3.4208 3.4122 3.4036
2 3.00 3.3863 3.3778 3.3694 3.3609 3.3524
3 3.00 3.3354 3.3271 3.3187 3.3104 3.3020
4 3.00 3.2853 3.2771 3.2689 3.2606 3.2524
5 3.00 3.2359 3.2278 3.2197 3.2116 3.2036
6 3.00 3.1873 3.1793 3.1714 3.1634 3.1554
7 3.00 3.1394 3.1316 3.1237 3.1159 3.1080
8 3.00 3.0922 3.0845 3.0768 3.0690 3.0613
9 3.00 3.0458 3.0382 3.0305 3.0229 3.0153
10 3.00 103.0000 102.9925 102.9850 102.9775 102.9700
Total Payment 132.1455 132.0652 131.9848 131.9044 131.8241
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

INVESTMENT MANAGEMENT
10
Question 3:
a. Using present yield curve for detecting present value of the liability:
Liability
F(L) 100,000,000
t 1
Yield 2.62%
PV(L) 97,451,639.62
b. Calculating weights of the portfolio:
Bond 1
F 100
c 2.75%
t 4.50
C 1.375
P
1
90.65
Bond 2
F 100
c 3.25%
t 5.00
C 1.625
P1 100.49
10
Question 3:
a. Using present yield curve for detecting present value of the liability:
Liability
F(L) 100,000,000
t 1
Yield 2.62%
PV(L) 97,451,639.62
b. Calculating weights of the portfolio:
Bond 1
F 100
c 2.75%
t 4.50
C 1.375
P
1
90.65
Bond 2
F 100
c 3.25%
t 5.00
C 1.625
P1 100.49
INVESTMENT MANAGEMENT
11
Cash Flow
Time (year) B1 B2 L checking
4.50 101.375 1.625 0 0
5.00 0 101.625 100,000,000 100,000,000
Bond Portfolio No of bond bond price $ invest
B1 -15773.27734 90.65410927 -1429912.407
B2 984009.8401 100.4883773 98881552.03
B 97451639.62 97451639.62
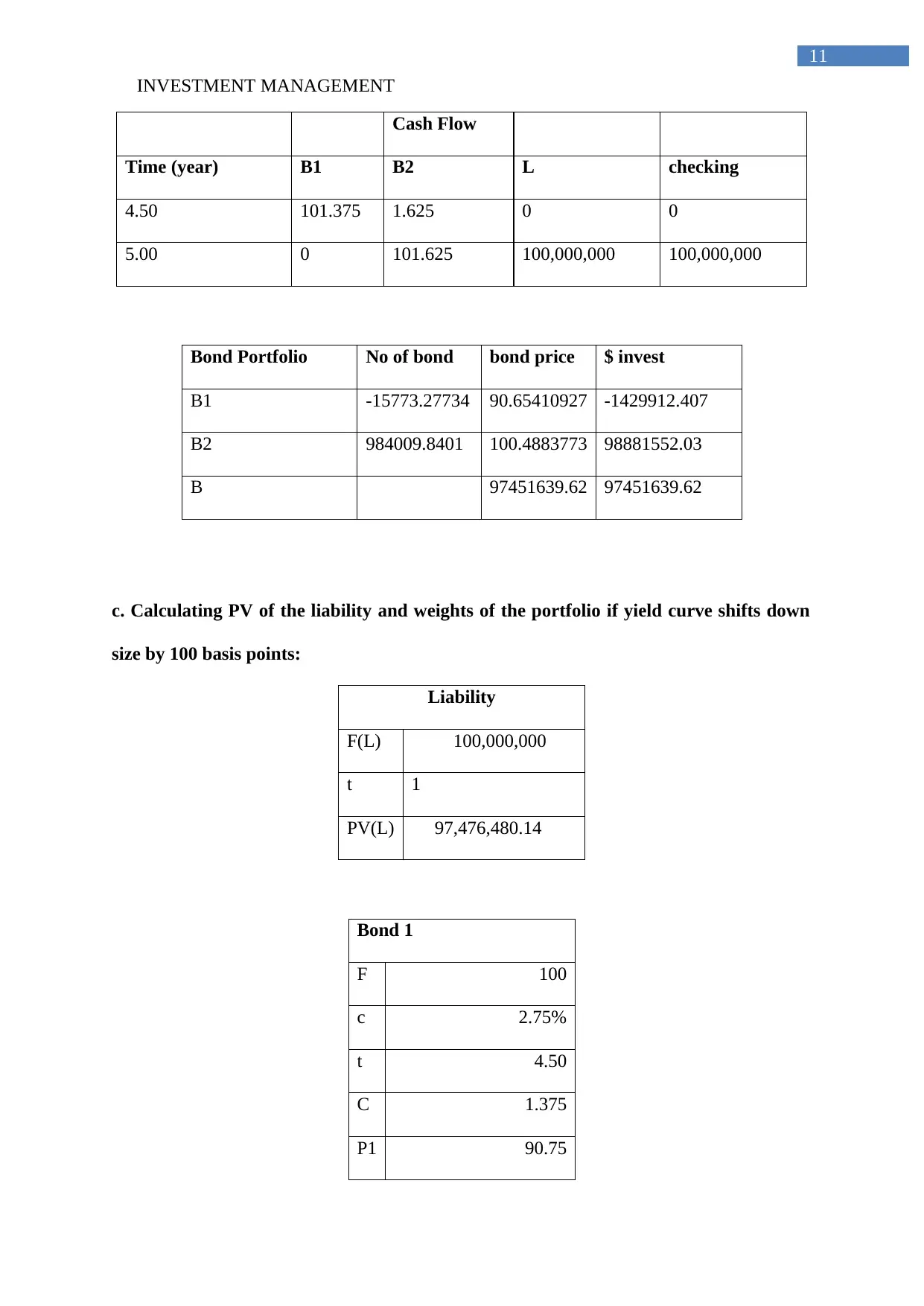
c. Calculating PV of the liability and weights of the portfolio if yield curve shifts down
size by 100 basis points:
Liability
F(L) 100,000,000
t 1
PV(L) 97,476,480.14
Bond 1
F 100
c 2.75%
t 4.50
C 1.375
P1 90.75
11
Cash Flow
Time (year) B1 B2 L checking
4.50 101.375 1.625 0 0
5.00 0 101.625 100,000,000 100,000,000
Bond Portfolio No of bond bond price $ invest
B1 -15773.27734 90.65410927 -1429912.407
B2 984009.8401 100.4883773 98881552.03
B 97451639.62 97451639.62
c. Calculating PV of the liability and weights of the portfolio if yield curve shifts down
size by 100 basis points:
Liability
F(L) 100,000,000
t 1
PV(L) 97,476,480.14
Bond 1
F 100
c 2.75%
t 4.50
C 1.375
P1 90.75
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 14
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




