Bond Pricing and Valuation
VerifiedAdded on 2020/03/16
|8
|1838
|229
AI Summary
This assignment delves into the concepts of bond pricing and stock valuation. It begins by analyzing how changes in interest rates affect bond prices, highlighting the role of interest rate elasticity. Subsequently, it applies the Dividend Discount Model to determine the value of a share based on expected dividends and growth rates. The assignment further explores the impact of varying growth rates on stock prices using a case study with specific dividend payments and return expectations.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Investments and Portfolio Management
[Type the abstract of the document here. The abstract is typically a short summary of the contents
of the document. Type the abstract of the document here. The abstract is typically a short
summary of the contents of the document.]
[Type the abstract of the document here. The abstract is typically a short summary of the contents
of the document. Type the abstract of the document here. The abstract is typically a short
summary of the contents of the document.]
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Question 1
a) Benchmark index is a group of stocks/securities which are used as benchmarks to compare
the performance of stocks. These are also called the market index. The benchmark index for
certain countries is given below:
Country Benchmark Index
Australia ASX 200
USA Dow Jones
Hong Kong Hang Seng
Japan Nikkei Index
England FTSE 100
China Shanghai
(Economics, 2017)
b) There are various types of mutual funds options available to an investor. Each mutual fund
has its own differential features and advantages. The asset classes and the allocation of
different assets for three mutual funds i.e. stable fund, balance fund and growth fund are
discussed below:
i) Stable – A stable fund is a fund for retirement plans. Under this fund, the main investment
asset is wrapped bonds which is the guaranteed investment certificate (GICs), these GICs are
paired with insurance policies to give a minimum yield on the principal amount invested and
also to preserve the principal amount. The bonds of the fund can be short term and
intermediate term.
ii) Balance fund – A balance fund comprises of three asset classes which are stock, bond and
money market. The differential feature of balance fund is that the mix of stocks and bonds
does not change and remains constant as the minimum and maximum amount invested in
each asset class is fixed. The fund can have higher equity component making the fund
moderate or a higher bond component making the fund conservative. Balance fund is
preferred by investors who are looking for safety, income and a modest capital appreciation.
iii) Growth fund – A growth fund comprises of only stocks. The fund consists of a portfolio
of diversified stocks. The primary goal of the fund is capital appreciation. The fund
a) Benchmark index is a group of stocks/securities which are used as benchmarks to compare
the performance of stocks. These are also called the market index. The benchmark index for
certain countries is given below:
Country Benchmark Index
Australia ASX 200
USA Dow Jones
Hong Kong Hang Seng
Japan Nikkei Index
England FTSE 100
China Shanghai
(Economics, 2017)
b) There are various types of mutual funds options available to an investor. Each mutual fund
has its own differential features and advantages. The asset classes and the allocation of
different assets for three mutual funds i.e. stable fund, balance fund and growth fund are
discussed below:
i) Stable – A stable fund is a fund for retirement plans. Under this fund, the main investment
asset is wrapped bonds which is the guaranteed investment certificate (GICs), these GICs are
paired with insurance policies to give a minimum yield on the principal amount invested and
also to preserve the principal amount. The bonds of the fund can be short term and
intermediate term.
ii) Balance fund – A balance fund comprises of three asset classes which are stock, bond and
money market. The differential feature of balance fund is that the mix of stocks and bonds
does not change and remains constant as the minimum and maximum amount invested in
each asset class is fixed. The fund can have higher equity component making the fund
moderate or a higher bond component making the fund conservative. Balance fund is
preferred by investors who are looking for safety, income and a modest capital appreciation.
iii) Growth fund – A growth fund comprises of only stocks. The fund consists of a portfolio
of diversified stocks. The primary goal of the fund is capital appreciation. The fund

comprises of stocks of companies which have above average growth and these companies
mostly reinvest their earning for expansion and acquisitions. Growth funds can be large cap,
mid cap and small cap.
Question 2
Interest elasticity is the sensitivity of the price of the fixed income securities to the interest
rates. Higher interest elasticity means that with a small change in the interest rates, the prices
of securities fluctuate by a higher amount. Duration of a fixed income security measures the
average life of a bond. Duration provides an estimate of the sensitivity of the bond prices to
the interest rates. Higher the duration, higher is the sensitivity of the interest rates to the bond
prices and vice versa (Bodie, Kane, & Marcus, 2016). Like if the interest rate increases by
1%, and the duration of a bond is 5 years, the prices of bond will decline by 5%.
Prices and duration of a bond or fixed income security are related from the point of view of
interest rates. Price and interest rates have an inverse relationship. The sensitivity of price and
interest rate is measured by duration. Duration determines the change in price as a result of a
change in interest rate.
Question 3
Face value (F) = $1000
Market price (P) = $1000
Coupon rate (C) = 10% paid semi annually
Maturity (n) = 11 years
a) Duration of the Treasury bond = present value of cash flows weighted by the length of
time to receiving the cash and divided by the current selling price of the bond.
For discounting the cash flows, the yield to maturity needs to be calculated to be used as
discount rate.
Yield to maturity = [(C+ (F-P))/n] / [F+P]/2
= [50 + (0/22)] / [2000/2]
mostly reinvest their earning for expansion and acquisitions. Growth funds can be large cap,
mid cap and small cap.
Question 2
Interest elasticity is the sensitivity of the price of the fixed income securities to the interest
rates. Higher interest elasticity means that with a small change in the interest rates, the prices
of securities fluctuate by a higher amount. Duration of a fixed income security measures the
average life of a bond. Duration provides an estimate of the sensitivity of the bond prices to
the interest rates. Higher the duration, higher is the sensitivity of the interest rates to the bond
prices and vice versa (Bodie, Kane, & Marcus, 2016). Like if the interest rate increases by
1%, and the duration of a bond is 5 years, the prices of bond will decline by 5%.
Prices and duration of a bond or fixed income security are related from the point of view of
interest rates. Price and interest rates have an inverse relationship. The sensitivity of price and
interest rate is measured by duration. Duration determines the change in price as a result of a
change in interest rate.
Question 3
Face value (F) = $1000
Market price (P) = $1000
Coupon rate (C) = 10% paid semi annually
Maturity (n) = 11 years
a) Duration of the Treasury bond = present value of cash flows weighted by the length of
time to receiving the cash and divided by the current selling price of the bond.
For discounting the cash flows, the yield to maturity needs to be calculated to be used as
discount rate.
Yield to maturity = [(C+ (F-P))/n] / [F+P]/2
= [50 + (0/22)] / [2000/2]

= 5%
The Duration of bond is calculated as follows:
Period Cash flow Period*cash flow PV @ 5%
Present value of
cash flow
1 $ 50 $ 50 $ 0.952 $ 47.62
2 $ 50 $ 100 $ 0.907 $ 90.70
3 $ 50 $ 150 $ 0.864 $ 129.58
4 $ 50 $ 200 $ 0.823 $ 164.54
5 $ 50 $ 250 $ 0.784 $ 195.88
6 $ 50 $ 300 $ 0.746 $ 223.86
7 $ 50 $ 350 $ 0.711 $ 248.74
8 $ 50 $ 400 $ 0.677 $ 270.74
9 $ 50 $ 450 $ 0.645 $ 290.07
10 $ 50 $ 500 $ 0.614 $ 306.96
11 $ 50 $ 550 $ 0.585 $ 321.57
12 $ 50 $ 600 $ 0.557 $ 334.10
13 $ 50 $ 650 $ 0.530 $ 344.71
14 $ 50 $ 700 $ 0.505 $ 353.55
15 $ 50 $ 750 $ 0.481 $ 360.76
16 $ 50 $ 800 $ 0.458 $ 366.49
17 $ 50 $ 850 $ 0.436 $ 370.85
18 $ 50 $ 900 $ 0.416 $ 373.97
19 $ 50 $ 950 $ 0.396 $ 375.95
20 $ 50 $ 1,000 $ 0.377 $ 376.89
21 $ 50 $ 1,050 $ 0.359 $ 376.89
22 $ 1,050 $ 23,100 $ 0.342 $ 7,896.73
Total $ 13,821.15
Macauley Duration of bond = 13821.15 / 1000
= 13.82 years
Modified Duration = Macauley Duration / (1+yield to maturity)
= 13.82 / 6%
= 13.16
Dollar duration = -modified duration * (bond price / 100)
= -13.16*(1000/100)
The Duration of bond is calculated as follows:
Period Cash flow Period*cash flow PV @ 5%
Present value of
cash flow
1 $ 50 $ 50 $ 0.952 $ 47.62
2 $ 50 $ 100 $ 0.907 $ 90.70
3 $ 50 $ 150 $ 0.864 $ 129.58
4 $ 50 $ 200 $ 0.823 $ 164.54
5 $ 50 $ 250 $ 0.784 $ 195.88
6 $ 50 $ 300 $ 0.746 $ 223.86
7 $ 50 $ 350 $ 0.711 $ 248.74
8 $ 50 $ 400 $ 0.677 $ 270.74
9 $ 50 $ 450 $ 0.645 $ 290.07
10 $ 50 $ 500 $ 0.614 $ 306.96
11 $ 50 $ 550 $ 0.585 $ 321.57
12 $ 50 $ 600 $ 0.557 $ 334.10
13 $ 50 $ 650 $ 0.530 $ 344.71
14 $ 50 $ 700 $ 0.505 $ 353.55
15 $ 50 $ 750 $ 0.481 $ 360.76
16 $ 50 $ 800 $ 0.458 $ 366.49
17 $ 50 $ 850 $ 0.436 $ 370.85
18 $ 50 $ 900 $ 0.416 $ 373.97
19 $ 50 $ 950 $ 0.396 $ 375.95
20 $ 50 $ 1,000 $ 0.377 $ 376.89
21 $ 50 $ 1,050 $ 0.359 $ 376.89
22 $ 1,050 $ 23,100 $ 0.342 $ 7,896.73
Total $ 13,821.15
Macauley Duration of bond = 13821.15 / 1000
= 13.82 years
Modified Duration = Macauley Duration / (1+yield to maturity)
= 13.82 / 6%
= 13.16
Dollar duration = -modified duration * (bond price / 100)
= -13.16*(1000/100)
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

= $131.6
b) Estimated price change on the bond if the interest rate increases by 0.1% = 13.82*0.1%
= 1.38%
New bond price = 1000-(1.38%*1000)
= $986.18
Estimated price change on the bond if the interest rate decreases by 0.2% = 13.82*0.2%
= 2.76%
New bond price = 1000 + (2.76%*1000)
= $1,027.64
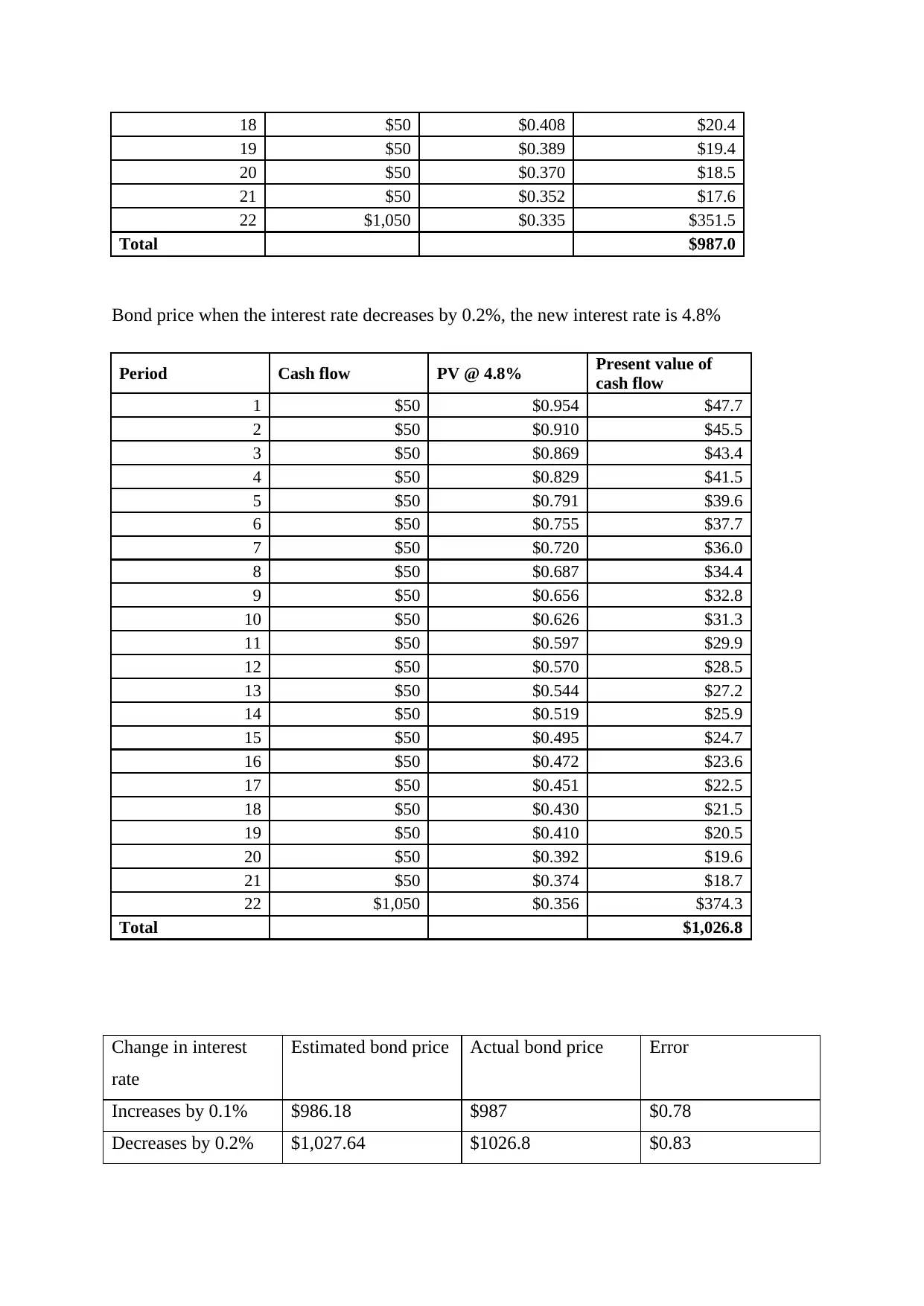
c) Actual bond price using traditional present value bond pricing technique
When interest rate increases by 0.1%, the new yield is 5.1%.
Period Cash flow PV @ 5.1% Present value of cash
flow
1 $50 $0.951 $47.6
2 $50 $0.905 $45.3
3 $50 $0.861 $43.1
4 $50 $0.820 $41.0
5 $50 $0.780 $39.0
6 $50 $0.742 $37.1
7 $50 $0.706 $35.3
8 $50 $0.672 $33.6
9 $50 $0.639 $32.0
10 $50 $0.608 $30.4
11 $50 $0.579 $28.9
12 $50 $0.551 $27.5
13 $50 $0.524 $26.2
14 $50 $0.498 $24.9
15 $50 $0.474 $23.7
16 $50 $0.451 $22.6
17 $50 $0.429 $21.5
b) Estimated price change on the bond if the interest rate increases by 0.1% = 13.82*0.1%
= 1.38%
New bond price = 1000-(1.38%*1000)
= $986.18
Estimated price change on the bond if the interest rate decreases by 0.2% = 13.82*0.2%
= 2.76%
New bond price = 1000 + (2.76%*1000)
= $1,027.64
c) Actual bond price using traditional present value bond pricing technique
When interest rate increases by 0.1%, the new yield is 5.1%.
Period Cash flow PV @ 5.1% Present value of cash
flow
1 $50 $0.951 $47.6
2 $50 $0.905 $45.3
3 $50 $0.861 $43.1
4 $50 $0.820 $41.0
5 $50 $0.780 $39.0
6 $50 $0.742 $37.1
7 $50 $0.706 $35.3
8 $50 $0.672 $33.6
9 $50 $0.639 $32.0
10 $50 $0.608 $30.4
11 $50 $0.579 $28.9
12 $50 $0.551 $27.5
13 $50 $0.524 $26.2
14 $50 $0.498 $24.9
15 $50 $0.474 $23.7
16 $50 $0.451 $22.6
17 $50 $0.429 $21.5
18 $50 $0.408 $20.4
19 $50 $0.389 $19.4
20 $50 $0.370 $18.5
21 $50 $0.352 $17.6
22 $1,050 $0.335 $351.5
Total $987.0
Bond price when the interest rate decreases by 0.2%, the new interest rate is 4.8%
Period Cash flow PV @ 4.8% Present value of
cash flow
1 $50 $0.954 $47.7
2 $50 $0.910 $45.5
3 $50 $0.869 $43.4
4 $50 $0.829 $41.5
5 $50 $0.791 $39.6
6 $50 $0.755 $37.7
7 $50 $0.720 $36.0
8 $50 $0.687 $34.4
9 $50 $0.656 $32.8
10 $50 $0.626 $31.3
11 $50 $0.597 $29.9
12 $50 $0.570 $28.5
13 $50 $0.544 $27.2
14 $50 $0.519 $25.9
15 $50 $0.495 $24.7
16 $50 $0.472 $23.6
17 $50 $0.451 $22.5
18 $50 $0.430 $21.5
19 $50 $0.410 $20.5
20 $50 $0.392 $19.6
21 $50 $0.374 $18.7
22 $1,050 $0.356 $374.3
Total $1,026.8
Change in interest
rate
Estimated bond price Actual bond price Error
Increases by 0.1% $986.18 $987 $0.78
Decreases by 0.2% $1,027.64 $1026.8 $0.83
19 $50 $0.389 $19.4
20 $50 $0.370 $18.5
21 $50 $0.352 $17.6
22 $1,050 $0.335 $351.5
Total $987.0
Bond price when the interest rate decreases by 0.2%, the new interest rate is 4.8%
Period Cash flow PV @ 4.8% Present value of
cash flow
1 $50 $0.954 $47.7
2 $50 $0.910 $45.5
3 $50 $0.869 $43.4
4 $50 $0.829 $41.5
5 $50 $0.791 $39.6
6 $50 $0.755 $37.7
7 $50 $0.720 $36.0
8 $50 $0.687 $34.4
9 $50 $0.656 $32.8
10 $50 $0.626 $31.3
11 $50 $0.597 $29.9
12 $50 $0.570 $28.5
13 $50 $0.544 $27.2
14 $50 $0.519 $25.9
15 $50 $0.495 $24.7
16 $50 $0.472 $23.6
17 $50 $0.451 $22.5
18 $50 $0.430 $21.5
19 $50 $0.410 $20.5
20 $50 $0.392 $19.6
21 $50 $0.374 $18.7
22 $1,050 $0.356 $374.3
Total $1,026.8
Change in interest
rate
Estimated bond price Actual bond price Error
Increases by 0.1% $986.18 $987 $0.78
Decreases by 0.2% $1,027.64 $1026.8 $0.83

From the above we see that the change in the estimated bond price is higher than the actual
bond price. This error occurs because the estimated price due to change in interest rate is due
to the interest rate elasticity of the bond.
Question 4
Dividend paid = $0.2, rate of return = 16%, growth rate = 8%
Value of share = expected dividend / (rate of return – growth rate)
= (0.2*1.08) / (0.16-0.08)
= $2.7
Price of the stock in five years = dividend in year 5 / (rate of return – growth rate)
Dividend in year 5
Year
Expected
dividend
1 $0.216
2 $0.233
3 $0.251
4 $0.272
5 $0.293
Value of share = 0.293 / 0.08
= $3.67
Price of share with growth rate being 20% for next three years and 8% thereafter.
Expected dividend for the high growth phase:
Year Growth rate
Expected
dividend
0 $0.2
1 20% $0.24
2 20% $0.28
bond price. This error occurs because the estimated price due to change in interest rate is due
to the interest rate elasticity of the bond.
Question 4
Dividend paid = $0.2, rate of return = 16%, growth rate = 8%
Value of share = expected dividend / (rate of return – growth rate)
= (0.2*1.08) / (0.16-0.08)
= $2.7
Price of the stock in five years = dividend in year 5 / (rate of return – growth rate)
Dividend in year 5
Year
Expected
dividend
1 $0.216
2 $0.233
3 $0.251
4 $0.272
5 $0.293
Value of share = 0.293 / 0.08
= $3.67
Price of share with growth rate being 20% for next three years and 8% thereafter.
Expected dividend for the high growth phase:
Year Growth rate
Expected
dividend
0 $0.2
1 20% $0.24
2 20% $0.28
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
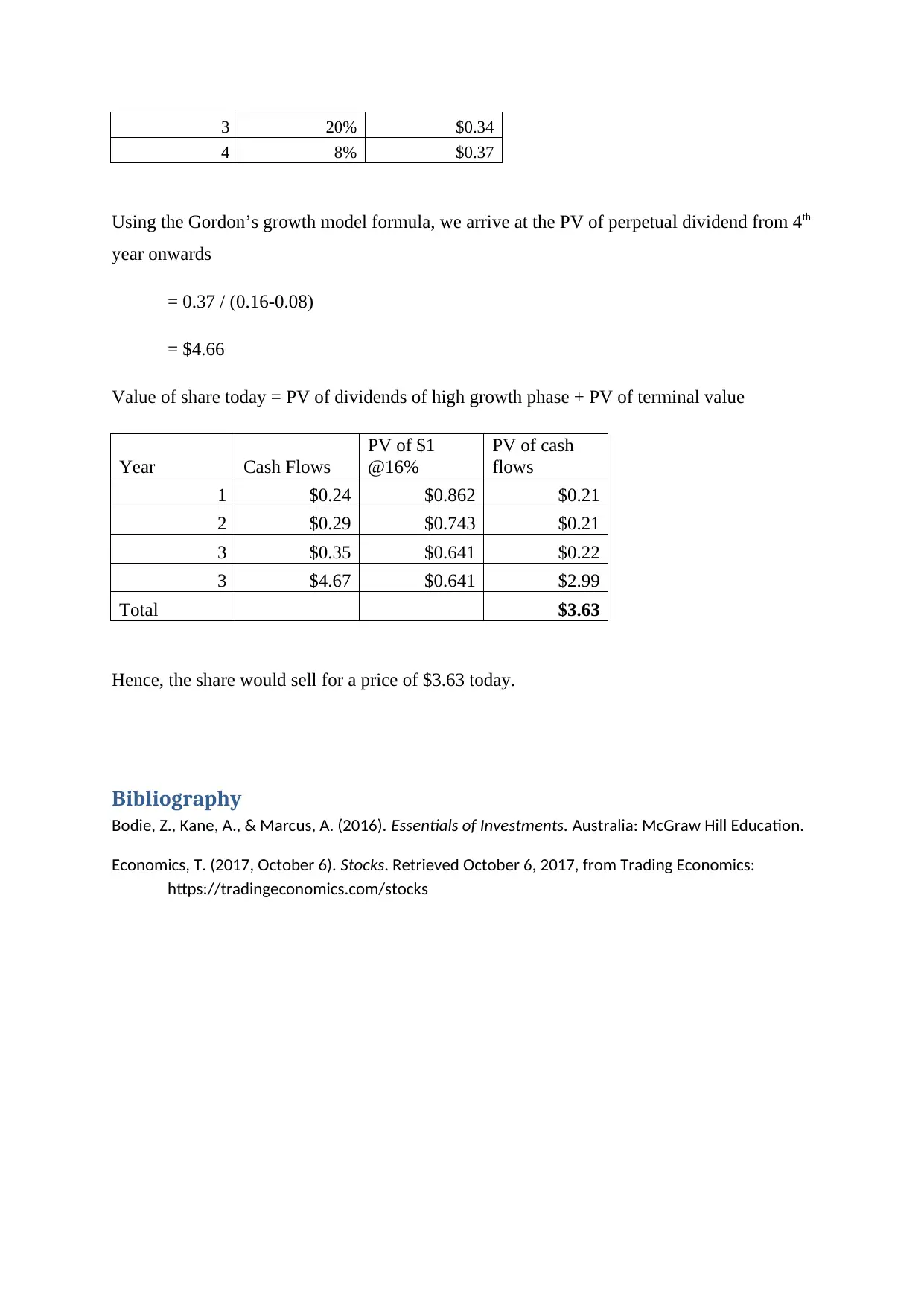
3 20% $0.34
4 8% $0.37
Using the Gordon’s growth model formula, we arrive at the PV of perpetual dividend from 4th
year onwards
= 0.37 / (0.16-0.08)
= $4.66
Value of share today = PV of dividends of high growth phase + PV of terminal value
Year Cash Flows
PV of $1
@16%
PV of cash
flows
1 $0.24 $0.862 $0.21
2 $0.29 $0.743 $0.21
3 $0.35 $0.641 $0.22
3 $4.67 $0.641 $2.99
Total $3.63
Hence, the share would sell for a price of $3.63 today.
Bibliography
Bodie, Z., Kane, A., & Marcus, A. (2016). Essentials of Investments. Australia: McGraw Hill Education.
Economics, T. (2017, October 6). Stocks. Retrieved October 6, 2017, from Trading Economics:
https://tradingeconomics.com/stocks
4 8% $0.37
Using the Gordon’s growth model formula, we arrive at the PV of perpetual dividend from 4th
year onwards
= 0.37 / (0.16-0.08)
= $4.66
Value of share today = PV of dividends of high growth phase + PV of terminal value
Year Cash Flows
PV of $1
@16%
PV of cash
flows
1 $0.24 $0.862 $0.21
2 $0.29 $0.743 $0.21
3 $0.35 $0.641 $0.22
3 $4.67 $0.641 $2.99
Total $3.63
Hence, the share would sell for a price of $3.63 today.
Bibliography
Bodie, Z., Kane, A., & Marcus, A. (2016). Essentials of Investments. Australia: McGraw Hill Education.
Economics, T. (2017, October 6). Stocks. Retrieved October 6, 2017, from Trading Economics:
https://tradingeconomics.com/stocks
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





