Analysis of Johnson and Johnson Stock on NYSE
VerifiedAdded on 2023/06/13
|11
|1053
|145
AI Summary
This report provides an analysis of Johnson and Johnson stock on NYSE from January 1984 to December 2003. It includes descriptive statistics, time series plots, normality test, and estimation output of Fama French Model 1993 and Five Factor Model.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

qwertyuiopasdfghjklzxcvbnmqwertyui
opasdfghjklzxcvbnmqwertyuiopasdfgh
jklzxcvbnmqwertyuiopasdfghjklzxcvb
nmqwertyuiopasdfghjklzxcvbnmqwer
tyuiopasdfghjklzxcvbnmqwertyuiopas
dfghjklzxcvbnmqwertyuiopasdfghjklzx
cvbnmqwertyuiopasdfghjklzxcvbnmq
wertyuiopasdfghjklzxcvbnmqwertyuio
pasdfghjklzxcvbnmqwertyuiopasdfghj
klzxcvbnmqwertyuiopasdfghjklzxcvbn
mqwertyuiopasdfghjklzxcvbnmqwerty
uiopasdfghjklzxcvbnmqwertyuiopasdf
ghjklzxcvbnmqwertyuiopasdfghjklzxc
vbnmqwertyuiopasdfghjklzxcvbnmrty
uiopasdfghjklzxcvbnmqwertyuiopasdf
ghjklzxcvbnmqwertyuiopasdfghjklzxc
[Type the document title]
[Type the document subtitle]
[Pick the date]
Geeta
opasdfghjklzxcvbnmqwertyuiopasdfgh
jklzxcvbnmqwertyuiopasdfghjklzxcvb
nmqwertyuiopasdfghjklzxcvbnmqwer
tyuiopasdfghjklzxcvbnmqwertyuiopas
dfghjklzxcvbnmqwertyuiopasdfghjklzx
cvbnmqwertyuiopasdfghjklzxcvbnmq
wertyuiopasdfghjklzxcvbnmqwertyuio
pasdfghjklzxcvbnmqwertyuiopasdfghj
klzxcvbnmqwertyuiopasdfghjklzxcvbn
mqwertyuiopasdfghjklzxcvbnmqwerty
uiopasdfghjklzxcvbnmqwertyuiopasdf
ghjklzxcvbnmqwertyuiopasdfghjklzxc
vbnmqwertyuiopasdfghjklzxcvbnmrty
uiopasdfghjklzxcvbnmqwertyuiopasdf
ghjklzxcvbnmqwertyuiopasdfghjklzxc
[Type the document title]
[Type the document subtitle]
[Pick the date]
Geeta
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Contents
Task A..........................................................................................................................................................3
Task B..........................................................................................................................................................8
Bibliography...............................................................................................................................................11
Task A..........................................................................................................................................................3
Task B..........................................................................................................................................................8
Bibliography...............................................................................................................................................11

The stock given for this assignment in Johnson and Johnson on NYSE and the sub-period given is
numbers 241 to 480. Thus, the observation period is January 1984 to December 2003.
Task A
1) Vaariable Rf denotes the return on a 1 month Treasury Bill and is the most stable
indicator of returns. This is the estimated return on the bond and serves as the expected
return on the stock
Using the Asset Pricing Model, we derive the price returns as follows
r = Rf + BiRmRf
In order to derive the logarithmic returns, the returns on price levels were transformed using
the log function.
Table 1: Descriptive Statistics for prices and price Returns
JNJ LN_PRICE...
Mean 66.56687 0.001244
Median 63.55500 0.014061
Maximum 114.5000 0.172328
Minimum 29.25000 -0.772330
Std. Dev. 20.06444 0.113122
Skewness 0.252545 -3.912957
Kurtosis 1.923759 25.17210
Jarque-Bera 14.13411 5505.435
Probability 0.000853 0.000000
Sum 15976.05 0.297278
Sum Sq. Dev. 96217.04 3.045613
Observations 240 239
numbers 241 to 480. Thus, the observation period is January 1984 to December 2003.
Task A
1) Vaariable Rf denotes the return on a 1 month Treasury Bill and is the most stable
indicator of returns. This is the estimated return on the bond and serves as the expected
return on the stock
Using the Asset Pricing Model, we derive the price returns as follows
r = Rf + BiRmRf
In order to derive the logarithmic returns, the returns on price levels were transformed using
the log function.
Table 1: Descriptive Statistics for prices and price Returns
JNJ LN_PRICE...
Mean 66.56687 0.001244
Median 63.55500 0.014061
Maximum 114.5000 0.172328
Minimum 29.25000 -0.772330
Std. Dev. 20.06444 0.113122
Skewness 0.252545 -3.912957
Kurtosis 1.923759 25.17210
Jarque-Bera 14.13411 5505.435
Probability 0.000853 0.000000
Sum 15976.05 0.297278
Sum Sq. Dev. 96217.04 3.045613
Observations 240 239
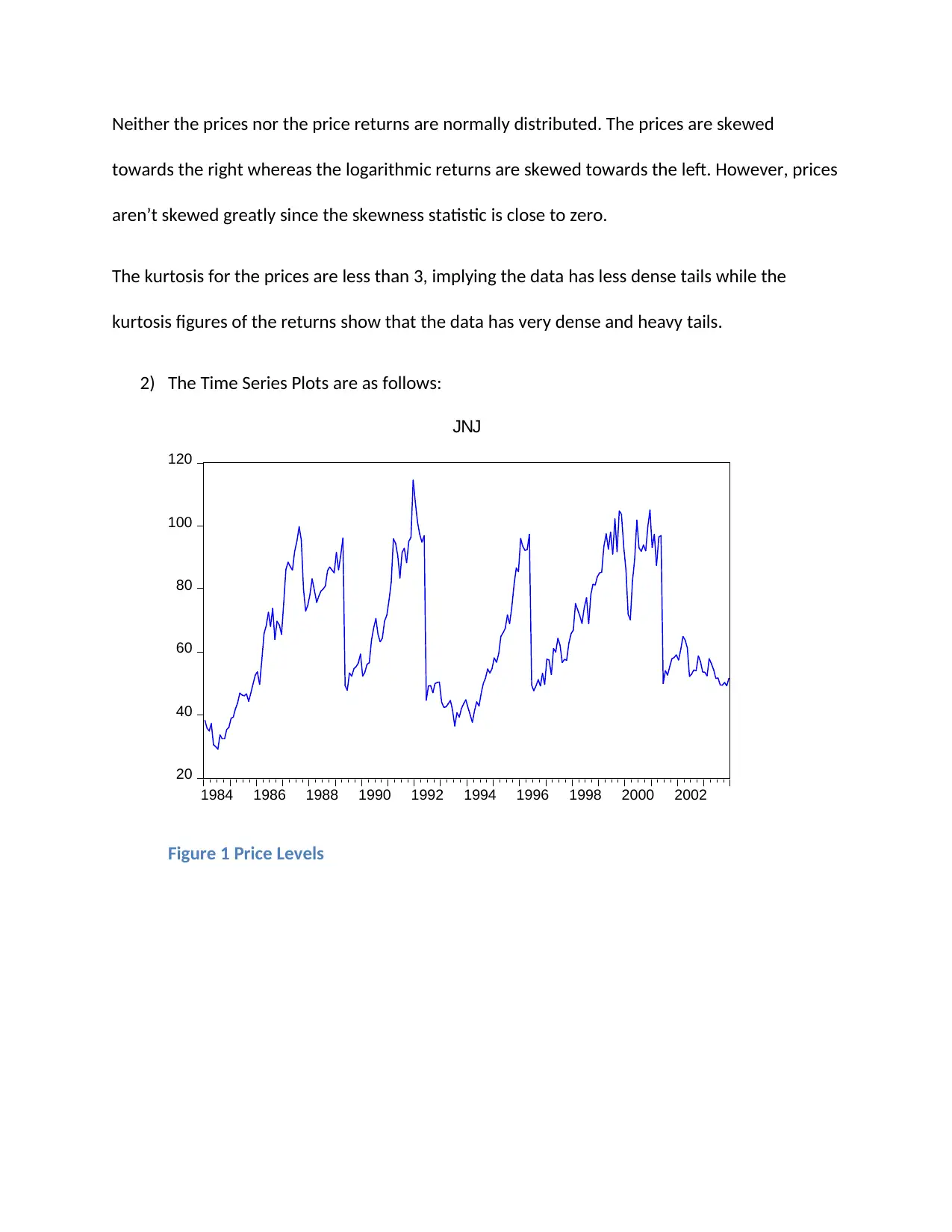
Neither the prices nor the price returns are normally distributed. The prices are skewed
towards the right whereas the logarithmic returns are skewed towards the left. However, prices
aren’t skewed greatly since the skewness statistic is close to zero.
The kurtosis for the prices are less than 3, implying the data has less dense tails while the
kurtosis figures of the returns show that the data has very dense and heavy tails.
2) The Time Series Plots are as follows:
20
40
60
80
100
120
1984 1986 1988 1990 1992 1994 1996 1998 2000 2002
JNJ
Figure 1 Price Levels
towards the right whereas the logarithmic returns are skewed towards the left. However, prices
aren’t skewed greatly since the skewness statistic is close to zero.
The kurtosis for the prices are less than 3, implying the data has less dense tails while the
kurtosis figures of the returns show that the data has very dense and heavy tails.
2) The Time Series Plots are as follows:
20
40
60
80
100
120
1984 1986 1988 1990 1992 1994 1996 1998 2000 2002
JNJ
Figure 1 Price Levels
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
-.8
-.6
-.4
-.2
.0
.2
1984 1986 1988 1990 1992 1994 1996 1998 2000 2002
LN_PRICE_RETURNS
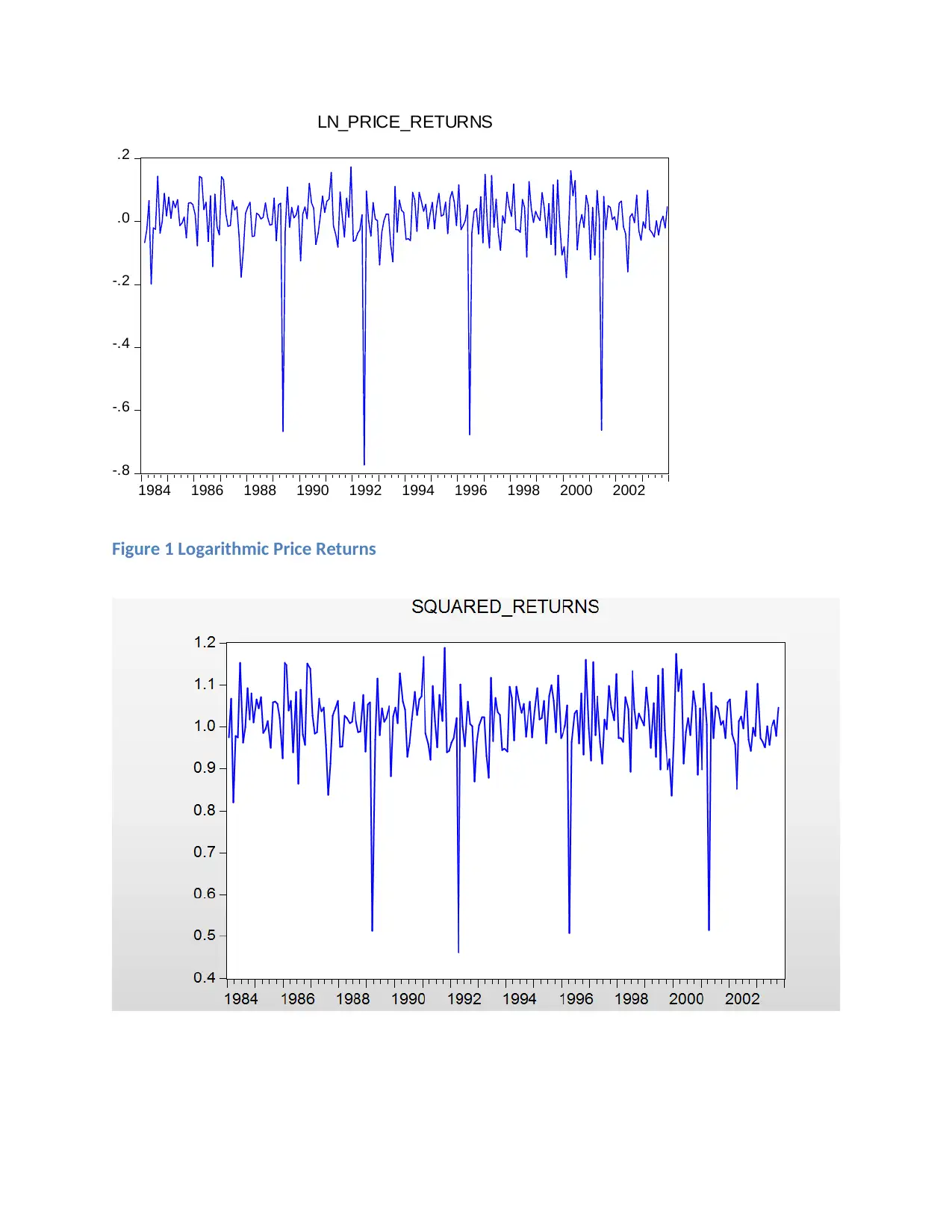
Figure 1 Logarithmic Price Returns
-.6
-.4
-.2
.0
.2
1984 1986 1988 1990 1992 1994 1996 1998 2000 2002
LN_PRICE_RETURNS
Figure 1 Logarithmic Price Returns

Figure 3 Squared Logarithmic Returns
The logarithmic plots were squared to get the logarithmic returns.
Price levels show a great deal of volatility but nor as much as the returns or the squared
returns. The returns and the squared returns are much closely distributed than the price
levels. The higher volatility in the price returns, instead of the prices symbolizes that the
market may see the stock as trustworthy. However, from a primary observation, the
returns and squared returns seem stationary around a mean. Thus, it is possible the high
volatility may be due to the hgh volumes of trade.
3) In order to test for the normality we deducted the logarithmic returns from market(ln_rf)
from the market (ln_price_returns) and plot a histogram. There are various ways to test for
normality but the histogram is a pictorial representation of the numbers.
The logarithmic plots were squared to get the logarithmic returns.
Price levels show a great deal of volatility but nor as much as the returns or the squared
returns. The returns and the squared returns are much closely distributed than the price
levels. The higher volatility in the price returns, instead of the prices symbolizes that the
market may see the stock as trustworthy. However, from a primary observation, the
returns and squared returns seem stationary around a mean. Thus, it is possible the high
volatility may be due to the hgh volumes of trade.
3) In order to test for the normality we deducted the logarithmic returns from market(ln_rf)
from the market (ln_price_returns) and plot a histogram. There are various ways to test for
normality but the histogram is a pictorial representation of the numbers.
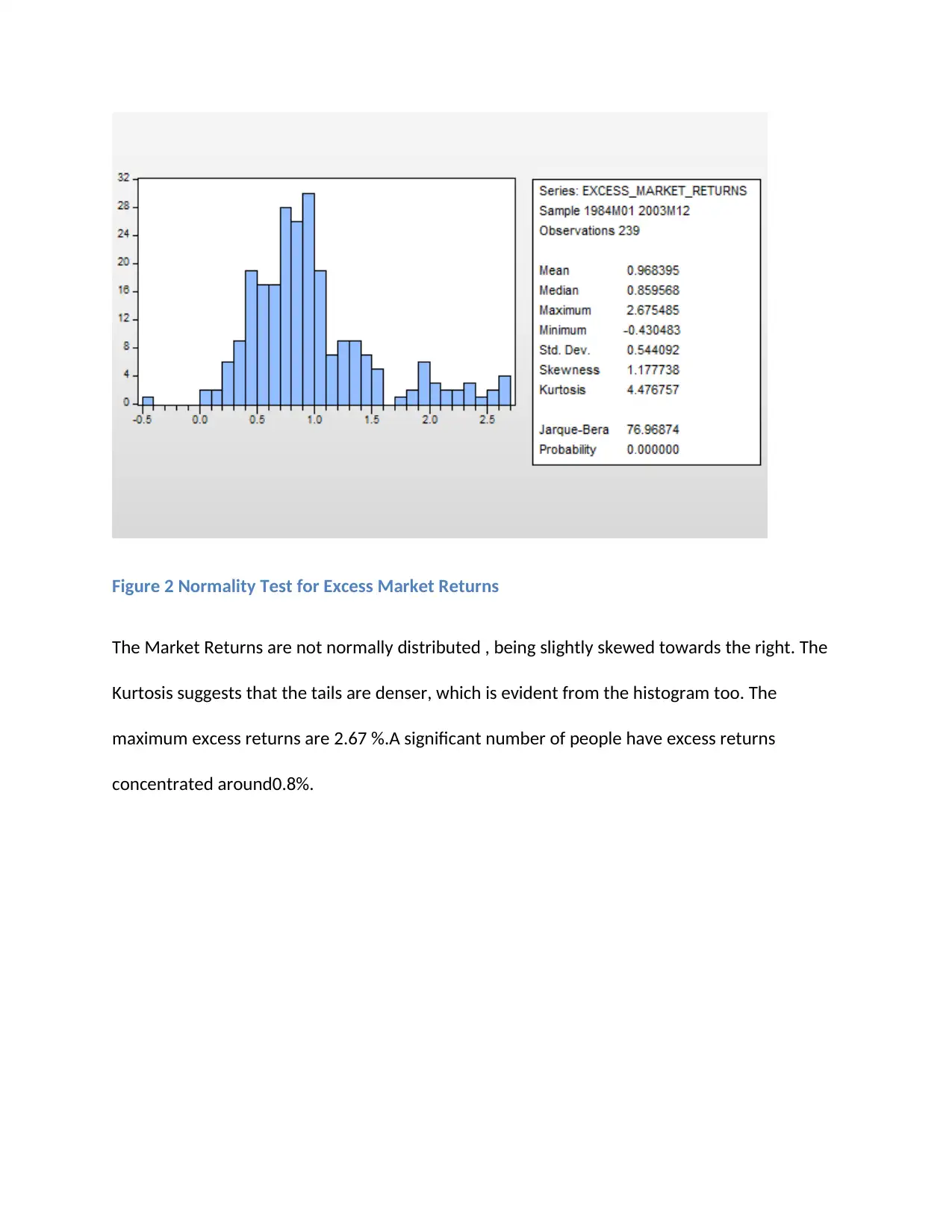
Figure 2 Normality Test for Excess Market Returns
The Market Returns are not normally distributed , being slightly skewed towards the right. The
Kurtosis suggests that the tails are denser, which is evident from the histogram too. The
maximum excess returns are 2.67 %.A significant number of people have excess returns
concentrated around0.8%.
The Market Returns are not normally distributed , being slightly skewed towards the right. The
Kurtosis suggests that the tails are denser, which is evident from the histogram too. The
maximum excess returns are 2.67 %.A significant number of people have excess returns
concentrated around0.8%.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
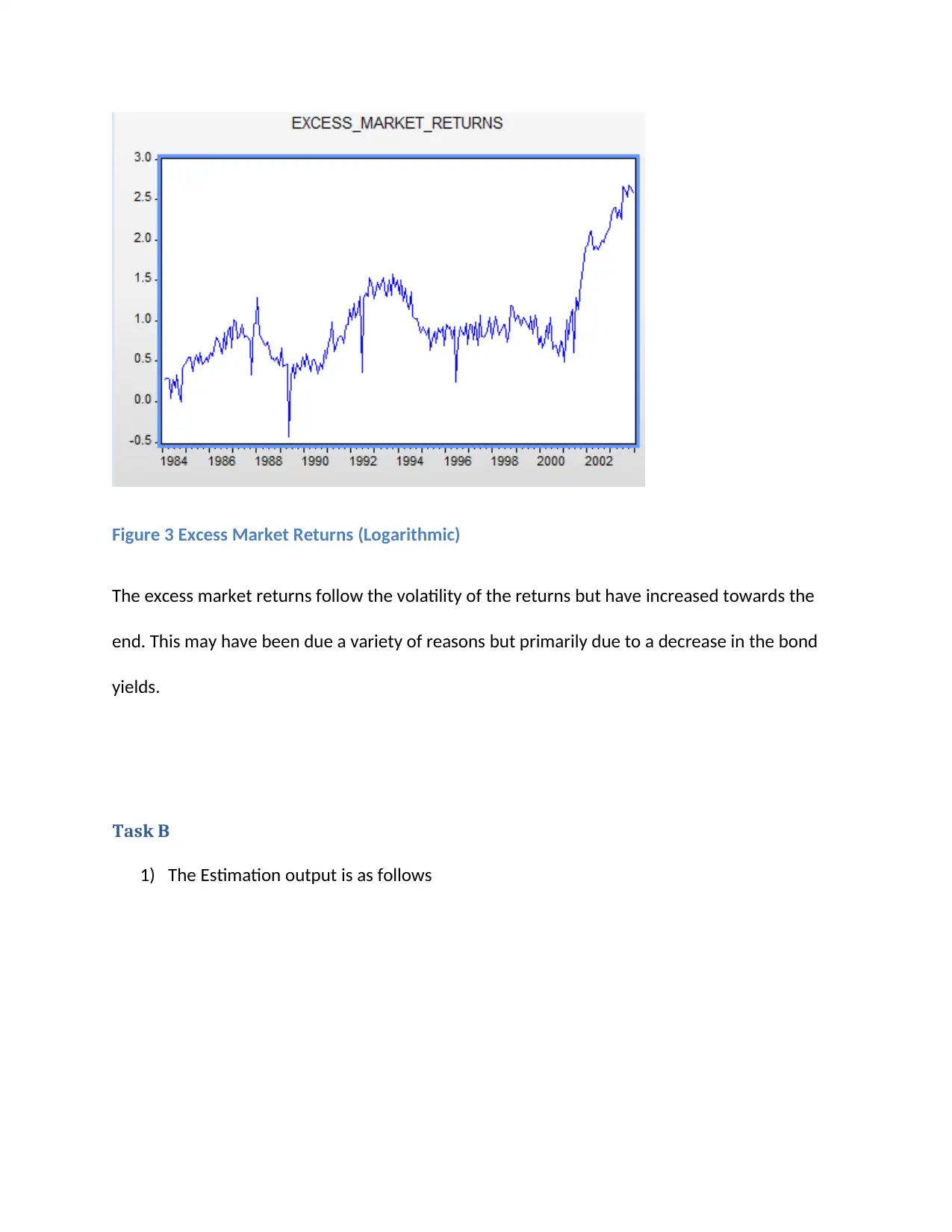
Figure 3 Excess Market Returns (Logarithmic)
The excess market returns follow the volatility of the returns but have increased towards the
end. This may have been due a variety of reasons but primarily due to a decrease in the bond
yields.
Task B
1) The Estimation output is as follows
The excess market returns follow the volatility of the returns but have increased towards the
end. This may have been due a variety of reasons but primarily due to a decrease in the bond
yields.
Task B
1) The Estimation output is as follows

Table 2 Least Square Estimate of Fama French Model 1993
In this equation R is the return on 1 month Treasury Bills
RF is the is the difference between the average return on two conservative investment
portfolios and two aggressive investment portfolios,
Rm-Rf is the excess return on the market, value-weight return
SMB (Small Minus Big) is the average return on the nine small stock portfolios minus the
average return on the nine big stock portfolios
(Fama & French, 1993 (3))
In order to test the significances individually, we test the t-statistic and the prob-statistic(last
colum of the output). The column “prob” describes the significance of each variable and all
variable are significant. However, the impact of the variable can be determined from the t –
statistic. The variable of (rm-rf) has a greater impact than predicted, the variable SMB has
slightly greater impact while the variable HML has a slightly lower impact than predicted.
In this equation R is the return on 1 month Treasury Bills
RF is the is the difference between the average return on two conservative investment
portfolios and two aggressive investment portfolios,
Rm-Rf is the excess return on the market, value-weight return
SMB (Small Minus Big) is the average return on the nine small stock portfolios minus the
average return on the nine big stock portfolios
(Fama & French, 1993 (3))
In order to test the significances individually, we test the t-statistic and the prob-statistic(last
colum of the output). The column “prob” describes the significance of each variable and all
variable are significant. However, the impact of the variable can be determined from the t –
statistic. The variable of (rm-rf) has a greater impact than predicted, the variable SMB has
slightly greater impact while the variable HML has a slightly lower impact than predicted.

To test the significance further, the F- statistic is reviewed. Results are significant for the Fama-
French three factor model. However, individually, results are most significant for Excess Market
Returns(rm_rf). Results are also significant when they are taken without the intercept i.e
without the bond yields.
5) The Five Factor Model is as follows:
Rit - RFt = ai + β1(RMt – RFt) + β2SMBt + β3HMLt + eit. (Fama & French,2015)
In this equation, HML (High Minus Low) is the average return on the two value
portfolios minus the average return on the two growth portfolios
RMW (Robust Minus Weak) is the average return on the two robust operating
profitability portfolios minus the average return on the two weak operating profitability
The Estimation Output is as follows
French three factor model. However, individually, results are most significant for Excess Market
Returns(rm_rf). Results are also significant when they are taken without the intercept i.e
without the bond yields.
5) The Five Factor Model is as follows:
Rit - RFt = ai + β1(RMt – RFt) + β2SMBt + β3HMLt + eit. (Fama & French,2015)
In this equation, HML (High Minus Low) is the average return on the two value
portfolios minus the average return on the two growth portfolios
RMW (Robust Minus Weak) is the average return on the two robust operating
profitability portfolios minus the average return on the two weak operating profitability
The Estimation Output is as follows
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Table 3 Least Square Estimation of the Fama Five Factor Model
The R- square of this model is a perfect 1 implying that the five factor model is a perfect fit and
the best model to use.
Bibliography
Fama, E., & French, K. (1993 (3)). Common risk factors in the returns on stocks and bonds. Journal of
Financial Economics, 3– 56.
Fama, E., & French, K. (2015). A five-factor asset pricing model. Journal of Financial Economics, 1– 22.
The R- square of this model is a perfect 1 implying that the five factor model is a perfect fit and
the best model to use.
Bibliography
Fama, E., & French, K. (1993 (3)). Common risk factors in the returns on stocks and bonds. Journal of
Financial Economics, 3– 56.
Fama, E., & French, K. (2015). A five-factor asset pricing model. Journal of Financial Economics, 1– 22.
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.