Evaluation of deterministic state-of-the-art forecasting approaches for project duration based on earned value management
VerifiedAdded on 2023/02/01
|9
|10209
|66
AI Summary
This article evaluates the accuracy and timeliness of three deterministic techniques for forecasting project duration based on earned value management. The results indicate that all three techniques are relevant and have the potential to improve project forecasting.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Evaluation of deterministic state-of-the-art forecasting
approaches for project duration based on earned
value management
Jordy Batseliera, Mario Vanhouckea, b, c,⁎
a Faculty of Economics and Business Administration, Ghent University, Tweekerkenstraat 2, 9000 Ghent, Belgium
b Technology and Operations Management Area, Vlerick Business School, Reep 1, 9000 Ghent, Belgium
c Department of Management Science and Innovation, University College London, Gower Street, London WC1E 6BT, United Kingd
Received 15 January 2015; received in revised form 8 April 2015; accepted 14 April 2015
Abstract
In recent years, a variety of novel approaches for fulfilling the important management task of accurately forecasting pro
proposed, with many of them based on the earned value management (EVM) methodology. However, these state-of-the-a
not been adequately tested on a large database, nor has their validity been empirically proven. Therefore, we evaluate the
of three promising deterministic techniques and their mutualcombinations on a real-life projectdatabase.More specifically,two techniques
respectively integrate rework and activity sensitivity in EVM time forecasting as extensions,while a third innovatively calculates schedule
performance from time-based metrics and is appropriately called earned duration management or EDM(t). The results indi
considered techniques are relevant. More concretely, the two EVM extensions exhibit accuracy-enhancing power for differe
EDM(t) performs very similar to the best EVM methods and shows potential to improve them.
© 2015 Elsevier Ltd. APM and IPMA. All rights reserved.
Keywords: Project management; Time forecasting;Earned value management; Earned duration management; Rework; Sensitivity measures;Empiricaldatabase;
Project control
1. Introduction
Being ableto accurately predictthe final duration of
a projectis essentialto good projectmanagement.The
widely-used project control technique of earned value manage-
ment(EVM) providesa basisfor obtainingsuch project
durationforecasts.A presentationof the basicand more
thoroughgoing aspects of the EVM methodology can be found
in several works (Anbari, 2003; Fleming and Koppelman, 2010;
PMI, 2008;Vanhoucke,2010a,2014).The traditionalEVM
time1 forecasting approaches — the planned value metho
(PVM) by Anbari (2003),the earneddurationmethod
(EDM) by Jacob and Kane (2004) and the earned schedule
method (ESM)by Lipke (2003)— have recently been
evaluated by Batselier and Vanhoucke (2015b) based on
real-life project databaseconstructedby Batselierand
Vanhoucke (2015a).The said empiricalresearch supported
the findingsof the simulation study ofVanhouckeand
Vandevoorde (2007)by also indicating ESM as the most
accurate method.
⁎ Corresponding author at: Faculty of Economics and Business Administration,
Ghent University, Tweekerkenstraat 2, 9000 Ghent, Belgium. Tel.: + 32 9 264 35
69.
E-mail addresses: jordy.batselier@ugent.be (J. Batselier),
mario.vanhoucke@ugent.be (M. Vanhoucke).
1 Following earlierworks related to this paper(Batselierand Vanhoucke,
2015b;Elshaer,2013;Khamooshiand Golafshani,2014;Vanhoucke and
Vandevoorde, 2007, etc.), the terms “time” and “duration” are intercha
when used in the contextof EVM forecasting(apartfrom linguistic
preferences).
www.elsevier.com/locate/ijproman
http://dx.doi.org/10.1016/j.ijproman.2015.04.003
0263-7863/00/© 2015 Elsevier Ltd. APM and IPMA. All rights reserved.
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Available online at www.sciencedirect.com
ScienceDirect
International Journal of Project Management xx (2015) xxx – xxx
JPMA-01764; No of Pages 9
approaches for project duration based on earned
value management
Jordy Batseliera, Mario Vanhouckea, b, c,⁎
a Faculty of Economics and Business Administration, Ghent University, Tweekerkenstraat 2, 9000 Ghent, Belgium
b Technology and Operations Management Area, Vlerick Business School, Reep 1, 9000 Ghent, Belgium
c Department of Management Science and Innovation, University College London, Gower Street, London WC1E 6BT, United Kingd
Received 15 January 2015; received in revised form 8 April 2015; accepted 14 April 2015
Abstract
In recent years, a variety of novel approaches for fulfilling the important management task of accurately forecasting pro
proposed, with many of them based on the earned value management (EVM) methodology. However, these state-of-the-a
not been adequately tested on a large database, nor has their validity been empirically proven. Therefore, we evaluate the
of three promising deterministic techniques and their mutualcombinations on a real-life projectdatabase.More specifically,two techniques
respectively integrate rework and activity sensitivity in EVM time forecasting as extensions,while a third innovatively calculates schedule
performance from time-based metrics and is appropriately called earned duration management or EDM(t). The results indi
considered techniques are relevant. More concretely, the two EVM extensions exhibit accuracy-enhancing power for differe
EDM(t) performs very similar to the best EVM methods and shows potential to improve them.
© 2015 Elsevier Ltd. APM and IPMA. All rights reserved.
Keywords: Project management; Time forecasting;Earned value management; Earned duration management; Rework; Sensitivity measures;Empiricaldatabase;
Project control
1. Introduction
Being ableto accurately predictthe final duration of
a projectis essentialto good projectmanagement.The
widely-used project control technique of earned value manage-
ment(EVM) providesa basisfor obtainingsuch project
durationforecasts.A presentationof the basicand more
thoroughgoing aspects of the EVM methodology can be found
in several works (Anbari, 2003; Fleming and Koppelman, 2010;
PMI, 2008;Vanhoucke,2010a,2014).The traditionalEVM
time1 forecasting approaches — the planned value metho
(PVM) by Anbari (2003),the earneddurationmethod
(EDM) by Jacob and Kane (2004) and the earned schedule
method (ESM)by Lipke (2003)— have recently been
evaluated by Batselier and Vanhoucke (2015b) based on
real-life project databaseconstructedby Batselierand
Vanhoucke (2015a).The said empiricalresearch supported
the findingsof the simulation study ofVanhouckeand
Vandevoorde (2007)by also indicating ESM as the most
accurate method.
⁎ Corresponding author at: Faculty of Economics and Business Administration,
Ghent University, Tweekerkenstraat 2, 9000 Ghent, Belgium. Tel.: + 32 9 264 35
69.
E-mail addresses: jordy.batselier@ugent.be (J. Batselier),
mario.vanhoucke@ugent.be (M. Vanhoucke).
1 Following earlierworks related to this paper(Batselierand Vanhoucke,
2015b;Elshaer,2013;Khamooshiand Golafshani,2014;Vanhoucke and
Vandevoorde, 2007, etc.), the terms “time” and “duration” are intercha
when used in the contextof EVM forecasting(apartfrom linguistic
preferences).
www.elsevier.com/locate/ijproman
http://dx.doi.org/10.1016/j.ijproman.2015.04.003
0263-7863/00/© 2015 Elsevier Ltd. APM and IPMA. All rights reserved.
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Available online at www.sciencedirect.com
ScienceDirect
International Journal of Project Management xx (2015) xxx – xxx
JPMA-01764; No of Pages 9
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

However,a variety of novelEVM-based time forecasting
approaches has been developed in the lastfive years.These
state-of-the-arttechniques can be subdivided into two major
categories,namely deterministic and probabilistic approaches
(Barraza etal., 2004).Deterministic approaches — like the
three traditionalEVM time forecasting methods — yield a
point estimateof the eventualprojectduration,whereas
probabilistic techniquesprovide confidence intervalsand/or
distributions of possible durations.The latter techniques can,
for example,make use of stochastic S-curves,which produce
upper and lower bounds for the range of acceptable outcomes
based on the uncertainty aboutthe predictions (Barraza etal.,
2004).Moreover,an extendingprobabilisticapproachis
provided by thefuzzy methodology,which can overcome
vagueness of data by introducing linguistic terms thatcan be
translated into fuzzy numbers through a membership function
(Naeniet al., 2011).An extensive overview ofthe existing
literature on both deterministic and probabilistic2 approaches is
given by Willemsand Vanhoucke(undersubmission).The
said paper also provides a summary of other recently developed
project forecasting methods, like those based on neural networks
(e.g.Pewdum etal.,2009;Rujirayanyong,2009)and support
vectormachines(e.g. Cheng et al., 2010; Wautersand
Vanhoucke,2014).Although these methods have been proven
useful for making project forecasts, an extensive survey is beyond
the scope of this paper,as the current focus is on deterministic
EVM-based forecasting approaches forprojectduration.More
specifically, three recent and promising techniques are considered.
The logical basic principles on which they build are as follows:
• Lipke (2011) integrates the effectof rework in ESM time
forecasting.
• Elshaer (2013) integrates activity sensitivity information in
ESM time forecasting.
• Khamooshiand Golafshani(2014)introduce earned dura-
tion management or EDM(t)3, where schedule performance
is calculated from metrics expressed in time units (and not in
cost units).
Theselogical basic principlesin fact demonstratethe
relevance ofintroducing the three selected methods.A more
concrete presentation ofthe three techniquesis provided in
Section 2. Moreover, the last two papers in the list above are also
included in the overview of Willems and Vanhoucke (2015), of
course under the category of deterministic approaches.
In the respective papers, all three of the methods are said to
have the potentialto improve the accuracy of the traditional
EVM time forecasting methods. Nevertheless, these assertions
have notyetbeen adequately tested on a large database,nor
has the validity of the considered techniques been empirica
proven.More concretely,Lipke (2011)and Khamooshiand
Golafshani(2014)apply theirtechnique on justone real-life
project, whereas Elshaer (2013) only considers projects gen
by the RanGen project network generator (Demeulemeeste
2003;Vanhouckeet al., 2008)thatwerealready used in
many earlierprojectmanagementstudies(Vandevoorde and
Vanhoucke,2006; Vanhoucke,2010a,2010b,2011,2012;
Vanhoucke and Vandevoorde, 2007).
Moreover, it is not known which one of the three conside
methods — or which combination of the methods — would
the bestresults,overalland in differentstages ofthe project.
Therefore,the goalof this paper is to compare the forecasting
accuracy and timelinessof the three noveltime forecasting
techniques and allof theirmutualcombinations based on the
real-life project data of Batselier and Vanhoucke (2015a). A
recommendations can be made concerning which method
combination of methods — best to use in a certain situation
which future research actionsto take to furtherimprove the
methods' utility.Furthermore,the proposed combination of the
three novel techniques for time forecasting is innovative in
and can therefore also be seen as a contribution of this pap
The remainderof the paperis organized asfollows.In
Section 2, the three considered state-of-the-art time foreca
methods are presented.Section 3 then proposes the methodol-
ogy for evaluating the accuracy and timeliness of these me
on real-lifeprojectdata.Subsequently,the resultsof this
evaluation arepresented and discussed in Section 4.And
finally, in Section 5, conclusions are drawn and suggestions
future research actions are made.
2. Presentation of the three state-of-the-art time forecastin
methods
In this section,the threeconsidered state-of-the-arttime
forecasting methods (Elshaer, 2013; Khamooshi and Golafs
2014;Lipke,2011)are presented in chronologicalorder.The
concerning subsections are assigned a name which reflects
basic principle of the respective method. We restrict oursel
brief explanation ofthe three methods.Although the provided
explanation should suffice forunderstanding the techniques,if
desired,the readercan find more elaborate discussions on the
different methodologies in the originating papers. However
we can present the three novel time forecasting methods —
are all based on EVM — a more general discussion needs to
conducted.
Since earlier studies on EVM forecasting accuracy (Batse
and Vanhoucke,2015b;Vanhoucke and Vandevoorde,2007)
have proven the dominance of ESM over PVM and EDM, the
former method is used as a basis (and benchmark) for all th
novel deterministic approaches.The generic ESM formula for
obtaining the projectduration forecastor estimated time at
completion EAC(t) is given by:
EAC tð Þ ¼ AT þ
PD−ES
P F : ð1Þ
2 In Willems and Vanhoucke (2015), the probabilistic approaches are further
subdivided into stochastic and fuzzy techniques.
3 Khamooshiand Golafshani(2014) in factuse the abbreviation EDM for
earneddurationmanagement.However,this abbreviationwas already
introduced for the earned duration method of Jacob and Kane (2004). In order
to avoid confusion,we therefore referto earned duration managementby
EDM(t). Furthermore, the suffix (t) also clearly indicates that the technique is
based on time metrics instead of cost metrics.
2 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
approaches has been developed in the lastfive years.These
state-of-the-arttechniques can be subdivided into two major
categories,namely deterministic and probabilistic approaches
(Barraza etal., 2004).Deterministic approaches — like the
three traditionalEVM time forecasting methods — yield a
point estimateof the eventualprojectduration,whereas
probabilistic techniquesprovide confidence intervalsand/or
distributions of possible durations.The latter techniques can,
for example,make use of stochastic S-curves,which produce
upper and lower bounds for the range of acceptable outcomes
based on the uncertainty aboutthe predictions (Barraza etal.,
2004).Moreover,an extendingprobabilisticapproachis
provided by thefuzzy methodology,which can overcome
vagueness of data by introducing linguistic terms thatcan be
translated into fuzzy numbers through a membership function
(Naeniet al., 2011).An extensive overview ofthe existing
literature on both deterministic and probabilistic2 approaches is
given by Willemsand Vanhoucke(undersubmission).The
said paper also provides a summary of other recently developed
project forecasting methods, like those based on neural networks
(e.g.Pewdum etal.,2009;Rujirayanyong,2009)and support
vectormachines(e.g. Cheng et al., 2010; Wautersand
Vanhoucke,2014).Although these methods have been proven
useful for making project forecasts, an extensive survey is beyond
the scope of this paper,as the current focus is on deterministic
EVM-based forecasting approaches forprojectduration.More
specifically, three recent and promising techniques are considered.
The logical basic principles on which they build are as follows:
• Lipke (2011) integrates the effectof rework in ESM time
forecasting.
• Elshaer (2013) integrates activity sensitivity information in
ESM time forecasting.
• Khamooshiand Golafshani(2014)introduce earned dura-
tion management or EDM(t)3, where schedule performance
is calculated from metrics expressed in time units (and not in
cost units).
Theselogical basic principlesin fact demonstratethe
relevance ofintroducing the three selected methods.A more
concrete presentation ofthe three techniquesis provided in
Section 2. Moreover, the last two papers in the list above are also
included in the overview of Willems and Vanhoucke (2015), of
course under the category of deterministic approaches.
In the respective papers, all three of the methods are said to
have the potentialto improve the accuracy of the traditional
EVM time forecasting methods. Nevertheless, these assertions
have notyetbeen adequately tested on a large database,nor
has the validity of the considered techniques been empirica
proven.More concretely,Lipke (2011)and Khamooshiand
Golafshani(2014)apply theirtechnique on justone real-life
project, whereas Elshaer (2013) only considers projects gen
by the RanGen project network generator (Demeulemeeste
2003;Vanhouckeet al., 2008)thatwerealready used in
many earlierprojectmanagementstudies(Vandevoorde and
Vanhoucke,2006; Vanhoucke,2010a,2010b,2011,2012;
Vanhoucke and Vandevoorde, 2007).
Moreover, it is not known which one of the three conside
methods — or which combination of the methods — would
the bestresults,overalland in differentstages ofthe project.
Therefore,the goalof this paper is to compare the forecasting
accuracy and timelinessof the three noveltime forecasting
techniques and allof theirmutualcombinations based on the
real-life project data of Batselier and Vanhoucke (2015a). A
recommendations can be made concerning which method
combination of methods — best to use in a certain situation
which future research actionsto take to furtherimprove the
methods' utility.Furthermore,the proposed combination of the
three novel techniques for time forecasting is innovative in
and can therefore also be seen as a contribution of this pap
The remainderof the paperis organized asfollows.In
Section 2, the three considered state-of-the-art time foreca
methods are presented.Section 3 then proposes the methodol-
ogy for evaluating the accuracy and timeliness of these me
on real-lifeprojectdata.Subsequently,the resultsof this
evaluation arepresented and discussed in Section 4.And
finally, in Section 5, conclusions are drawn and suggestions
future research actions are made.
2. Presentation of the three state-of-the-art time forecastin
methods
In this section,the threeconsidered state-of-the-arttime
forecasting methods (Elshaer, 2013; Khamooshi and Golafs
2014;Lipke,2011)are presented in chronologicalorder.The
concerning subsections are assigned a name which reflects
basic principle of the respective method. We restrict oursel
brief explanation ofthe three methods.Although the provided
explanation should suffice forunderstanding the techniques,if
desired,the readercan find more elaborate discussions on the
different methodologies in the originating papers. However
we can present the three novel time forecasting methods —
are all based on EVM — a more general discussion needs to
conducted.
Since earlier studies on EVM forecasting accuracy (Batse
and Vanhoucke,2015b;Vanhoucke and Vandevoorde,2007)
have proven the dominance of ESM over PVM and EDM, the
former method is used as a basis (and benchmark) for all th
novel deterministic approaches.The generic ESM formula for
obtaining the projectduration forecastor estimated time at
completion EAC(t) is given by:
EAC tð Þ ¼ AT þ
PD−ES
P F : ð1Þ
2 In Willems and Vanhoucke (2015), the probabilistic approaches are further
subdivided into stochastic and fuzzy techniques.
3 Khamooshiand Golafshani(2014) in factuse the abbreviation EDM for
earneddurationmanagement.However,this abbreviationwas already
introduced for the earned duration method of Jacob and Kane (2004). In order
to avoid confusion,we therefore referto earned duration managementby
EDM(t). Furthermore, the suffix (t) also clearly indicates that the technique is
based on time metrics instead of cost metrics.
2 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003

AT represents the actual time (at the current tracking period),
PD the planned duration of the project according to the baseline
schedule, and ES the earned schedule (i.e. the time at which the
currentprojectprogressshould actually have been achieved
according to the plan).Furthermore,PF expresses the perfor-
mance factorthatis assumed.Vandevoorde and Vanhoucke
(2006) and Vanhoucke (2010a) provide an extensive overview of
the performance factorsthatcan be applied forEVM time
forecasting. Nevertheless, the most commonly used performance
factors — which will also be considered in this study — are 1
(i.e.it is assumed thatfuture schedule performance willbe as
planned) and the ES-based schedule performance index SPI(t)
(i.e. it is assumed that future schedule performance will be equal
to the current schedule performance; SPI(t) = ES/AT). Whereas
the simulation study ofVanhoucke and Vandevoorde (2007)
indicated SPI(t)as the bestperforming performancefactor,
Batselier and Vanhoucke (2015b) showed thatsetting PF = 1
produces the mostaccurate time forecasts forthe considered
real-life project data.
Buildingon this basis,a brief discussionof the three
deterministic state-of-the-artmethods for projectduration fore-
casting can now be provided.
2.1. Integrating rework in ESM (Lipke, 2011)
While Lipke etal. (2009)applied statisticalmethodsto
ESM, Lipke (2011)extendsthe techniqueby taking into
account schedule adherence,which can lead to the occurrence
of rework (Lipke, 2004; Vanhoucke, 2010a). More specifically,
the earned value EV is adjusted to the effective earned value
EV(e) through the formula EV(e) = EV − R where R represents
the rework that can be calculated as:
R ¼ 1−PCn e−m 1−PCð Þ 1−pð Þ EV : ð2Þ
PC is the percentage complete of the project(= EV/BAC,
with BAC the budgetat completion) and P is the so-called
p-factor(Lipke, 2004), which expressesthe degreeof
schedule adherence (i.e.P = 1 indicatesperfectschedule
adherence, P = 0 signifies no schedule adherence at all). The
assessmentof the influence of schedule adherence (i.e.the
p-factor) on EVM time forecasting accuracy has already been
the subjectof a few simulation studies (Vanhoucke,2010a,
2013).
The exponents n and m in Eq.(2) are traditionally setto
1 and 0.5,respectively,yielding a nearly lineardecrease of
the rework fraction (i.e.the percentage ofthe work not
performed according to schedule that has to be redone) as the
percentage complete increases (Lipke,2011).The adapted
EV(e) can then be used to calculate ES(e),and through that,
SPI(t)(e) = ES(e)/AT.The targeted projectduration forecast
can then be obtained by substituting ES by ES(e) and using
SPI(t)(e) as a performance factor in the generic ESM formula
(Eq. (1)). Of course,1 can also be used as a performance
factor here.
2.2. Integrating activity sensitivity in ESM (Elshaer, 2013)
Elaborating on the idea of integrating schedule risk ana
(SRA) and EVM as proposed by Vanhoucke (2010a); Vanh
(2010b);Vanhoucke (2011);Vanhoucke (2012); Elshaer (2013)
suggeststo take into accountactivity sensitivity information
(i.e. SRA) for the calculation ofprojectduration forecasts
(i.e. EVM). More specifically, activity-based sensitivity me
are used as weighing parameters for the PV and EV of the
The rationale is that this would lead to a more accurate s
performance by removing or decreasing the negative effe
warning signals caused by non-criticalactivities.The criticality
index CI appeared to yield the best results as a weighing
(Elshaer,2013).Therefore,this activity sensitivity measure —
which can be calculated by performing Monte Carlo simu
based on the activity duration distribution profiles (i.e. tri
distributions which can be either symmetrical or skewed
or to the right, depending on the characteristics of the ac
will be applied here.Moreover,since weighing PV and EV
results in an adjusted ES and SPI(t), the EAC(t) will also c
(see Eq. (1)), both with PF = 1 and PF = SPI(t).
2.3.Calculating schedule performance in time units: EDM
(Khamooshi and Golafshani, 2014)
Khamooshi and Golafshani (2014) argue that time fore
ing with ESM could still yield misleading resultsas the
technique keeps using costs as a proxy to measure sched
performance(i.e. ES is calculated based on EV and PV
values,which are both expressed in costunits).Therefore,
they developed the technique of earned duration manage
or EDM(t),in which schedule and cost performance measu
are completely decoupled.More specifically,the ES metric is
replaced by earned duration ED(t),which is calculated as the
projection of the total earned duration TED (i.e. the sum
earned durations of all the in-progress and completed ac
at AT4) on the total planned duration TPD (i.e.the sum of the
planned durations of all the planned activities at AT acco
to the baseline schedule) instead of the projection of EV
which yields ES. Besides the fact that the calculation of E
based on metrics that are expressed in time units (i.e. TE
TPD) instead of costunits (i.e.EV and PV),it is completely
similar to the calculation of ES. To obtain time forecasts f
the EDM(t) methodology, we apply following formula5:
EAC tð Þ ¼PD
DPI : ð3Þ
This formula is strongly parallelto thatof the traditional
PVM (i.e. PVM-SPI: EAC(t) = PD/SPI),butwith the perfor-
mance factor changed to the duration performance index
4 The earned duration of an in-progress (or completed) activity at AT is
planned baseline duration of thatactivity multiplied by the actualpercentage
complete (or physical progress) of that activity at AT.
5 Khamooshi and Golafshani (2014) actually use the notation EDAC for
estimated duration (or time) atcompletion,which is substantially exactly the
same as EAC(t).
3J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
PD the planned duration of the project according to the baseline
schedule, and ES the earned schedule (i.e. the time at which the
currentprojectprogressshould actually have been achieved
according to the plan).Furthermore,PF expresses the perfor-
mance factorthatis assumed.Vandevoorde and Vanhoucke
(2006) and Vanhoucke (2010a) provide an extensive overview of
the performance factorsthatcan be applied forEVM time
forecasting. Nevertheless, the most commonly used performance
factors — which will also be considered in this study — are 1
(i.e.it is assumed thatfuture schedule performance willbe as
planned) and the ES-based schedule performance index SPI(t)
(i.e. it is assumed that future schedule performance will be equal
to the current schedule performance; SPI(t) = ES/AT). Whereas
the simulation study ofVanhoucke and Vandevoorde (2007)
indicated SPI(t)as the bestperforming performancefactor,
Batselier and Vanhoucke (2015b) showed thatsetting PF = 1
produces the mostaccurate time forecasts forthe considered
real-life project data.
Buildingon this basis,a brief discussionof the three
deterministic state-of-the-artmethods for projectduration fore-
casting can now be provided.
2.1. Integrating rework in ESM (Lipke, 2011)
While Lipke etal. (2009)applied statisticalmethodsto
ESM, Lipke (2011)extendsthe techniqueby taking into
account schedule adherence,which can lead to the occurrence
of rework (Lipke, 2004; Vanhoucke, 2010a). More specifically,
the earned value EV is adjusted to the effective earned value
EV(e) through the formula EV(e) = EV − R where R represents
the rework that can be calculated as:
R ¼ 1−PCn e−m 1−PCð Þ 1−pð Þ EV : ð2Þ
PC is the percentage complete of the project(= EV/BAC,
with BAC the budgetat completion) and P is the so-called
p-factor(Lipke, 2004), which expressesthe degreeof
schedule adherence (i.e.P = 1 indicatesperfectschedule
adherence, P = 0 signifies no schedule adherence at all). The
assessmentof the influence of schedule adherence (i.e.the
p-factor) on EVM time forecasting accuracy has already been
the subjectof a few simulation studies (Vanhoucke,2010a,
2013).
The exponents n and m in Eq.(2) are traditionally setto
1 and 0.5,respectively,yielding a nearly lineardecrease of
the rework fraction (i.e.the percentage ofthe work not
performed according to schedule that has to be redone) as the
percentage complete increases (Lipke,2011).The adapted
EV(e) can then be used to calculate ES(e),and through that,
SPI(t)(e) = ES(e)/AT.The targeted projectduration forecast
can then be obtained by substituting ES by ES(e) and using
SPI(t)(e) as a performance factor in the generic ESM formula
(Eq. (1)). Of course,1 can also be used as a performance
factor here.
2.2. Integrating activity sensitivity in ESM (Elshaer, 2013)
Elaborating on the idea of integrating schedule risk ana
(SRA) and EVM as proposed by Vanhoucke (2010a); Vanh
(2010b);Vanhoucke (2011);Vanhoucke (2012); Elshaer (2013)
suggeststo take into accountactivity sensitivity information
(i.e. SRA) for the calculation ofprojectduration forecasts
(i.e. EVM). More specifically, activity-based sensitivity me
are used as weighing parameters for the PV and EV of the
The rationale is that this would lead to a more accurate s
performance by removing or decreasing the negative effe
warning signals caused by non-criticalactivities.The criticality
index CI appeared to yield the best results as a weighing
(Elshaer,2013).Therefore,this activity sensitivity measure —
which can be calculated by performing Monte Carlo simu
based on the activity duration distribution profiles (i.e. tri
distributions which can be either symmetrical or skewed
or to the right, depending on the characteristics of the ac
will be applied here.Moreover,since weighing PV and EV
results in an adjusted ES and SPI(t), the EAC(t) will also c
(see Eq. (1)), both with PF = 1 and PF = SPI(t).
2.3.Calculating schedule performance in time units: EDM
(Khamooshi and Golafshani, 2014)
Khamooshi and Golafshani (2014) argue that time fore
ing with ESM could still yield misleading resultsas the
technique keeps using costs as a proxy to measure sched
performance(i.e. ES is calculated based on EV and PV
values,which are both expressed in costunits).Therefore,
they developed the technique of earned duration manage
or EDM(t),in which schedule and cost performance measu
are completely decoupled.More specifically,the ES metric is
replaced by earned duration ED(t),which is calculated as the
projection of the total earned duration TED (i.e. the sum
earned durations of all the in-progress and completed ac
at AT4) on the total planned duration TPD (i.e.the sum of the
planned durations of all the planned activities at AT acco
to the baseline schedule) instead of the projection of EV
which yields ES. Besides the fact that the calculation of E
based on metrics that are expressed in time units (i.e. TE
TPD) instead of costunits (i.e.EV and PV),it is completely
similar to the calculation of ES. To obtain time forecasts f
the EDM(t) methodology, we apply following formula5:
EAC tð Þ ¼PD
DPI : ð3Þ
This formula is strongly parallelto thatof the traditional
PVM (i.e. PVM-SPI: EAC(t) = PD/SPI),butwith the perfor-
mance factor changed to the duration performance index
4 The earned duration of an in-progress (or completed) activity at AT is
planned baseline duration of thatactivity multiplied by the actualpercentage
complete (or physical progress) of that activity at AT.
5 Khamooshi and Golafshani (2014) actually use the notation EDAC for
estimated duration (or time) atcompletion,which is substantially exactly the
same as EAC(t).
3J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
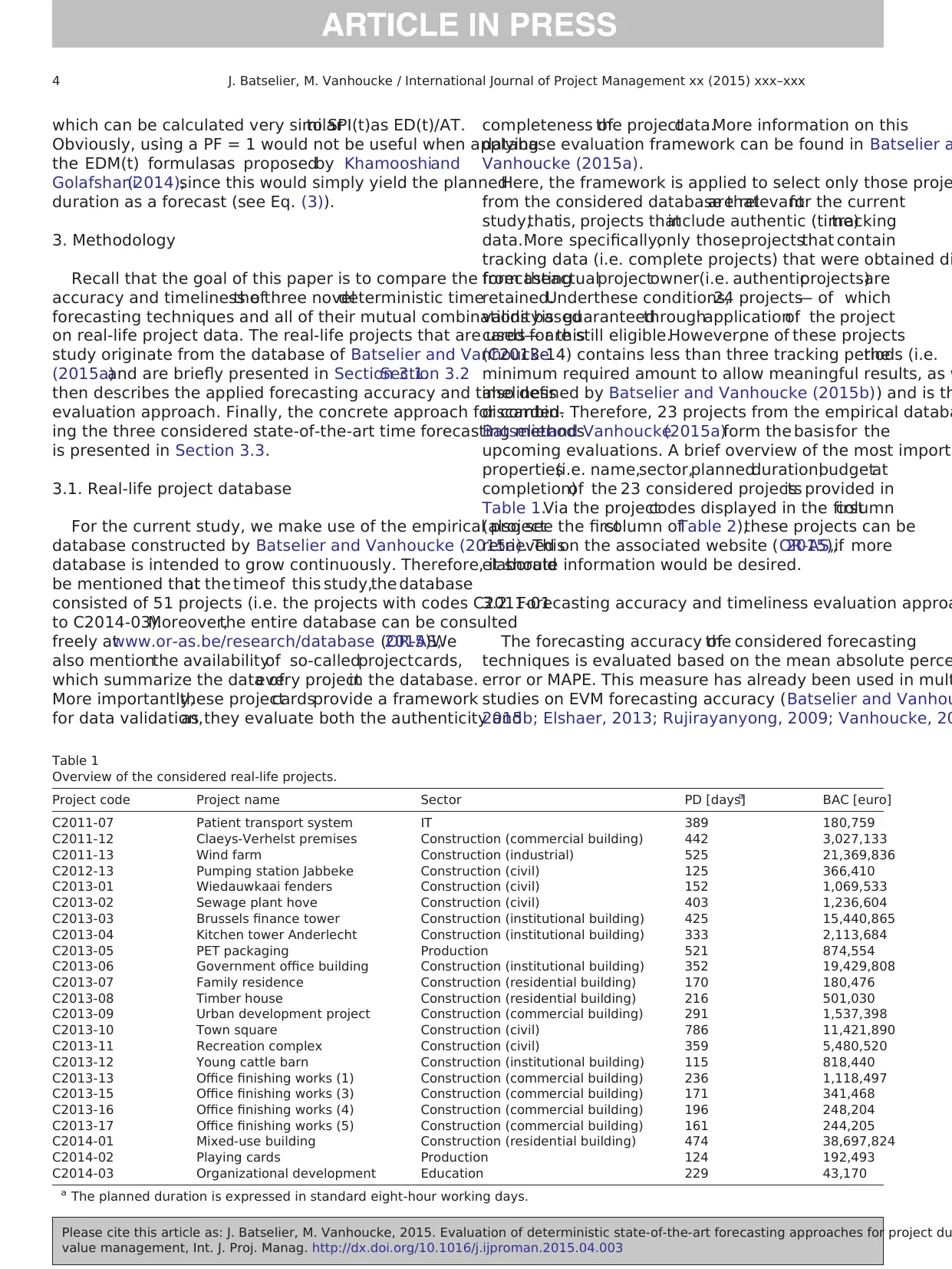
which can be calculated very similarto SPI(t)as ED(t)/AT.
Obviously, using a PF = 1 would not be useful when applying
the EDM(t) formulasas proposedby Khamooshiand
Golafshani(2014),since this would simply yield the planned
duration as a forecast (see Eq. (3)).
3. Methodology
Recall that the goal of this paper is to compare the forecasting
accuracy and timeliness ofthe three noveldeterministic time
forecasting techniques and all of their mutual combinations based
on real-life project data. The real-life projects that are used for this
study originate from the database of Batselier and Vanhoucke
(2015a)and are briefly presented in Section 3.1.Section 3.2
then describes the applied forecasting accuracy and timeliness
evaluation approach. Finally, the concrete approach for combin-
ing the three considered state-of-the-art time forecasting methods
is presented in Section 3.3.
3.1. Real-life project database
For the current study, we make use of the empirical project
database constructed by Batselier and Vanhoucke (2015a). This
database is intended to grow continuously. Therefore, it should
be mentioned thatat the timeof this study,the database
consisted of 51 projects (i.e. the projects with codes C2011-01
to C2014-03).Moreover,the entire database can be consulted
freely atwww.or-as.be/research/database (OR-AS,2015).We
also mentionthe availabilityof so-calledprojectcards,
which summarize the data ofevery projectin the database.
More importantly,these projectcardsprovide a framework
for data validation,as they evaluate both the authenticity and
completeness ofthe projectdata.More information on this
database evaluation framework can be found in Batselier a
Vanhoucke (2015a).
Here, the framework is applied to select only those proje
from the considered database thatare relevantfor the current
study,thatis, projects thatinclude authentic (time)tracking
data.More specifically,only thoseprojectsthat contain
tracking data (i.e. complete projects) that were obtained di
from theactualprojectowner(i.e. authenticprojects)are
retained.Underthese conditions,24 projects— of which
validityis guaranteedthroughapplicationof the project
cards— are still eligible.However,one of these projects
(C2013-14) contains less than three tracking periods (i.e.the
minimum required amount to allow meaningful results, as w
also defined by Batselier and Vanhoucke (2015b)) and is th
discarded. Therefore, 23 projects from the empirical databa
Batselierand Vanhoucke(2015a)form the basisfor the
upcoming evaluations. A brief overview of the most importa
properties(i.e. name,sector,plannedduration,budgetat
completion)of the 23 considered projectsis provided in
Table 1.Via the projectcodes displayed in the firstcolumn
(also see the firstcolumn ofTable 2),these projects can be
retrieved on the associated website (OR-AS,2015),if more
elaborate information would be desired.
3.2. Forecasting accuracy and timeliness evaluation approa
The forecasting accuracy ofthe considered forecasting
techniques is evaluated based on the mean absolute perce
error or MAPE. This measure has already been used in mult
studies on EVM forecasting accuracy (Batselier and Vanhou
2015b; Elshaer, 2013; Rujirayanyong, 2009; Vanhoucke, 20
Table 1
Overview of the considered real-life projects.
Project code Project name Sector PD [days]a BAC [euro]
C2011-07 Patient transport system IT 389 180,759
C2011-12 Claeys-Verhelst premises Construction (commercial building) 442 3,027,133
C2011-13 Wind farm Construction (industrial) 525 21,369,836
C2012-13 Pumping station Jabbeke Construction (civil) 125 366,410
C2013-01 Wiedauwkaai fenders Construction (civil) 152 1,069,533
C2013-02 Sewage plant hove Construction (civil) 403 1,236,604
C2013-03 Brussels finance tower Construction (institutional building) 425 15,440,865
C2013-04 Kitchen tower Anderlecht Construction (institutional building) 333 2,113,684
C2013-05 PET packaging Production 521 874,554
C2013-06 Government office building Construction (institutional building) 352 19,429,808
C2013-07 Family residence Construction (residential building) 170 180,476
C2013-08 Timber house Construction (residential building) 216 501,030
C2013-09 Urban development project Construction (commercial building) 291 1,537,398
C2013-10 Town square Construction (civil) 786 11,421,890
C2013-11 Recreation complex Construction (civil) 359 5,480,520
C2013-12 Young cattle barn Construction (institutional building) 115 818,440
C2013-13 Office finishing works (1) Construction (commercial building) 236 1,118,497
C2013-15 Office finishing works (3) Construction (commercial building) 171 341,468
C2013-16 Office finishing works (4) Construction (commercial building) 196 248,204
C2013-17 Office finishing works (5) Construction (commercial building) 161 244,205
C2014-01 Mixed-use building Construction (residential building) 474 38,697,824
C2014-02 Playing cards Production 124 192,493
C2014-03 Organizational development Education 229 43,170
a The planned duration is expressed in standard eight-hour working days.
4 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Obviously, using a PF = 1 would not be useful when applying
the EDM(t) formulasas proposedby Khamooshiand
Golafshani(2014),since this would simply yield the planned
duration as a forecast (see Eq. (3)).
3. Methodology
Recall that the goal of this paper is to compare the forecasting
accuracy and timeliness ofthe three noveldeterministic time
forecasting techniques and all of their mutual combinations based
on real-life project data. The real-life projects that are used for this
study originate from the database of Batselier and Vanhoucke
(2015a)and are briefly presented in Section 3.1.Section 3.2
then describes the applied forecasting accuracy and timeliness
evaluation approach. Finally, the concrete approach for combin-
ing the three considered state-of-the-art time forecasting methods
is presented in Section 3.3.
3.1. Real-life project database
For the current study, we make use of the empirical project
database constructed by Batselier and Vanhoucke (2015a). This
database is intended to grow continuously. Therefore, it should
be mentioned thatat the timeof this study,the database
consisted of 51 projects (i.e. the projects with codes C2011-01
to C2014-03).Moreover,the entire database can be consulted
freely atwww.or-as.be/research/database (OR-AS,2015).We
also mentionthe availabilityof so-calledprojectcards,
which summarize the data ofevery projectin the database.
More importantly,these projectcardsprovide a framework
for data validation,as they evaluate both the authenticity and
completeness ofthe projectdata.More information on this
database evaluation framework can be found in Batselier a
Vanhoucke (2015a).
Here, the framework is applied to select only those proje
from the considered database thatare relevantfor the current
study,thatis, projects thatinclude authentic (time)tracking
data.More specifically,only thoseprojectsthat contain
tracking data (i.e. complete projects) that were obtained di
from theactualprojectowner(i.e. authenticprojects)are
retained.Underthese conditions,24 projects— of which
validityis guaranteedthroughapplicationof the project
cards— are still eligible.However,one of these projects
(C2013-14) contains less than three tracking periods (i.e.the
minimum required amount to allow meaningful results, as w
also defined by Batselier and Vanhoucke (2015b)) and is th
discarded. Therefore, 23 projects from the empirical databa
Batselierand Vanhoucke(2015a)form the basisfor the
upcoming evaluations. A brief overview of the most importa
properties(i.e. name,sector,plannedduration,budgetat
completion)of the 23 considered projectsis provided in
Table 1.Via the projectcodes displayed in the firstcolumn
(also see the firstcolumn ofTable 2),these projects can be
retrieved on the associated website (OR-AS,2015),if more
elaborate information would be desired.
3.2. Forecasting accuracy and timeliness evaluation approa
The forecasting accuracy ofthe considered forecasting
techniques is evaluated based on the mean absolute perce
error or MAPE. This measure has already been used in mult
studies on EVM forecasting accuracy (Batselier and Vanhou
2015b; Elshaer, 2013; Rujirayanyong, 2009; Vanhoucke, 20
Table 1
Overview of the considered real-life projects.
Project code Project name Sector PD [days]a BAC [euro]
C2011-07 Patient transport system IT 389 180,759
C2011-12 Claeys-Verhelst premises Construction (commercial building) 442 3,027,133
C2011-13 Wind farm Construction (industrial) 525 21,369,836
C2012-13 Pumping station Jabbeke Construction (civil) 125 366,410
C2013-01 Wiedauwkaai fenders Construction (civil) 152 1,069,533
C2013-02 Sewage plant hove Construction (civil) 403 1,236,604
C2013-03 Brussels finance tower Construction (institutional building) 425 15,440,865
C2013-04 Kitchen tower Anderlecht Construction (institutional building) 333 2,113,684
C2013-05 PET packaging Production 521 874,554
C2013-06 Government office building Construction (institutional building) 352 19,429,808
C2013-07 Family residence Construction (residential building) 170 180,476
C2013-08 Timber house Construction (residential building) 216 501,030
C2013-09 Urban development project Construction (commercial building) 291 1,537,398
C2013-10 Town square Construction (civil) 786 11,421,890
C2013-11 Recreation complex Construction (civil) 359 5,480,520
C2013-12 Young cattle barn Construction (institutional building) 115 818,440
C2013-13 Office finishing works (1) Construction (commercial building) 236 1,118,497
C2013-15 Office finishing works (3) Construction (commercial building) 171 341,468
C2013-16 Office finishing works (4) Construction (commercial building) 196 248,204
C2013-17 Office finishing works (5) Construction (commercial building) 161 244,205
C2014-01 Mixed-use building Construction (residential building) 474 38,697,824
C2014-02 Playing cards Production 124 192,493
C2014-03 Organizational development Education 229 43,170
a The planned duration is expressed in standard eight-hour working days.
4 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
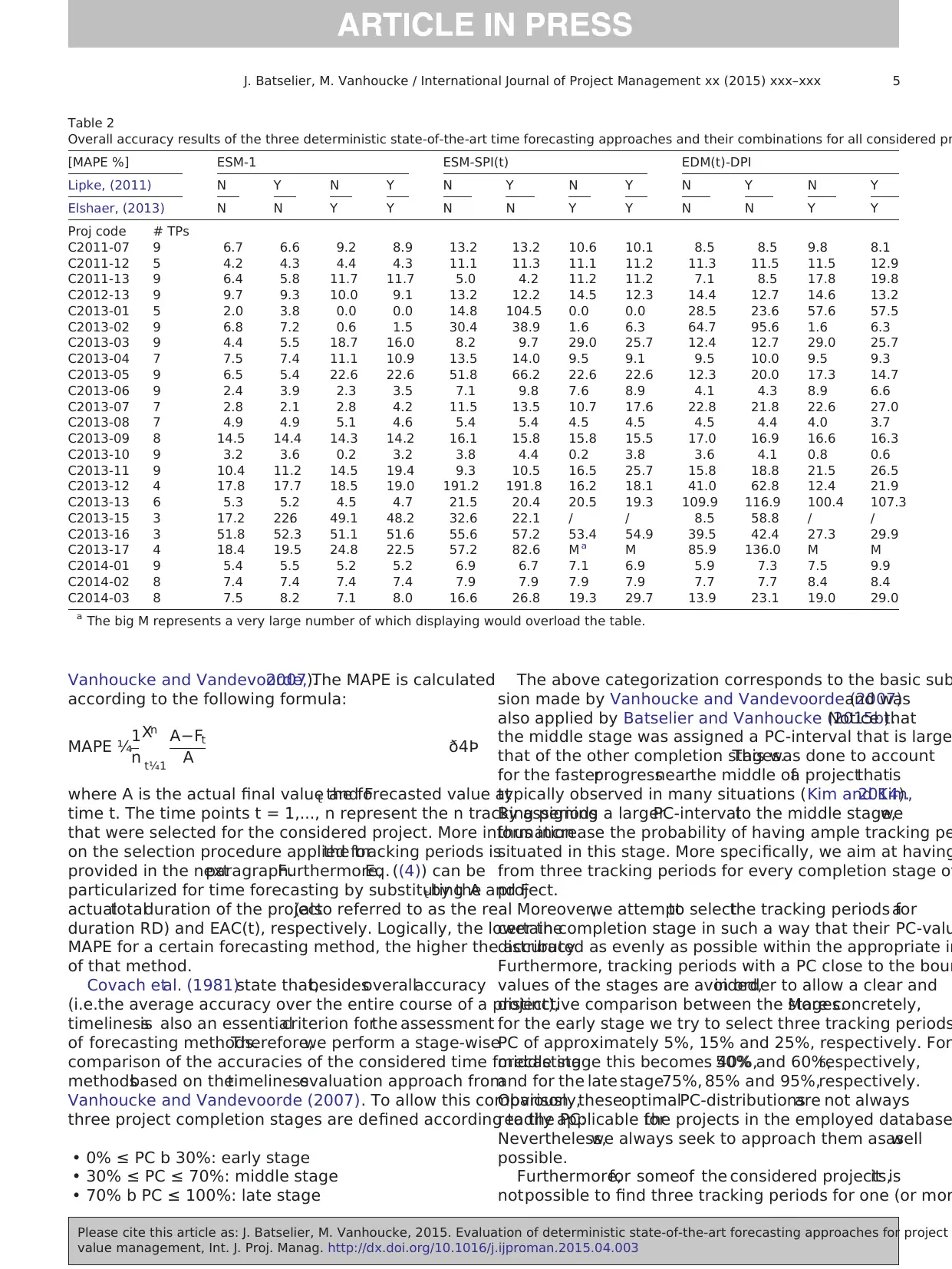
Vanhoucke and Vandevoorde,2007).The MAPE is calculated
according to the following formula:
MAPE ¼1
n
Xn
t¼1
A−Ft
A ð4Þ
where A is the actual final value and Ft the forecasted value at
time t. The time points t = 1,..., n represent the n tracking periods
that were selected for the considered project. More information
on the selection procedure applied forthe tracking periods is
provided in the nextparagraph.Furthermore,Eq. ((4)) can be
particularized for time forecasting by substituting A and Ft by the
actualtotalduration of the project(also referred to as the real
duration RD) and EAC(t), respectively. Logically, the lower the
MAPE for a certain forecasting method, the higher the accuracy
of that method.
Covach etal. (1981)state that,besidesoverallaccuracy
(i.e.the average accuracy over the entire course of a project),
timelinessis also an essentialcriterion forthe assessment
of forecasting methods.Therefore,we perform a stage-wise
comparison of the accuracies of the considered time forecasting
methodsbased on thetimelinessevaluation approach from
Vanhoucke and Vandevoorde (2007). To allow this comparison,
three project completion stages are defined according to the PC:
• 0% ≤ PC b 30%: early stage
• 30% ≤ PC ≤ 70%: middle stage
• 70% b PC ≤ 100%: late stage
The above categorization corresponds to the basic sub
sion made by Vanhoucke and Vandevoorde (2007)and was
also applied by Batselier and Vanhoucke (2015b).Notice that
the middle stage was assigned a PC-interval that is large
that of the other completion stages.This was done to account
for the fasterprogressnearthe middle ofa projectthatis
typically observed in many situations (Kim and Kim,2014).
By assigning a largerPC-intervalto the middle stage,we
thus increase the probability of having ample tracking pe
situated in this stage. More specifically, we aim at having
from three tracking periods for every completion stage of
project.
Moreover,we attemptto selectthe tracking periods fora
certain completion stage in such a way that their PC-valu
distributed as evenly as possible within the appropriate in
Furthermore, tracking periods with a PC close to the boun
values of the stages are avoided,in order to allow a clear and
distinctive comparison between the stages.More concretely,
for the early stage we try to select three tracking periods
PC of approximately 5%, 15% and 25%, respectively. For
middle stage this becomes 40%,50% and 60%,respectively,
and for the late stage75%, 85% and 95%,respectively.
Obviously,theseoptimalPC-distributionsare not always
readily applicable forthe projects in the employed database
Nevertheless,we always seek to approach them as wellas
possible.
Furthermore,for someof the considered projects,it is
notpossible to find three tracking periods for one (or mor
Table 2
Overall accuracy results of the three deterministic state-of-the-art time forecasting approaches and their combinations for all considered pr
[MAPE %] ESM-1 ESM-SPI(t) EDM(t)-DPI
Lipke, (2011) N Y N Y N Y N Y N Y N Y
Elshaer, (2013) N N Y Y N N Y Y N N Y Y
Proj code # TPs
C2011-07 9 6.7 6.6 9.2 8.9 13.2 13.2 10.6 10.1 8.5 8.5 9.8 8.1
C2011-12 5 4.2 4.3 4.4 4.3 11.1 11.3 11.1 11.2 11.3 11.5 11.5 12.9
C2011-13 9 6.4 5.8 11.7 11.7 5.0 4.2 11.2 11.2 7.1 8.5 17.8 19.8
C2012-13 9 9.7 9.3 10.0 9.1 13.2 12.2 14.5 12.3 14.4 12.7 14.6 13.2
C2013-01 5 2.0 3.8 0.0 0.0 14.8 104.5 0.0 0.0 28.5 23.6 57.6 57.5
C2013-02 9 6.8 7.2 0.6 1.5 30.4 38.9 1.6 6.3 64.7 95.6 1.6 6.3
C2013-03 9 4.4 5.5 18.7 16.0 8.2 9.7 29.0 25.7 12.4 12.7 29.0 25.7
C2013-04 7 7.5 7.4 11.1 10.9 13.5 14.0 9.5 9.1 9.5 10.0 9.5 9.3
C2013-05 9 6.5 5.4 22.6 22.6 51.8 66.2 22.6 22.6 12.3 20.0 17.3 14.7
C2013-06 9 2.4 3.9 2.3 3.5 7.1 9.8 7.6 8.9 4.1 4.3 8.9 6.6
C2013-07 7 2.8 2.1 2.8 4.2 11.5 13.5 10.7 17.6 22.8 21.8 22.6 27.0
C2013-08 7 4.9 4.9 5.1 4.6 5.4 5.4 4.5 4.5 4.5 4.4 4.0 3.7
C2013-09 8 14.5 14.4 14.3 14.2 16.1 15.8 15.8 15.5 17.0 16.9 16.6 16.3
C2013-10 9 3.2 3.6 0.2 3.2 3.8 4.4 0.2 3.8 3.6 4.1 0.8 0.6
C2013-11 9 10.4 11.2 14.5 19.4 9.3 10.5 16.5 25.7 15.8 18.8 21.5 26.5
C2013-12 4 17.8 17.7 18.5 19.0 191.2 191.8 16.2 18.1 41.0 62.8 12.4 21.9
C2013-13 6 5.3 5.2 4.5 4.7 21.5 20.4 20.5 19.3 109.9 116.9 100.4 107.3
C2013-15 3 17.2 22.6 49.1 48.2 32.6 22.1 / / 8.5 58.8 / /
C2013-16 3 51.8 52.3 51.1 51.6 55.6 57.2 53.4 54.9 39.5 42.4 27.3 29.9
C2013-17 4 18.4 19.5 24.8 22.5 57.2 82.6 M a M 85.9 136.0 M M
C2014-01 9 5.4 5.5 5.2 5.2 6.9 6.7 7.1 6.9 5.9 7.3 7.5 9.9
C2014-02 8 7.4 7.4 7.4 7.4 7.9 7.9 7.9 7.9 7.7 7.7 8.4 8.4
C2014-03 8 7.5 8.2 7.1 8.0 16.6 26.8 19.3 29.7 13.9 23.1 19.0 29.0
a The big M represents a very large number of which displaying would overload the table.
5J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
according to the following formula:
MAPE ¼1
n
Xn
t¼1
A−Ft
A ð4Þ
where A is the actual final value and Ft the forecasted value at
time t. The time points t = 1,..., n represent the n tracking periods
that were selected for the considered project. More information
on the selection procedure applied forthe tracking periods is
provided in the nextparagraph.Furthermore,Eq. ((4)) can be
particularized for time forecasting by substituting A and Ft by the
actualtotalduration of the project(also referred to as the real
duration RD) and EAC(t), respectively. Logically, the lower the
MAPE for a certain forecasting method, the higher the accuracy
of that method.
Covach etal. (1981)state that,besidesoverallaccuracy
(i.e.the average accuracy over the entire course of a project),
timelinessis also an essentialcriterion forthe assessment
of forecasting methods.Therefore,we perform a stage-wise
comparison of the accuracies of the considered time forecasting
methodsbased on thetimelinessevaluation approach from
Vanhoucke and Vandevoorde (2007). To allow this comparison,
three project completion stages are defined according to the PC:
• 0% ≤ PC b 30%: early stage
• 30% ≤ PC ≤ 70%: middle stage
• 70% b PC ≤ 100%: late stage
The above categorization corresponds to the basic sub
sion made by Vanhoucke and Vandevoorde (2007)and was
also applied by Batselier and Vanhoucke (2015b).Notice that
the middle stage was assigned a PC-interval that is large
that of the other completion stages.This was done to account
for the fasterprogressnearthe middle ofa projectthatis
typically observed in many situations (Kim and Kim,2014).
By assigning a largerPC-intervalto the middle stage,we
thus increase the probability of having ample tracking pe
situated in this stage. More specifically, we aim at having
from three tracking periods for every completion stage of
project.
Moreover,we attemptto selectthe tracking periods fora
certain completion stage in such a way that their PC-valu
distributed as evenly as possible within the appropriate in
Furthermore, tracking periods with a PC close to the boun
values of the stages are avoided,in order to allow a clear and
distinctive comparison between the stages.More concretely,
for the early stage we try to select three tracking periods
PC of approximately 5%, 15% and 25%, respectively. For
middle stage this becomes 40%,50% and 60%,respectively,
and for the late stage75%, 85% and 95%,respectively.
Obviously,theseoptimalPC-distributionsare not always
readily applicable forthe projects in the employed database
Nevertheless,we always seek to approach them as wellas
possible.
Furthermore,for someof the considered projects,it is
notpossible to find three tracking periods for one (or mor
Table 2
Overall accuracy results of the three deterministic state-of-the-art time forecasting approaches and their combinations for all considered pr
[MAPE %] ESM-1 ESM-SPI(t) EDM(t)-DPI
Lipke, (2011) N Y N Y N Y N Y N Y N Y
Elshaer, (2013) N N Y Y N N Y Y N N Y Y
Proj code # TPs
C2011-07 9 6.7 6.6 9.2 8.9 13.2 13.2 10.6 10.1 8.5 8.5 9.8 8.1
C2011-12 5 4.2 4.3 4.4 4.3 11.1 11.3 11.1 11.2 11.3 11.5 11.5 12.9
C2011-13 9 6.4 5.8 11.7 11.7 5.0 4.2 11.2 11.2 7.1 8.5 17.8 19.8
C2012-13 9 9.7 9.3 10.0 9.1 13.2 12.2 14.5 12.3 14.4 12.7 14.6 13.2
C2013-01 5 2.0 3.8 0.0 0.0 14.8 104.5 0.0 0.0 28.5 23.6 57.6 57.5
C2013-02 9 6.8 7.2 0.6 1.5 30.4 38.9 1.6 6.3 64.7 95.6 1.6 6.3
C2013-03 9 4.4 5.5 18.7 16.0 8.2 9.7 29.0 25.7 12.4 12.7 29.0 25.7
C2013-04 7 7.5 7.4 11.1 10.9 13.5 14.0 9.5 9.1 9.5 10.0 9.5 9.3
C2013-05 9 6.5 5.4 22.6 22.6 51.8 66.2 22.6 22.6 12.3 20.0 17.3 14.7
C2013-06 9 2.4 3.9 2.3 3.5 7.1 9.8 7.6 8.9 4.1 4.3 8.9 6.6
C2013-07 7 2.8 2.1 2.8 4.2 11.5 13.5 10.7 17.6 22.8 21.8 22.6 27.0
C2013-08 7 4.9 4.9 5.1 4.6 5.4 5.4 4.5 4.5 4.5 4.4 4.0 3.7
C2013-09 8 14.5 14.4 14.3 14.2 16.1 15.8 15.8 15.5 17.0 16.9 16.6 16.3
C2013-10 9 3.2 3.6 0.2 3.2 3.8 4.4 0.2 3.8 3.6 4.1 0.8 0.6
C2013-11 9 10.4 11.2 14.5 19.4 9.3 10.5 16.5 25.7 15.8 18.8 21.5 26.5
C2013-12 4 17.8 17.7 18.5 19.0 191.2 191.8 16.2 18.1 41.0 62.8 12.4 21.9
C2013-13 6 5.3 5.2 4.5 4.7 21.5 20.4 20.5 19.3 109.9 116.9 100.4 107.3
C2013-15 3 17.2 22.6 49.1 48.2 32.6 22.1 / / 8.5 58.8 / /
C2013-16 3 51.8 52.3 51.1 51.6 55.6 57.2 53.4 54.9 39.5 42.4 27.3 29.9
C2013-17 4 18.4 19.5 24.8 22.5 57.2 82.6 M a M 85.9 136.0 M M
C2014-01 9 5.4 5.5 5.2 5.2 6.9 6.7 7.1 6.9 5.9 7.3 7.5 9.9
C2014-02 8 7.4 7.4 7.4 7.4 7.9 7.9 7.9 7.9 7.7 7.7 8.4 8.4
C2014-03 8 7.5 8.2 7.1 8.0 16.6 26.8 19.3 29.7 13.9 23.1 19.0 29.0
a The big M represents a very large number of which displaying would overload the table.
5J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003

completion stages,regardless ofthe optimalPC-distribution.
For these projects,the totalnumberof considered tracking
periods— needed for the overall forecastingaccuracy
evaluation — will thus be lower than nine (i.e. worse than the
bestcasesituation ofthreetracking periodsfor all three
completion stages), which can be seen from the second column
of Table 2.Moreover,we already mention that no results will
be taken into account for a certain stage of a project if it does
not contain the desired amount of three tracking periods.
3.3.Combination of the three state-of-the-art time forecasting
methods
Notice thatthe methodsproposed by Lipke (2011)and
Elshaer (2013) are in factextensions of the traditionalESM.
This is also indicated by the expression of the basic principle
of the methods,namely “integration ofactivity sensitivity
in ESM” and “integration ofactivity sensitivity in ESM”,
respectively. Indeed, both methods still produce forecasts based
on the generic formula (Eq.(1)).Khamooshiand Golafshani
(2014),on the otherhand,actually developed an approach
sprouting from ESM but with a different definition of the key
metrics (i.e. time-based instead of cost-based). Therefore, ESM
and EDM(t)can be seen as two separate methodologies for
obtaining projectduration forecastsand can thusboth be
used in combination with the approaches of Lipke (2011) and
Elshaer(2013).The implementation ofthe two extending
techniques— in what follows sometimesreferredto as
“extensions” — is completely similar for EDM(t) as for ESM
(see explanation in Sections 2.1 and 2.2).Also note thatthe
techniques of Lipke (2011) and Elshaer (2013) cannot only be
applied separately, but also combined.
Furthermore, since both the performance factors 1 and SPI(t)
are relevantfor ESM — whereas only PF = DPI is usefulin
the currentEDM(t) formulas — there is a totalof 12 time
forecasting variations to be evaluated, as appears from Table 2.
Notice thatthe traditionalESM-1 and ESM-SPI(t) are indeed
used as a benchmark,as they respectively correspond to the
third and seventh column of Table 2, where neither of the two
extensions are applied to ESM. This is indicated by the two Ns
(“No”) in the second and third row of the table. Oppositely, a Y
(“Yes”) in one of these rows signifies thatthe corresponding
technique is indeed applied.
4. Results and discussion
The overall accuracy results (i.e. the average accuracy over
the entire course of a project, so over all tracking periods of all
stages) of the three deterministic state-of-the-art time forecast-
ing approaches and their combinations are shown in Table 2,
for all 23 considered projects of the database ofBatselier and
Vanhoucke (2015a).However,the results forsome projects
(marked in italicsin Table 2) are notrelevantfor overall
accuracy evaluation due to various reasons,which are now
listed.
For projects C2013-01, C2013-12 and C2013-17, the results
for the firsttracking period (ata PC of 3%, 6% and 8%,
respectively)are too sensitive to variations in EV and ED(t)
because of the low levels of PV and TPD atthese very early
completion stages.Therefore,the overallresultsfor these
projects also become biased (with MAPEs of over 100%),as
they include the outcomesof the firsttracking period.For
projectC2013-15,the method of Elshaer (2013) could notbe
applied to ESM-SPI(t) and EDM(t)-DPI. More specifically, for
the first two tracking periods(at a PC of 4% and 22%,
respectively),the activities with a CI N 0 had notstarted yet,
yielding an ES and ED(t)equalto zero and thereforean
SPI(t) = DPI = 0.If these performance factors are inserted in
Eqs.(1) and (3),respectively,it indeed appears thatEAC(t)
cannotbe calculated (division by zero)and thusno time
forecasts can be obtained. Therefore, just as projects C201
C2013-12 and C2013-17, project C2013-15 is discarded for
overall evaluation of the forecasting accuracy of the consid
methods.Note,however,thatfor allfour projects the biasing
results only occur in the early stage (i.e.PC b 30%).Hence,
these projects can still be considered for accuracy evaluati
the middle and late stages.
ProjectC2013-13 displays biasing results for EDM(t)-DPI
due to the existence of a very expensive activity (about 85
the BAC) with a duration that is strongly disproportionate to
high cost.In such situations,EDM(t)-DPI thus appears to be
less appropriate for forecasting project duration.Nevertheless,
this situationis ratherexceptional,and therefore,project
C2013-13 is discarded for all stages to allow a fair comparis
between EDM(t)-DPIand the ESM techniques.A total of
five projectsare thus discardedfor the overalaccuracy
evaluationof the threedeterministicstate-of-the-arttime
forecasting approaches and their combinations. The summ
overallresults (i.e.overthe entire projectcourse)for the 18
retained projects are shown on the first row of MAPE-outco
of Table 3 and are now discussed.
It clearly appears thatESM-1 provides the bestbasis for
making accurate time forecasts over allstages of the project.
The ESM-1 withoutextensions shows the lowestMAPE of
9.0% and thus dominates both ESM-SPI(t) and EDM(t)-DPI,
which attain amaximum accuracy of14.1% and13.8%
MAPE, respectively,both with application ofthe method of
Elshaer(2013).These outcomes are notentirely unexpected,
as Batselierand Vanhoucke(2015b)alreadyindicated
thatfor ESM a PF = 1 yields more accurate forecasts than
a PF = SPI(t).By extension,it could thusbe stated that
unweighted time forecasting methods (i.e.future performance
is assumed to be as planned)outdo theirperformance-based
counterparts (i.e. future performance is assumed to be equ
the current performance), which also include EDM(t)-DPI. T
main reason forthe supremacy ofunweighted forecasting
methods — such as ESM-1 here — is that they implicitly tak
into accountpotentialcorrective actions performed by man-
agementin orderto improvelagging projectperformance.
The effectsof thesemanagementactionsare obviously
comprised in the real-life projectdata.Therefore,the current
(poor) performance expressed by the SPI(t) or DPIdoes not
adequately reflectthe actualfutureperformance,which is
subject to the corrective actions.
6 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
For these projects,the totalnumberof considered tracking
periods— needed for the overall forecastingaccuracy
evaluation — will thus be lower than nine (i.e. worse than the
bestcasesituation ofthreetracking periodsfor all three
completion stages), which can be seen from the second column
of Table 2.Moreover,we already mention that no results will
be taken into account for a certain stage of a project if it does
not contain the desired amount of three tracking periods.
3.3.Combination of the three state-of-the-art time forecasting
methods
Notice thatthe methodsproposed by Lipke (2011)and
Elshaer (2013) are in factextensions of the traditionalESM.
This is also indicated by the expression of the basic principle
of the methods,namely “integration ofactivity sensitivity
in ESM” and “integration ofactivity sensitivity in ESM”,
respectively. Indeed, both methods still produce forecasts based
on the generic formula (Eq.(1)).Khamooshiand Golafshani
(2014),on the otherhand,actually developed an approach
sprouting from ESM but with a different definition of the key
metrics (i.e. time-based instead of cost-based). Therefore, ESM
and EDM(t)can be seen as two separate methodologies for
obtaining projectduration forecastsand can thusboth be
used in combination with the approaches of Lipke (2011) and
Elshaer(2013).The implementation ofthe two extending
techniques— in what follows sometimesreferredto as
“extensions” — is completely similar for EDM(t) as for ESM
(see explanation in Sections 2.1 and 2.2).Also note thatthe
techniques of Lipke (2011) and Elshaer (2013) cannot only be
applied separately, but also combined.
Furthermore, since both the performance factors 1 and SPI(t)
are relevantfor ESM — whereas only PF = DPI is usefulin
the currentEDM(t) formulas — there is a totalof 12 time
forecasting variations to be evaluated, as appears from Table 2.
Notice thatthe traditionalESM-1 and ESM-SPI(t) are indeed
used as a benchmark,as they respectively correspond to the
third and seventh column of Table 2, where neither of the two
extensions are applied to ESM. This is indicated by the two Ns
(“No”) in the second and third row of the table. Oppositely, a Y
(“Yes”) in one of these rows signifies thatthe corresponding
technique is indeed applied.
4. Results and discussion
The overall accuracy results (i.e. the average accuracy over
the entire course of a project, so over all tracking periods of all
stages) of the three deterministic state-of-the-art time forecast-
ing approaches and their combinations are shown in Table 2,
for all 23 considered projects of the database ofBatselier and
Vanhoucke (2015a).However,the results forsome projects
(marked in italicsin Table 2) are notrelevantfor overall
accuracy evaluation due to various reasons,which are now
listed.
For projects C2013-01, C2013-12 and C2013-17, the results
for the firsttracking period (ata PC of 3%, 6% and 8%,
respectively)are too sensitive to variations in EV and ED(t)
because of the low levels of PV and TPD atthese very early
completion stages.Therefore,the overallresultsfor these
projects also become biased (with MAPEs of over 100%),as
they include the outcomesof the firsttracking period.For
projectC2013-15,the method of Elshaer (2013) could notbe
applied to ESM-SPI(t) and EDM(t)-DPI. More specifically, for
the first two tracking periods(at a PC of 4% and 22%,
respectively),the activities with a CI N 0 had notstarted yet,
yielding an ES and ED(t)equalto zero and thereforean
SPI(t) = DPI = 0.If these performance factors are inserted in
Eqs.(1) and (3),respectively,it indeed appears thatEAC(t)
cannotbe calculated (division by zero)and thusno time
forecasts can be obtained. Therefore, just as projects C201
C2013-12 and C2013-17, project C2013-15 is discarded for
overall evaluation of the forecasting accuracy of the consid
methods.Note,however,thatfor allfour projects the biasing
results only occur in the early stage (i.e.PC b 30%).Hence,
these projects can still be considered for accuracy evaluati
the middle and late stages.
ProjectC2013-13 displays biasing results for EDM(t)-DPI
due to the existence of a very expensive activity (about 85
the BAC) with a duration that is strongly disproportionate to
high cost.In such situations,EDM(t)-DPI thus appears to be
less appropriate for forecasting project duration.Nevertheless,
this situationis ratherexceptional,and therefore,project
C2013-13 is discarded for all stages to allow a fair comparis
between EDM(t)-DPIand the ESM techniques.A total of
five projectsare thus discardedfor the overalaccuracy
evaluationof the threedeterministicstate-of-the-arttime
forecasting approaches and their combinations. The summ
overallresults (i.e.overthe entire projectcourse)for the 18
retained projects are shown on the first row of MAPE-outco
of Table 3 and are now discussed.
It clearly appears thatESM-1 provides the bestbasis for
making accurate time forecasts over allstages of the project.
The ESM-1 withoutextensions shows the lowestMAPE of
9.0% and thus dominates both ESM-SPI(t) and EDM(t)-DPI,
which attain amaximum accuracy of14.1% and13.8%
MAPE, respectively,both with application ofthe method of
Elshaer(2013).These outcomes are notentirely unexpected,
as Batselierand Vanhoucke(2015b)alreadyindicated
thatfor ESM a PF = 1 yields more accurate forecasts than
a PF = SPI(t).By extension,it could thusbe stated that
unweighted time forecasting methods (i.e.future performance
is assumed to be as planned)outdo theirperformance-based
counterparts (i.e. future performance is assumed to be equ
the current performance), which also include EDM(t)-DPI. T
main reason forthe supremacy ofunweighted forecasting
methods — such as ESM-1 here — is that they implicitly tak
into accountpotentialcorrective actions performed by man-
agementin orderto improvelagging projectperformance.
The effectsof thesemanagementactionsare obviously
comprised in the real-life projectdata.Therefore,the current
(poor) performance expressed by the SPI(t) or DPIdoes not
adequately reflectthe actualfutureperformance,which is
subject to the corrective actions.
6 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
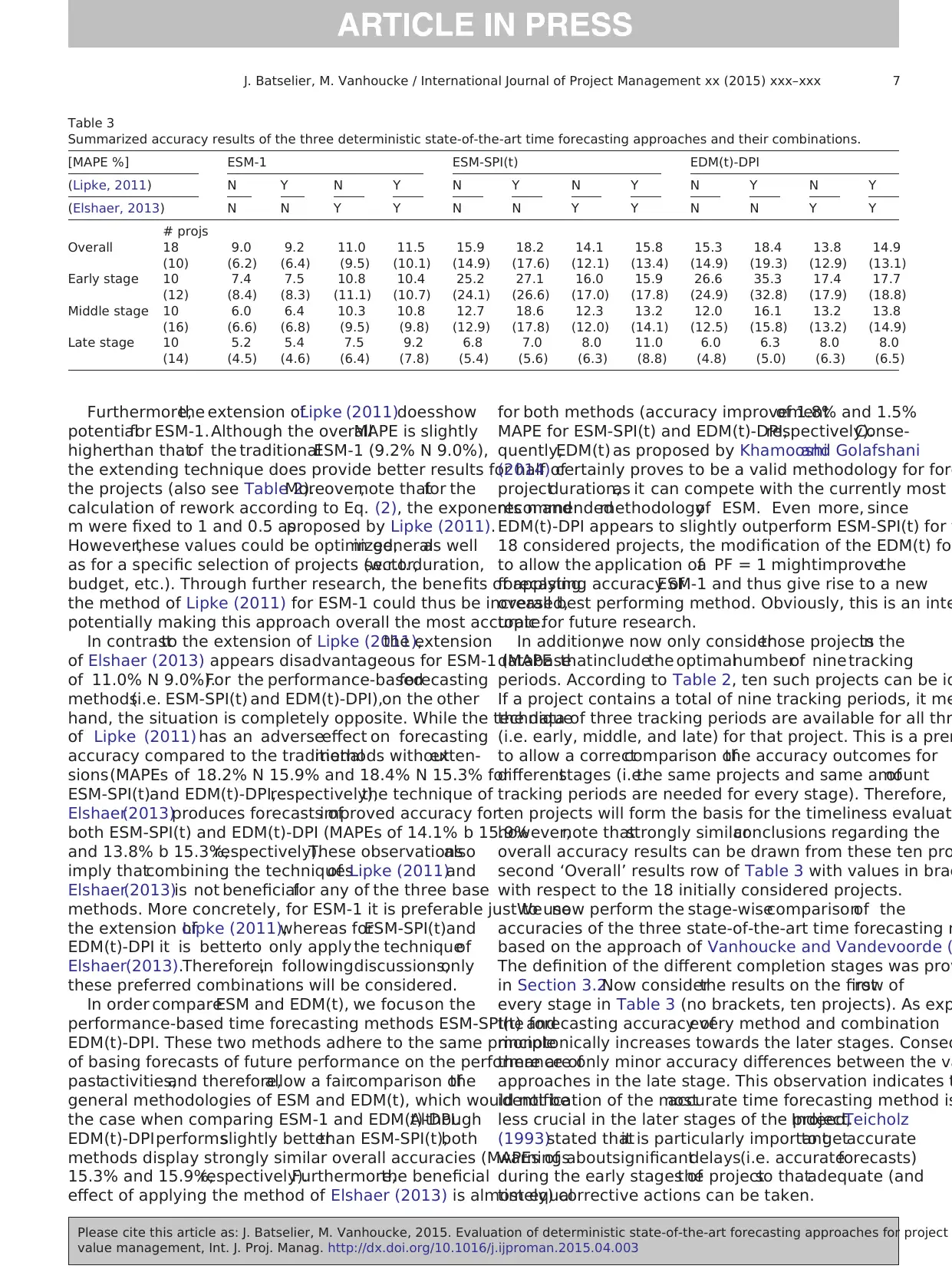
Furthermore,the extension ofLipke (2011)doesshow
potentialfor ESM-1.Although the overallMAPE is slightly
higherthan thatof the traditionalESM-1 (9.2% N 9.0%),
the extending technique does provide better results for half of
the projects (also see Table 2).Moreover,note thatfor the
calculation of rework according to Eq. (2), the exponents n and
m were fixed to 1 and 0.5 asproposed by Lipke (2011).
However,these values could be optimized,in generalas well
as for a specific selection of projects (w.r.t.sector,duration,
budget, etc.). Through further research, the benefits of applying
the method of Lipke (2011) for ESM-1 could thus be increased,
potentially making this approach overall the most accurate.
In contrastto the extension of Lipke (2011),the extension
of Elshaer (2013) appears disadvantageous for ESM-1 (MAPE
of 11.0% N 9.0%).For the performance-basedforecasting
methods(i.e. ESM-SPI(t) and EDM(t)-DPI),on the other
hand, the situation is completely opposite. While the technique
of Lipke (2011) has an adverseeffect on forecasting
accuracy compared to the traditionalmethods withoutexten-
sions(MAPEs of 18.2% N 15.9% and 18.4% N 15.3% for
ESM-SPI(t)and EDM(t)-DPI,respectively),the technique of
Elshaer(2013)produces forecasts ofimproved accuracy for
both ESM-SPI(t) and EDM(t)-DPI (MAPEs of 14.1% b 15.9%
and 13.8% b 15.3%,respectively).These observationsalso
imply thatcombining the techniquesof Lipke (2011)and
Elshaer(2013)is not beneficialfor any of the three base
methods. More concretely, for ESM-1 it is preferable just to use
the extension ofLipke (2011),whereas forESM-SPI(t)and
EDM(t)-DPI it is betterto only apply the techniqueof
Elshaer(2013).Therefore,in followingdiscussions,only
these preferred combinations will be considered.
In order compareESM and EDM(t), we focuson the
performance-based time forecasting methods ESM-SPI(t) and
EDM(t)-DPI. These two methods adhere to the same principle
of basing forecasts of future performance on the performance of
pastactivities,and therefore,allow a faircomparison ofthe
general methodologies of ESM and EDM(t), which would not be
the case when comparing ESM-1 and EDM(t)-DPI.Although
EDM(t)-DPIperformsslightly betterthan ESM-SPI(t),both
methods display strongly similar overall accuracies (MAPEs of
15.3% and 15.9%,respectively).Furthermore,the beneficial
effect of applying the method of Elshaer (2013) is almost equal
for both methods (accuracy improvementof 1.8% and 1.5%
MAPE for ESM-SPI(t) and EDM(t)-DPI,respectively).Conse-
quently,EDM(t) as proposed by Khamooshiand Golafshani
(2014) certainly proves to be a valid methodology for fore
projectduration,as it can compete with the currently most
recommendedmethodologyof ESM. Even more, since
EDM(t)-DPI appears to slightly outperform ESM-SPI(t) for t
18 considered projects, the modification of the EDM(t) fo
to allow the application ofa PF = 1 mightimprovethe
forecasting accuracy ofESM-1 and thus give rise to a new
overall best performing method. Obviously, this is an inte
topic for future research.
In addition,we now only considerthose projectsin the
databasethatincludethe optimalnumberof nine tracking
periods. According to Table 2, ten such projects can be id
If a project contains a total of nine tracking periods, it me
the data of three tracking periods are available for all thr
(i.e. early, middle, and late) for that project. This is a prer
to allow a correctcomparison ofthe accuracy outcomes for
differentstages (i.e.the same projects and same amountof
tracking periods are needed for every stage). Therefore,
ten projects will form the basis for the timeliness evaluat
however,note thatstrongly similarconclusions regarding the
overall accuracy results can be drawn from these ten pro
second ‘Overall’ results row of Table 3 with values in brac
with respect to the 18 initially considered projects.
We now perform the stage-wisecomparisonof the
accuracies of the three state-of-the-art time forecasting m
based on the approach of Vanhoucke and Vandevoorde (
The definition of the different completion stages was prov
in Section 3.2.Now considerthe results on the firstrow of
every stage in Table 3 (no brackets, ten projects). As exp
the forecasting accuracy ofevery method and combination
monotonically increases towards the later stages. Conseq
there are only minor accuracy differences between the va
approaches in the late stage. This observation indicates t
identification of the mostaccurate time forecasting method is
less crucial in the later stages of the project.Indeed,Teicholz
(1993)stated thatit is particularly importantto getaccurate
warningsaboutsignificantdelays(i.e. accurateforecasts)
during the early stages ofthe projectso thatadequate (and
timely) corrective actions can be taken.
Table 3
Summarized accuracy results of the three deterministic state-of-the-art time forecasting approaches and their combinations.
[MAPE %] ESM-1 ESM-SPI(t) EDM(t)-DPI
(Lipke, 2011) N Y N Y N Y N Y N Y N Y
(Elshaer, 2013) N N Y Y N N Y Y N N Y Y
# projs
Overall 18 9.0 9.2 11.0 11.5 15.9 18.2 14.1 15.8 15.3 18.4 13.8 14.9
(10) (6.2) (6.4) (9.5) (10.1) (14.9) (17.6) (12.1) (13.4) (14.9) (19.3) (12.9) (13.1)
Early stage 10 7.4 7.5 10.8 10.4 25.2 27.1 16.0 15.9 26.6 35.3 17.4 17.7
(12) (8.4) (8.3) (11.1) (10.7) (24.1) (26.6) (17.0) (17.8) (24.9) (32.8) (17.9) (18.8)
Middle stage 10 6.0 6.4 10.3 10.8 12.7 18.6 12.3 13.2 12.0 16.1 13.2 13.8
(16) (6.6) (6.8) (9.5) (9.8) (12.9) (17.8) (12.0) (14.1) (12.5) (15.8) (13.2) (14.9)
Late stage 10 5.2 5.4 7.5 9.2 6.8 7.0 8.0 11.0 6.0 6.3 8.0 8.0
(14) (4.5) (4.6) (6.4) (7.8) (5.4) (5.6) (6.3) (8.8) (4.8) (5.0) (6.3) (6.5)
7J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
potentialfor ESM-1.Although the overallMAPE is slightly
higherthan thatof the traditionalESM-1 (9.2% N 9.0%),
the extending technique does provide better results for half of
the projects (also see Table 2).Moreover,note thatfor the
calculation of rework according to Eq. (2), the exponents n and
m were fixed to 1 and 0.5 asproposed by Lipke (2011).
However,these values could be optimized,in generalas well
as for a specific selection of projects (w.r.t.sector,duration,
budget, etc.). Through further research, the benefits of applying
the method of Lipke (2011) for ESM-1 could thus be increased,
potentially making this approach overall the most accurate.
In contrastto the extension of Lipke (2011),the extension
of Elshaer (2013) appears disadvantageous for ESM-1 (MAPE
of 11.0% N 9.0%).For the performance-basedforecasting
methods(i.e. ESM-SPI(t) and EDM(t)-DPI),on the other
hand, the situation is completely opposite. While the technique
of Lipke (2011) has an adverseeffect on forecasting
accuracy compared to the traditionalmethods withoutexten-
sions(MAPEs of 18.2% N 15.9% and 18.4% N 15.3% for
ESM-SPI(t)and EDM(t)-DPI,respectively),the technique of
Elshaer(2013)produces forecasts ofimproved accuracy for
both ESM-SPI(t) and EDM(t)-DPI (MAPEs of 14.1% b 15.9%
and 13.8% b 15.3%,respectively).These observationsalso
imply thatcombining the techniquesof Lipke (2011)and
Elshaer(2013)is not beneficialfor any of the three base
methods. More concretely, for ESM-1 it is preferable just to use
the extension ofLipke (2011),whereas forESM-SPI(t)and
EDM(t)-DPI it is betterto only apply the techniqueof
Elshaer(2013).Therefore,in followingdiscussions,only
these preferred combinations will be considered.
In order compareESM and EDM(t), we focuson the
performance-based time forecasting methods ESM-SPI(t) and
EDM(t)-DPI. These two methods adhere to the same principle
of basing forecasts of future performance on the performance of
pastactivities,and therefore,allow a faircomparison ofthe
general methodologies of ESM and EDM(t), which would not be
the case when comparing ESM-1 and EDM(t)-DPI.Although
EDM(t)-DPIperformsslightly betterthan ESM-SPI(t),both
methods display strongly similar overall accuracies (MAPEs of
15.3% and 15.9%,respectively).Furthermore,the beneficial
effect of applying the method of Elshaer (2013) is almost equal
for both methods (accuracy improvementof 1.8% and 1.5%
MAPE for ESM-SPI(t) and EDM(t)-DPI,respectively).Conse-
quently,EDM(t) as proposed by Khamooshiand Golafshani
(2014) certainly proves to be a valid methodology for fore
projectduration,as it can compete with the currently most
recommendedmethodologyof ESM. Even more, since
EDM(t)-DPI appears to slightly outperform ESM-SPI(t) for t
18 considered projects, the modification of the EDM(t) fo
to allow the application ofa PF = 1 mightimprovethe
forecasting accuracy ofESM-1 and thus give rise to a new
overall best performing method. Obviously, this is an inte
topic for future research.
In addition,we now only considerthose projectsin the
databasethatincludethe optimalnumberof nine tracking
periods. According to Table 2, ten such projects can be id
If a project contains a total of nine tracking periods, it me
the data of three tracking periods are available for all thr
(i.e. early, middle, and late) for that project. This is a prer
to allow a correctcomparison ofthe accuracy outcomes for
differentstages (i.e.the same projects and same amountof
tracking periods are needed for every stage). Therefore,
ten projects will form the basis for the timeliness evaluat
however,note thatstrongly similarconclusions regarding the
overall accuracy results can be drawn from these ten pro
second ‘Overall’ results row of Table 3 with values in brac
with respect to the 18 initially considered projects.
We now perform the stage-wisecomparisonof the
accuracies of the three state-of-the-art time forecasting m
based on the approach of Vanhoucke and Vandevoorde (
The definition of the different completion stages was prov
in Section 3.2.Now considerthe results on the firstrow of
every stage in Table 3 (no brackets, ten projects). As exp
the forecasting accuracy ofevery method and combination
monotonically increases towards the later stages. Conseq
there are only minor accuracy differences between the va
approaches in the late stage. This observation indicates t
identification of the mostaccurate time forecasting method is
less crucial in the later stages of the project.Indeed,Teicholz
(1993)stated thatit is particularly importantto getaccurate
warningsaboutsignificantdelays(i.e. accurateforecasts)
during the early stages ofthe projectso thatadequate (and
timely) corrective actions can be taken.
Table 3
Summarized accuracy results of the three deterministic state-of-the-art time forecasting approaches and their combinations.
[MAPE %] ESM-1 ESM-SPI(t) EDM(t)-DPI
(Lipke, 2011) N Y N Y N Y N Y N Y N Y
(Elshaer, 2013) N N Y Y N N Y Y N N Y Y
# projs
Overall 18 9.0 9.2 11.0 11.5 15.9 18.2 14.1 15.8 15.3 18.4 13.8 14.9
(10) (6.2) (6.4) (9.5) (10.1) (14.9) (17.6) (12.1) (13.4) (14.9) (19.3) (12.9) (13.1)
Early stage 10 7.4 7.5 10.8 10.4 25.2 27.1 16.0 15.9 26.6 35.3 17.4 17.7
(12) (8.4) (8.3) (11.1) (10.7) (24.1) (26.6) (17.0) (17.8) (24.9) (32.8) (17.9) (18.8)
Middle stage 10 6.0 6.4 10.3 10.8 12.7 18.6 12.3 13.2 12.0 16.1 13.2 13.8
(16) (6.6) (6.8) (9.5) (9.8) (12.9) (17.8) (12.0) (14.1) (12.5) (15.8) (13.2) (14.9)
Late stage 10 5.2 5.4 7.5 9.2 6.8 7.0 8.0 11.0 6.0 6.3 8.0 8.0
(14) (4.5) (4.6) (6.4) (7.8) (5.4) (5.6) (6.3) (8.8) (4.8) (5.0) (6.3) (6.5)
7J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

We thus focus on the early stage forecasting results. First of
all, the dominanceof ESM-1 withoutextensionsand the
potential of the technique of Lipke (2011) in combination with
ESM-1 still exist. A more remarkable observation, however, is
thatthe application ofthe method ofElshaer(2013)proves
much more beneficial for ESM-SPI(t) and EDM(t)-DPI in the
early stage than over all stages of the project (MAPE reductions
of 9.2% for both methodsinsteadof 1.8% and 1.5%,
respectively).This means that the observed overall benefits of
the extensionof Elshaer (2013) for ESM-SPI(t) and
EDM(t)-DPI are mostly due to the very good performance of
the technique in the early stage.Indeed,the technique even
appearsto have a negative effecton the accuracy ofboth
performance-basedtime forecastingmethodsfor the later
stages.Nevertheless,given the greatimportance ofaccurate
early stage forecasts (Teicholz,1993),the method of Elshaer
(2013) can certainly be deemed relevant.
In orderto expand the setof considered projectsfor the
timeliness evaluation, for every completion stage, we now include
all projects that contain three tracking periods for that specific stage
(condition already mentioned in Section 3.2). This implies that we
can now take into accountmore than ten projects for the three
stages (i.e.12,16 and 14 projects for the early,middle and late
stage, respectively), but that we can no longer use the outcomes to
make comparisons between the stages. Nevertheless, for a certain
stage,the forecasting accuracies ofthe differentmethods and
combinations can still be compared. The corresponding results are
displayed on the second row of every stage in Table 3 (in brackets).
Completely similar conclusions regarding the methods' accuracy
can be drawn with respectto the timeliness results presented
earlier, and this for every completion stage.
5. Conclusions
The goalof this paperwas to compare the forecasting
accuracy and timeliness of three deterministic state-of-the-art
timeforecasting techniquesand theirmutualcombinations
based on real-life project data.The three techniques that were
considered are those proposed by Lipke (2011); Elshaer (2013)
and Khamooshi and Golafshani (2014) and are all based on the
EVM methodology.More specifically,Lipke (2011)and
Elshaer(2013)respectivelyintegratereworkand activity
sensitivity in ESM time forecasting,while Khamooshiand
Golafshani(2014)introduce earned duration managementor
EDM(t), a technique that calculates schedule performance from
time-based instead of cost-based metrics.EDM(t) can thus be
seen asa novelbasemethodology forforecasting project
duration (i.e.an alternative forESM), whereas the methods
of Lipke (2011)and Elshaer(2013)are extensionsof the
base methods (i.e.of ESM, butalso ofEDM(t)).Moreover,
these extensions cannotonly be applied separately,butalso
combined. Furthermore, the real-life project data that were used
for the currentstudy originatefrom theempiricalproject
database ofBatselierand Vanhoucke (2015a),of which 23
projects were retained.
The accuracy ofthe considered forecasting methodsis
assessedbasedon the MAPE. Moreover,timelinessis
evaluated according to the stage-wise comparison approac
Vanhoucke and Vandevoorde (2007). We also mention that
ESM technique is applied with the performance factors 1 an
SPI(t), whereas only PF = DPI is useful for EDM(t) under the
currentdefinitions.When also considering the extensions of
Lipke (2011)and Elshaer(2013)(and theircombination),a
total of 12 time forecasting approaches could be evaluated
From this evaluation,it clearly appearsthat ESM-1
dominatesthe performance-based timeforecasting methods
ESM-SPI(t) and EDM(t)-DPI, both overall (i.e. over the entire
course of the project) and for every specific completion sta
(i.e. early,middle,and late).Furthermore,the extension of
Lipke (2011)doesshow potentialfor ESM-1, whereasthe
techniqueof Elshaer(2013)provesdisadvantageous.In
contrast,for the performance-based methods,the observations
are completely reversed. Here, the method of Lipke (2011)
an adverseeffect on forecastingaccuracy,whereasthe
technique ofElshaer(2013)can produce improved forecasts
with respectto the standard methodswithoutextensions.
However, the positive effect of the extension of Elshaer (20
mainly occurs in the early stage of the project, and not in t
stages. Nevertheless, the method of Elshaer (2013) can ce
be deemed relevant considering the great importance of ac
early stage forecasts (Teicholz, 1993). The above discussio
implies that,for none of the three base methods (i.e.ESM-1,
ESM-SPI(t) and EDM(t)-DPI), it appears beneficial to combin
the techniques of Lipke (2011) and Elshaer (2013).
The performance-based time forecasting methods EDM(t
and ESM-SPI(t) (and not ESM-1) are considered in order to a
a fair comparison of the ESM and EDM(t) methodologies. Th
forecasting accuracy ofthe standard versions(i.e. without
extensions) of ESM-SPI(t) and EDM(t)-DPI is strongly similar
and moreover, the positive influence of the extension of Els
(2013) is almost identical for both methods, both overall an
the important early stages. Consequently, EDM(t) as propo
Khamooshi and Golafshani (2014) certainly proves to be a
methodology for forecasting project duration, as it can com
with — and potentiallyimprove— the currentlymost
recommended methodology of ESM.
Since the overallresultsof our studyshow a slight
advantage of EDM(t)-DPIoverESM-SPI(t),the introduction
of an unweightedEDM(t)-basedmethod(i.e. PF = 1;
EDM(t)-1) might yield a new overall best performing metho
if the forecasting accuracy of ESM-1 can be surpassed. Ano
interesting topic for future research is the optimization of t
approach of Lipke (2011) through fine-tuning of the parame
needed for the calculation of the rework fraction,which were
now setto fixed values proposed by the author.As such,the
benefits of applying the said approach for ESM-1 (and for o
methods, perhaps EDM(t)-1) could be increased.
Acknowledgments
We acknowledge the support provided by the “Nationale
van België” (NBB)(BOF12GOA021)and by the “Bijzonder
Onderzoeksfonds” (BOF)for the projectwith contractnumber
BOF12GOA021.
8 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
all, the dominanceof ESM-1 withoutextensionsand the
potential of the technique of Lipke (2011) in combination with
ESM-1 still exist. A more remarkable observation, however, is
thatthe application ofthe method ofElshaer(2013)proves
much more beneficial for ESM-SPI(t) and EDM(t)-DPI in the
early stage than over all stages of the project (MAPE reductions
of 9.2% for both methodsinsteadof 1.8% and 1.5%,
respectively).This means that the observed overall benefits of
the extensionof Elshaer (2013) for ESM-SPI(t) and
EDM(t)-DPI are mostly due to the very good performance of
the technique in the early stage.Indeed,the technique even
appearsto have a negative effecton the accuracy ofboth
performance-basedtime forecastingmethodsfor the later
stages.Nevertheless,given the greatimportance ofaccurate
early stage forecasts (Teicholz,1993),the method of Elshaer
(2013) can certainly be deemed relevant.
In orderto expand the setof considered projectsfor the
timeliness evaluation, for every completion stage, we now include
all projects that contain three tracking periods for that specific stage
(condition already mentioned in Section 3.2). This implies that we
can now take into accountmore than ten projects for the three
stages (i.e.12,16 and 14 projects for the early,middle and late
stage, respectively), but that we can no longer use the outcomes to
make comparisons between the stages. Nevertheless, for a certain
stage,the forecasting accuracies ofthe differentmethods and
combinations can still be compared. The corresponding results are
displayed on the second row of every stage in Table 3 (in brackets).
Completely similar conclusions regarding the methods' accuracy
can be drawn with respectto the timeliness results presented
earlier, and this for every completion stage.
5. Conclusions
The goalof this paperwas to compare the forecasting
accuracy and timeliness of three deterministic state-of-the-art
timeforecasting techniquesand theirmutualcombinations
based on real-life project data.The three techniques that were
considered are those proposed by Lipke (2011); Elshaer (2013)
and Khamooshi and Golafshani (2014) and are all based on the
EVM methodology.More specifically,Lipke (2011)and
Elshaer(2013)respectivelyintegratereworkand activity
sensitivity in ESM time forecasting,while Khamooshiand
Golafshani(2014)introduce earned duration managementor
EDM(t), a technique that calculates schedule performance from
time-based instead of cost-based metrics.EDM(t) can thus be
seen asa novelbasemethodology forforecasting project
duration (i.e.an alternative forESM), whereas the methods
of Lipke (2011)and Elshaer(2013)are extensionsof the
base methods (i.e.of ESM, butalso ofEDM(t)).Moreover,
these extensions cannotonly be applied separately,butalso
combined. Furthermore, the real-life project data that were used
for the currentstudy originatefrom theempiricalproject
database ofBatselierand Vanhoucke (2015a),of which 23
projects were retained.
The accuracy ofthe considered forecasting methodsis
assessedbasedon the MAPE. Moreover,timelinessis
evaluated according to the stage-wise comparison approac
Vanhoucke and Vandevoorde (2007). We also mention that
ESM technique is applied with the performance factors 1 an
SPI(t), whereas only PF = DPI is useful for EDM(t) under the
currentdefinitions.When also considering the extensions of
Lipke (2011)and Elshaer(2013)(and theircombination),a
total of 12 time forecasting approaches could be evaluated
From this evaluation,it clearly appearsthat ESM-1
dominatesthe performance-based timeforecasting methods
ESM-SPI(t) and EDM(t)-DPI, both overall (i.e. over the entire
course of the project) and for every specific completion sta
(i.e. early,middle,and late).Furthermore,the extension of
Lipke (2011)doesshow potentialfor ESM-1, whereasthe
techniqueof Elshaer(2013)provesdisadvantageous.In
contrast,for the performance-based methods,the observations
are completely reversed. Here, the method of Lipke (2011)
an adverseeffect on forecastingaccuracy,whereasthe
technique ofElshaer(2013)can produce improved forecasts
with respectto the standard methodswithoutextensions.
However, the positive effect of the extension of Elshaer (20
mainly occurs in the early stage of the project, and not in t
stages. Nevertheless, the method of Elshaer (2013) can ce
be deemed relevant considering the great importance of ac
early stage forecasts (Teicholz, 1993). The above discussio
implies that,for none of the three base methods (i.e.ESM-1,
ESM-SPI(t) and EDM(t)-DPI), it appears beneficial to combin
the techniques of Lipke (2011) and Elshaer (2013).
The performance-based time forecasting methods EDM(t
and ESM-SPI(t) (and not ESM-1) are considered in order to a
a fair comparison of the ESM and EDM(t) methodologies. Th
forecasting accuracy ofthe standard versions(i.e. without
extensions) of ESM-SPI(t) and EDM(t)-DPI is strongly similar
and moreover, the positive influence of the extension of Els
(2013) is almost identical for both methods, both overall an
the important early stages. Consequently, EDM(t) as propo
Khamooshi and Golafshani (2014) certainly proves to be a
methodology for forecasting project duration, as it can com
with — and potentiallyimprove— the currentlymost
recommended methodology of ESM.
Since the overallresultsof our studyshow a slight
advantage of EDM(t)-DPIoverESM-SPI(t),the introduction
of an unweightedEDM(t)-basedmethod(i.e. PF = 1;
EDM(t)-1) might yield a new overall best performing metho
if the forecasting accuracy of ESM-1 can be surpassed. Ano
interesting topic for future research is the optimization of t
approach of Lipke (2011) through fine-tuning of the parame
needed for the calculation of the rework fraction,which were
now setto fixed values proposed by the author.As such,the
benefits of applying the said approach for ESM-1 (and for o
methods, perhaps EDM(t)-1) could be increased.
Acknowledgments
We acknowledge the support provided by the “Nationale
van België” (NBB)(BOF12GOA021)and by the “Bijzonder
Onderzoeksfonds” (BOF)for the projectwith contractnumber
BOF12GOA021.
8 J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project du
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003

References
Anbari,F., 2003.Earned value projectmanagementmethod and extensions.
Proj. Manag. J. 34, 12–23.
Barraza,G., Back,E., Mata,F., 2004.Probabilistic forecasting ofproject
performance using stochastic S curves. J. Constr. Eng. Manag. 130, 25–32.
Batselier,J., Vanhoucke,M., 2015a.Construction and evaluation framework
for a real-life project database. Int. J. Proj. Manag. 33, 697–710.
Batselier,J., Vanhoucke,M., 2015b.Empiricalevaluation ofearned value
management forecasting accuracy for time and cost. J. Constr. Eng. Manag.
http://dx.doi.org/10.1061/(ASCE)CO.1943-7862.0001008.
Cheng, M.Y., Peng, H.S., Wu, Y.W., Chen, T.L., 2010. Estimate at completion
for constructionprojectsusing evolutionarysupportvectormachine
inference model. Autom. Constr. 19, 619–629.
Covach, J., Haydon, J., Reither, R., 1981. A Study to Determine Indicators and
Methods to Compute Estimate atCompletion (EAC).ManTech Interna-
tional Corporation, Virginia.
Demeulemeester, E., Vanhoucke, M., Herroelen, W., 2003. RanGen: a random
network generator for activity-on-the-node networks. J. Sched. 6, 17–38.
Elshaer,R., 2013.Impactof sensitivity information on the prediction of
project's duration using earned schedule method.Int.J. Proj.Manag.31,
579–588.
Fleming,Q., Koppelman, J., 2010.Earned Value Project Management. fourth
ed. Project Management Institute, Newtown Square, Pennsylvania.
Jacob, D., Kane, M., 2004. Forecasting schedule completion using earned value
metrics? Revisited. The Measurable News Summer 1, pp. 11–17.
Khamooshi, H., Golafshani, H., 2014. EDM: Earned Duration Management, a
new approach to schedule performance management and measurement. Int.
J. Proj. Manag. 32, 1019–1041.
Kim, B.C., Kim, H.J., 2014. Sensitivity of earned value schedule forecasting to
S-curve patterns. J. Constr. Eng. Manag. 140, 04014023.
Lipke, W., 2003.Scheduleis different.The MeasurableNews Summer,
pp. 31–34.
Lipke,W., 2004.Connecting earned value to the schedule.The Measurable
News Winter 1, pp. 6–16.
Lipke, W., 2011.Schedule adherence and rework.PM World Today 13,
pp. 1–14.
Lipke, W., Zwikael, O., Henderson, K., Anbari, F., 2009. Prediction of project
outcome: the application of statistical methods to earned value management
and earned schedule performance indexes. Int. J. Proj. Manag. 27, 400–407.
Naeni,L., Shadrokh,S., Salehipour,A., 2011.A fuzzy approach to earned
value management. Int. J. Proj. Manag. 29, 764–772.
OR-AS, 2015.Online consultation ofthe real-life projectdatabase and the
corresponding project cards (continuously updated). URL:. http://www
research/database.
Pewdum, W., Rujirayanyong, T., Sooksatra, V., 2009. Forecasting final b
and duration of highway construction projects. Eng. Constr. Archit. M
16, 544–557.
PMI, 2008. A Guide to the Project Management Body of Knowledge (PMB
guide). 3rd Edition. Project Management Institute, Newtown Square,
Rujirayanyong,T., 2009.A comparison ofthree completion date predicting
methods for construction projects. J. Res. Eng. Technol. 6, 305–318.
Teicholz,P., 1993.Forecasting final cost and budget of construction projec
J. Comput. Civ. Eng. 7, 511–529.
Vandevoorde,S., Vanhoucke,M., 2006.A comparison ofdifferentproject
duration forecasting methodsusing earned value metrics.Int. J. Proj.
Manag. 24, 289–302.
Vanhoucke,M., 2010a.Measuring time — improving projectperformance
using earnedvalue management.InternationalSeriesin Operations
Research and Management Science vol. 136. Springer.
Vanhoucke,M., 2010b.Using activity sensitivity and network topology
information to monitor project time performance.OMEGA Int.J. Manag.
Sci. 38, 359–370.
Vanhoucke, M., 2011. On the dynamic use of project performance and s
risk information during projecttracking.OMEGA Int.J. Manag.Sci. 39,
416–426.
Vanhoucke,M., 2012.Measuring theefficiency ofprojectcontrolusing
fictitious and empirical project data. Int. J. Proj. Manag. 30, 252–263.
Vanhoucke, M., 2013. The impact of project schedule adherence and re
the duration forecast accuracy of earned value metrics. In: Hoffmann
(Ed.), ProjectManagement:Practices,Challengesand Developments.
NOVA Publishers, pp. 95–131.
Vanhoucke, M., 2014. Integrated project management and control: first
the theory, then the practice. Management for Professionals. Springe
Vanhoucke, M., Vandevoorde, S., 2007. A simulation and evaluation of e
value metricsto forecastthe projectduration.J. Oper.Res. Soc. 58,
1361–1374.
Vanhoucke,M., Coelho,J., Debels,D., Maenhout,B., Tavares,L., 2008.An
evaluation of the adequacy of projectnetwork generators with systemati-
cally sampled networks. Eur. J. Oper. Res. 187, 511–524.
Wauters,M., Vanhoucke,M., 2014.Supportvectormachine regression for
project control forecasting. Autom. Constr. 47, 92–106.
Willems,L., Vanhoucke,M., 2015.Classification of articles and journals on
project control and earned value management (under submission).
9J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
Anbari,F., 2003.Earned value projectmanagementmethod and extensions.
Proj. Manag. J. 34, 12–23.
Barraza,G., Back,E., Mata,F., 2004.Probabilistic forecasting ofproject
performance using stochastic S curves. J. Constr. Eng. Manag. 130, 25–32.
Batselier,J., Vanhoucke,M., 2015a.Construction and evaluation framework
for a real-life project database. Int. J. Proj. Manag. 33, 697–710.
Batselier,J., Vanhoucke,M., 2015b.Empiricalevaluation ofearned value
management forecasting accuracy for time and cost. J. Constr. Eng. Manag.
http://dx.doi.org/10.1061/(ASCE)CO.1943-7862.0001008.
Cheng, M.Y., Peng, H.S., Wu, Y.W., Chen, T.L., 2010. Estimate at completion
for constructionprojectsusing evolutionarysupportvectormachine
inference model. Autom. Constr. 19, 619–629.
Covach, J., Haydon, J., Reither, R., 1981. A Study to Determine Indicators and
Methods to Compute Estimate atCompletion (EAC).ManTech Interna-
tional Corporation, Virginia.
Demeulemeester, E., Vanhoucke, M., Herroelen, W., 2003. RanGen: a random
network generator for activity-on-the-node networks. J. Sched. 6, 17–38.
Elshaer,R., 2013.Impactof sensitivity information on the prediction of
project's duration using earned schedule method.Int.J. Proj.Manag.31,
579–588.
Fleming,Q., Koppelman, J., 2010.Earned Value Project Management. fourth
ed. Project Management Institute, Newtown Square, Pennsylvania.
Jacob, D., Kane, M., 2004. Forecasting schedule completion using earned value
metrics? Revisited. The Measurable News Summer 1, pp. 11–17.
Khamooshi, H., Golafshani, H., 2014. EDM: Earned Duration Management, a
new approach to schedule performance management and measurement. Int.
J. Proj. Manag. 32, 1019–1041.
Kim, B.C., Kim, H.J., 2014. Sensitivity of earned value schedule forecasting to
S-curve patterns. J. Constr. Eng. Manag. 140, 04014023.
Lipke, W., 2003.Scheduleis different.The MeasurableNews Summer,
pp. 31–34.
Lipke,W., 2004.Connecting earned value to the schedule.The Measurable
News Winter 1, pp. 6–16.
Lipke, W., 2011.Schedule adherence and rework.PM World Today 13,
pp. 1–14.
Lipke, W., Zwikael, O., Henderson, K., Anbari, F., 2009. Prediction of project
outcome: the application of statistical methods to earned value management
and earned schedule performance indexes. Int. J. Proj. Manag. 27, 400–407.
Naeni,L., Shadrokh,S., Salehipour,A., 2011.A fuzzy approach to earned
value management. Int. J. Proj. Manag. 29, 764–772.
OR-AS, 2015.Online consultation ofthe real-life projectdatabase and the
corresponding project cards (continuously updated). URL:. http://www
research/database.
Pewdum, W., Rujirayanyong, T., Sooksatra, V., 2009. Forecasting final b
and duration of highway construction projects. Eng. Constr. Archit. M
16, 544–557.
PMI, 2008. A Guide to the Project Management Body of Knowledge (PMB
guide). 3rd Edition. Project Management Institute, Newtown Square,
Rujirayanyong,T., 2009.A comparison ofthree completion date predicting
methods for construction projects. J. Res. Eng. Technol. 6, 305–318.
Teicholz,P., 1993.Forecasting final cost and budget of construction projec
J. Comput. Civ. Eng. 7, 511–529.
Vandevoorde,S., Vanhoucke,M., 2006.A comparison ofdifferentproject
duration forecasting methodsusing earned value metrics.Int. J. Proj.
Manag. 24, 289–302.
Vanhoucke,M., 2010a.Measuring time — improving projectperformance
using earnedvalue management.InternationalSeriesin Operations
Research and Management Science vol. 136. Springer.
Vanhoucke,M., 2010b.Using activity sensitivity and network topology
information to monitor project time performance.OMEGA Int.J. Manag.
Sci. 38, 359–370.
Vanhoucke, M., 2011. On the dynamic use of project performance and s
risk information during projecttracking.OMEGA Int.J. Manag.Sci. 39,
416–426.
Vanhoucke,M., 2012.Measuring theefficiency ofprojectcontrolusing
fictitious and empirical project data. Int. J. Proj. Manag. 30, 252–263.
Vanhoucke, M., 2013. The impact of project schedule adherence and re
the duration forecast accuracy of earned value metrics. In: Hoffmann
(Ed.), ProjectManagement:Practices,Challengesand Developments.
NOVA Publishers, pp. 95–131.
Vanhoucke, M., 2014. Integrated project management and control: first
the theory, then the practice. Management for Professionals. Springe
Vanhoucke, M., Vandevoorde, S., 2007. A simulation and evaluation of e
value metricsto forecastthe projectduration.J. Oper.Res. Soc. 58,
1361–1374.
Vanhoucke,M., Coelho,J., Debels,D., Maenhout,B., Tavares,L., 2008.An
evaluation of the adequacy of projectnetwork generators with systemati-
cally sampled networks. Eur. J. Oper. Res. 187, 511–524.
Wauters,M., Vanhoucke,M., 2014.Supportvectormachine regression for
project control forecasting. Autom. Constr. 47, 92–106.
Willems,L., Vanhoucke,M., 2015.Classification of articles and journals on
project control and earned value management (under submission).
9J. Batselier, M. Vanhoucke / International Journal of Project Management xx (2015) xxx–xxx
Please cite this article as: J. Batselier, M. Vanhoucke, 2015. Evaluation of deterministic state-of-the-art forecasting approaches for project
value management, Int. J. Proj. Manag. http://dx.doi.org/10.1016/j.ijproman.2015.04.003
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
