Physics Homework: Coulomb's Law, Lens Formula, and Force Analysis

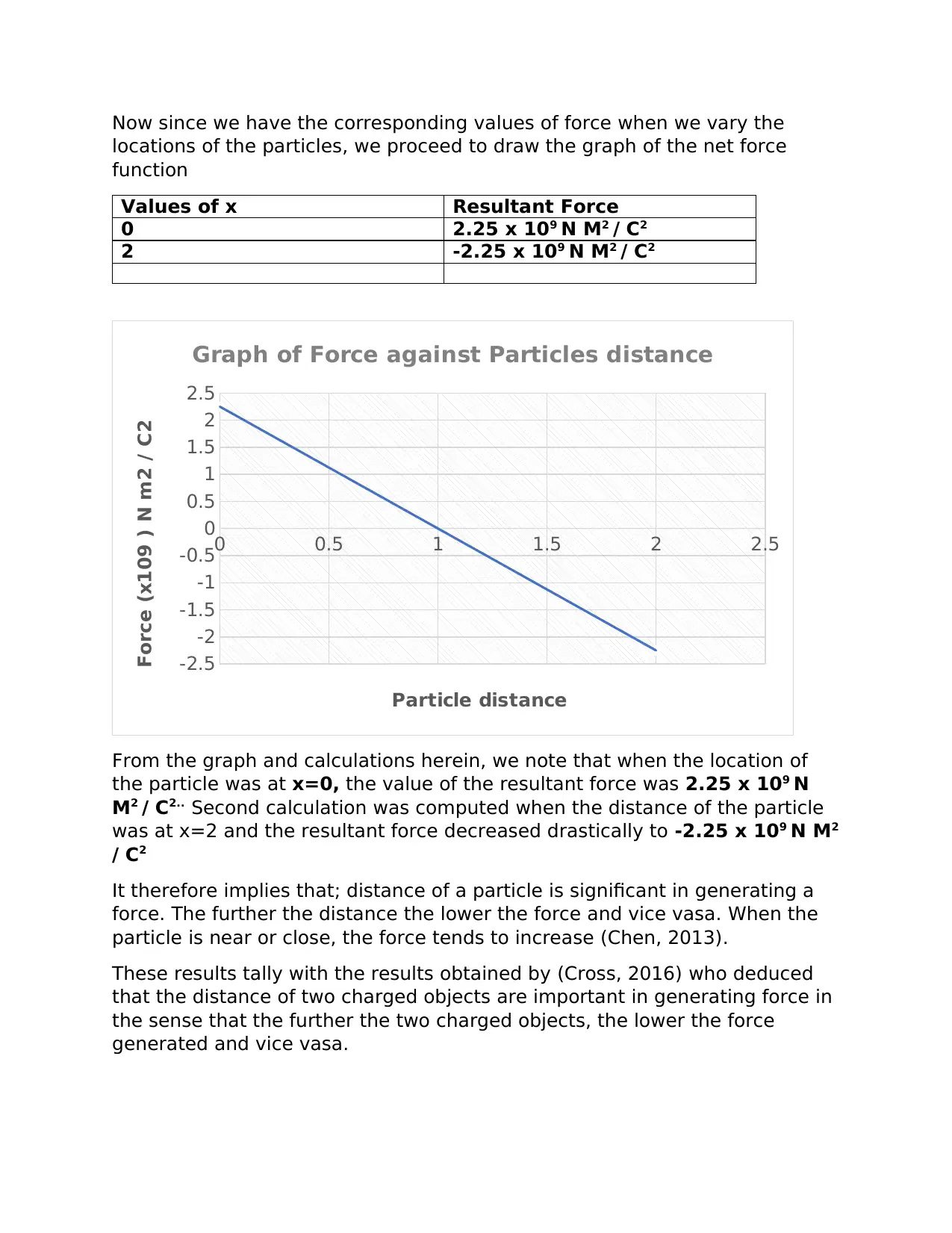
This physics assignment provides solutions to two problems. The first problem focuses on calculating the resultant force based on Coulomb's law, considering variations in the distance between charged particles. The solution includes calculations for different particle locations and a graphical representation of the force. The assignment highlights the relationship between distance and force, with references to supporting research. The second problem addresses the lens formula, deriving a formula for the distance between an object and its image. The solution manipulates the lens formula to find an expression for 'u' associated with the minimum distance between object and image. The assignment demonstrates problem-solving skills in physics, using formulas and calculations to analyze physical phenomena.

SOLUTION
QUESTION THREE (3)
K is a positive constant normally known as coulombs constant and which is
approximated to be 9 x 109 N M2 / C2 as defined by (Schmidt, 2020)
K ~ 9 x 109 N M2 / C2
Based on the formula given,
F = ((-K/X2) + (K/X-2)2)
Where F is the force
K is the coulombs constant
X is the location of the particles
We have been given two locations of the particles x =0 and x =2
We are therefore expected to calculate the force when there is variation of
the distance of the particles between x=0 and x=2
Values of x Resultant Force
When x is 0 Force is 2.25 x 109 N M2 / C2
When x is 2 Force is -2.25 x 109 N M2 / C2
Now we compute the values of Force using the formula
When x is 0
F = ((-K/X2) + (K/X-2)2)
F = ((-9 x 109 N M2 /C2) / 02) + ((9 x 109 N M2 / C2) / (0-2)2)
F= 0 + (9 x 109 N M2 / C2) / 4
F= (9 x 109 N M2 / C2) / 4
F= 2.25 x 109 N M2 / C2
When x is 2
F = ((-K/X2) + (K/X-2)2)
F = ((-9 x 109 N M2 /C2) / 22) + ((9 x 109 N M2 / C2) / (2-2)2)
F= (-9 x 109 N M2 / C2) / 4 + 0
F= (-9 x 109 N M2 / C2) / 4
F= -2.25 x 109 N M2 / C2

Now since we have the corresponding values of force when we vary the
locations of the particles, we proceed to draw the graph of the net force
function
Values of x Resultant Force
0 2.25 x 109 N M2 / C2
2 -2.25 x 109 N M2 / C2
0 0.5 1 1.5 2 2.5
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
Graph of Force against Particles distance
Particle distance
Force (x109 ) N m2 / C2
From the graph and calculations herein, we note that when the location of
the particle was at x=0, the value of the resultant force was 2.25 x 109 N
M2 / C2.. Second calculation was computed when the distance of the particle
was at x=2 and the resultant force decreased drastically to -2.25 x 109 N M2
/ C2
It therefore implies that; distance of a particle is significant in generating a
force. The further the distance the lower the force and vice vasa. When the
particle is near or close, the force tends to increase (Chen, 2013).
These results tally with the results obtained by (Cross, 2016) who deduced
that the distance of two charged objects are important in generating force in
the sense that the further the two charged objects, the lower the force
generated and vice vasa.

QUESTION TWENTY (20)
(a)
The lens formula is a standard formula used globally (A. N. Alexandrov,
2010)
The formula is therefore written as follows
1/f = 1/u + 1/v
We are interested with the distance between the object and the image which
in this case is u+v
1/f =v+u/uv
Uv*1/f=uv*(v+u)/uv
Uv/f = v+u
(b)
From the equation calculated in question 20(a), we can proceed as follows
Uv/f = v+u
Where f=1
Then
uv/1= v+u
uv = v+u
uv-u=v
u(v-1) =v
u=v/v-1
therefore, the u that is associated with the minimum distance between
object and image is v/v-1

References
Chen, H. A. (2013). Coulomb drag between in-plane graphene double ribbons and the impact of the
dielectric constant. Nano research, 6, 56-71.
Cross, R. (2016). Coulomb's law for rolling friction. American Journal of Physics, 84, 376-389.
Schmidt, K. (2020). Exceptional coupling constants for the Coulomb–Dirac operator with anomalous
magnetic moment. Journal of Computational and Applied Mathematics, 363, 0377-0427.