Monte Carlo Integration and Variance Estimation
VerifiedAdded on 2019/09/30
|9
|2055
|438
Report
AI Summary
The provided code is a Python script that solves five questions related to Monte Carlo integration, estimation of pi, and variance calculations. The first question involves generating pairs of random numbers and plotting the function g(x) over the Omega region. The second question calculates the integral of g(x) over the region where h(x) >= 0 using the Monte Carlo method. The third question estimates the value of pi by integrating a specific function, which represents the area of a circle. The fourth question calculates the mean and standard deviation of the estimated integral values for different sample sizes. The fifth question plots the mean and standard deviation of the estimated integral values against the number of samples. Finally, the sixth question compares the true variance with the empirical variance calculated from the Monte Carlo estimates.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.
Last Name 1
Name:
Professor:
Course:
Date:
Project 1
Q1) Generation of N two-dimensional random co-ordinates in [0, 1]^2:
There is a direct instruction available in “numpy” for this task:
X = np.random.rand(N, 2)
To ensure reproducibility of the results, following command requires to be provided,
np.random.seed(1234) where 1234 is any arbitrary number.
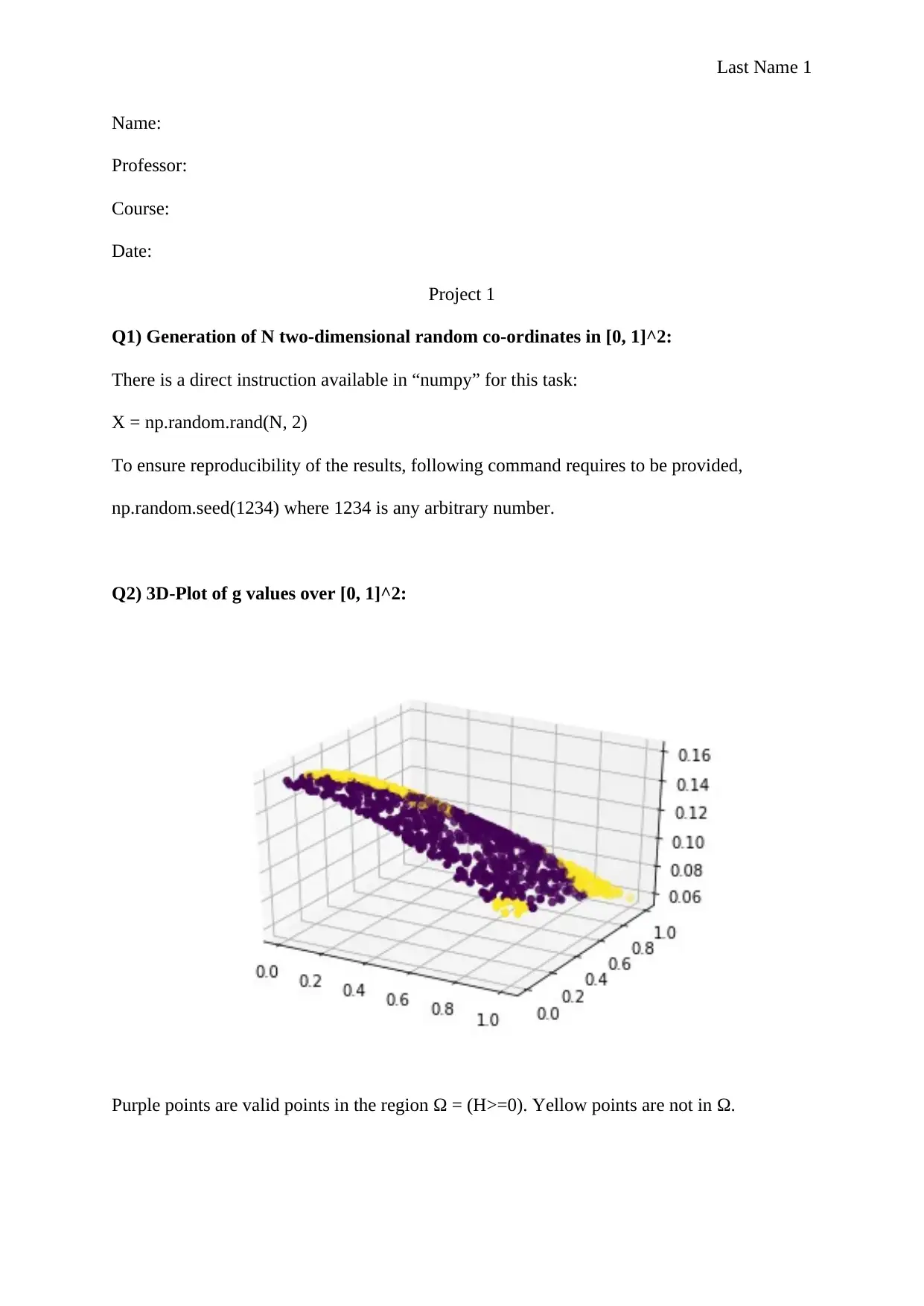
Q2) 3D-Plot of g values over [0, 1]^2:
Purple points are valid points in the region Ω = (H>=0). Yellow points are not in Ω.
Name:
Professor:
Course:
Date:
Project 1
Q1) Generation of N two-dimensional random co-ordinates in [0, 1]^2:
There is a direct instruction available in “numpy” for this task:
X = np.random.rand(N, 2)
To ensure reproducibility of the results, following command requires to be provided,
np.random.seed(1234) where 1234 is any arbitrary number.
Q2) 3D-Plot of g values over [0, 1]^2:
Purple points are valid points in the region Ω = (H>=0). Yellow points are not in Ω.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Last Name 2
Q3) Code for calculating integral of g over region Ω:
def my_Monte_Carlo():
X = np.random.rand(n, 2)
H = my_h_function(X)
G = my_g_function(X)
C = H >= 0
return sum(G*C)/n
The value of the integral is 0.03441.
Q4) Value of Pi by Monte Carlo Method:
def my_g_function(X):
m = len(X)
return np.array([1 for i1 in range(m)])
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(1 - x1**2 - x2**2)
return np.array(output)
n = 1000
np.random.seed(1234)
print("Estimate of Pi with 1000 pairs of random numbers", 4*my_Monte_Carlo())
Value of Pi is obtained as 3.128 (actual 3.142)
Q5) a) Mean and Standard Deviation for N=1000 and T=500
Mean = 0.03151
Standard Deviation = 0.001719
b) Plot of Mean and Standard Deviations for Nset Samples
# Q5(B) Mean and Standard deviation plots
Nset = np.round(np.logspace(1, 5, 100))
I, t0 = [], time.clock()
np.random.seed(1234)
for i in range(100):
Q3) Code for calculating integral of g over region Ω:
def my_Monte_Carlo():
X = np.random.rand(n, 2)
H = my_h_function(X)
G = my_g_function(X)
C = H >= 0
return sum(G*C)/n
The value of the integral is 0.03441.
Q4) Value of Pi by Monte Carlo Method:
def my_g_function(X):
m = len(X)
return np.array([1 for i1 in range(m)])
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(1 - x1**2 - x2**2)
return np.array(output)
n = 1000
np.random.seed(1234)
print("Estimate of Pi with 1000 pairs of random numbers", 4*my_Monte_Carlo())
Value of Pi is obtained as 3.128 (actual 3.142)
Q5) a) Mean and Standard Deviation for N=1000 and T=500
Mean = 0.03151
Standard Deviation = 0.001719
b) Plot of Mean and Standard Deviations for Nset Samples
# Q5(B) Mean and Standard deviation plots
Nset = np.round(np.logspace(1, 5, 100))
I, t0 = [], time.clock()
np.random.seed(1234)
for i in range(100):
Last Name 3
print(i, time.clock()-t0)
n = int(Nset[i])
J = []
for t in range(500):
J.append(my_Monte_Carlo())
I.append(np.array(J))
I = np.array(I)
plt.figure ()
plt.semilogx (Nset, I, 'kx')
plt.semilogx (Nset, np.mean(I, 1), 'b', label = 'mean')
plt.semilogx (Nset, np.mean(I, 1) + np.std(I, 1), 'r', label = 'mean +/- stdev')
plt.semilogx (Nset, np.mean(I, 1) - np.std (I, 1) , 'r')
plt.xlabel('number of samples')
plt.ylabel('estimated integral')
plt.legend()
plt.savefig("Q5.png")
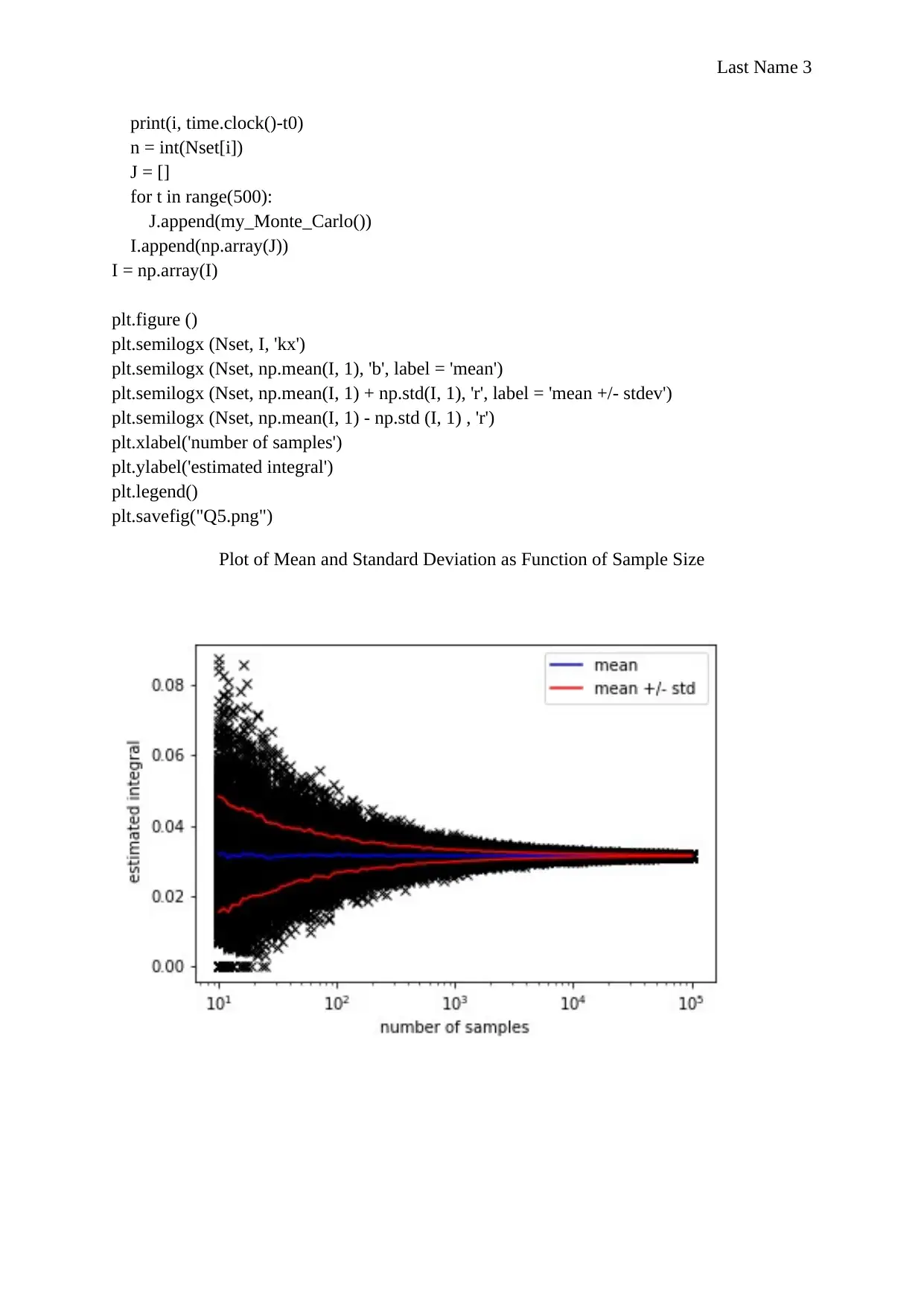
Plot of Mean and Standard Deviation as Function of Sample Size
print(i, time.clock()-t0)
n = int(Nset[i])
J = []
for t in range(500):
J.append(my_Monte_Carlo())
I.append(np.array(J))
I = np.array(I)
plt.figure ()
plt.semilogx (Nset, I, 'kx')
plt.semilogx (Nset, np.mean(I, 1), 'b', label = 'mean')
plt.semilogx (Nset, np.mean(I, 1) + np.std(I, 1), 'r', label = 'mean +/- stdev')
plt.semilogx (Nset, np.mean(I, 1) - np.std (I, 1) , 'r')
plt.xlabel('number of samples')
plt.ylabel('estimated integral')
plt.legend()
plt.savefig("Q5.png")
Plot of Mean and Standard Deviation as Function of Sample Size

Last Name 4
For number of samples >= 1150, the standard deviation is within 5% of mean value.
This value can be calculated using the following commands:
m = list(np.mean(I, 1)*0.05 >= np.std(I, 1)).index(True)
print(Nset[m])
Q6) Code and Plot
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
output = np.array(output)
output = output*output
return output
n = int(1e5)
np.random.seed(1234)
v2 = my_Monte_Carlo()
v = v2 - Intg*Intg
print("Variance for N = 100,000:", v)
V = np.array([v for i1 in range(len(Nset))])
plt.figure()
plt.semilogx(Nset, V ,label = 'true variance')
plt.semilogx (Nset, np.var(I, 1), 'r', label = 'empirical variance')
plt.xlabel('number of samples')
plt.ylabel('variance')
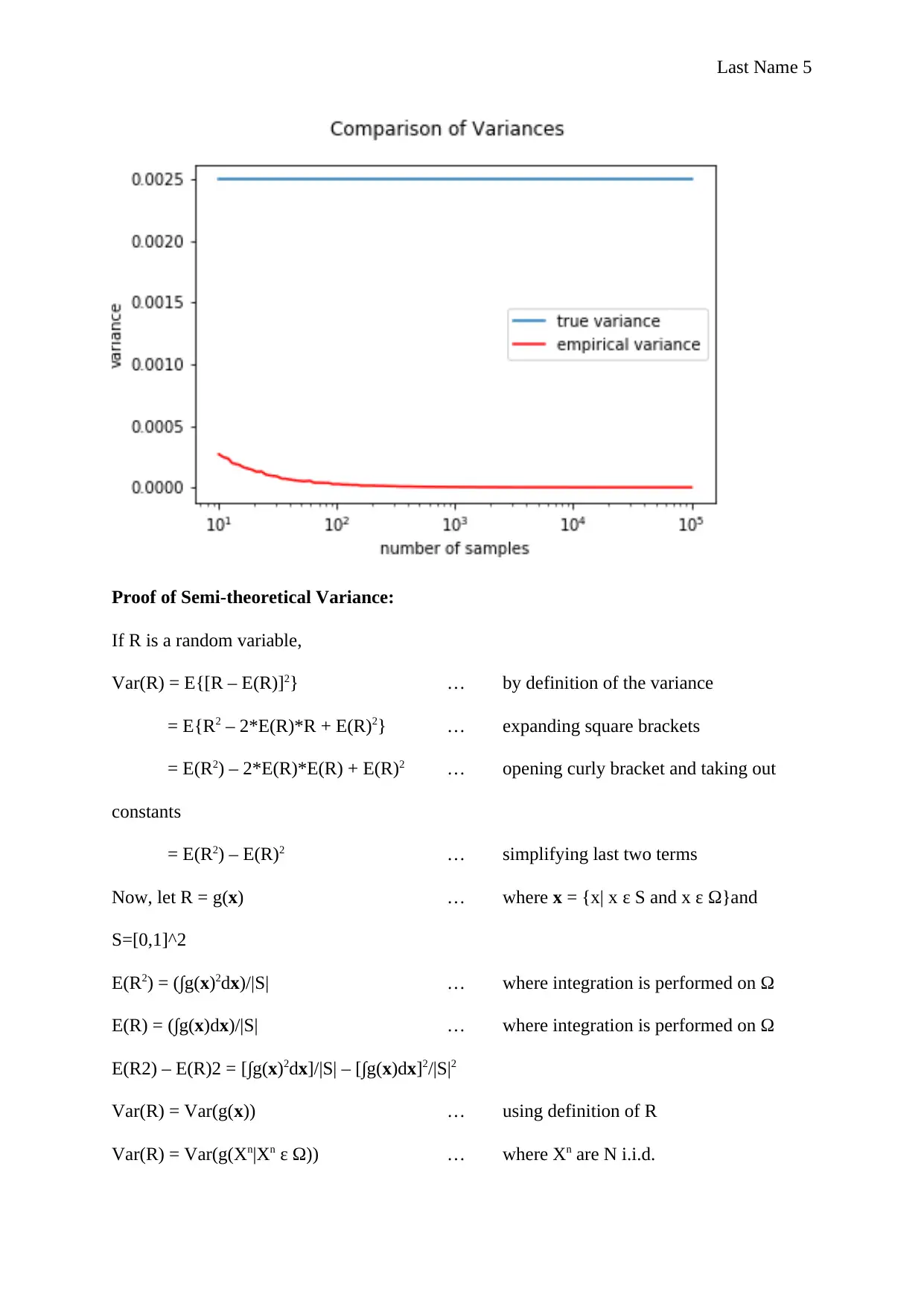
plt.suptitle("Comparison of Variances")
plt.legend()
plt.savefig("Q6.png")
For number of samples >= 1150, the standard deviation is within 5% of mean value.
This value can be calculated using the following commands:
m = list(np.mean(I, 1)*0.05 >= np.std(I, 1)).index(True)
print(Nset[m])
Q6) Code and Plot
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
output = np.array(output)
output = output*output
return output
n = int(1e5)
np.random.seed(1234)
v2 = my_Monte_Carlo()
v = v2 - Intg*Intg
print("Variance for N = 100,000:", v)
V = np.array([v for i1 in range(len(Nset))])
plt.figure()
plt.semilogx(Nset, V ,label = 'true variance')
plt.semilogx (Nset, np.var(I, 1), 'r', label = 'empirical variance')
plt.xlabel('number of samples')
plt.ylabel('variance')
plt.suptitle("Comparison of Variances")
plt.legend()
plt.savefig("Q6.png")
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Last Name 5
Proof of Semi-theoretical Variance:
If R is a random variable,
Var(R) = E{[R – E(R)]2} … by definition of the variance
= E{R2 – 2*E(R)*R + E(R)2} … expanding square brackets
= E(R2) – 2*E(R)*E(R) + E(R)2 … opening curly bracket and taking out
constants
= E(R2) – E(R)2 … simplifying last two terms
Now, let R = g(x) … where x = {x| x ε S and x ε Ω}and
S=[0,1]^2
E(R2) = (∫g(x)2dx)/|S| … where integration is performed on Ω
E(R) = (∫g(x)dx)/|S| … where integration is performed on Ω
E(R2) – E(R)2 = [∫g(x)2dx]/|S| – [∫g(x)dx]2/|S|2
Var(R) = Var(g(x)) … using definition of R
Var(R) = Var(g(Xn|Xn ε Ω)) … where Xn are N i.i.d.
Proof of Semi-theoretical Variance:
If R is a random variable,
Var(R) = E{[R – E(R)]2} … by definition of the variance
= E{R2 – 2*E(R)*R + E(R)2} … expanding square brackets
= E(R2) – 2*E(R)*E(R) + E(R)2 … opening curly bracket and taking out
constants
= E(R2) – E(R)2 … simplifying last two terms
Now, let R = g(x) … where x = {x| x ε S and x ε Ω}and
S=[0,1]^2
E(R2) = (∫g(x)2dx)/|S| … where integration is performed on Ω
E(R) = (∫g(x)dx)/|S| … where integration is performed on Ω
E(R2) – E(R)2 = [∫g(x)2dx]/|S| – [∫g(x)dx]2/|S|2
Var(R) = Var(g(x)) … using definition of R
Var(R) = Var(g(Xn|Xn ε Ω)) … where Xn are N i.i.d.

Last Name 6
Var(R) = Var(1/N/|S|*Σg(Xn|Xn ε Ω)) … using all N variables
= 1/N*{[∫g(x)2dx]/|S| – [∫g(x)dx]2/|S|2} … where x is vector of Xn
Simplifying,
Var(|S|/N*Σg(Xn|Xn ε Ω)) = |S|/N*[∫g(x)2dx] – 1/N*[∫g(x)dx]2
Thus, the required result is proven.
Annexure:
Full Code for the Six Problems:
# 2D Integration by Monte Carlo Method
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import time
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
return np.array(output)
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(x1**3 + x2**2 + 2*x1*x2 - math.sin(x1)
+ math.cos(2*math.pi*x1*x2) - 1)
return np.array(output)
# Q1 Generation of 1000 pairs of random numbers
n = 1000
np.random.seed(1234)
X = np.random.rand(n, 2)
# Q2 Plot of G over Omega region
# Evaluation of g and h at each pair
H = my_h_function(X)
Var(R) = Var(1/N/|S|*Σg(Xn|Xn ε Ω)) … using all N variables
= 1/N*{[∫g(x)2dx]/|S| – [∫g(x)dx]2/|S|2} … where x is vector of Xn
Simplifying,
Var(|S|/N*Σg(Xn|Xn ε Ω)) = |S|/N*[∫g(x)2dx] – 1/N*[∫g(x)dx]2
Thus, the required result is proven.
Annexure:
Full Code for the Six Problems:
# 2D Integration by Monte Carlo Method
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import time
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
return np.array(output)
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(x1**3 + x2**2 + 2*x1*x2 - math.sin(x1)
+ math.cos(2*math.pi*x1*x2) - 1)
return np.array(output)
# Q1 Generation of 1000 pairs of random numbers
n = 1000
np.random.seed(1234)
X = np.random.rand(n, 2)
# Q2 Plot of G over Omega region
# Evaluation of g and h at each pair
H = my_h_function(X)

Last Name 7
G = my_g_function(X)
C = H >= 0
# Plot Graph
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X[: ,0] , X[: ,1] , G, c=C)
plt.savefig("Q1.png")
# Q3 Function to find integral of g over omega
# Calculate integral of g over region for which h >= 0
def my_Monte_Carlo():
X = np.random.rand(n, 2)
H = my_h_function(X)
G = my_g_function(X)
C = H >= 0
return sum(G*C)/n
n = 1000
np.random.seed(1234)
Intg = my_Monte_Carlo()
print("Integral of g", Intg)
# Q4 Estimate of Pi
def my_g_function(X):
m = len(X)
return np.array([1 for i1 in range(m)])
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(1 - x1**2 - x2**2)
return np.array(output)
n = 1000
np.random.seed(1234)
print("Estimate of Pi with 1000 pairs of random numbers", 4*my_Monte_Carlo())
# Q5(A) Find mean and stdev of integral
# Mean and Standard deviation of integral
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
G = my_g_function(X)
C = H >= 0
# Plot Graph
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X[: ,0] , X[: ,1] , G, c=C)
plt.savefig("Q1.png")
# Q3 Function to find integral of g over omega
# Calculate integral of g over region for which h >= 0
def my_Monte_Carlo():
X = np.random.rand(n, 2)
H = my_h_function(X)
G = my_g_function(X)
C = H >= 0
return sum(G*C)/n
n = 1000
np.random.seed(1234)
Intg = my_Monte_Carlo()
print("Integral of g", Intg)
# Q4 Estimate of Pi
def my_g_function(X):
m = len(X)
return np.array([1 for i1 in range(m)])
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(1 - x1**2 - x2**2)
return np.array(output)
n = 1000
np.random.seed(1234)
print("Estimate of Pi with 1000 pairs of random numbers", 4*my_Monte_Carlo())
# Q5(A) Find mean and stdev of integral
# Mean and Standard deviation of integral
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Last Name 8
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
return np.array(output)
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(x1**3 + x2**2 + 2*x1*x2 - math.sin(x1)
+ math.cos(2*math.pi*x1*x2) - 1)
return np.array(output)
Ints, n = [], 1000
np.random.seed(1234)
for t in range(500):
Ints.append(my_Monte_Carlo())
Ints = np.array(Ints)
print("Mean =", Ints.mean())
print("Standard Deviation =", np.std(Ints))
# Q5(B) Mean and Standard deviation plots
Nset = np.round(np.logspace(1, 5, 100))
I, t0 = [], time.clock()
np.random.seed(1234)
for i in range(100):
print(i, time.clock()-t0)
n = int(Nset[i])
J = []
for t in range(500):
J.append(my_Monte_Carlo())
I.append(np.array(J))
I = np.array(I)
plt.figure ()
plt.semilogx (Nset, I, 'kx')
plt.semilogx (Nset, np.mean(I, 1), 'b', label = 'mean')
plt.semilogx (Nset, np.mean(I, 1) + np.std(I, 1), 'r', label = 'mean +/- stdev')
plt.semilogx (Nset, np.mean(I, 1) - np.std (I, 1) , 'r')
plt.semilogx (Nset, np.mean(I, 1)*1.05, 'g')
plt.xlabel('number of samples')
plt.ylabel('estimated integral')
plt.legend()
plt.savefig("Q5B2.png")
"""
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
return np.array(output)
def my_h_function(X):
output = []
for x in X:
x1, x2 = x
output.append(x1**3 + x2**2 + 2*x1*x2 - math.sin(x1)
+ math.cos(2*math.pi*x1*x2) - 1)
return np.array(output)
Ints, n = [], 1000
np.random.seed(1234)
for t in range(500):
Ints.append(my_Monte_Carlo())
Ints = np.array(Ints)
print("Mean =", Ints.mean())
print("Standard Deviation =", np.std(Ints))
# Q5(B) Mean and Standard deviation plots
Nset = np.round(np.logspace(1, 5, 100))
I, t0 = [], time.clock()
np.random.seed(1234)
for i in range(100):
print(i, time.clock()-t0)
n = int(Nset[i])
J = []
for t in range(500):
J.append(my_Monte_Carlo())
I.append(np.array(J))
I = np.array(I)
plt.figure ()
plt.semilogx (Nset, I, 'kx')
plt.semilogx (Nset, np.mean(I, 1), 'b', label = 'mean')
plt.semilogx (Nset, np.mean(I, 1) + np.std(I, 1), 'r', label = 'mean +/- stdev')
plt.semilogx (Nset, np.mean(I, 1) - np.std (I, 1) , 'r')
plt.semilogx (Nset, np.mean(I, 1)*1.05, 'g')
plt.xlabel('number of samples')
plt.ylabel('estimated integral')
plt.legend()
plt.savefig("Q5B2.png")
"""

Last Name 9
import shelve
#Save variable I
fname = "Shelf"
my_shelf = shelve.open(fname, 'n')
my_shelf["I"]=globals()["I"]
my_shelf.close()
#Load variable I
my_shelf = shelve.open("Shelf")
globals()["I"] = my_shelf["I"]
my_shelf.close()
"""
# Q6 Semitheoretical versus Empirical Variances
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
output = np.array(output)
output = output*output
return output
n = int(1e5)
np.random.seed(1234)
v2 = my_Monte_Carlo()
v = v2 - Intg*Intg
print("Variance for N = 100,000:", v)
V = np.array([v for i1 in range(len(Nset))])
plt.figure()
plt.semilogx(Nset, V ,label = 'true variance')
plt.semilogx (Nset, np.var(I, 1), 'r', label = 'empirical variance')
plt.xlabel('number of samples')
plt.ylabel('variance')
plt.suptitle("Comparison of Variances")
plt.legend()
plt.savefig("Q6.png")
import shelve
#Save variable I
fname = "Shelf"
my_shelf = shelve.open(fname, 'n')
my_shelf["I"]=globals()["I"]
my_shelf.close()
#Load variable I
my_shelf = shelve.open("Shelf")
globals()["I"] = my_shelf["I"]
my_shelf.close()
"""
# Q6 Semitheoretical versus Empirical Variances
def my_g_function(X):
output = []
for x in X:
x1, x2 = x
output.append(0.5/math.pi*math.exp(-0.5*(x1**2 + x2**2)))
output = np.array(output)
output = output*output
return output
n = int(1e5)
np.random.seed(1234)
v2 = my_Monte_Carlo()
v = v2 - Intg*Intg
print("Variance for N = 100,000:", v)
V = np.array([v for i1 in range(len(Nset))])
plt.figure()
plt.semilogx(Nset, V ,label = 'true variance')
plt.semilogx (Nset, np.var(I, 1), 'r', label = 'empirical variance')
plt.xlabel('number of samples')
plt.ylabel('variance')
plt.suptitle("Comparison of Variances")
plt.legend()
plt.savefig("Q6.png")
1 out of 9
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.

