Coefficient of Portfolio Management Correlation and Diversification

Expected return of discrete distribution How to calculate return and risk of continous distribution What is coeffiecient of varaince Covariance Portfolio management Correlation and diversification What are the type sof risks Risk market line Abstract In investment, especially in the portfolio management, the risk and returns are two significant measures in making investment decisions.This paper endeavors to furnish a concise theoretical explanation with examples on identifying the return and related risk.The delineations of tables can essentially contribute to the comprehension of a

Learning outcomes
 How to calculate return and risk of discrete distribution
 How to calculate return and risk of continous distribution
 What is coeffiecient of varaince
 Covariance
 Portfolio management
 Correlation and diversification
 What are the type sof risks
 Security market line
Abstract
In investment, especially in the portfolio management, the risk and returns are two significant
measures in making investment decisions.This paper endeavors to furnish a concise
theoretical explanation with examples on identifying the return and related risk.The
delineations of tables can essentially contribute to the comprehension of a reader about to risk
and return.Basically in this chapter discuss about risk and return of discrete and continuous
distribution,portfolio management,systematic risk and security market line

01.Risk and return in discrete distribution
01.01.Return
 Income received on a investment plus any changes in market price
 Usually expressed as a percentage of the beginning market price of the investment.
01.01.01.Probability distribution
Illustration 01.
Find the estimated rate of return of A & B
Table 01.
Economin
condition
Probabi.of
occurrence
Return A % Return B % Estimated
return A %
Estimated
return B %
Boom 0.5 19 30 9.5 15
Bust 0.5 13 -5 6.5 -2.5
Estimated return 16 12.5
01.02.Risk
 The variability of returns from those are expected
 Two methods are available for the calculation of risk
 Using range
 Using standard deviation
01.02.01..Using standard deviation method
Illustration 02.
Find the standard deviation of company A using above illustration 01.
Table 02.
Economin
condition
Probabi.of
occurrence(P
Return(R) Estimated
return(ER)
(R-ER)2 (R-ER)2*P
R=[D+(Pt-Pt-1)]/Pt-1
 R=Return
 D=Divident
 Pt=price at the end of year
 Pt-1=Price at the end of
previous year

)
Boom 0.5 0.19 0.16 0.0009 0.00045
Bust 0.5 0.12 0.16 0.0016 0.00080
Variance 0.00125
 Standard deviation=√0.00125=0.03535=3.535%
 Using the above method we can calculate the standard deviation of company B also
02.Coefficient of variance
 Statistical measure of the relative scattering of data points in an data arrangement
around the mean
 In finance, the coefficient of variance permits investors to decide how much
unpredictability,or risk, is accepted in contrast with the amount of return anticipated
from investment (HAYERS, n.d.)
03.Expected return and risk in continuous distribution
03.01.Expected return 03.02.Risk
04.Covariance
 Statistical term used in security and portfolio evaluation.It measures the amount
which two assets move in relation to each other
 Positive covariance = assets move in same direction
05.Portfolio management
05.01.Expected return
σ=√[ Σ(Ri-R)2 ]/n
CV = σ σ=standard deviation
μ μ=Mean
R= Σ (Ri)/(n)
n
I=1
n
I=1
R=expected rate for asset
Ri=return for the ith observation
n= Total No. of observations
COV(X,Y)= [Σ(Xi-X)(Yi-Y)]/(n-1)
RP= Σ (Wi)(Ri)
n
I=1
Rp=expected rate for portfolio
Wi=weight for ith asset
Ri=expected rate of i asset

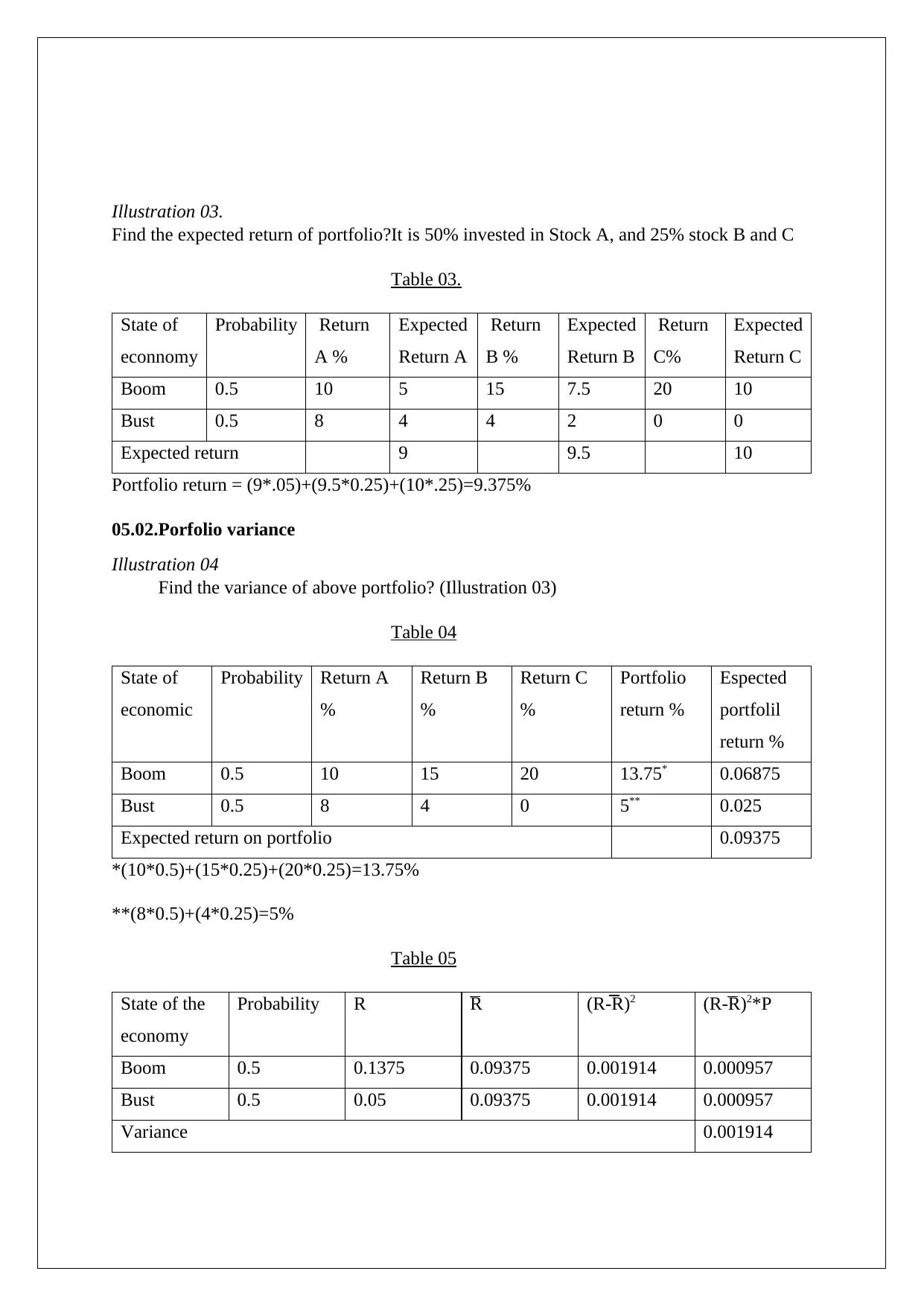
Illustration 03.
Find the expected return of portfolio?It is 50% invested in Stock A, and 25% stock B and C
Table 03.
State of
econnomy
Probability Return
A %
Expected
Return A
Return
B %
Expected
Return B
Return
C%
Expected
Return C
Boom 0.5 10 5 15 7.5 20 10
Bust 0.5 8 4 4 2 0 0
Expected return 9 9.5 10
Portfolio return = (9*.05)+(9.5*0.25)+(10*.25)=9.375%
05.02.Porfolio variance
Illustration 04
Find the variance of above portfolio? (Illustration 03)
Table 04
State of
economic
Probability Return A
%
Return B
%
Return C
%
Portfolio
return %
Espected
portfolil
return %
Boom 0.5 10 15 20 13.75* 0.06875
Bust 0.5 8 4 0 5** 0.025
Expected return on portfolio 0.09375
*(10*0.5)+(15*0.25)+(20*0.25)=13.75%
**(8*0.5)+(4*0.25)=5%
Table 05
State of the
economy
Probability R R (R-R)2 (R-R)2*P
Boom 0.5 0.1375 0.09375 0.001914 0.000957
Bust 0.5 0.05 0.09375 0.001914 0.000957
Variance 0.001914

Variance = 0.001914
06.Correlation and diversification
07.Total risk
Total Risk = systematic risk + unsystematic risk
07.01.systematic risk
 influence a larger number of assets,each to a greater or lesser extend
 influence from certain economic wide factors
 Examples (Ross, Westerfield, & Jordan)
 Money supply, inflation , level of government expending
07.02.unsystematic risk
 Affect a single asset or small number of assets
 These risk are unique to individual companies or assets
 Examples (Ross, Westerfield, & Jordan)
 Emergence of new competitors , plant breakdown , law suit
07.03.Systematic risk principle
 Systematic risk principle state that the reward for bearing risk depends only on the
systematic risk of an investment.
07.04.Measuring the systematic risk
 To measure systematic risk we use Beta (β) coeffitient
 A beta tells us how much systematic risk a particular asset has relative to an average
asset
 What is beta?
-1 0 +1
Perfectly
negative
Perfectly
positive
 More negative correlation
 More diversified
 Lower the risk
 More positive correlation
 less diversified
 higher the risk

Rj = required rate of return for stock j
Rf = risk free rate of return
βj = beta of stock j
Rm= expected rate of return for market
portfolio
It measure the sensitivity of a stock’s returns to changes in returns on the market
portfolio
07.05.Calculation of Beta
 Rjt = α + βRmt + Ɛj
Beta represent the slope of the above function
 βj = [cov((Rj , Rm)]/ σm2
Illustration 05
Find the beta ?
Table 06
Year Rj Rm Rj-Rj (1) Rmt-Rm(2) 1*2 σm2
1 11 13 3 3 9 9
2 7 9 -1 -1 1 1
3 6 8 -2 -2 4 4
Rj = 8 Rm = 10 14 14/2
Cov = 14/2 = 7 σm2 = 14/2 = 7 β = 7/7 = 1
08.Security market line
Risk premium-earn of excess return because it is the adiitional return we earn by moving
from a relatively risk free investment to a risky one.It can be interpret as reward for bearing.
(Hayes, n.d.)
08.01..Capital asset pricing model
 The equation of the SML showing the relationship between expected return & beta
 Assumptions
 Capital market are efficient
 Homogeneous investor expectation over a given period
 Risk free return is certain
cov(Rj , Rm) = Σ [(Rj-Rj)(Rmt-Rm)]/(n-1)
n
I=0
Rj = Rf + βj (Rm - Rf)
Market risk premium
risk premium

 Market portfolio contains only systematic risk
Summary
1. Return(discrete distribution) of an investment can be expressed as
R=[D+(Pt-Pt-1)]/Pt-1
2. Coefficient of variance is used to find the risk per return
3. Risk can reduce using portfolio investment
4. Covariance measures the amount which two assets move in relation to each
other
5. There is a reward for bearing the risk. This reward is the “risk premium”
6. Total risk can divided into two parts. They are systematic and unsystematic
risk
7. Unsystematic risk can eliminated through diversification. Therefore Risk
Premium is only for the systematic risk.
8. Systematic risk can measure using Beta Coefficient
9. Expected return of an asset is equal to the risk free rate plus risk premium
(E)Rj = Rf + βj ((E)Rm - Rf)
This is the equation of security market line and this is called Capital Asset
Pricing Model as well.