Lecture Notes: Recurrence Relations and Algorithms

This lecture notes covers topics such as recursive algorithms, Towers of Hanoi, and recurrence relations. It explains the concept of solving problems using recursion and provides an example of Towers of Hanoi problem. It also discusses the use of recurrence relations in generating sequences.

Lecture Notes
Computational Problem Solving
Week 7:
Recurrence Relations and Algorithms
Contents
Recursive Algorithms ............................................................................................................................................. 1
Towers of Hanoi .................................................................................................................................................... 1
Recurrence Relations ............................................................................................................................................ 5
Second Order Linear Homogeneous Recurrence Relations .................................................................................. 8
Application: Fibonacci and Lucas Recurrence Relations ....................................................................................... 9
Extension Topic: General Homogeneous Recurrence Relations ......................................................................... 11
Extension Topic: Non-homogeneous Recurrence Relations ........................................................................... 12
Recursion in Python ............................................................................................................................................ 13
Recursive Algorithms
Recursive algorithms are those that call themselves. For example, to find the factorial of an integer is:
5! = 5 × 4 × 3 × 2 × 1
And more generally as:
𝑛! = 𝑛 ×(𝑛 − 1) × (𝑛 − 2) × … × 3 × 2 × 1
As (𝑛 − 1)! =(𝑛 − 1) × (𝑛 − 2) × … × 3 × 2 × 1we can rewrite the above as:
𝑛! = 𝑛 ×(𝑛 − 1)!
Where 1! = 1as a base condition. As we can see recursive algorithms have similar ideas to what we used to
prove statements by mathematical induction.
Towers of Hanoi
This involves n discs of various sizes on three posts

The disc starts on one of the posts with the largest disc on the bottom of the stack, with the smaller discs
resting on top of a larger disc, so ordered with respect to size.
The exercise is to move all the discs to another post, with the largest on the bottom and the smallest on top
without a larger disc resting on a small disc.
The question is: what is the minimum number of moves needed?
Understanding the Problem:
Objective:
Place the pile of discs on a different peg
Constraints:
- no disc can sit on a smaller disc
- only top disc may be moved
- you can only move one disc at a time
We are being asked to work out the minimum number of moves to move the discs from one peg to another.
We could build a model of the problem (as it was originally in Vietnam). Or we can use diagrams to help us
model the moves. We cannot really restate the problem.
The unknown is the minimum number of moves as well as the number of discs. Also, we are not sure how we
can make those moves to obtain the minimal number of moves. We have not made any assumptions apart
from the constraints of the problem and that there are a fixed number of pegs which is 3 (i.e. we are not
generalising the number of pegs).
Devising a Plan
We haven’t solved this problem before. However, we have looked at noughts and crosses. In that problem we
broke it down by seeing what happens if we add an extra column or row.
We can do a similar approach here too. We can look at the number of moves for 1 disc, 2 discs, etc to see if
we can build up a pattern.
We can then look to see how we make those moves for 2 discs, 3 discs to see what happens if we add a disc
to the source peg. We already said in part (1) that we can use diagrams to help us.
We haven’t left anything out from the problem statement. To move three discs, we may find via trial and
error:

Following a similar strategy, we may find the number of ways to move the discs when we have 2, 3, 4, etc
discs.
Number of discs Number of moves breakdown
1 1 1
2 3 1 + 1 + 1
3 7 3 + 1 + 3
4 15 7 + 1 + 7
5 31 15 + 1 + 15
Generalising this, we may find the number of moves is:
(number of moves for 𝑛 − 1discs) + 1 + (number of moves for 𝑛 − 1discs)
Alternatively, we may note that the number of moves is one less than a power of 2. Therefore, the number of
moves is 2𝑛 − 1. Hence given 𝑛 discs on a peg it will take 2𝑛 − 1moves (minimum) to move the discs from
one peg to another peg given the constraints. But, how do we make those moves? This is where the first
strategy proves helpful. To write an algorithm for Tower of Hanoi, first we need to learn how to solve this
problem with lesser amount of discs, say → 1 or 2. We mark three towers with
name, source, destination and aux (only to help moving the discs). If we have only one disc, then it can easily
be moved from source to destination peg.
If we have 2 discs −
• First, we move the smaller (top) disc to aux peg.
• Then, we move the larger (bottom) disc to destination peg.
• And finally, we move the smaller disc from aux to destination peg.
If we then say that the larger (bottom) disc is the rest of the discs and using the relationship between the
number of moves: number of moves for 𝑛 − 1discs) + 1 + (number of moves for 𝑛 − 1discs), we can form a
generalised strategy.

Approach:
• Recursively Move N-1 disc from source to Auxiliary peg.
• Move the last disc from source to destination.
• Recursively Move N-1 disc from Auxiliary to destination peg
The steps to follow are:
Step 1 − Move n-1 discs from source to aux
Step 2 − Move nth disc from source to dest
Step 3 − Move n-1 discs from aux to dest
From which we can produce pseudo-code to solve the Towers of Hanoi
problem.
START Procedure Hanoi(disc, source, dest, aux)
IF disc == 1, THEN
move disc from source to dest
ELSE
Hanoi(disc - 1, source, aux, dest) // Step 1
move disc from source to dest // Step 2
Hanoi(disc - 1, aux, dest, source) // Step 3
END IF
END Procedure STOP
Which, in Python, is:
def TowerOfHanoi(n , source, destination, auxiliary):
if n==1:
print ("Move disc 1 from source",source,"to destination",destination)
return
TowerOfHanoi(n-1, source, auxiliary, destination)
print ("Move disc",n,"from source",source,"to destination",destination)
TowerOfHanoi(n-1, auxiliary, destination, source)
# test code
n = 4
TowerOfHanoi(n,'A','B','C')
# A, C, B are the name of rods
To test this, we may look at the solutions or prove it via induction.
For the Tower of Hanoi, we have the number of moves, 𝑆𝑛 is 𝑆𝑛 = 2𝑛 − 1for 𝑛 discs, this is our 𝑃(𝑛).

Base case, 𝑃(1): 𝑆1 = 21 − 1 = 2 − 1 = 1. We know it takes one move to move one disc, so 𝑃(1)is true.
We assume that 𝑃(𝑘): 𝑆𝑘 = 2𝑘 − 1is true.
Now, for 𝑃(𝑘 + 1): 𝑆𝑘+1 = 2𝑘+1 − 1
𝑆𝑘+1 = (𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑚𝑜𝑣𝑒𝑠 𝑟𝑒𝑞𝑢𝑖𝑟𝑒𝑑 𝑡𝑜 𝑚𝑜𝑣𝑒 𝑘 𝑑𝑖𝑠𝑐𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑏𝑜𝑡𝑡𝑜𝑚 𝑑𝑖𝑠𝑘)
+ (1 𝑚𝑜𝑣𝑒 𝑡𝑜 𝑚𝑜𝑣𝑒 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑑𝑖𝑠𝑐)
+ (𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑚𝑜𝑣𝑒𝑠 𝑟𝑒𝑞𝑢𝑖𝑟𝑒𝑑 𝑡𝑜 𝑚𝑜𝑣𝑒 𝑡ℎ𝑒 𝑘 𝑑𝑖𝑠𝑐𝑠 𝑏𝑎𝑐𝑘 𝑜𝑛𝑡𝑜 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑑𝑖
= 𝑆𝑘 + 1 + 𝑆𝑘 = 2𝑆𝑘 + 1 = 2(2𝑘 − 1) + 1
= 2 × 2𝑘 − 2 + 1 = 21 × 2𝑘 − 1 = 2𝑘+1 − 1
Hence 𝑃(𝑘 + 1) is true provided that 𝑃(𝑘)is true.
Therefore, by mathematical induction, the number of moves for the Tower of Hanoi is 𝑆𝑛 = 2𝑛 − 1
We therefore have the number of moves is 2𝑛 − 1. We note that:
𝑆1 = 1
𝑆2 = 3 = 2 × 1 + 1 = 2𝑆1 + 1
𝑆3 = 7 = 2 × 3 + 1 = 2𝑆2 + 1
𝑆4 = 15 = 2 × 7 + 1 = 2𝑆3 + 1
By looking at the pattern, we have
𝑆𝑛 = 2𝑆𝑛−1 + 1, 𝑆1 = 1
As our recursive formula.
Assessing the result:
Our solutions meets the requirements, we have found the minimal number of moves and how to make those
moves using recursion. We can then test the algorithm on 2 discs and 3 discs, etc and we get the correct
number of moves as well as the method to achieve those moves.
We could possibly make some aspects easier; however, the most simple solution in this case is the recursive
approach
Describing what we have learnt:
We learnt that we can use recursion to help solve problems and strengthen the idea of breaking a problem up
to look at simpler cases before generalising.
This problem was difficult in that the approach used is different to the noughts and crosses problem due to
the increased complexity of the solution and the exponential nature of number of moves rather than the
quadratic nature.
Documenting the solution:
Reread our solution, is there anything that should be rewritten?
Not in this case, we cannot see anything that is difficult to understand
Recurrence Relations
We have already met recurrence relations, although not formally defined what they are. Consider the
following instructions for generating a sequence:
1. Start with 5

2. Given any term, add 3 to get the next term
If we list the terms of this sequence, we obtain
5, 8, 11, 14, 17, …
The first term is 5 because of instruction 1.
The second term is 8 because instruction 2 says to add 3 to 5 to get the next term, 8
The third term is 11 because instruction 2 says to add 3 to 8 to get the next term, 11, etc
Instructions 1 and 2 do not give an explicit formula for the nth term of the sequence in the sense of providing
a formula that we can plug n into to obtain the value of the nth term, but by computing term by term we can
eventually compute any term of the sequence.
If we denote the sequence as 𝑎1, 𝑎2, …, we may rephrase instruction 1 as
𝑎1 = 5
And instruction 2 as:
𝑎𝑛 = 𝑎𝑛−1 + 3, 𝑛 ≥ 2
𝑎1 = 5
𝑎𝑛 = 𝑎𝑛−1 + 3, 𝑛 ≥ 2
If we take 𝑛 = 2, we obtain 𝑎2 = 𝑎1 + 3 = 5 + 3 = 8
If we take 𝑛 = 3, we obtain 𝑎3 = 𝑎2 + 3 = 8 + 3 = 11
We can then compute any term in the sequence just as we did with instructions 1 and 2. The instructions
above are equivalent to this.
This equation is an example of a recurrence relation. A recurrence relation defines a sequence by giving the
nth value in terms of its previous values. In order for a recurrence relation to define a sequence, a start up
value (or initial conditions) must be given.
Consider the following instructions for generating a sequence:
1. Start with 5
2. Given any term, add 3 to get the next term
The following forms the function recursively (on the left) and iteratively (on the right).
Now, we will write the formal definition of a recurrence relation.
Definition 7.1
A recurrence relation for the sequence
𝑎0, 𝑎1, 𝑎2, …
Is an equation that relates 𝑎𝑛 to its predecessors 𝑎0, 𝑎1, … 𝑎𝑛−1
Initial conditions for the sequence 𝑎0, 𝑎1, …are explicitly given values for a finite number of the terms of
the sequence

For example, the Fibonacci sequence is defined by the recurrence relation
𝑓𝑛 = 𝑓𝑛−1 + 𝑓𝑛−2 𝑛 ≥ 3
With initial conditions 𝑓1 = 1, 𝑓2 = 1
We can form this sequence both recursively (on the left) and iteratively (on the right).
We can now have some definition. The first is a linear homogeneous recurrence relation and the second is for
the non-homogeneous case.
Definition 7.2
A linear homogeneous recurrence relation of order 𝑘 with constant coefficients is a recurrence relation of
the form
𝑎𝑛 = 𝑐1𝑎𝑛−1 + 𝑐2𝑎𝑛−2 + ⋯ + 𝑐𝑘𝑎𝑛−𝑘 , 𝑐𝑘 ≠ 0
Notice that a linear homogeneous recurrence relation of order 𝑘 with constant coefficients, together with
the 𝑘 initial conditions
𝑎0 = 𝐶0, 𝑎1 = 𝐶1, … , 𝑎𝑘−1 = 𝐶𝑘−1
Uniquely defines a sequence 𝑎0, 𝑎1, ….
Similarly, we have non-homogeneous relations:
Definition 7.3
A linear non-homogeneous recurrence relation of order 𝑘 with constant coefficients is a recurrence
relation of the form
𝑎𝑛 = 𝑐1𝑎𝑛−1 + 𝑐2𝑎𝑛−2 + ⋯ + 𝑐𝑘𝑎𝑛−𝑘 + 𝑓(𝑎), 𝑐𝑘 ≠ 0
In other words, a non-homogenous recurrence has extra terms which are not related to previous terms.
If 𝑓(𝑎) = 0 then it is homogeneous.
In this module, we only look at the homogeneous cases and mostly the second order cases. This is because
this is a computer science course and to solve generalised cases involve more maths. The most important
takeaway is to understand what a recurrence relation is and how we can produce the sequence using
recursion.
Going back to the (infamous) Fibonacci sequence, the relation
𝑓𝑛 = 𝑓𝑛−1 + 𝑓𝑛−2
is an example of a linear homogeneous recurrence relation of order 2.
Worked Example:
What is the order of the following recurrence relations? Are they homogeneous or non-
homogeneous?
a) 𝑎𝑛 = 11𝑎𝑛−1 − 39𝑎𝑛−2 + 45𝑎𝑛−3 Third order, homogeneous.
b) 𝑎𝑛 = 𝑎𝑛−1 + 2𝑎𝑛−2 Second order, homogeneous
c) 𝑥𝑛 = 𝑥𝑛−2 Second order, homogeneous

d) 𝑎𝑛 = 𝑎𝑛−1 + 4 First order, non-homogeneous
e) 𝑎𝑛 = 5𝑎𝑛−1 − 4𝑎𝑛−2 + 𝑛2 Second order, non-homogeneous.
Your turn:
What is the order of the following recurrence relations? Are they homogeneous or non-
homogeneous?
a) 𝑎𝑛 = 3𝑎𝑛−1 + 𝑎𝑛−2 + 𝑎𝑛−4
b) 𝑎𝑛 = 5𝑎𝑛−1 − 3𝑎𝑛−2 − 1
Second Order Linear Homogeneous Recurrence Relations
Let
𝑎𝑛 = 𝑐1𝑎𝑛−1 + 𝑐2𝑎𝑛−2
Be a second order, linear homogeneous recurrence relation with constant coefficients.
If 𝑆and 𝑇are solutions, then 𝑈 = 𝑏𝑆 + 𝑑𝑇is also a solution of *.
If 𝑟 is a root of the characteristic (or auxiliary) equation defined as:
𝑡2 − 𝑐1𝑡 − 𝑐2 = 0
Then the sequence 𝑟𝑛, 𝑛 = 0,1, …is a solution. If 𝑎 is the sequence defined by *,
𝑎0 = 𝐶0, 𝑎1 = 𝐶1
And 𝑟1 and 𝑟2 are roots of * with 𝑟1 ≠ 𝑟2, then there exist constants 𝑏 and 𝑑 such that
𝑎𝑛 = 𝑏𝑟1
𝑛 + 𝑑𝑟2
𝑛
This is called the general solution.
Given a set of initial conditions, finding the values of 𝑏 and 𝑑 result in the particular solution.
Worked Example:
What is the general and particular solutions to the recurrence relation 𝑎𝑛 = 7𝑎𝑛−1 − 12𝑎𝑛−2 with
initial conditions 𝑎1 = 1 and 𝑎2 = 4?
Rearranging gives:
Therefore, the characteristic solution is:
𝑡2 − 7𝑡 + 12 = 0
This can be factorised as
(𝑡 − 4)(𝑡 − 3) = 0
And has solutions 𝑡 = 4and 𝑡 = 3. Therefore, the general solution is
𝑎𝑛 = 𝑏 × 4𝑛 + 𝑑 × 3𝑛
Substituting the first two values in 𝑎1 = 1 and 𝑎2 = 4 gives
𝑎1: 1 = 4𝑏 + 3𝑑

𝑎2: 4 = 16𝑏 + 9𝑑
Solving these simultaneous equations gives the solution 𝑏 =1
4 and 𝑑 = 0.
Therefore, the particular solution is 𝑎𝑛 = 1
4 × 4𝑛 + 0 × 3𝑛 = 1
4 × 4𝑛 or 𝑎𝑛 = 4𝑛−1
Your turn:
What is the general and particular solutions to the recurrence relation 𝑎𝑛 = 7𝑎𝑛−1 − 12𝑎𝑛−2 with
initial conditions 𝑎1 = 1 and 𝑎2 = 3
Application: Fibonacci and Lucas Recurrence Relations
The relation
𝑓𝑛 = 𝑓𝑛−1 + 𝑓𝑛−2
Can be rewritten as 𝑓𝑛 − 𝑓𝑛−1 − 𝑓𝑛−2, 𝑛 ≥ 3and initial conditions 𝑓1 = 1, 𝑓2 = 1.
We begin by using the quadratic formula to solve
𝑡2 − 𝑡 − 1 = 0
The solution of this quadratic is 𝑡 =1±√5
2
𝑡 =1 ±√5
2
Thus, the general solution is:
𝑓𝑛 = 𝑏( 1 +√5
2 )
𝑛
+ 𝑑( 1 −√5
2 )
𝑛
To find the particular solution:
𝑓𝑛 = 𝑏( 1 +√5
2 )
𝑛
+ 𝑑( 1 −√5
2 )
𝑛
To satisfy the initial conditions, we must have
𝑏( 1 +√5
2 ) + 𝑑( 1 −√5
2 ) = 1
And
𝑏( 1 +√5
2 )
2
+ 𝑑( 1 −√5
2 )
2
= 1
𝑓𝑛 = 𝑏( 1 +√5
2 )
𝑛
+ 𝑑( 1 −√5
2 )
𝑛
Using the initial conditions and the first term of the sequence, we have:

𝑓1 = 1 ⇒ 𝑏( 1 +√5
2 ) + 𝑑( 1 −√5
2 ) = 1
Which results in:
𝑏(1 + √5) + 𝑑(1 − √5) = 2
Taking the second term in the sequence.
𝑓2 = 1 ⇒ 𝑏( 1 +√5
2 )
2
+ 𝑑( 1 −√5
2 )
2
= 1
Which results in:
𝑏(3 + √5) + 𝑑(3 − √5) = 2
We then have the system of equations:
𝑏(1 + √5) + 𝑑(1 − √5) = 2
𝑏(3 + √5) + 𝑑(3 − √5) = 2
Which can be solved simultaneously for 𝑏 and 𝑑, to obtain
𝑏 = 1
√5, 𝑑 = −
1
√5
Therefore, the particular solution is:
𝑓𝑛 = 1
√5( 1 +√5
2 )
𝑛
− 1
√5( 1 −√5
2 )
𝑛
Surprisingly, even though 𝑓𝑛 is an integer, the formula involves the irrational number √5.
The number 1+√5
2 which is called the golden ratio, 𝜙 = 1+√5
2 and has the property 1
𝜙 = 𝜙 − 1.
The Fibonacci sequence is fascinating and has many interesting properties.
The first eight Fibonacci numbers is then
1, 1, 2, 3, 5, 8, 13, 21, …
If we sum these, we get
1, 2, 4, 7, 12, 20, 𝑒𝑡𝑐
These look like they are one less than term two ahead, I,e,
𝑓1 + 𝑓2 + ⋯ + 𝑓𝑛 = 𝑓𝑛+2 − 1
We can prove this by mathematical induction:
Let 𝑃(𝑛): 𝑓1 + 𝑓2 + ⋯ + 𝑓𝑛 = 𝑓𝑛+2 − 1
Then,
𝑓1 = 1, 𝑓3 − 1 = 2 − 1 = 1
So, 𝑃(1)is true.
Assuming 𝑃(𝑘): 𝑓1 + 𝑓2 + ⋯ + 𝑓𝑘 = 𝑓𝑘+2 − 1is true, then
𝑃(𝑘 + 1): 𝑓1 + 𝑓2 + ⋯ + 𝑓𝑘 + 𝑓𝑘+1 = 𝑓𝑘+3 − 1

Now, as 𝑃(𝑘)is true
𝑓𝑘+2 − 1 + 𝑓𝑘+1 = 𝑓𝑘+3 − 1
As 𝑓𝑘+1 + 𝑓𝑘+2 = 𝑓𝑘+3 by definition. Therefore 𝑃(𝑘 + 1)is true. Therefore, by mathematical induction, as
𝑃(𝑘) → 𝑃(𝑘 + 1)is true and 𝑃(1)is true, then
𝑓1 + 𝑓2 + ⋯ + 𝑓𝑛 = 𝑓𝑛+2 − 1
Extension Topic: General Homogeneous Recurrence Relations
This section is not examinable.
So far, we have only considered recurrence relations whose characteristic equation results in two distinct
solutions. Sometimes when solving a quadratic equation, you might get a repeated solution or no real
solution. We will consider here those types of recurrence relations.
If we have repeated (equal) roots of the characteristic equation, we have to make a slight modification as can
be seen in the following example.
To solve the recurrence relation 𝑎𝑛 = 6𝑎𝑛−1 − 9𝑥𝑛−2, we first look at the characteristic equation 𝑚2 −
6𝑚 + 9 = 0which factorises to (𝑚 − 3)(𝑚 − 3) = 0 with the solution 𝑚 = 3. Therefore, the general
solution would look like 𝑎𝑛 = 𝐴 × 3𝑛 where normally we would expect two solutions for a second order
recurrence relation. If we consider the expression 𝑎𝑛 = 𝑛 × 3𝑛, then 𝑎𝑛−1 = (𝑛 − 1) × 3𝑛−1 and 𝑎𝑛−2 =
(𝑛 − 2) × 3𝑛−2. Substituting these into the recurrence relation, we have:
𝐿𝐻𝑆 = 𝑛 × 3𝑛
𝑅𝐻𝑆 = 6(𝑛 − 1) × 3𝑛−1 + 18 × 3𝑛−2
= 6𝑛 × 3𝑛−1 − 9𝑛 × 3𝑛−2 − 6 × 3𝑛−1 + 18 × 3𝑛−2
= 2𝑛 × 3𝑛 − 𝑛 × 3𝑛 = 𝑛 × 3𝑛 = 𝐿𝐻𝑆
Therefore, the left- and right-hand sides are equal and 𝑛 × 3𝑛 is also a solution to the recurrence relation.
The general solution is then
𝑎𝑛 = 𝐴 × 3𝑛 + 𝐵𝑛 × 3𝑛
In general, we can show that if there is only one root (in reality two repeated roots) 𝑚 of the auxiliary
equation, the general equation is then:
𝑎𝑛 = 𝐴𝑚𝑛 + 𝐵𝑛𝑚𝑛 = (𝐴 + 𝐵𝑛)𝑚𝑛
In our example above, the general solution is 𝑎𝑛 = (𝐴 + 𝐵𝑛)3𝑛.
We will use a second example to help illustrate how to solve recurrence relations when there are no real
roots. If we consider finding the general solution 𝑎𝑛 = −3𝑎𝑛−2, 𝑛 ≥ 2and then the particular solution when
𝑎0 = 1 and 𝑎1 = 2. The characteristic equation is 𝑡2 = −4which has complex solutions 𝑚 = 2𝑖and 𝑚 =
−2𝑖. The general solution is then:
𝑎𝑛 = 𝐴(−2)𝑖𝑛 + 𝐵(2𝑖)𝑛
Now, as 𝑎0 = 1 and 𝑎1 = 2, 𝑎0 = 𝐴 + 𝐵 = 1and 𝑎1 = −2𝑖𝐴 + 2𝑖𝐵 = 2 ⇒ −𝐴 + 𝑏 = −𝑖. Solving these
simultaneously for 𝐴and 𝐵 gives:
𝐴 =1
2(1 + 𝑖)
𝐵 =1
2(1 − 𝑖)

The particular solution is 𝑎𝑛 = 1
2 (1 + 𝑖)(−2𝑖)𝑛 + 1
2 (1 − 𝑖)(2𝑖)𝑛.
Extension Topic: Non-homogeneous Recurrence Relations
Non-homogeneous recurrence relations are more difficult to generally solve than that of homogeneous
relations. There is no completely systematic way to solve these but sometimes a form can be suggested.
For example, taking the recurrence relation 𝑎𝑛 + 3𝑎𝑛−1 + 2𝑎𝑛−2 = 𝑛2.
Firstly, we take the homogeneous part of the relation 𝑎𝑛 + 3𝑎𝑛−1 + 2𝑎𝑛−2 = 0 whose characteristic
equation is
𝑥2 + 3𝑥 + 2 = 0
Factorising gives:
(𝑥 + 2)(𝑥 + 1) = 0
Giving solutions 𝑥 = −1and 𝑥 = −2which are the roots of the characteristic equation. This gives us the
solution to the homogeneous part in the form
𝑎𝑛 = 𝐴(−1)𝑛 + 𝐵(−2)𝑛
This is called the general solution.
As the righthand side is a quadratic, then we can form the particular solution as
𝑎𝑛 = 𝐶𝑛2 + 𝐷𝑛 + 𝐸
Where we need to find what 𝐶, 𝐷and 𝐸are to obtain the particular solution. We may do this by substituting
this into our recurrence relation with 𝑖 = 𝑛, 𝑛 − 1, 𝑛 − 2:
(𝐶𝑛2 + 𝐷𝑛 + 𝐸) + 3(𝐶(𝑛 − 1)2 + 𝐷(𝑛 − 1) + 𝐸) + 2(𝐶(𝑛 − 2) + 𝐷(𝑛 − 2) + 𝐸) = 𝑛2
Simplifying we get:
6𝐶𝑛2 + (−14𝐶 + 6𝐷)𝑛 +(11𝐶 − 7𝐷 + 6𝐸) = 1𝑛2 + 0𝑛 + 0
We can then equate coefficients:
6𝐶 = 1, = 14𝐶 + 6𝐷 = 0, 11𝐶 − 7𝐷 + 6𝐸 = 0
Solving these three equations, we get 𝐶 =1
6 , 𝐷 =
14
36 and 𝐸 = 32/216. Hence the general solution is:
𝑎𝑛 = 1
6𝑛2 + 14
36𝑛 + 32
216+ 𝐴(−1)𝑛 + 𝐵(−2)𝑛
And finally, 𝐴and 𝐵 may be found if the initial conditions are known, as before.

Recursion in Python
In this section, we will look at the programming equivalent to recurrence relation which is recursion.
At its simplest definition, recursion recalls a function within the same function.
For example, if we take the factorial of a number, which is defined as:
𝑛! = 1 × 2 × 3 × … ×(𝑛 − 1) × 𝑛
This can be expressed as:
𝑛! = 𝑛 ×(𝑛 − 1)!
Where 1! = 1.
This can then be expressed as a recursive function:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
If we call this function, say as:
n = factorial(4)
we can then trace the function through.
In our first time through the function, we will then call
4 * factorial(3)
Then, we will need to work out what factorial(3) is. To find factorial(3) we go into the function again which
leads to the line:
3 * factorial(2)
Repeating this process we find
2 * factorial(1)
Finally factorial(1) returns 1. So, then we go back through the tree:
2 * 1
Then going back a step again
3 * 2
And back again,
4 * 3
And so, finally, factorial(4) returns 12 as its result.

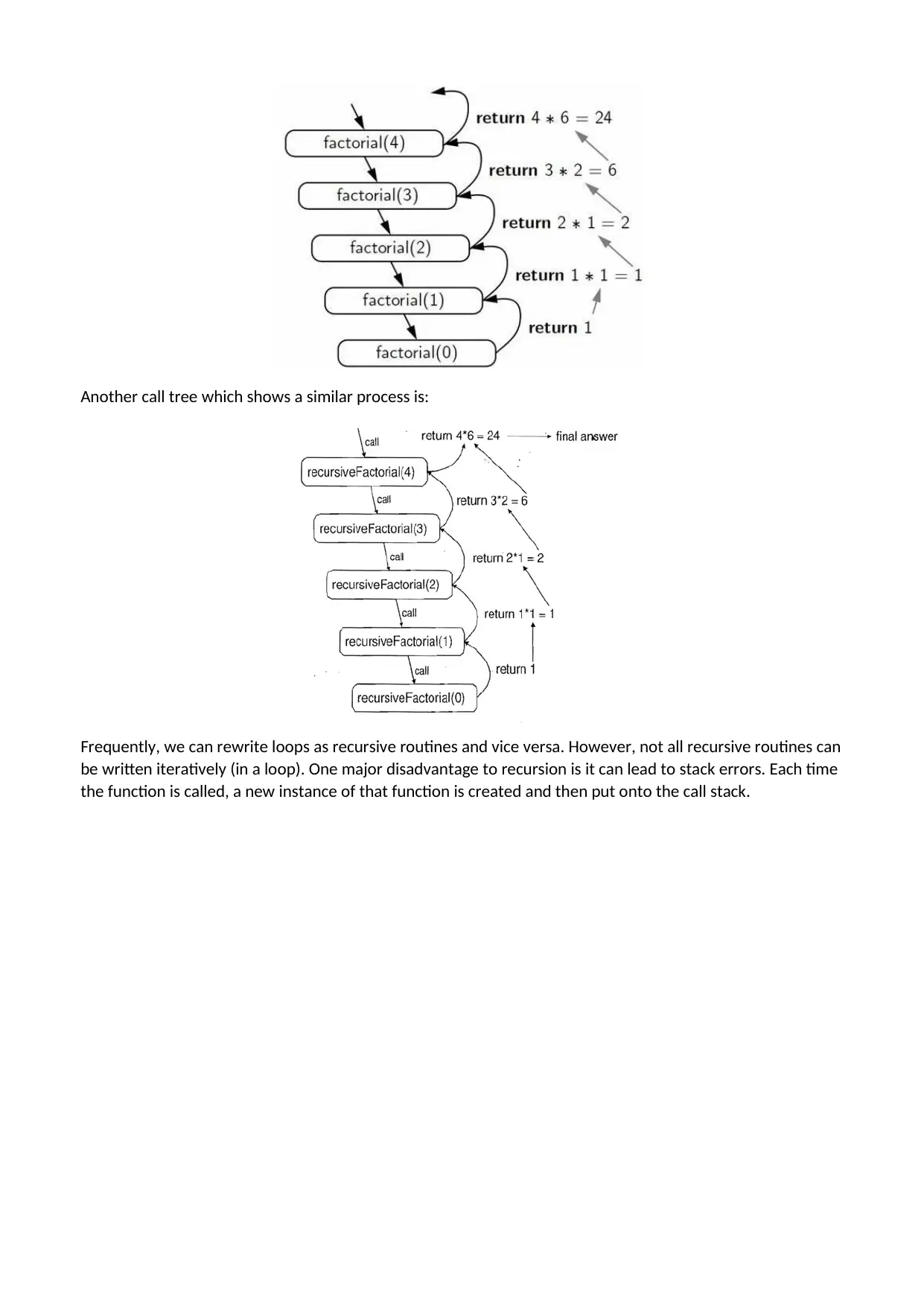
Another call tree which shows a similar process is:
Frequently, we can rewrite loops as recursive routines and vice versa. However, not all recursive routines can
be written iteratively (in a loop). One major disadvantage to recursion is it can lead to stack errors. Each time
the function is called, a new instance of that function is created and then put onto the call stack.

We therefore must ensure that we do not use recursive functions on large input variables.
Another example of a recursive function is
Which will result in the output:

By looking at the output, we can see the number is increasing by one each time through. But unlike the
factorial function there are problems with this function. The printout keeps going until the program crashes.
You might like to think about why this might happen.
The algorithm firstly prints the value of x, then increments this by one and then calls a new copy of itself with
the new value of x. This function can never terminate as there is no base condition. Before the function
terminates, another function call is made. This is an example of an infinite function.
In principle, infinite recursion is possible but not in practice. Each function call is implemented using the
system stack. A stack frame is created with space for parameters and local variables and is pushed onto the
stack. Each recursive call to the function then pushes another stack frame onto the stack. Therefore, the stack
frame increases and will grow large. Eventually the stack will grow too large, and the program will crash.
Python sets an upper limit on the number of recursive calls to a single function (which is called the depth of
recursion) so that this cannot happen.
So, the problem with the program careless is that it contains no statement that tells Python when to stop
making recursive calls to itself. It simply counts up from the starting value of x without stopping. We will need
to provide it with more information.
A possible improvement is the following:
This though will still not stop. We provided some information about when to stop but this is not acted upon
and is not used. We need an if statement that catches the stopping case (which as mentioned is called the
base case) and it makes sure that there is no recursive call to the function when that case occurs. So, we can
form the following code:

This definition ensures that there will eventually be a situation where no recursive call is made. The program
can still crash if Python’s recursion limit is exceeded though. That depends on the start and stop values that
are passed as parameters.
Instead of using an if statement for the base case, we may use an if statement for the continuation case, such
as:
This will again result in a situation where no recursive call is made.
Mathematics Questions
1) For the following recurrence relations find the order and specify whether it is homogeneous or not.
a. 𝑎𝑛 = 7𝑎𝑛−1 − 3𝑎𝑛−2
b. 𝑎𝑛 = 2𝑎𝑛−3
c. 𝑎𝑛 = 𝑛𝑎𝑛−1 + 𝑎𝑛−2
d. 𝑎𝑛 = 𝑎𝑛−1 + 𝑎𝑛−2 + 𝑛
2) What is the difference between the general solution and particular solution for a recurrence
relation?
3) For the following recurrence relations, find a closed form solution (i.e. not using recursion) by solving
the characteristic equation. Use Wolfram|Alpha Widgets: "Simultaneous Equations Solver" - Free
Mathematics Widget (wolframalpha.com) to help you solve the resulting simultaneous equations.
a) 𝑎𝑛 = 2𝑎𝑛−1 + 3𝑎𝑛−2, 𝑎0 = 1, 𝑎1 = 2
b) 𝑎𝑛 = 4𝑎𝑛−1 − 3𝑎𝑛−2 𝑎0 = 2, 𝑎1 = 5
4) Use an appropriate problem-solving strategy (such as HTTLAP from the first lecture notes) to think of
solutions to the Tower of Hanoi problem for four pegs.

Programming Questions
General
• A recursive function will have one or more parameters that are used to pass information into
the function
• The value(s) of the parameter(s) will be used to control whether or not the function calls itself
recursively (with modified parameter values)
When writing a recursive function
First identify and code the base case (the stopping case)
• All recursive functions need a base case – some have more than one
• The base case is the parameter value (or set of parameter values) for which working out the
result is a trivial task
• Example 1 Suppose we're writing a function add_all to add up all the numbers between 1 and
n. If the parameter passed as n is the number 1 the function simply returns 1
• Example 2 Suppose we're writing a function max_in to find the maximum number in a list of
numbers. If it is passed as a parameter a list containing just one number that number must be the
maximum in the list. So if the length of the list is 1 our function returns the only number in the list
Then identify and code the recursive case (the case that makes progress towards a result)
• All recursive functions need a recursive case – some have more than one
• Any parameter value for which the result cannot be found trivially must be processed using
recursion
• The recursive case is the one in which the function calls itself.
• It is needed to make progress towards a result when that result cannot be obtained in a single
step
• Each recursion involves a call to the function with parameters that are closer in value to those
that match the base case
• The function returns the result of a calculation based upon the result it gets back from the
recursive call
• Example 1 Suppose we're writing a function add_all to add up all the numbers between 1 and
n. If the parameter passed as n is the number 5 the function adds 5 to the result of adding up all
the numbers from 1 to 4
• Example 2 Suppose we're writing a functionmax_in to find the maximum number in a list of
numbers. If it is passed as a parameter a list containing several numbers the result is the larger of
the first number in the list and the maximum of thise inthe rest of the list

Example 1 add_all
def add_all (n) :
# calculates the sum of all the numbers between 1 and n if n
== 1 : # base case
return 1
else: # recursive case
total = n + add_all (n-1)
return total
Note that when add_all calls itself recursively it passes in the parameter n-1, which is 1 less than the n
it received. Thus, each recursive call makes progress towards the base case
Example 2 max_in
def max_in (numlist) :
# Finds the maximum number in a list of numbers if
len(numlist) == 1 : # base case
return numlist[0]
else: # recursive case
if numlist[0] > max_in (numlist[1:]) :
return numlist[0]
else :
return max_in (numlist[1:])
Note that when max_in calls itself recursively it passes in the parameter numlist[1:] which is one
element shorter than the list numlist that it received. Thus, each recursive call makes progress towards
the base case
Example 2a max_in but a little more efficient (and hopefully easier to read)
def max_in (numlist) :
head = numlist[0] # first number in the list
tail = numlist[1:] # rest of the list
if tail == [] : # base case (rest of list is empty)
return head
else: # recursive case
max_tail = max_in(tail)
if head > max_tail :
return head
else :
return max_tail

Use recursion to solve each of the problems below
1. Write a function that takes a positive whole number as its parameter and returns the factorial of
that number. Hint: factorial(1) is 1, factorial(n) is n*(factorial(n-1)), for all n greater than or equal
to 2
2. Write a function smallest_pos that takes a list of numbers as its parameter and returns the smallest
positive number in the list. Hint: This is like max_in, but a little more complex, because negative
numbers are not counted).
No need to worry about what to do with a list that does not contain a positive number
3. Write a function reverse, that takes a list as its parameter and returns the reversed version of the list.
Hint: A list containing a single element does not need to be reversed. Also, reversing the list involves
placing its head after its reversed tail
Note: Python's append method will not work on lists created by unwinding from recursionj What do you have to
change to make reverse work with strings as well?
4. Write a function multiply that takes two non-negative whole numbers a and b as parameters and
multiplies them together by repeated addition. Hint: if b is 0 the function will return 0. If b is greater
than 0 it will return a + multiply(a, b-1)
What do you have to change to make this function work with negative whole numbers as well as non-negative?
5. Write a function gcd that takes two positive whole numbers a and b as parameters and returns their
greatest common divisor. Hint: use Euclid's method for finding the gcd. The base case is when a is
equal to b.
6. Write a function first_n that takes a single positive whole number, n, as its parameter and
returns a list containing the first n positive numbers in ascending order.
What do you have to change to make this function return the list of the first n positive whole numbers in
descending order?
7. Write a function power that takes two positive whole numbers a and b as parameters and returns a
raised to the power b, calculated by repeated multiplication.
8. Write a function binary that takes a non-negative whole number as its parameter and creates a
string of zeros and ones representing that number in binary
9. Write a function is_palindrome that takes a character string as its parameter and returns True if that
string is a palindrome (a string that reads the same backwards as it does forwards) and False if it is
not. Hint: An empty string is a palindrome, as is a string containing just one character. A longer string
is a palindrome if its first and last characters are the same and the rest of the string is also a
palindrome.
What do you have to change to make this function capable of testing whether lists are palindromes?
10. Referring to the Tower’s of Hanoi problem from the mathematics questions, think of an
appropriate solution coded in Python using recursion to solve the puzzle. Once complete, test the
solutions using your hand solutions from earlier on.