Linear Algebra Homework Assignment Solution - University of XYZ

This Linear Algebra assignment solution covers several key concepts in linear algebra, including finding the row echelon form of a matrix, calculating determinants, and determining eigenvalues and eigenvectors. The solution begins by demonstrating how to reduce a matrix to its row echelon f...Read More

Running head: LINEAR ALGEBRA 1
Linear Algebra
Professor’s Name:
Name:
Date:

LINEAR ALGEBRA 2
Question 1
A=
[ 1 0 0 3 2 4
0 2 1 2 1 2
0 0 1 1 2 1
1 0 0 4 3 1
0 0 0 0 2 1
0 0 0 0 0 7 ]First reduce the given matrix to row echelon form using matrix transformation
To eliminate the leading coefficient of the forth row, subtract row 1 from row 4 and replace row 4 with
the difference
R4 R4 – R1
A=
[1 0 0 3 2 4
0 2 1 2 1 2
0 0 1 1 2 1
0 0 0 1 1 −3
0 0 0 0 2 1
0 0 0 0 0 7 ]The determinant of the matrix is the diagonal product of its row echelon form
Determinant = 1 ×2 ×1× 1× 2× 7=28
Determinant of A = 28
Question 2
The characteristic polynomial of B is defined as Det (B-λI) where I is the identity matrix of the same
dimension as B.
In this case, I =
[ 1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1 ] λI =
[ λ 0 0 0
0 λ 0 0
0 0 λ 0
0 0 0 λ ]

LINEAR ALGEBRA 3
B-λI =
[2 5 1 1
1 4 2 2
0 0 6 −5
0 0 2 3 ]−
[ λ 0 0 0
0 λ 0 0
0 0 λ 0
0 0 0 λ ]=
[2−λ 5 1 1
1 4− λ 2 2
0 0 6−λ −5
0 0 2 3−λ ]
To get the determinant, first convert the matrix to its row echelon form
To eliminate the leading coefficient in row 2, multiply R1 by 1
2−λ and subtract the product from R2.
Replace R2 with the difference
R2 R 2− 1
2−λ ∙ R 1
[2−λ 5 1 1
0 λ2−6 λ +3
2−λ
−2 λ+3
2−λ
−2 λ+3
2−λ
0 0 6−λ −5
0 0 2 3−λ ]
To eliminate the leading coefficient in row 4, multiply R3 by 2
6− λ and subtract the product from R4.
Replace R4 with the difference
R4R 4− 2
6−λ ∙ R 3
[ 2−λ 5 1 1
0 λ2−6 λ +3
2−λ
−2 λ+3
2−λ
−2 λ+3
2−λ
0 0 6−λ −5
0 0 0 λ2−9 λ+28
6− λ
]The determinant of the matrix is the diagonal product of its row echelon form
Determinant = 2− λ × λ2−6 λ +3
2−λ × 6− λ× λ2−9 λ +28
6− λ
¿ ( λ2−6 λ+3 ) ( λ2−9 λ+28 )
¿ λ4−15 λ3+ 85 λ2−195 λ+84

LINEAR ALGEBRA 4
Thus, the characteristic polynomial of B ¿ λ4−15 λ3+85 λ2−195 λ+84

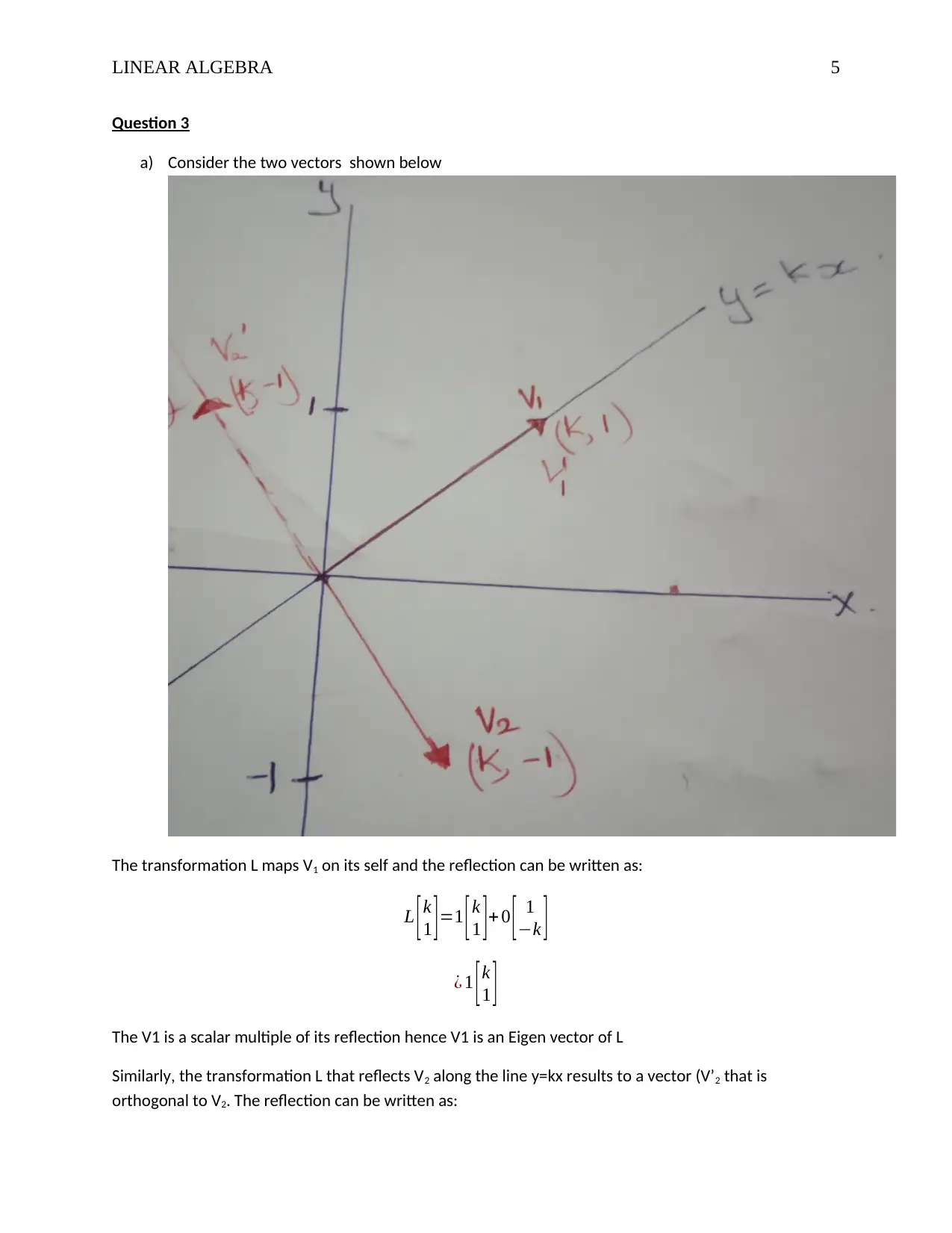
LINEAR ALGEBRA 5
Question 3
a) Consider the two vectors shown below
The transformation L maps V1 on its self and the reflection can be written as:
L [ k
1 ] =1 [ k
1 ] + 0 [ 1
−k ]
¿ 1 [k
1 ]
The V1 is a scalar multiple of its reflection hence V1 is an Eigen vector of L
Similarly, the transformation L that reflects V2 along the line y=kx results to a vector (V’2 that is
orthogonal to V2. The reflection can be written as:

LINEAR ALGEBRA 6
L [ 1
−k ]=0 [k
1 ]+−1 [−1
k ]
¿ [−1
k ]
The reflection is a scalar multiple of V2 (i.e. -1.v2) hence V2 is an Eigen vector of L.
b) The Eigen vector and Eigen values are defined as
Av=λv where A is a square matrix, v is the Eigen vector of A and λ is the Eigen value associated
with v. Thus, whenever a square matrix can be expressed as a scalar multiple of a vector, the
vector is known as the Eigen vector of the matrix and the scalar multiple is the associated Eigen
value.
From the workings in part a, the Eigen value of v1 is 1 and the Eigen value of v2 is -1
Question 4
a) A=
[2 1 −2
2 3 −4
1 1 −1 ]b) To find the Eigen values, we need to solve det (A-ΛI)=0
A=
[2 1 −2
2 3 −4
1 1 −1 ]
I = [1 0 0
0 1 0
0 0 1 ]
λI = [ λ 0 0
0 λ 0
0 0 λ ] A−λI = [2−λ 1 −2
2 3−λ −4
1 1 −1− λ ]
det (¿ A−λI )=−λ3 + 4 λ2−5 λ +2 ¿
And solving the equation −λ3+ 4 λ2−5 λ+2=0, we get λ =2 and λ= 1
Thus, the Eigen values are 1 and 2
To get the Eigen vector for λ=1
Solve: (A-ΛI) [ x
y
z ]

LINEAR ALGEBRA 7
A−λI = [2 1 −2
2 3 −4
1 1 −1 ]−1 [1 0 0
0 1 0
0 0 1 ] ¿ [1 1 −2
2 2 −4
1 1 −2 ]
Reduce the matrix to row echelon form
Swap R1 with R2
[2 2 −4
1 1 −2
1 1 −2 ]
Cancel the leading coefficient of R2 by performing R 2 R 2−1
2 R 1
[2 2 −4
0 0 0
1 1 −2 ]
Cancel the leading coefficient of R3 by performing R 3 R 3− 1
2 R 1
[2 2 −4
0 0 0
0 0 0 ]
Multiply R1 by ½ and replace it with the product
[1 1 −2
0 0 0
0 0 0 ]
The system associated with the Eigen value λ =1 is:
[1 1 −2
0 0 0
0 0 0 ][ x
y
z ]

LINEAR ALGEBRA 8
This gives the equation x=2 z− y
Thus, the Eigen vector is V = [2 z − y
y
z ]= (− y
y
0 )+
(2 z
0
z ) and y , z ≠=0
Let y =z =1
The Eigen vectors for λ = 1 are
(−1
1
0 )∧ (2
0
1 )
To get the Eigen vector for λ=2
Solve: (A-ΛI) [ x
y
z ]
A−λI = [ 2 1 −2
2 3 −4
1 1 −1 ] −2 [ 1 0 0
0 1 0
0 0 1 ] ¿ [0 1 −2
2 1 −4
1 1 −3 ]
Reduce the matrix to row echelon form
Swap R1 with R2
[2 1 −4
0 1 −2
1 1 −3 ]
Cancel the leading coefficient of R3by performing R 3 R 3− 1
2 R 1
[2 1 −4
0 1 −2
0 1
2 −1 ]
Cancel the leading coefficient of R3 by performing R 3 R 3− 1
2 R 2

LINEAR ALGEBRA 9
[2 1 −4
0 1 −2
0 0 0 ]
Cancel the leading coefficient of R1 by performing R 1 R 1−R 2
[2 0 −2
0 1 −2
0 0 0 ]
Multiply R1 by ½ and replace it with the product
[1 0 −1
0 1 −2
0 0 0 ]
The system associated with the Eigen value λ =2 is:
[1 0 −1
0 1 −2
0 0 0 ][ x
y
z ]
This gives the equations x=z andy=2 z
Thus, the Eigen vector is V = [ z
2 z
z ] z ≠=0
Let z =1
The Eigen vectors for λ = 2 is
(1
2
1 )
The Eigen values for A are λ =1 and λ=2
The Eigen vectors for A are:

LINEAR ALGEBRA 10
(
−1
1
0 ) , ( 2
0
1 ) , ( 1
2
1 )