Operations Research and Logistics: Leach Distributors Case Study
VerifiedAdded on 2023/06/09
|17
|1015
|181
Case Study
AI Summary
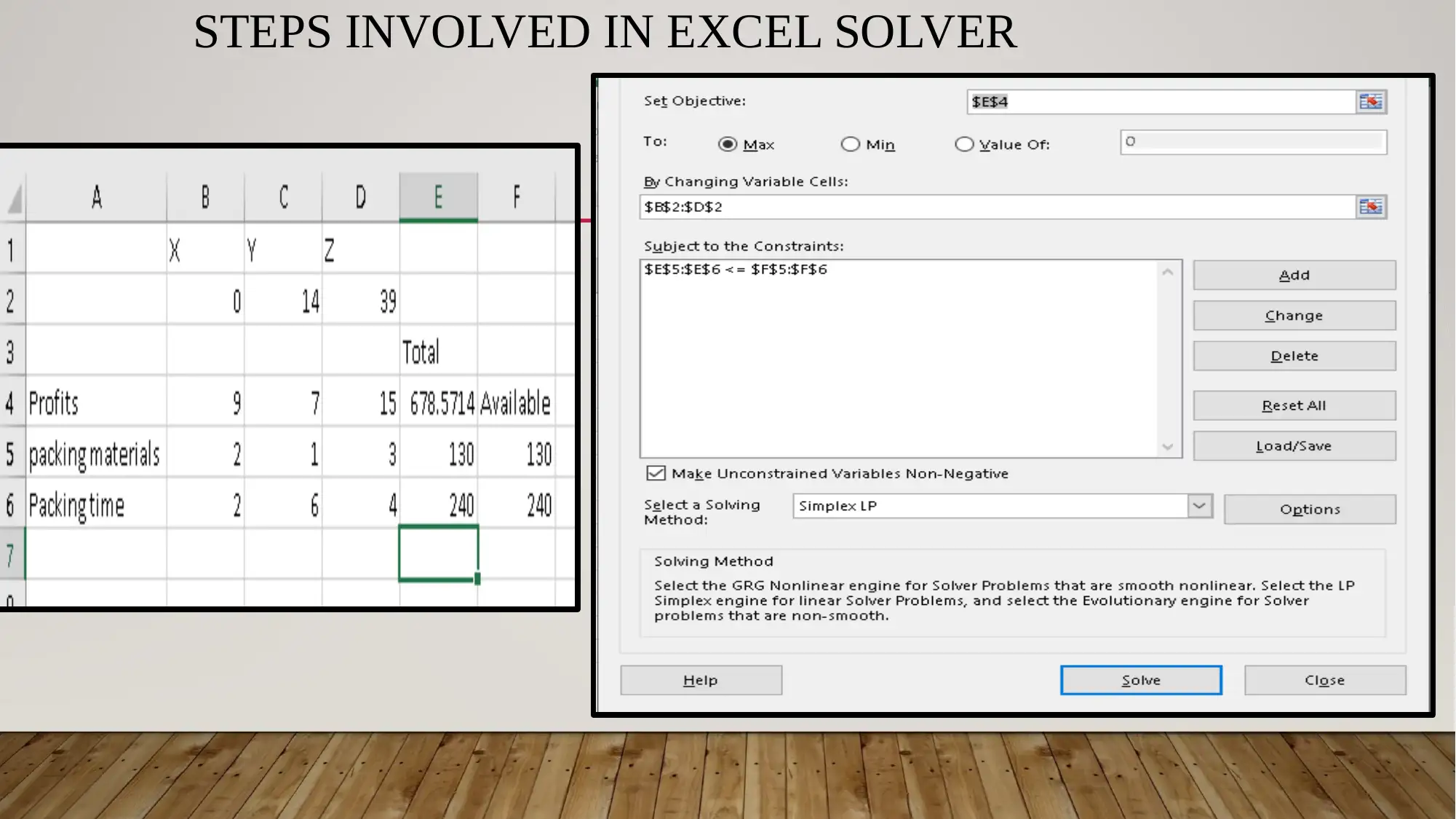
This assignment presents a comprehensive case study on Leach Distributors, focusing on the application of linear programming to optimize container usage for packaging. The student formulates the optimization problem by defining decision variables, an objective function (maximizing profit), and constraints related to packing material and time. The solution utilizes Microsoft Excel Solver to determine the optimal number of each container class (A, K, and T) to maximize profit while adhering to resource restrictions. The implications of resource constraints are analyzed, and the benefits of linear programming in a manufacturing context are discussed, highlighting its role in profit maximization, efficient resource utilization, and addressing bottlenecks. The conclusion summarizes the findings, emphasizing the optimal container quantities and the achievement of maximum profit within the given constraints. References to relevant academic sources are also provided.
1 out of 17
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)