Fall 2018 BUSA 421 Data Mining Project: Waste Disposal Solution
VerifiedAdded on 2023/05/30
|6
|1200
|53
Project
AI Summary
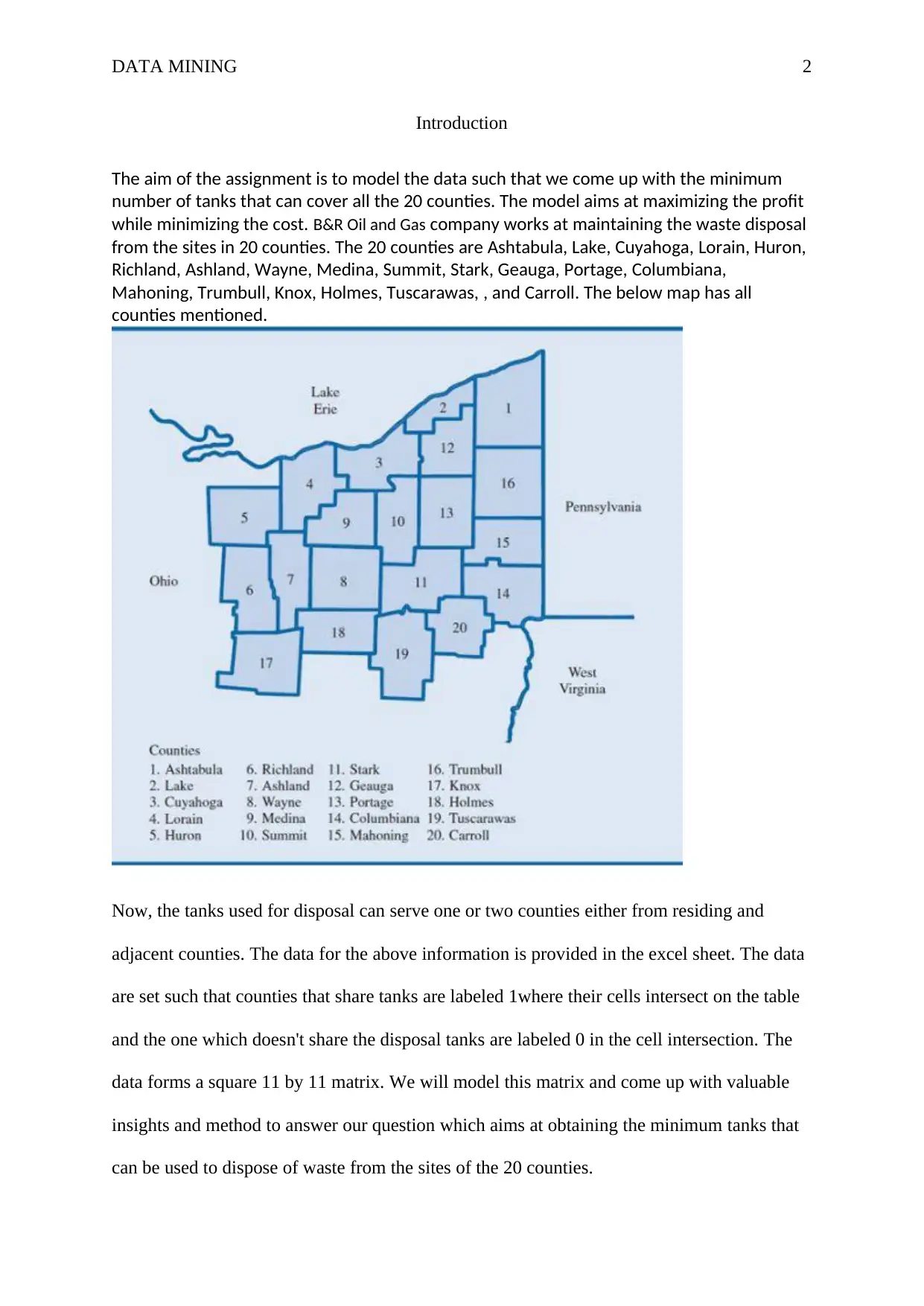
This data mining project addresses the problem of optimizing waste disposal for B&R Oil and Gas across 20 counties. The assignment's objective is to determine the minimum number of disposal tanks needed, minimizing costs and maximizing efficiency. The solution begins by identifying decision variables and objective variables, followed by creating an objective function. The project then defines constraints for each county based on adjacency and coverage. The core of the analysis employs sampling analysis, a technique used to handle large datasets. The solution models the data using a matrix and determines that a minimum of 6 tanks is required to cover all 20 counties. The project concludes by emphasizing the application of linear programming in real-world business scenarios, specifically in minimizing costs and maximizing profits. The solution includes references to relevant literature on linear programming and multi-objective decision-making.
1 out of 6







![[object Object]](/_next/static/media/star-bottom.7253800d.svg)