Linear Programming, Sensitivity Analysis, Network Modelling and Integer Linear Programming using Microsoft Excel Solver

This text explains Linear Programming, Sensitivity Analysis, Network Modelling and Integer Linear Programming using Microsoft Excel Solver with solved examples and explanations. It also covers inventory management and optimization techniques. The text includes LPP formulation, spreadsheet model, optimal production plan, sensitivity report, binding constraint, degenerate solution, unique solution, and more.

Assignment: Linear Programming, Sensitivity Analysis, Network Modelling and
Integer Linear Programming (and Inventory Management) using Microsoft Excel
Solver
Name of the Student
Name of the University

Answer to question 1:
[a] LPP formulation:
Given the information, 4 types of spa tub: Aqua-Spa (or FirstSpa, or P1), Hydro-Lux
(or SecondSpa, or P2), ThirdSpa (or P3) and FourthSpa (or P4), with the production
of products P1, ..., P4 in quantities X1, ..., X4 made up of 5 components (or things) :
Component1 (pumps, or thing1), Component2 (labour, or thing2), Component3
(tubing, or thing3), Component4 (or thing4, or plastic), Component5 (or thing5, or
clips). (We will sometimes use the terms Pi and Xi interchangeably.) The profit for
each of X1, ..., X4 is c1, ..., c4 .
Therefore, the objective function will look like:
Max Z = c1x1 + c2x2 + c3x3 + c4x4
Now, c1 = 350; c2 = 300; c3 = 390; c4 = 500
Hence, the objective function becomes:
Max Z = 350x1 + 300x2 + 390x3 + 500x4
Now, the component constraints will look like:
Component 1: x1 + x2 + x3 + x4 <= 400
Component 2: 9x1 + 6x2 + 9x3 + 12x4 <= 3132
Component 3: 12x1 + 16x2 + 14x3 + 19x4 <= 5756
Component 4: 10x1 + 12x2 +18x3 + 22x4 <= 6000
Component 5: 15x1 + 13x2 + 19x3 + 18x4 <=5992
And the non negativity constraints are x1, x2, x3, x4 >= 0

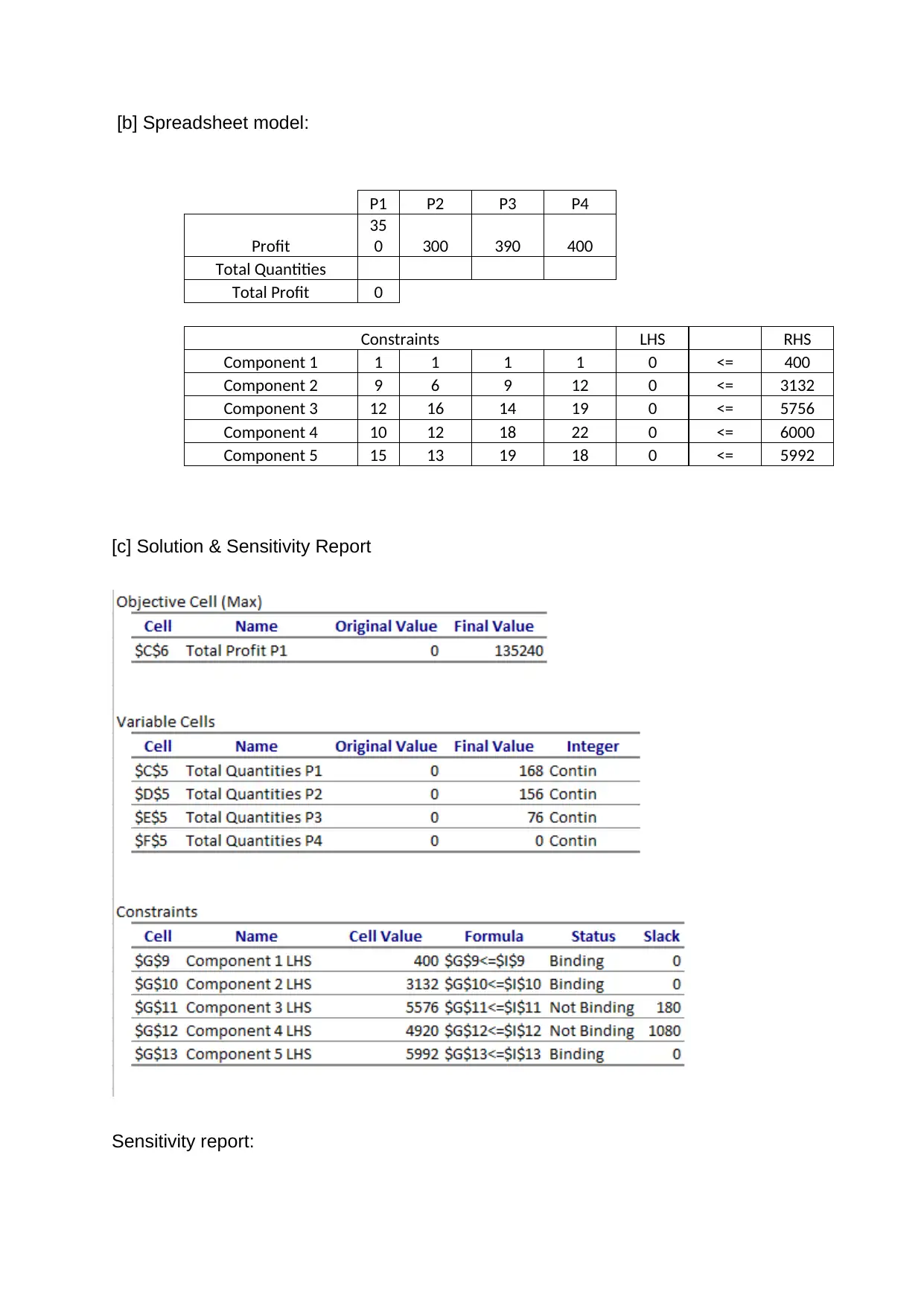
[b] Spreadsheet model:
P1 P2 P3 P4
Profit
35
0 300 390 400
Total Quantities
Total Profit 0
Constraints LHS RHS
Component 1 1 1 1 1 0 <= 400
Component 2 9 6 9 12 0 <= 3132
Component 3 12 16 14 19 0 <= 5756
Component 4 10 12 18 22 0 <= 6000
Component 5 15 13 19 18 0 <= 5992
[c] Solution & Sensitivity Report
Sensitivity report:

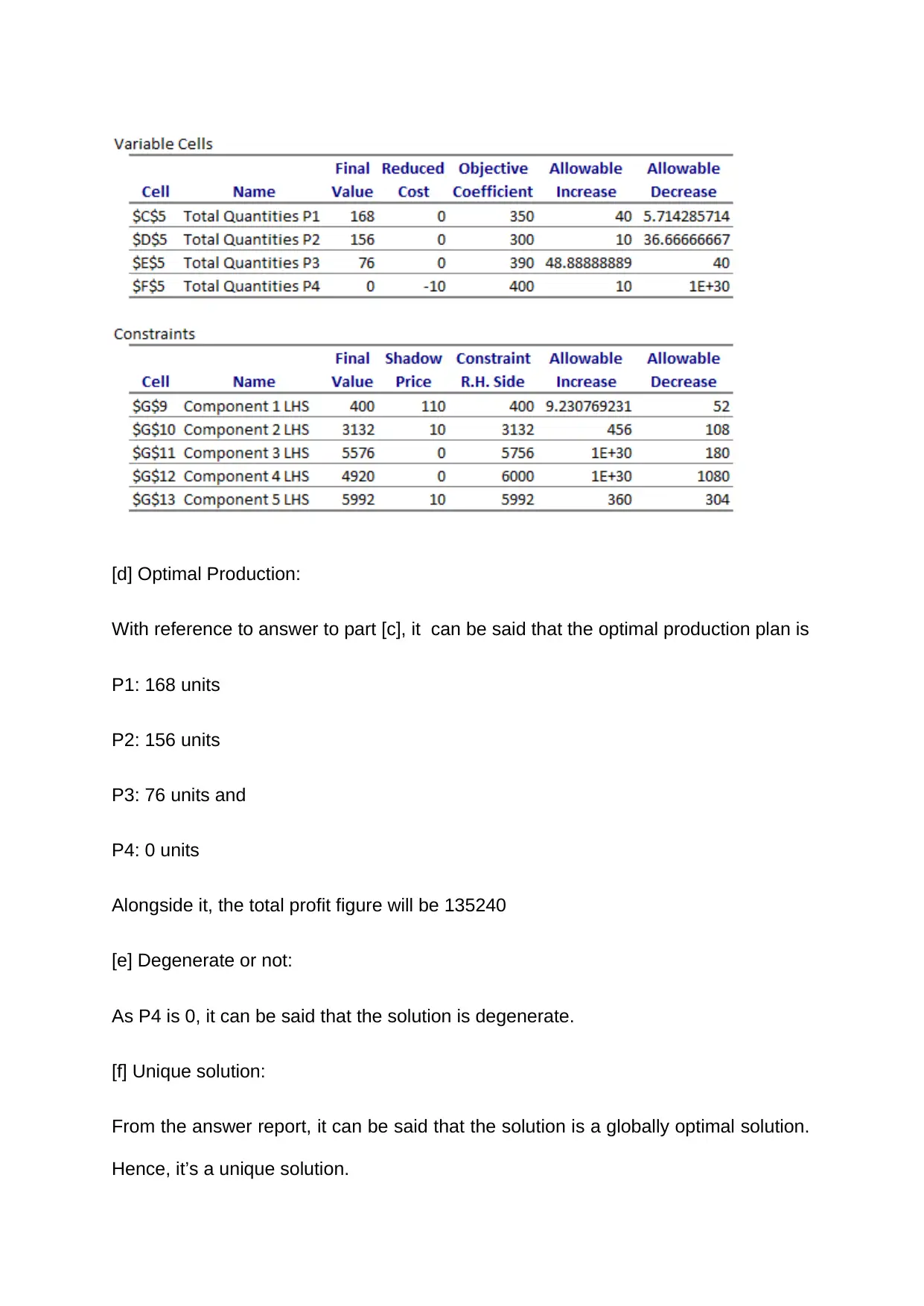
[d] Optimal Production:
With reference to answer to part [c], it can be said that the optimal production plan is
P1: 168 units
P2: 156 units
P3: 76 units and
P4: 0 units
Alongside it, the total profit figure will be 135240
[e] Degenerate or not:
As P4 is 0, it can be said that the solution is degenerate.
[f] Unique solution:
From the answer report, it can be said that the solution is a globally optimal solution.
Hence, it’s a unique solution.

[g] Binding constraint:
From the answer report, constraint table, it can be said that component 1, 2 and 5
constraints are binding constraints.
[h] Integer:
From answer report 2, it can be said that even if x1, x2, x3, and x4 becomes integer,
then also there will be no changes in xi values and thus the total profit figure.
[i] non-negative constraint:
Since, P1, P2, P3 and P4 are units, it cannot be negative. Hence, even if there is no
mention of non negativity aspect, to build the model we must have to consider x1,
x2, x3 and x4 as non negative. Or else, there will be an error in the model.
[j] change in component 1
The corresponding shadow price will tell how much the company be willing to pay for
extra pump.
For 1 pump it will be 110*1 = 110
For 100 pump it will be 110*100 = 11000, however, the organisation cannot use 100
extra pump as the max allowable increase is 9 units. It will reduce the overall profit.
[k] change in comp1,comp2 and comp5
From sensitivity report 1, we have

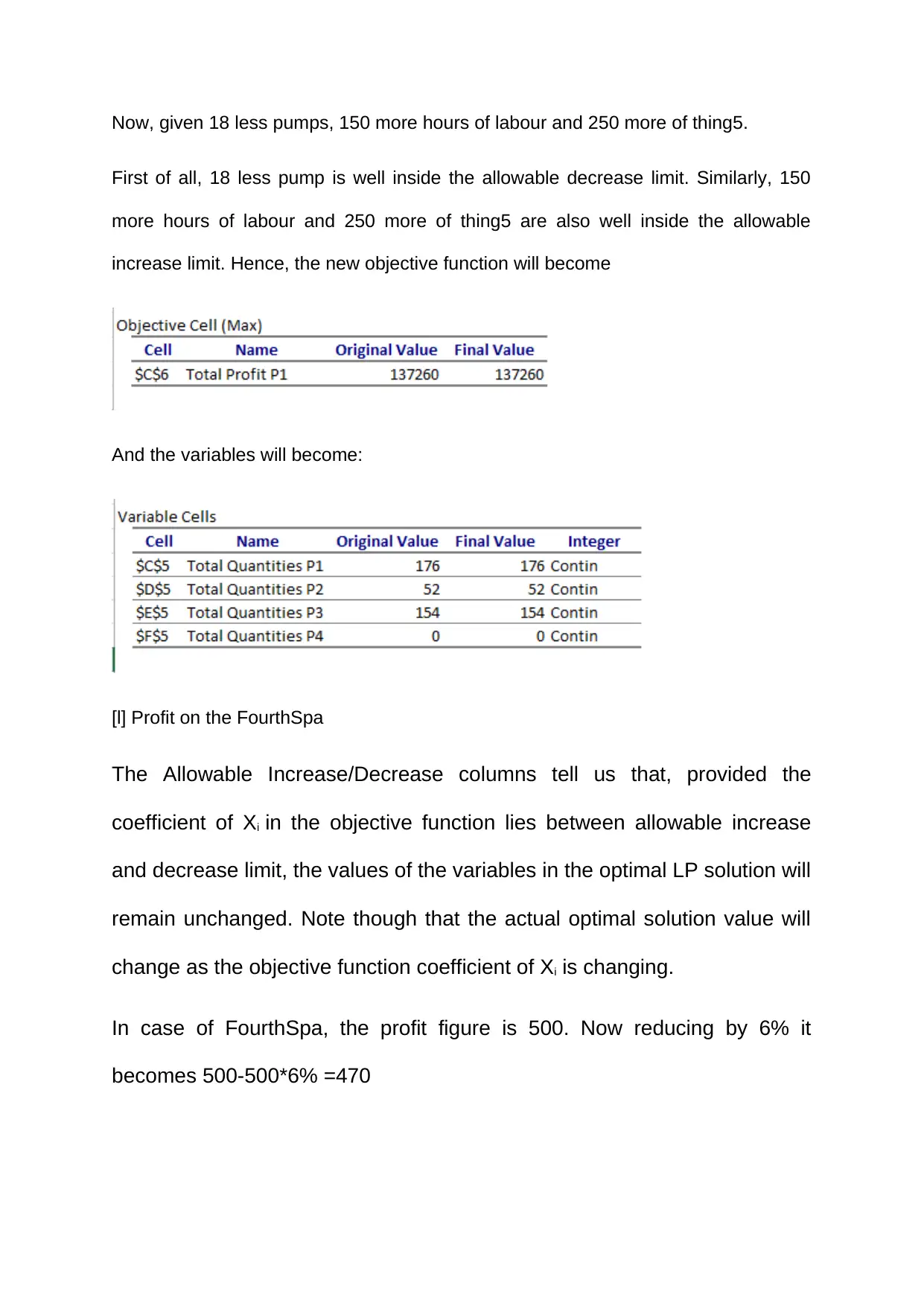
Now, given 18 less pumps, 150 more hours of labour and 250 more of thing5.
First of all, 18 less pump is well inside the allowable decrease limit. Similarly, 150
more hours of labour and 250 more of thing5 are also well inside the allowable
increase limit. Hence, the new objective function will become
And the variables will become:
[l] Profit on the FourthSpa
The Allowable Increase/Decrease columns tell us that, provided the
coefficient of Xi in the objective function lies between allowable increase
and decrease limit, the values of the variables in the optimal LP solution will
remain unchanged. Note though that the actual optimal solution value will
change as the objective function coefficient of Xi is changing.
In case of FourthSpa, the profit figure is 500. Now reducing by 6% it
becomes 500-500*6% =470

We can reduced as much as possible provided it remains the allowable
increase and decrease limit, the values of the variables in the optimal LP
solution will remain unchanged. Further, since in our optimal solution there
is no P4, there will be no change in objective function too.
[m] Added FifthSpa:
In this case, it has seen that the solution already evidenced the basis.
Hence, adding one variable will not affect the basis and thus the reduced
cost entry will be positive, which means the optimal solution will remain
same. From the sensitivity report 2, it can be said that the profit needs to
reduce by 110 so that making FifthSpa will become profitable.
[n] Three out of four Spa:
To solve this one binary constraint is added and has shown in sheet 9.
when this binary constraint is added, it can be said that there is no need of
producing SecondSpa. At the same time as FourthSpa is not producing,
the company will produce only FirstSpa and Second Spa and in such case
the profit will be 129520 [refer to answer report 5].
[o] Two out of four spa:
To solve this one binary constraint is added and has shown in sheet 14.
When this binary constraint is added, it can be said that there is no need of
producing FirstSpa and SecondSpa. The profit will become 124989.
[p] start –up cost:

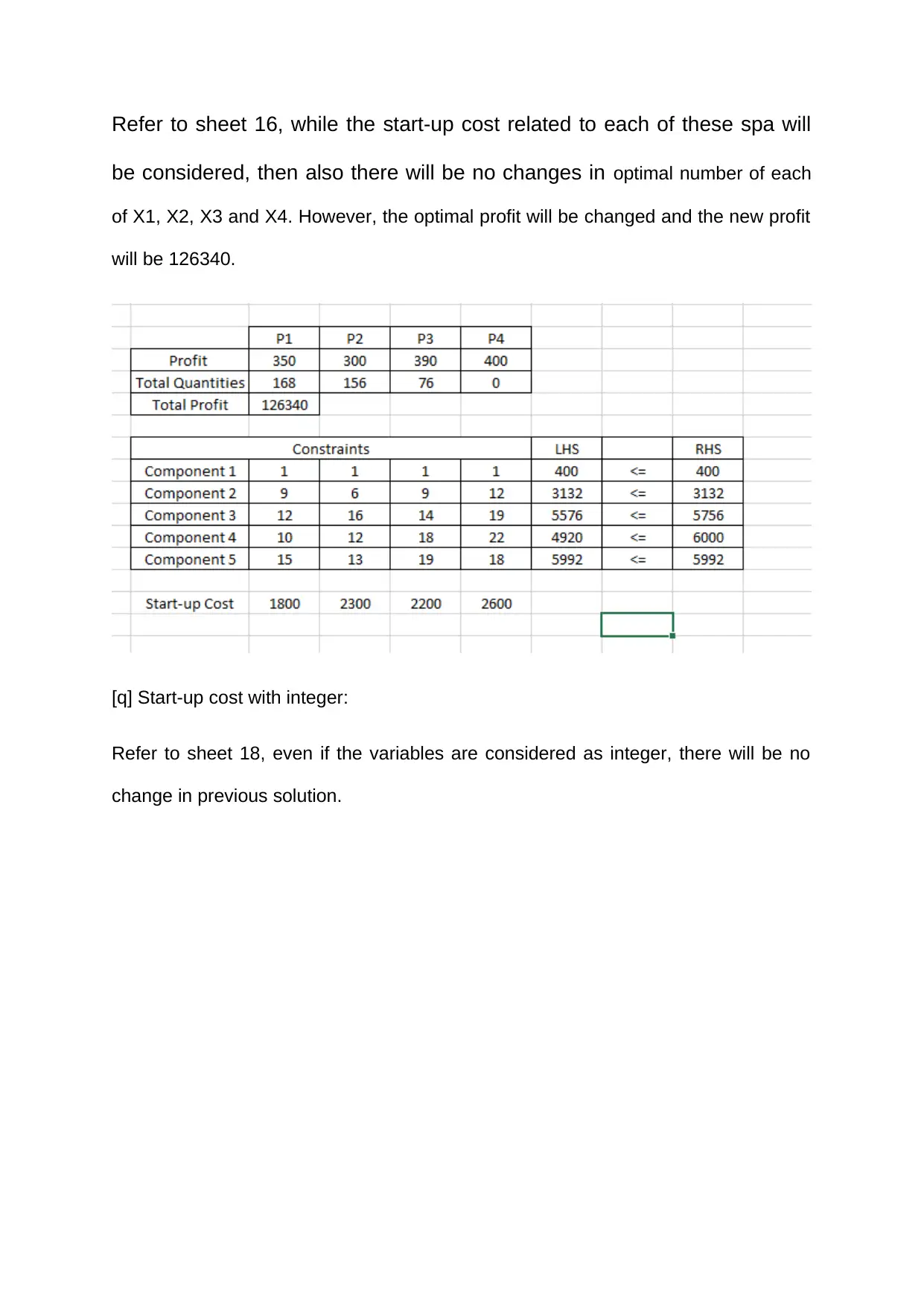
Refer to sheet 16, while the start-up cost related to each of these spa will
be considered, then also there will be no changes in optimal number of each
of X1, X2, X3 and X4. However, the optimal profit will be changed and the new profit
will be 126340.
[q] Start-up cost with integer:
Refer to sheet 18, even if the variables are considered as integer, there will be no
change in previous solution.

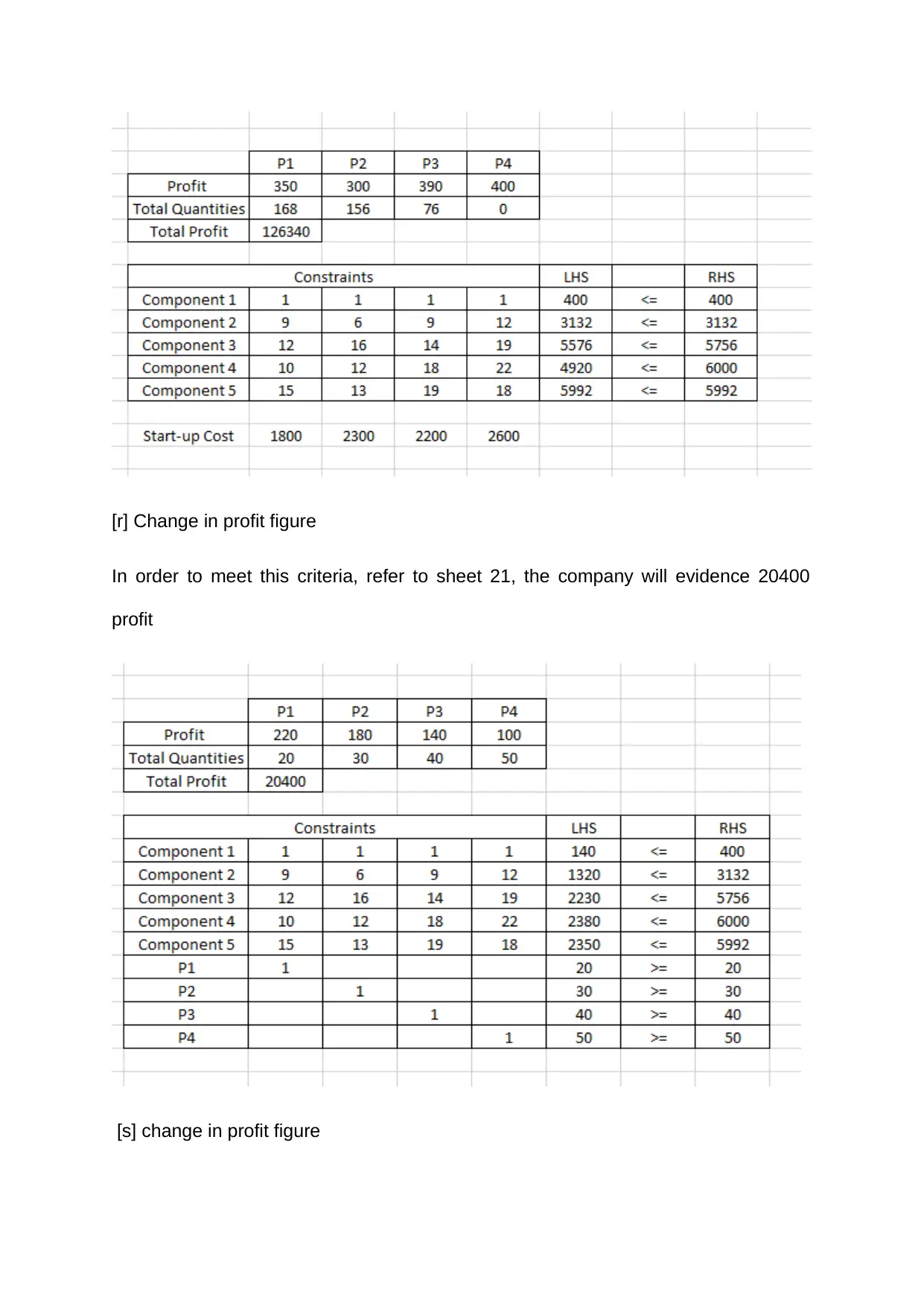
[r] Change in profit figure
In order to meet this criteria, refer to sheet 21, the company will evidence 20400
profit
[s] change in profit figure

In order to meet this criteria, refer to sheet 20, the company have to produce P1 and
P2 respectively 244 and 156 units and the total profit will be 81760.
[t] Change in profit
In order to meet this criteria, refer to sheet 20, the company have to produce P1 and
P2 respectively 244 and 156 units and the total profit will be 81760.
[u]
Answer to question 2:
[a]

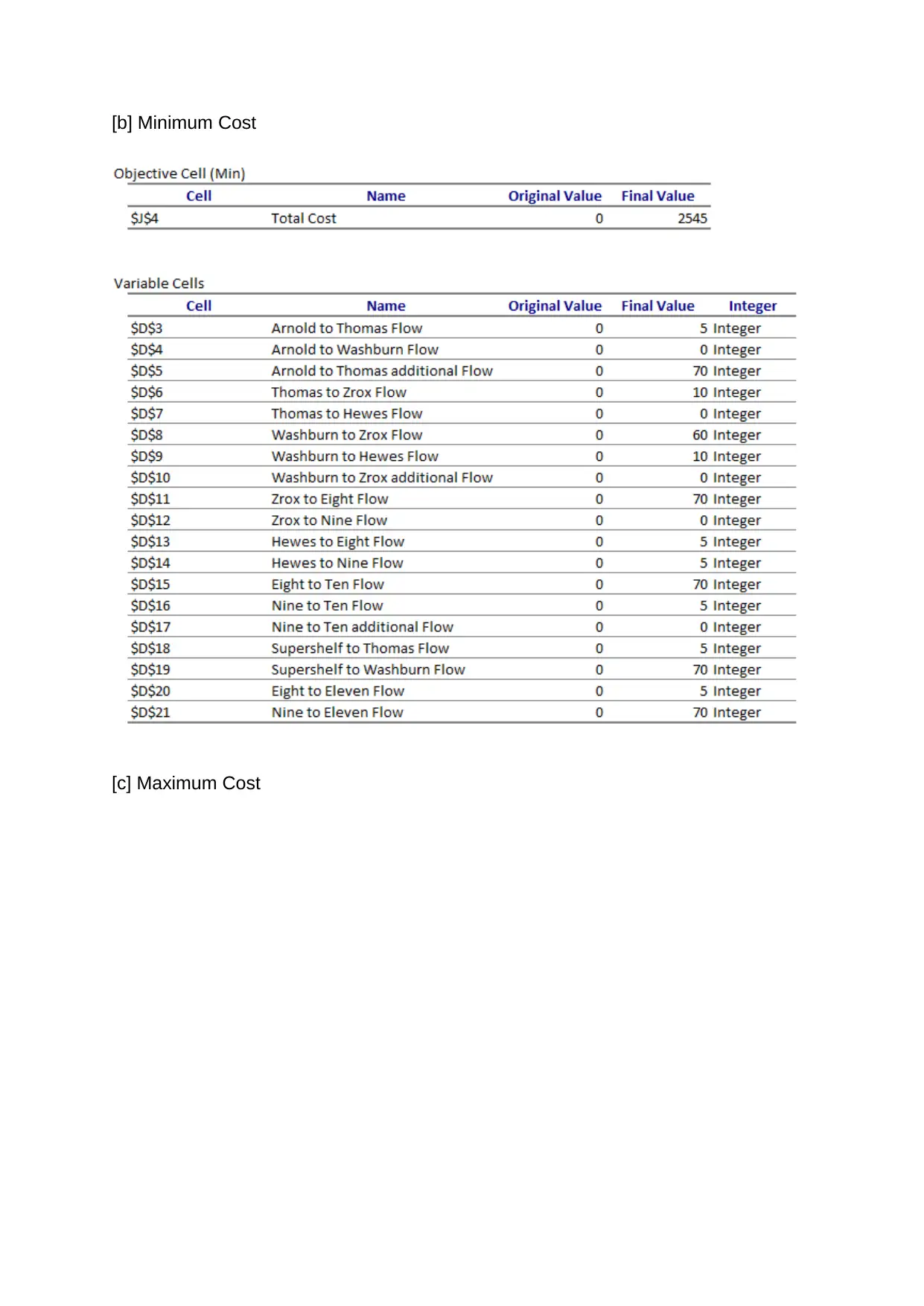
[b] Minimum Cost
[c] Maximum Cost

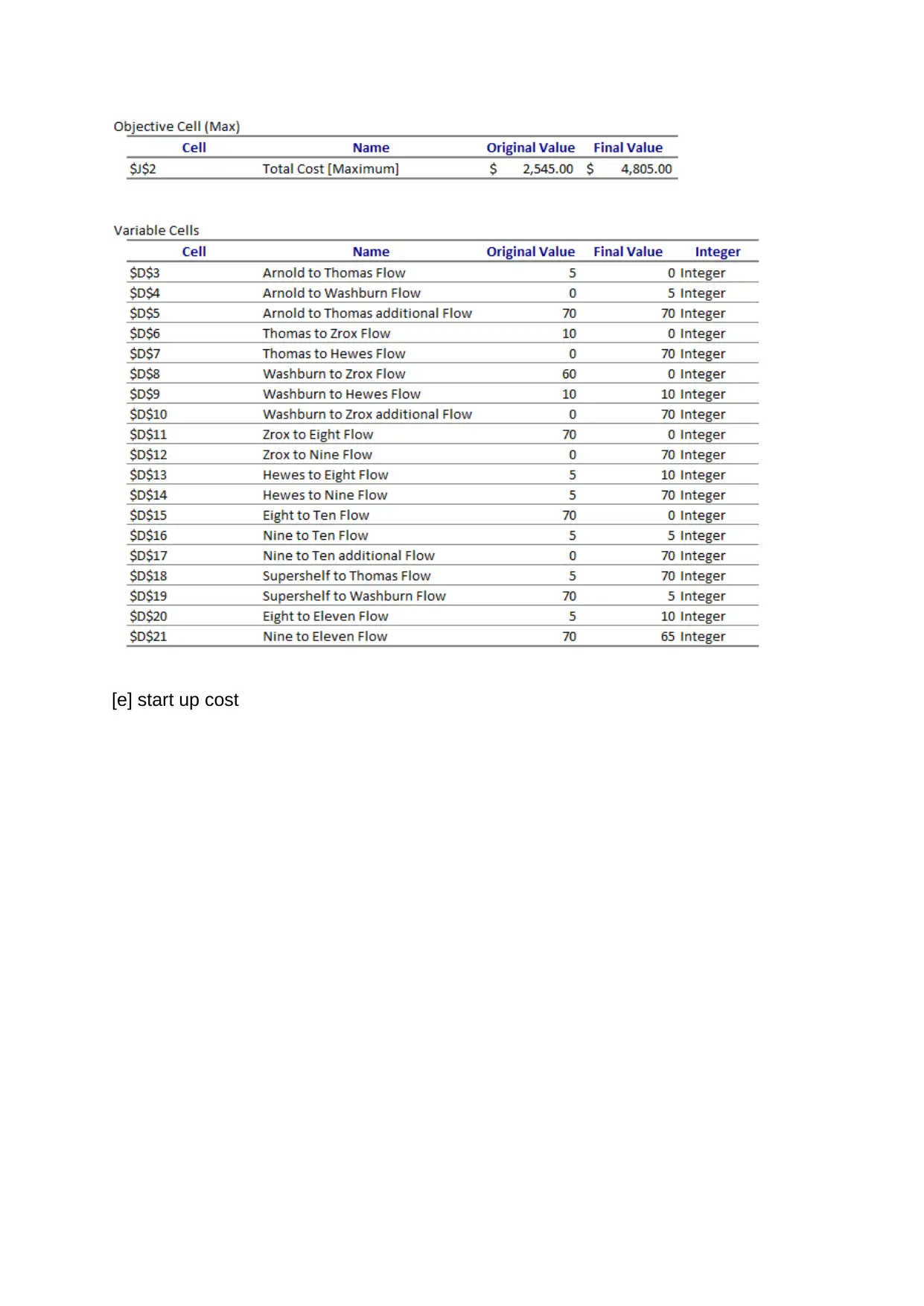
[e] start up cost

[f] Discount

[g] even number:

[h] even number:

Answer to question 3:
Part a:
Data Results
d =
4225000
0
(demand/
year)
K = $24 (setup cost)
h = $1.50
(unit holding
cost)
Annual Setup
Cost $27,577.16
Annual Holding
Cost $27,577.16
Total Variable
Cost $55,154.33
Decisio
n
Q = 36770

Part b:
Data Results
d =
4225000
0
(demand/
year)
K = $24 (setup cost)
h = $1.50
(unit holding
cost)
Annual
Setup Cost $10,140.00
Annual
Holding Cost $75,000.00
Total
Variable
Cost $85,140.00
Extra Cost $29,985.67
Decision
Q = 100000