NAME 6080 & ENMG 6150: Linear Programming Problems with Solutions
VerifiedAdded on 2023/06/09
|13
|1457
|176
Homework Assignment
AI Summary
This assignment provides solutions to several linear programming problems, employing methods like the Simplex method and graphical verification. The problems cover minimization and maximization scenarios with various constraints, including non-negative variable requirements and integer constraints. Specific questions address topics such as unbounded solutions, feasible regions, and the application of Chvatal cuts for integer programs. The solutions demonstrate the process of setting up initial tables, performing iterations, and interpreting results to find optimal solutions or identify infeasibility. The problems are relevant to courses in systems engineering and systems analysis, development, and management.

LINEAR PROGRAMMING
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question - 1
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≤ - 1
It can be written as
x1+x2 = - 1
x1 & x2 are non negative values.
Simplex Method:
Z1= x1-x2 + OS,
x1 + x2 + s1 = -1
s1 is the slack variable.
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1 -1/1 = -1
Zi 0 0 0 0
Ci - Zi 1 -1 0
Zi = ∑
i=1
1
CBi ×aij
For Minimization:
All Ci - Zi ≥ 0
Iteration 1:
Here we check the Ci - Zi value as maximum that is 1 first column. The corresponding column
value is Si = 1. This is called key column.
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≤ - 1
It can be written as
x1+x2 = - 1
x1 & x2 are non negative values.
Simplex Method:
Z1= x1-x2 + OS,
x1 + x2 + s1 = -1
s1 is the slack variable.
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1 -1/1 = -1
Zi 0 0 0 0
Ci - Zi 1 -1 0
Zi = ∑
i=1
1
CBi ×aij
For Minimization:
All Ci - Zi ≥ 0
Iteration 1:
Here we check the Ci - Zi value as maximum that is 1 first column. The corresponding column
value is Si = 1. This is called key column.

CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
Zi 1 1 1 0
Ci - Zi 0 -2 -1
The above Ci – Zi values does not satisfy minimization constraint.
All Ci - Zi ≥ 0
So, we cannot find the solution for this problem.
Question – 2
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≥ - 1
It can be written as
x1+x2 = - 1
x1 & x2 are non negative values.
Simplex Method:
Z1= x1-x2 + OS,
x1 + x2 + s1 = -1
s1 is the slack variable.
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
Zi 1 1 1 0
Ci - Zi 0 -2 -1
The above Ci – Zi values does not satisfy minimization constraint.
All Ci - Zi ≥ 0
So, we cannot find the solution for this problem.
Question – 2
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≥ - 1
It can be written as
x1+x2 = - 1
x1 & x2 are non negative values.
Simplex Method:
Z1= x1-x2 + OS,
x1 + x2 + s1 = -1
s1 is the slack variable.
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Zi 0 0 0 0
Ci - Zi 1 -1 0
Zi = ∑
i=1
1
CBi ×aij
For Minimization:
All Ci - Zi ≥ 0
Iteration 1:
Here we check the Ci - Zi value as maximum that is 1 first column. The corresponding column
value is Si = 1. This is called key column.
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
Zi 1 1 1 0
Ci - Zi 0 -2 -1
The above Ci – Zi values does not satisfy minimization constraint.
All Ci - Zi ≥ 0
So, we cannot find the solution for this problem.
Question – 3
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≥ - 1
x1 & x2 are non negative values.
Ci - Zi 1 -1 0
Zi = ∑
i=1
1
CBi ×aij
For Minimization:
All Ci - Zi ≥ 0
Iteration 1:
Here we check the Ci - Zi value as maximum that is 1 first column. The corresponding column
value is Si = 1. This is called key column.
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si 1 1 1 -1
Zi 1 1 1 0
Ci - Zi 0 -2 -1
The above Ci – Zi values does not satisfy minimization constraint.
All Ci - Zi ≥ 0
So, we cannot find the solution for this problem.
Question – 3
Minimize:
Z= x1-x2
Our Constraint is
x1+x2 ≥ - 1
x1 & x2 are non negative values.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Simplex Method:
Z1= x1-x2 + 0
x1 + x2 + s1 = -1
s1 is the slack variable.
The Constraint can be written as,
x1+x2 = - 1
x1 + x2 + s1 = -1
The constraint confliction is >=. So, the independent variables should be in negative.
-x1 - x2 - s1 = 1
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si -1 -1 -1 -1 -1
Zi 1 -1 0 0
Ci - Zi 0 0 0
The solution for this problem is unbounded.
Question – 4
Z= 10x1+x2
Our Constraint is
2x1+5x2 ≤ 11
It can be written as
2x1+5x2 = 11
Take x1=0,
2(0)+5x2 = 11
Z1= x1-x2 + 0
x1 + x2 + s1 = -1
s1 is the slack variable.
The Constraint can be written as,
x1+x2 = - 1
x1 + x2 + s1 = -1
The constraint confliction is >=. So, the independent variables should be in negative.
-x1 - x2 - s1 = 1
Initial Table:
CBi Ci 1 -1 0 Solution Rate
Basic Variable x1 x2 s1
0 Si -1 -1 -1 -1 -1
Zi 1 -1 0 0
Ci - Zi 0 0 0
The solution for this problem is unbounded.
Question – 4
Z= 10x1+x2
Our Constraint is
2x1+5x2 ≤ 11
It can be written as
2x1+5x2 = 11
Take x1=0,
2(0)+5x2 = 11
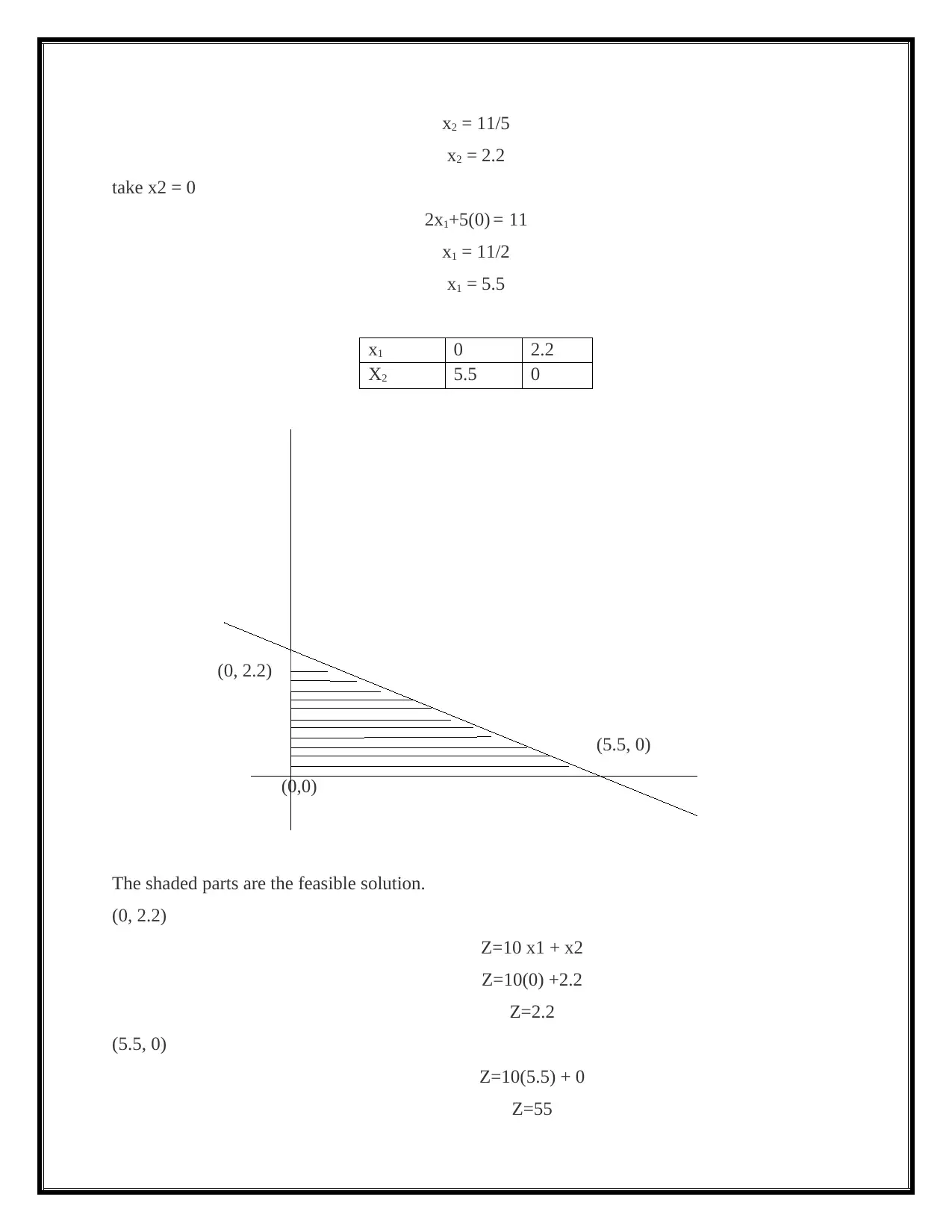
x2 = 11/5
x2 = 2.2
take x2 = 0
2x1+5(0) = 11
x1 = 11/2
x1 = 5.5
x1 0 2.2
X2 5.5 0
(0,0)
The shaded parts are the feasible solution.
(0, 2.2)
Z=10 x1 + x2
Z=10(0) +2.2
Z=2.2
(5.5, 0)
Z=10(5.5) + 0
Z=55
(5.5, 0)
(0, 2.2)
x2 = 2.2
take x2 = 0
2x1+5(0) = 11
x1 = 11/2
x1 = 5.5
x1 0 2.2
X2 5.5 0
(0,0)
The shaded parts are the feasible solution.
(0, 2.2)
Z=10 x1 + x2
Z=10(0) +2.2
Z=2.2
(5.5, 0)
Z=10(5.5) + 0
Z=55
(5.5, 0)
(0, 2.2)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

For maximization, Z=55 is the solution.
Question – 5
Maximize:
Z= 3x1+4x2
The constraints are,
2x1+x2 ≤ 6
2x1+3x2 ≤ 9
We can written as,
2x1+x2 = 6
2x1+3x2 = 9
If we take x1 = 0
2 (0) +x2 = 6
x2 = 6
If we take x2 = 0
2x1+0 = 6
x1 = 6/3
x1 =2
x1 0 3
X2 6 0
x1 = 0,
2x1+3x2 = 9
2(0) + 3x2 = 9
3x2 = 9
x2 = 9/3
x2 = 3
x2 = 0,
2x1+3x2 = 9
2 x1+ 3(0) = 9
Question – 5
Maximize:
Z= 3x1+4x2
The constraints are,
2x1+x2 ≤ 6
2x1+3x2 ≤ 9
We can written as,
2x1+x2 = 6
2x1+3x2 = 9
If we take x1 = 0
2 (0) +x2 = 6
x2 = 6
If we take x2 = 0
2x1+0 = 6
x1 = 6/3
x1 =2
x1 0 3
X2 6 0
x1 = 0,
2x1+3x2 = 9
2(0) + 3x2 = 9
3x2 = 9
x2 = 9/3
x2 = 3
x2 = 0,
2x1+3x2 = 9
2 x1+ 3(0) = 9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
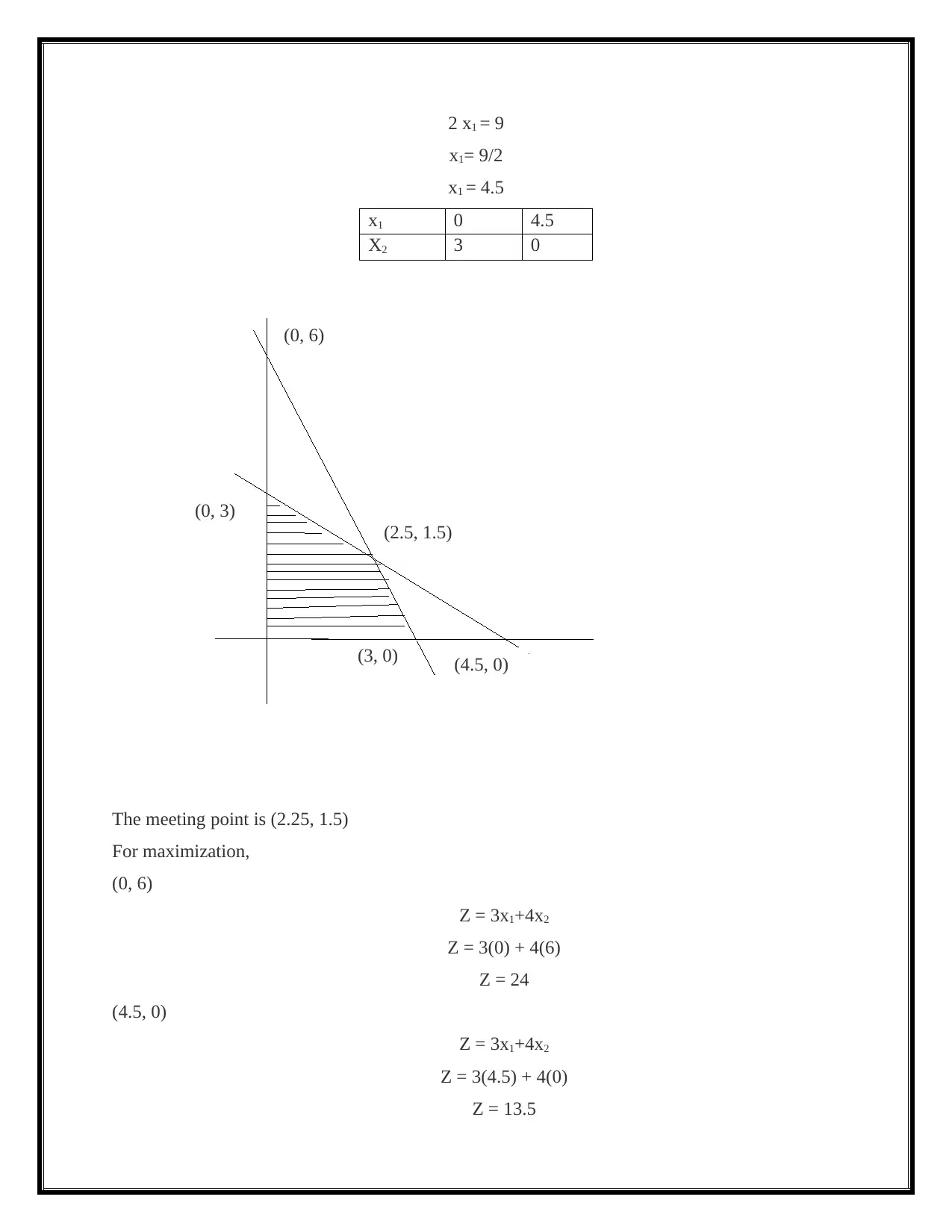
2 x1 = 9
x1= 9/2
x1 = 4.5
x1 0 4.5
X2 3 0
The meeting point is (2.25, 1.5)
For maximization,
(0, 6)
Z = 3x1+4x2
Z = 3(0) + 4(6)
Z = 24
(4.5, 0)
Z = 3x1+4x2
Z = 3(4.5) + 4(0)
Z = 13.5
(0, 3)
(2.5, 1.5)
(3, 0) (4.5, 0)
(0, 6)
x1= 9/2
x1 = 4.5
x1 0 4.5
X2 3 0
The meeting point is (2.25, 1.5)
For maximization,
(0, 6)
Z = 3x1+4x2
Z = 3(0) + 4(6)
Z = 24
(4.5, 0)
Z = 3x1+4x2
Z = 3(4.5) + 4(0)
Z = 13.5
(0, 3)
(2.5, 1.5)
(3, 0) (4.5, 0)
(0, 6)

(2.25, 1.5)
Z = 3x1+4x2
Z = 3(2.25) + 4(1.5)
Z = 12.75
The solution is (0,6).
The shaded parts of the graph is feasible solution.
Question 6
Maximize: z = x (5π – x) on [0, 20]
The value of π is 3.14.
Z = x (5*3.14 – x)
Z = x (15.7 – x)
Z = 15.7x – x2
In [0, 20], the value of x is 0,
Z = 15.7 (0) – 0
Z = 0
Use the quadratic formula,
x=−b ± √ b2−4 ac
2 a
The equation is,
Z = 15.7x – x2
x=−(−15.7)± √ (−15.7)2−4(1∗0)
2(15.7)
x= 1± √1
31.4
x= 1+ 1
31.4
x=0.064
Z = 3x1+4x2
Z = 3(2.25) + 4(1.5)
Z = 12.75
The solution is (0,6).
The shaded parts of the graph is feasible solution.
Question 6
Maximize: z = x (5π – x) on [0, 20]
The value of π is 3.14.
Z = x (5*3.14 – x)
Z = x (15.7 – x)
Z = 15.7x – x2
In [0, 20], the value of x is 0,
Z = 15.7 (0) – 0
Z = 0
Use the quadratic formula,
x=−b ± √ b2−4 ac
2 a
The equation is,
Z = 15.7x – x2
x=−(−15.7)± √ (−15.7)2−4(1∗0)
2(15.7)
x= 1± √1
31.4
x= 1+ 1
31.4
x=0.064
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
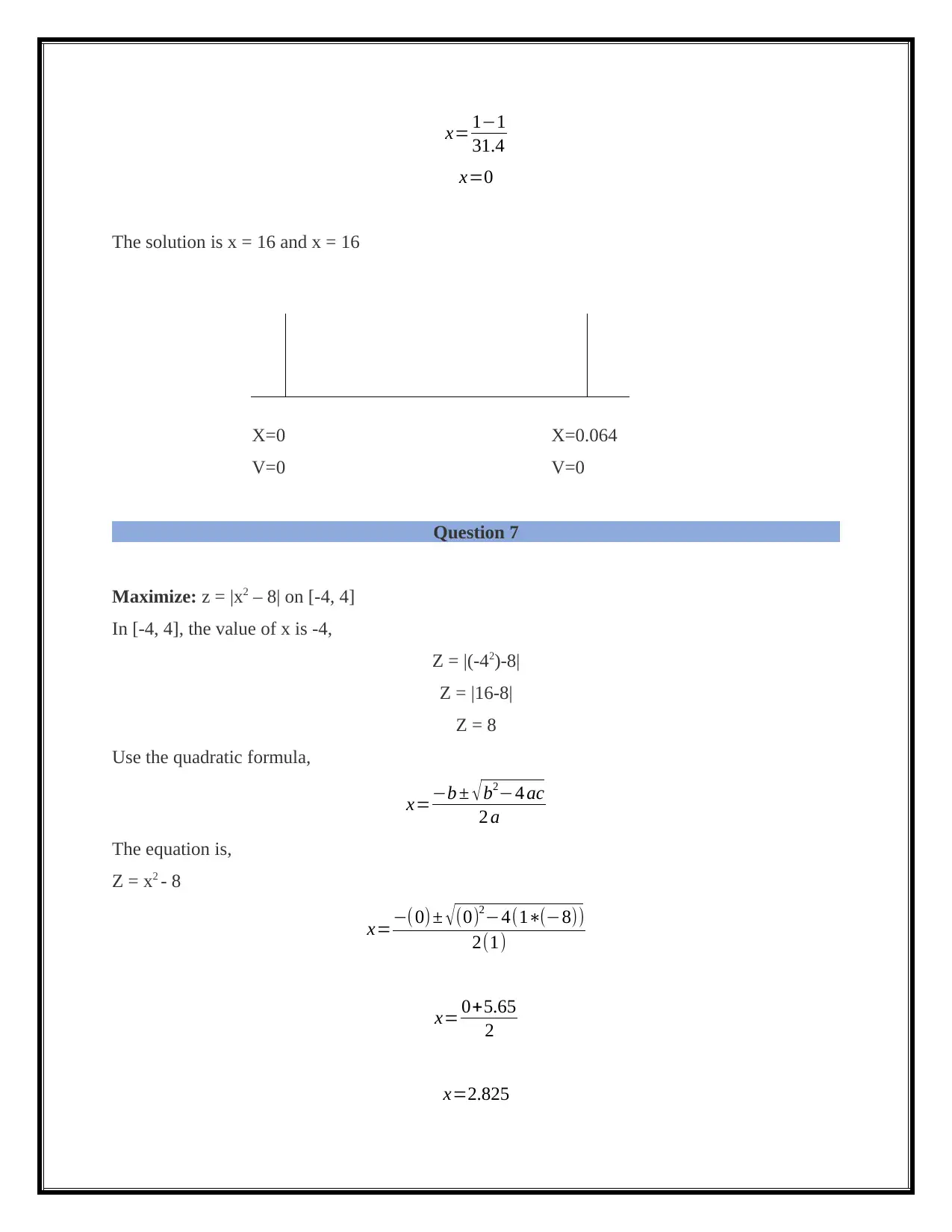
x= 1−1
31.4
x=0
The solution is x = 16 and x = 16
X=0 X=0.064
V=0 V=0
Question 7
Maximize: z = |x2 – 8| on [-4, 4]
In [-4, 4], the value of x is -4,
Z = |(-42)-8|
Z = |16-8|
Z = 8
Use the quadratic formula,
x=−b ± √ b2−4 ac
2 a
The equation is,
Z = x2 - 8
x=−(0) ± √(0)2−4(1∗(−8))
2(1)
x= 0+5.65
2
x=2.825
31.4
x=0
The solution is x = 16 and x = 16
X=0 X=0.064
V=0 V=0
Question 7
Maximize: z = |x2 – 8| on [-4, 4]
In [-4, 4], the value of x is -4,
Z = |(-42)-8|
Z = |16-8|
Z = 8
Use the quadratic formula,
x=−b ± √ b2−4 ac
2 a
The equation is,
Z = x2 - 8
x=−(0) ± √(0)2−4(1∗(−8))
2(1)
x= 0+5.65
2
x=2.825
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
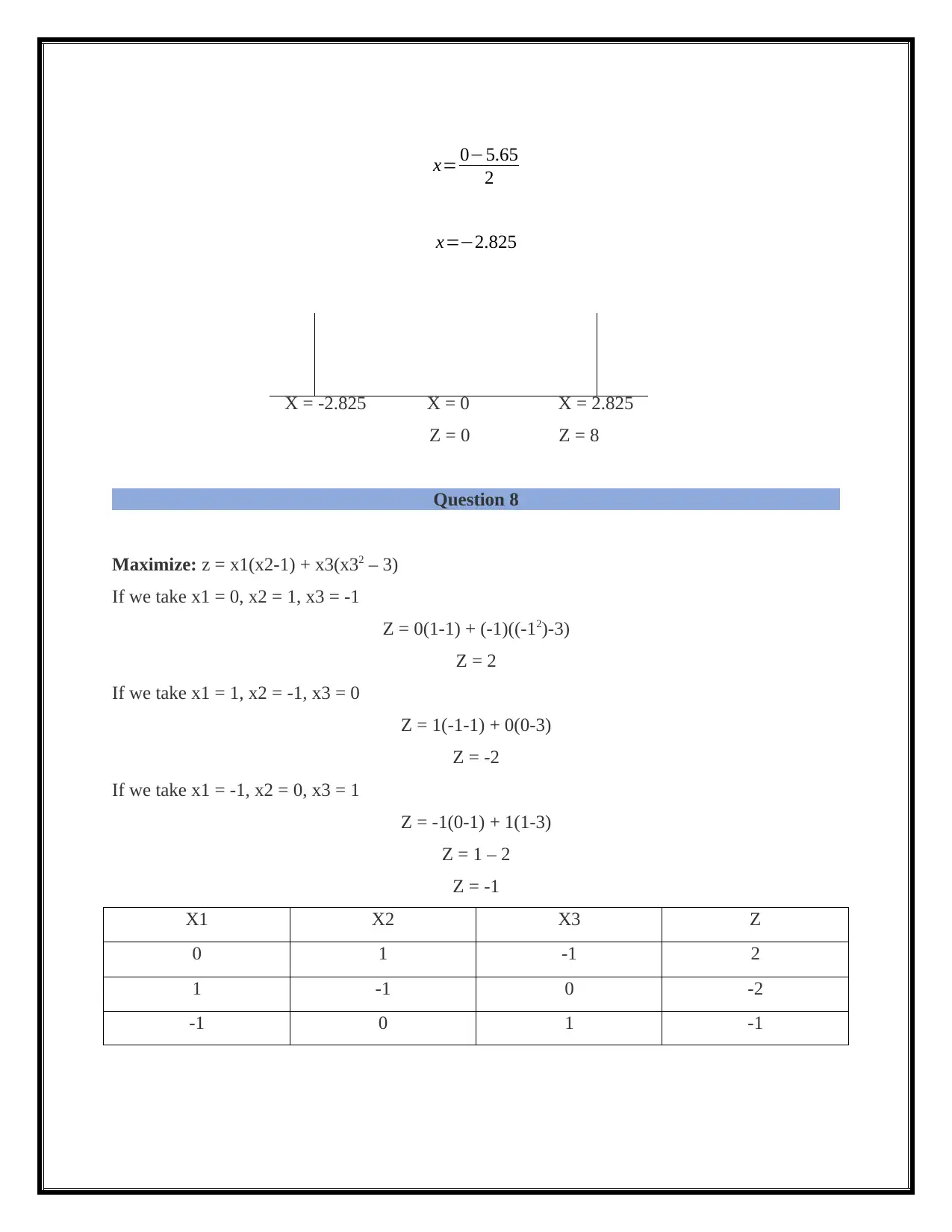
x= 0−5.65
2
x=−2.825
X = -2.825 X = 0 X = 2.825
Z = 0 Z = 8
Question 8
Maximize: z = x1(x2-1) + x3(x32 – 3)
If we take x1 = 0, x2 = 1, x3 = -1
Z = 0(1-1) + (-1)((-12)-3)
Z = 2
If we take x1 = 1, x2 = -1, x3 = 0
Z = 1(-1-1) + 0(0-3)
Z = -2
If we take x1 = -1, x2 = 0, x3 = 1
Z = -1(0-1) + 1(1-3)
Z = 1 – 2
Z = -1
X1 X2 X3 Z
0 1 -1 2
1 -1 0 -2
-1 0 1 -1
2
x=−2.825
X = -2.825 X = 0 X = 2.825
Z = 0 Z = 8
Question 8
Maximize: z = x1(x2-1) + x3(x32 – 3)
If we take x1 = 0, x2 = 1, x3 = -1
Z = 0(1-1) + (-1)((-12)-3)
Z = 2
If we take x1 = 1, x2 = -1, x3 = 0
Z = 1(-1-1) + 0(0-3)
Z = -2
If we take x1 = -1, x2 = 0, x3 = 1
Z = -1(0-1) + 1(1-3)
Z = 1 – 2
Z = -1
X1 X2 X3 Z
0 1 -1 2
1 -1 0 -2
-1 0 1 -1

Question 9
Minimize: f(x1, x2) = (x1 – 4)2 +(x2 – 4)2
The constraints are,
x1+x2 ≤ 4
x1+3x2 ≤ 9
We can written as,
x1+x2 = 4
x1+3x2 = 9
If we take x1 = 0
(0) +x2 = 4
x2 = 4
If we take x2 = 0
x1+0 = 4
x1 = 4
x1 =4
X1 0 4
X2 4 0
If we take x1 = 0
(0) +3x2 = 9
x2 = 9/3
x2 = 3
If we take x2 = 0
x1+0 = 9
x1 = 9
x1 =9
X1 0 3
X2 9 0
Minimize: f(x1, x2) = (x1 – 4)2 +(x2 – 4)2
The constraints are,
x1+x2 ≤ 4
x1+3x2 ≤ 9
We can written as,
x1+x2 = 4
x1+3x2 = 9
If we take x1 = 0
(0) +x2 = 4
x2 = 4
If we take x2 = 0
x1+0 = 4
x1 = 4
x1 =4
X1 0 4
X2 4 0
If we take x1 = 0
(0) +3x2 = 9
x2 = 9/3
x2 = 3
If we take x2 = 0
x1+0 = 9
x1 = 9
x1 =9
X1 0 3
X2 9 0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





