Control Systems: Discrete & Robust Control Solutions
VerifiedAdded on 2022/08/20
|9
|1043
|264
Homework Assignment
AI Summary
This document presents a comprehensive solution to a control systems assignment. The solution begins with the discretization of a linear system, deriving the F and Q matrices for the discrete-time state equations. It then addresses the conversion of a difference equation into a state-space representation. The core of the solution involves the design of a robust sliding mode controller for a linear time-invariant (LTI) system, including the derivation of the controller equation and simulation results using MATLAB. Finally, the assignment explores system identification techniques applied to a robotic arm modeled as a second-order system, presenting both discrete and continuous-time transfer function models derived from experimental data and system identification toolbox, along with their respective outputs. The solution demonstrates the application of various control techniques and modeling approaches.

Question 1
The linear system is given as
X ( t ) = AX ( t ) +Bu( t)
But
u ( t )=u(kT )
Hence
X ( t ) = AX ( t ) +Bu ( kT ) for kT ≤ t< ( k +1 ) T
If
A=
[1 0
0 1 ], B= [1
0 ]
From state space canonical form of a discrete system, the system is expressed in the
form of
[ x (k +1)T
x1 (k +1)T ]= [−a1 − a2
1 0 ] [ x (kT )
x1 (kT ) ]+[b
0 ]u (kT )
Where
x1 ( k ) T =x (k − 1) T
Substituting the variables in the question, we have
[ x (k +1)T
x1 (k +1)T ]= [−a1 − a2
1 0 ] [ x (kT )
x1 (kT ) ]+[b
0 ]u (kT )
[ x1 (k +1) T
x (k +1)T ]= [ 1 0
0 1 ] [ x1 (kT )
x (kT ) ] + [ b
0 ] u(kT )
x1 ( k+ 1 ) T =x1 (kT )+bu(kT )
x ( k +1 ) T =x (kT )
Which gives the difference equation shown below
x ( k +1 ) T − x (k −1)T =u (kT )
Comparing with the desired difference equation
X [ ( k +1 ) T ]=Φ ( T ) X ( kT )+φ (T ) u(kT )
From which
Φ ( T )= [0
1 ]
φ ( T ) = [ 1
0 ]
The linear system is given as
X ( t ) = AX ( t ) +Bu( t)
But
u ( t )=u(kT )
Hence
X ( t ) = AX ( t ) +Bu ( kT ) for kT ≤ t< ( k +1 ) T
If
A=
[1 0
0 1 ], B= [1
0 ]
From state space canonical form of a discrete system, the system is expressed in the
form of
[ x (k +1)T
x1 (k +1)T ]= [−a1 − a2
1 0 ] [ x (kT )
x1 (kT ) ]+[b
0 ]u (kT )
Where
x1 ( k ) T =x (k − 1) T
Substituting the variables in the question, we have
[ x (k +1)T
x1 (k +1)T ]= [−a1 − a2
1 0 ] [ x (kT )
x1 (kT ) ]+[b
0 ]u (kT )
[ x1 (k +1) T
x (k +1)T ]= [ 1 0
0 1 ] [ x1 (kT )
x (kT ) ] + [ b
0 ] u(kT )
x1 ( k+ 1 ) T =x1 (kT )+bu(kT )
x ( k +1 ) T =x (kT )
Which gives the difference equation shown below
x ( k +1 ) T − x (k −1)T =u (kT )
Comparing with the desired difference equation
X [ ( k +1 ) T ]=Φ ( T ) X ( kT )+φ (T ) u(kT )
From which
Φ ( T )= [0
1 ]
φ ( T ) = [ 1
0 ]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 2
From Real-translation, time advance property of the Z transform,
Z { x ( k +n ) T }=Zn
[ X ( z ) −∑
k=0
n −1
x (kT )Z− k
]
From the difference equation provided
c ( k +4 ) +2 c ( k +2 ) − c ( k +1 ) +c ( k )=5 u(k )
Taking Z transform on both sides and obtaining the transfer equation, we assume 0
initial conditions since no condition was provided
Z4 C ( Z ) +2 Z2 C ( Z ) − ZC ( Z ) +C ( Z ) =5 U (Z)
C ( z )
U ( z) = 5
Z 4 +2 Z2+Z +1
Using MATLAB, the system’s state space is obtained from the MATLAB script
below
z=tf('z')
NUM = [0 0 0 0 5 ]; % NUM and DEN should be same length
DEN = [1 0 2 1 1];
[A,B,C,D] = tf2ss(NUM,DEN)
z =
z
Sample time: unspecified
Discrete-time transfer function.
A =
0 -2 -1 -1
1 0 0 0
0 1 0 0
From Real-translation, time advance property of the Z transform,
Z { x ( k +n ) T }=Zn
[ X ( z ) −∑
k=0
n −1
x (kT )Z− k
]
From the difference equation provided
c ( k +4 ) +2 c ( k +2 ) − c ( k +1 ) +c ( k )=5 u(k )
Taking Z transform on both sides and obtaining the transfer equation, we assume 0
initial conditions since no condition was provided
Z4 C ( Z ) +2 Z2 C ( Z ) − ZC ( Z ) +C ( Z ) =5 U (Z)
C ( z )
U ( z) = 5
Z 4 +2 Z2+Z +1
Using MATLAB, the system’s state space is obtained from the MATLAB script
below
z=tf('z')
NUM = [0 0 0 0 5 ]; % NUM and DEN should be same length
DEN = [1 0 2 1 1];
[A,B,C,D] = tf2ss(NUM,DEN)
z =
z
Sample time: unspecified
Discrete-time transfer function.
A =
0 -2 -1 -1
1 0 0 0
0 1 0 0

0 0 1 0
B = 1
0
0
0
C = 0 0 0 5
D = 0
B = 1
0
0
0
C = 0 0 0 5
D = 0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Question 3:
Robust sliding mode controller design with λ = -5
[ x '1
x ' 2 ]= [ 0 1
− 1 2 ] [ x1
x2 ]+[0
1 ]u (t)+ [ 0
w1 ]
From the above state equations are,
˙x1=x2
˙x2=− x1 +2 x2 +u ( t ) +w1
Let the sliding variable be defined as σ .
σ =c x1 + x2 c >0
The derivative of the sliding variable with respect to time is
˙σ =c ˙x1 + ˙x2=0
˙σ = ( c +2 ) x2 − x1 +u ( t ) =0
Solving for u ( t )
ueq ( t ) =x1 − ( c +2 ) x2
So, the controller equation is
u ( t ) =ueq ( t ) − k∗sign( σ) k > 0
The initial values of c and k are chosen to be 1 and 1. By deviating p and k from their
values, the robustness is checked. This is known as parameter perturbations. A
MATLAB script is developed to simulate the system dynamics.
The script code is as shown below:
clc; clear; close all;
x1(1) = 1;
x2(1) = 1;
c = 1;
k = 1;
Ts = 0.01;
t=0: Ts:20;
w1 = 0.1*sin(cos(t));
for n=1: length(t)
sigma(n) = c*x1(n) + x2(n);
u(n) = x1(n) - (c + 2) *x2(n) - k*sign(sigma(n));
x1(n + 1) = x1(n) + Ts*x2(n);
x2(n + 1) = x2(n) + Ts*(-x1(n) + 2*x2(n) + u(n) +
w1(n));
Robust sliding mode controller design with λ = -5
[ x '1
x ' 2 ]= [ 0 1
− 1 2 ] [ x1
x2 ]+[0
1 ]u (t)+ [ 0
w1 ]
From the above state equations are,
˙x1=x2
˙x2=− x1 +2 x2 +u ( t ) +w1
Let the sliding variable be defined as σ .
σ =c x1 + x2 c >0
The derivative of the sliding variable with respect to time is
˙σ =c ˙x1 + ˙x2=0
˙σ = ( c +2 ) x2 − x1 +u ( t ) =0
Solving for u ( t )
ueq ( t ) =x1 − ( c +2 ) x2
So, the controller equation is
u ( t ) =ueq ( t ) − k∗sign( σ) k > 0
The initial values of c and k are chosen to be 1 and 1. By deviating p and k from their
values, the robustness is checked. This is known as parameter perturbations. A
MATLAB script is developed to simulate the system dynamics.
The script code is as shown below:
clc; clear; close all;
x1(1) = 1;
x2(1) = 1;
c = 1;
k = 1;
Ts = 0.01;
t=0: Ts:20;
w1 = 0.1*sin(cos(t));
for n=1: length(t)
sigma(n) = c*x1(n) + x2(n);
u(n) = x1(n) - (c + 2) *x2(n) - k*sign(sigma(n));
x1(n + 1) = x1(n) + Ts*x2(n);
x2(n + 1) = x2(n) + Ts*(-x1(n) + 2*x2(n) + u(n) +
w1(n));
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
end
figure
plot(t,x1(1:end-1));
xlabel('Time (sec)');
ylabel('x1');
title('x1 State Response');
grid
figure
plot(t,x2(1:end-1));
xlabel('Time (sec)');
ylabel('x2');
title('x2 State Response');
grid
figure
plot(t,u)
xlabel('Time (sec)');
ylabel('Input');
title('The Input');
grid
figure
plot(x1,x2);
xlabel('x1 state');
ylabel('x2 state');
title('Phase portrait');
grid
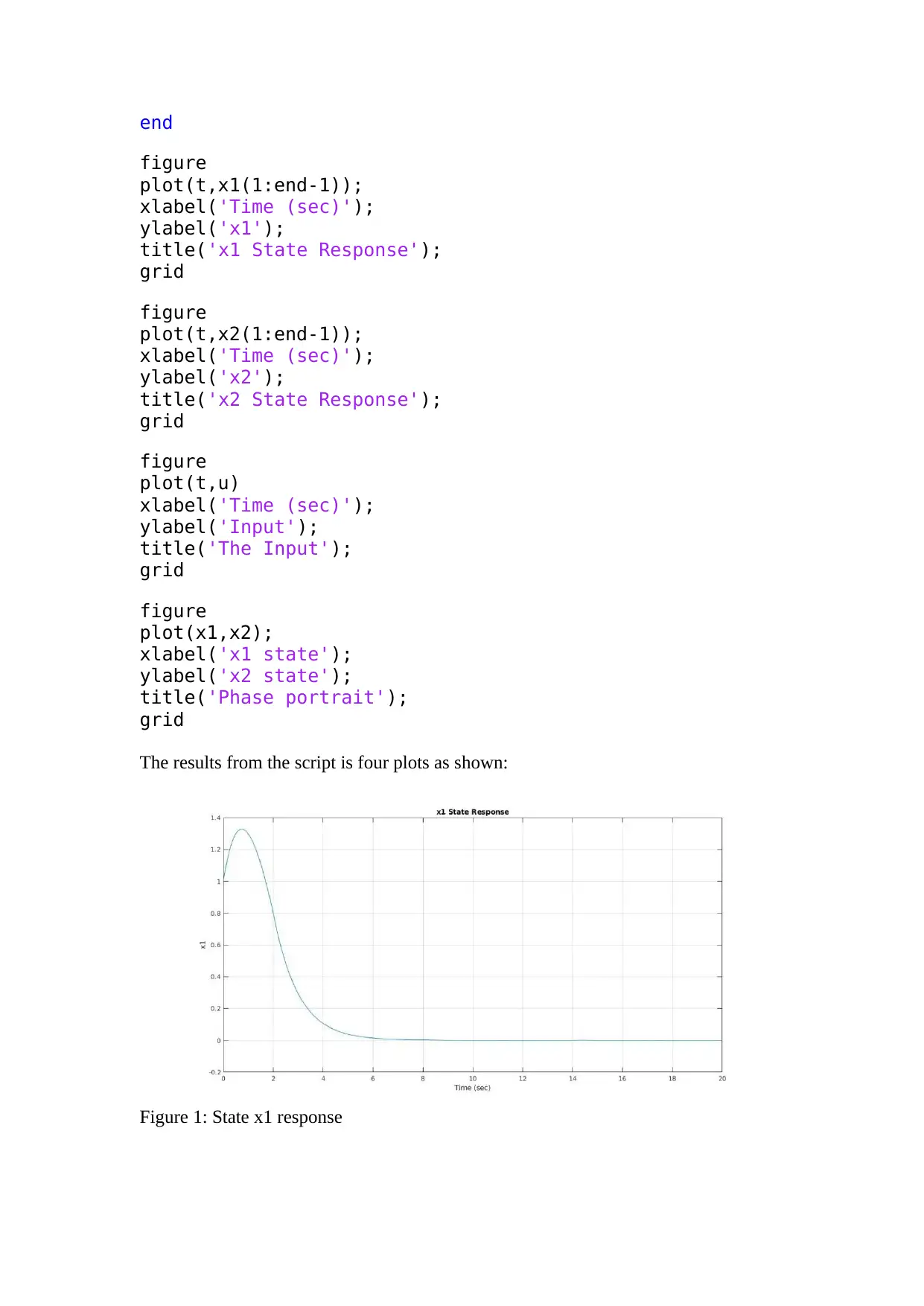
The results from the script is four plots as shown:
Figure 1: State x1 response
figure
plot(t,x1(1:end-1));
xlabel('Time (sec)');
ylabel('x1');
title('x1 State Response');
grid
figure
plot(t,x2(1:end-1));
xlabel('Time (sec)');
ylabel('x2');
title('x2 State Response');
grid
figure
plot(t,u)
xlabel('Time (sec)');
ylabel('Input');
title('The Input');
grid
figure
plot(x1,x2);
xlabel('x1 state');
ylabel('x2 state');
title('Phase portrait');
grid
The results from the script is four plots as shown:
Figure 1: State x1 response
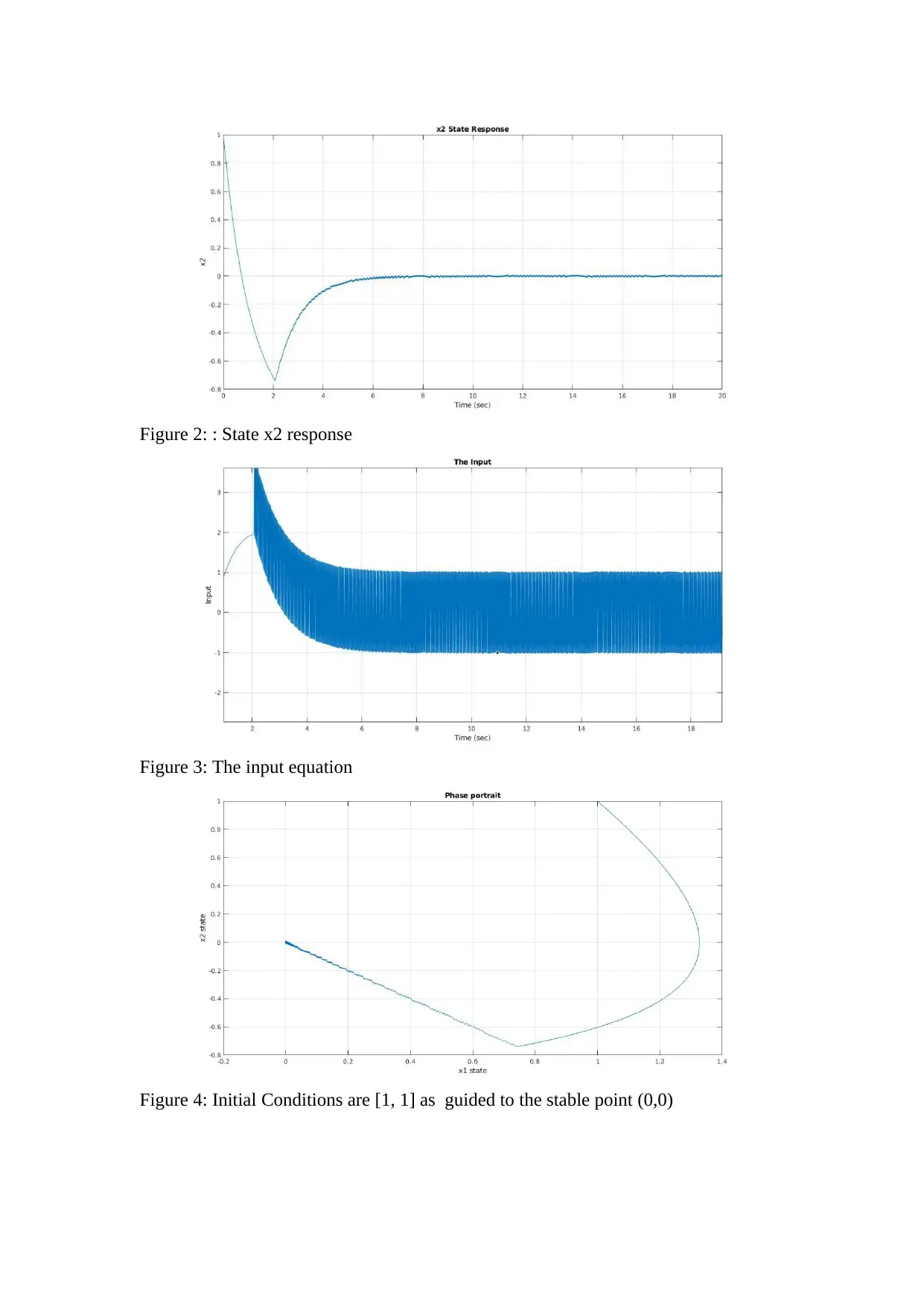
Figure 2: : State x2 response
Figure 3: The input equation
Figure 4: Initial Conditions are [1, 1] as guided to the stable point (0,0)
Figure 3: The input equation
Figure 4: Initial Conditions are [1, 1] as guided to the stable point (0,0)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Question 4:
The robotic arm is made of a dc motor. Since most motors are second order system,
the resulting model should as well be a second order. From system identification tool,
two poles (for a second order system) are and either one or none zeros in the transfer
function estimation. In state space estimation, two poles are used. In both cases, a
sampling time of 0.01 seconds is used. This is just an arbitrary value whose choice
cannot be justified.
The input and output data were plotted on the same graph to help visualize the trend.
A sampling time of 0.01 seconds was used.
Figure 5: General Visualization of the data given
From System identification, a number of models were tried and we settled on one
with four poles and three zeros. For this model, both continuous and discrete version
were evaluated.
The robotic arm is made of a dc motor. Since most motors are second order system,
the resulting model should as well be a second order. From system identification tool,
two poles (for a second order system) are and either one or none zeros in the transfer
function estimation. In state space estimation, two poles are used. In both cases, a
sampling time of 0.01 seconds is used. This is just an arbitrary value whose choice
cannot be justified.
The input and output data were plotted on the same graph to help visualize the trend.
A sampling time of 0.01 seconds was used.
Figure 5: General Visualization of the data given
From System identification, a number of models were tried and we settled on one
with four poles and three zeros. For this model, both continuous and discrete version
were evaluated.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
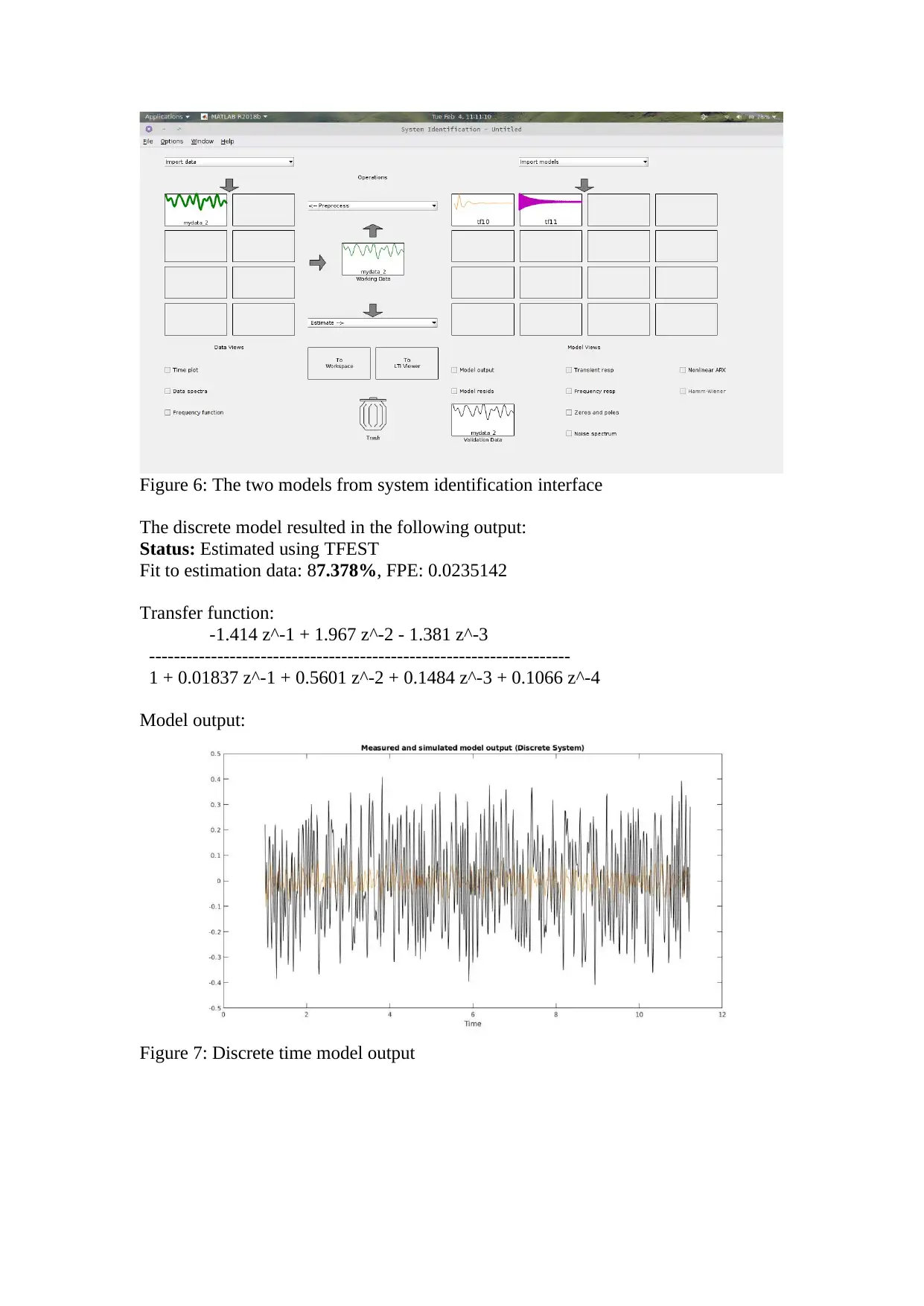
Figure 6: The two models from system identification interface
The discrete model resulted in the following output:
Status: Estimated using TFEST
Fit to estimation data: 87.378%, FPE: 0.0235142
Transfer function:
-1.414 z^-1 + 1.967 z^-2 - 1.381 z^-3
--------------------------------------------------------------------
1 + 0.01837 z^-1 + 0.5601 z^-2 + 0.1484 z^-3 + 0.1066 z^-4
Model output:
Figure 7: Discrete time model output
The discrete model resulted in the following output:
Status: Estimated using TFEST
Fit to estimation data: 87.378%, FPE: 0.0235142
Transfer function:
-1.414 z^-1 + 1.967 z^-2 - 1.381 z^-3
--------------------------------------------------------------------
1 + 0.01837 z^-1 + 0.5601 z^-2 + 0.1484 z^-3 + 0.1066 z^-4
Model output:
Figure 7: Discrete time model output
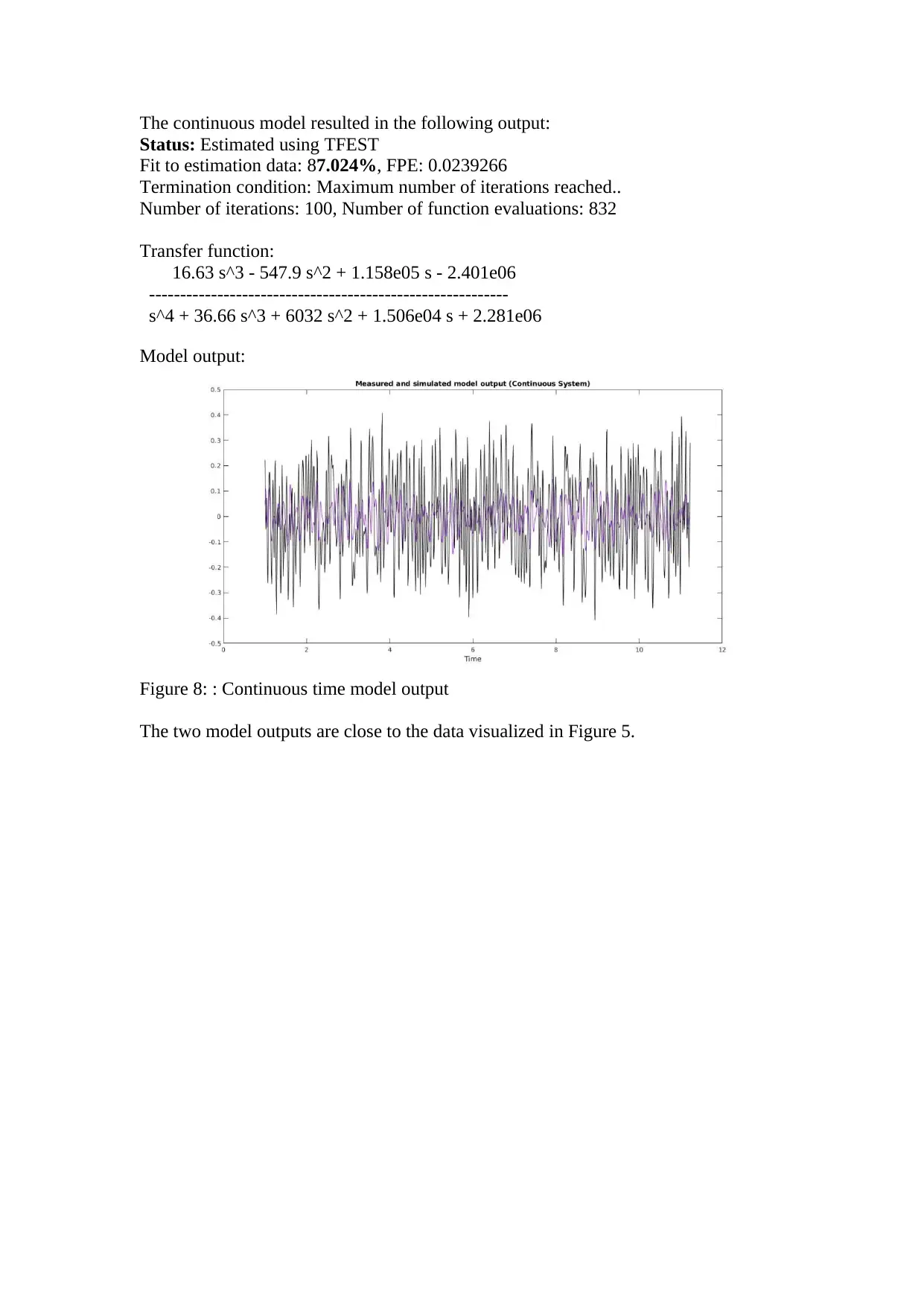
The continuous model resulted in the following output:
Status: Estimated using TFEST
Fit to estimation data: 87.024%, FPE: 0.0239266
Termination condition: Maximum number of iterations reached..
Number of iterations: 100, Number of function evaluations: 832
Transfer function:
16.63 s^3 - 547.9 s^2 + 1.158e05 s - 2.401e06
----------------------------------------------------------
s^4 + 36.66 s^3 + 6032 s^2 + 1.506e04 s + 2.281e06
Model output:
Figure 8: : Continuous time model output
The two model outputs are close to the data visualized in Figure 5.
Status: Estimated using TFEST
Fit to estimation data: 87.024%, FPE: 0.0239266
Termination condition: Maximum number of iterations reached..
Number of iterations: 100, Number of function evaluations: 832
Transfer function:
16.63 s^3 - 547.9 s^2 + 1.158e05 s - 2.401e06
----------------------------------------------------------
s^4 + 36.66 s^3 + 6032 s^2 + 1.506e04 s + 2.281e06
Model output:
Figure 8: : Continuous time model output
The two model outputs are close to the data visualized in Figure 5.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





