Relevance of Mathematical Methods in Engineering Examples

This document discusses the relevance of mathematical methods in engineering examples. It covers solving equations, analyzing geometric progressions, applying statistical techniques to interpret and present data, and using analytical and computational methods for solving problems related to sinusoidal wave and vector functions.

LO1: Identify the relevance of mathematical methods to a variety of conceptualized
engineering examples.
a. Speed dependence on pressure, density and volume is provided in the equation below. From
the [L], [M] and [T] systems, the two sides of the equations are equated to yield equation 2
shown below.
………………………..1
………………2
In order to solve for x, y and z, the corresponding polynomials of [L], [M] and [T] in the left and
right hand side of the equations are compared to obtain equations 3-5 shown below.
………………3
………………………….4
……………………………5
From equation 5,
x=−1
−2 =0.5
Substituting x=0.5 in eqn 4,
0= y +0.5
y=−0.5
From the values of x and y, substituting in eqn 1,
1=−0.5+1.5+3 z
z=0
Substituting the values of x, y and z in equation 1, we get
b. From the problem statement,
let
F α ra … … … … … … 1
F α vb … … … … … … 2
F α nc … … … … … …3
The three equations can be rewritten as equation shown in equation 4

F α ra vb nc … … … … … … 4
Using a proportionality constant k, equation 4 can be rewritten as equation 5 shown below
F=k ra vb nc … … … … … … 5
Introducing dimensional analysis on both sides of equation 4, we obtain
[ M1 L1 T 2 ]=[M 0 L1 T 0 ]a [ M 0 L1 T−2]b [M 1 L−1 T−1 ]c … … … … … … 6
Simplifying equation 5, we obtain,
[ M1 L1 T2 ]= [ M c La+b−c T−b−c ]1
… … … … … ..7
Equating the powers of L,M,T on both sides, we obtain
c=1……………8
a+b-c=1…………..9
-b-c=-2…………….10
From 8, c=1, substituting c in 10, b=-(-2+1)=1
Substituting c=1 and b=1 in equation 9, a=1
Hence
a=1, b=1, c=1
Substituting in the equation,
F=krv
c. The first term=a, d=common difference and n= number of terms
a=3
In a geometric progression, sum of nth terms Sn= n
2 (2 a+ ( n−1 ) d ) where a is the first term and d
is the common difference.
For the first 5 terms
S5=2.5(6+4d)……………1
The firs 8 terms
S8=4(6+7d)………………..2
But from the statement,
S8=2S5………………………..3
Hence 2.5 ×2(6+4d)=4(6+7d)
30+20d=24+28d…………..4
From equation 4, collecting the unknown and the known on one side, we obtain
30-24=28d-20d
Hence d=0.75
The given series =8,-4, 2, -1, +---
The common ratio r=-−4
8 =-0.5

Because r<1
Sum of nth terms,
Sn= a ( 1−r n )
1−rn
Where r ≠ 1
Sn= 8 ( 1−−0.55 )
1−−0.55 =8
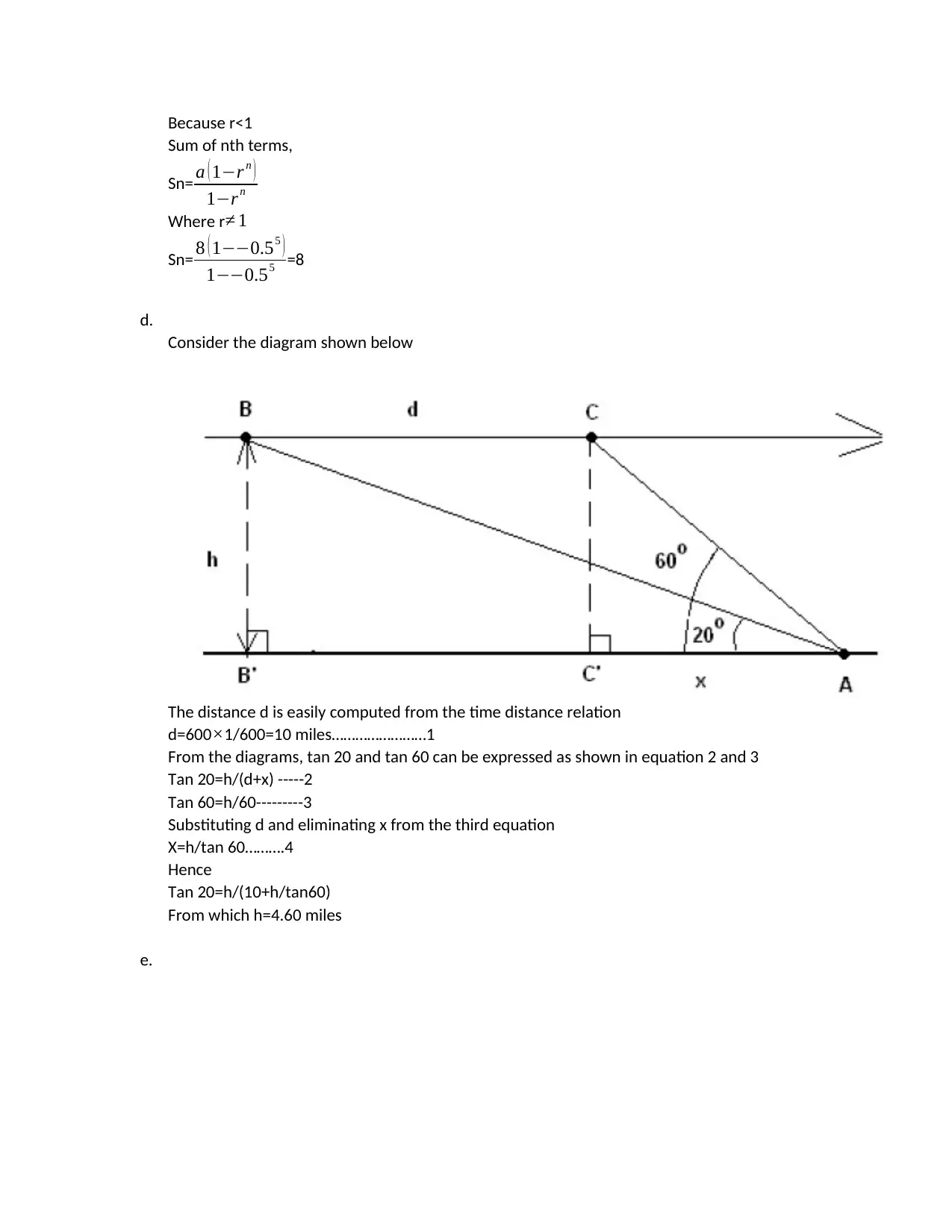
d.
Consider the diagram shown below
The distance d is easily computed from the time distance relation
d=600×1/600=10 miles……………………1
From the diagrams, tan 20 and tan 60 can be expressed as shown in equation 2 and 3
Tan 20=h/(d+x) -----2
Tan 60=h/60---------3
Substituting d and eliminating x from the third equation
X=h/tan 60……….4
Hence
Tan 20=h/(10+h/tan60)
From which h=4.60 miles
e.

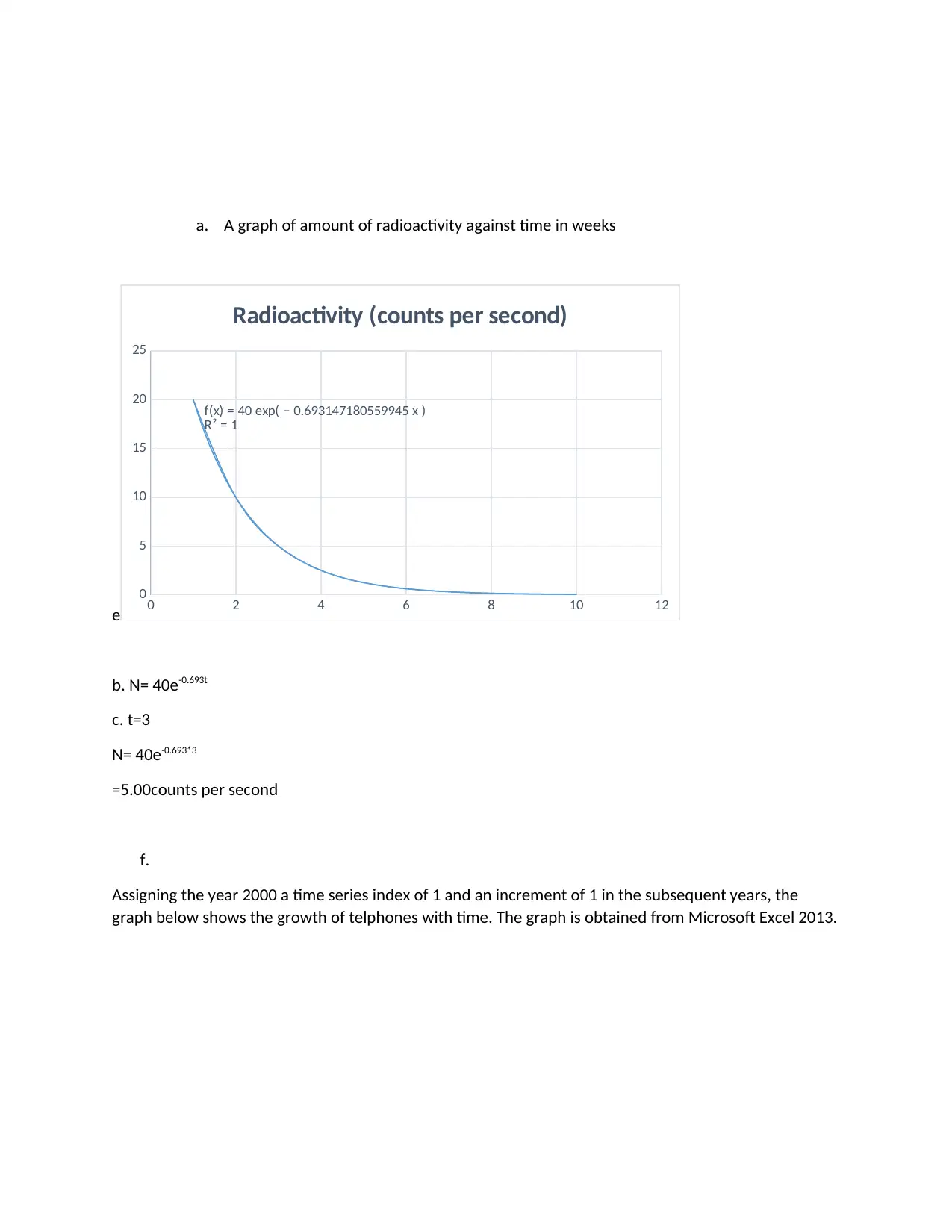
a. A graph of amount of radioactivity against time in weeks
e 0 2 4 6 8 10 12
0
5
10
15
20
25
f(x) = 40 exp( − 0.693147180559945 x )
R² = 1
Radioactivity (counts per second)
b. N= 40e-0.693t
c. t=3
N= 40e-0.693*3
=5.00counts per second
f.
Assigning the year 2000 a time series index of 1 and an increment of 1 in the subsequent years, the
graph below shows the growth of telphones with time. The graph is obtained from Microsoft Excel 2013.

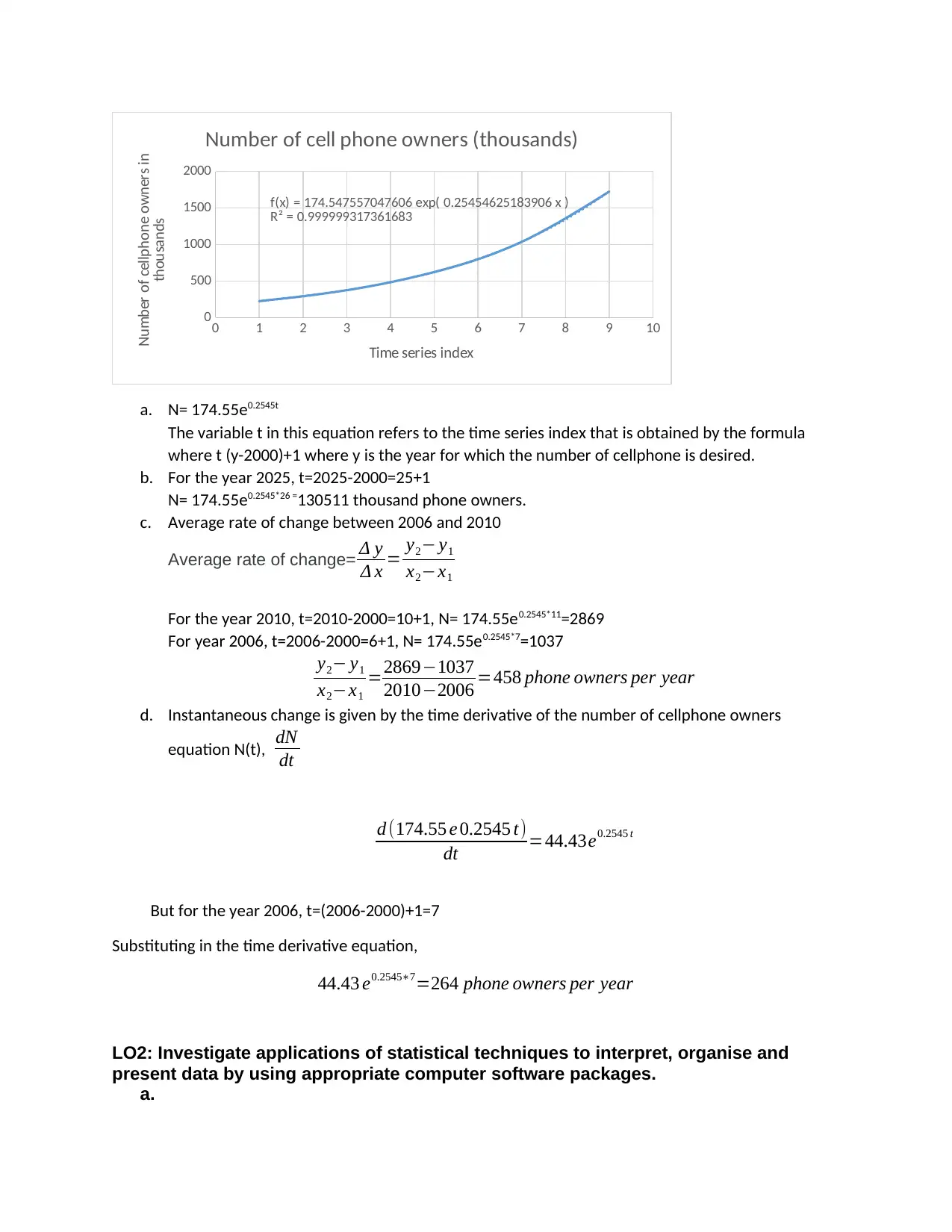
0 1 2 3 4 5 6 7 8 9 10
0
500
1000
1500
2000
f(x) = 174.547557047606 exp( 0.25454625183906 x )
R² = 0.999999317361683
Number of cell phone owners (thousands)
Time series index
Number of cellphone owners in
thousands
a. N= 174.55e0.2545t
The variable t in this equation refers to the time series index that is obtained by the formula
where t (y-2000)+1 where y is the year for which the number of cellphone is desired.
b. For the year 2025, t=2025-2000=25+1
N= 174.55e0.2545*26 =130511 thousand phone owners.
c. Average rate of change between 2006 and 2010
Average rate of change= Δ y
Δ x = y2− y1
x2−x1
For the year 2010, t=2010-2000=10+1, N= 174.55e0.2545*11=2869
For year 2006, t=2006-2000=6+1, N= 174.55e0.2545*7=1037
y2− y1
x2−x1
=2869−1037
2010−2006 =458 phone owners per year
d. Instantaneous change is given by the time derivative of the number of cellphone owners
equation N(t), dN
dt
d (174.55 e 0.2545 t)
dt =44.43e0.2545 t
But for the year 2006, t=(2006-2000)+1=7
Substituting in the time derivative equation,
44.43 e0.2545∗7=264 phone owners per year
LO2: Investigate applications of statistical techniques to interpret, organise and
present data by using appropriate computer software packages.
a.

In order to compute mean and standard deviation,
μ= ∑ x
n
And
STD= √ ( x−x)2
n−1
Using excel the columns are created as shown below
x x-mean (x-nean)^2
44 -5.2 27.04
50 0.8 0.64
38 -11.2 125.44
96 46.8 2190.24
42 -7.2 51.84
47 -2.2 4.84
40 -9.2 84.64
39 -10.2 104.04
46 -3.2 10.24
50 0.8 0.64
Sum 492 2599.6
μ= 492
10 =49.2
STD= √ (x−x)2
n−1 = √ 2599.6
10−1 =16.99542
b. Normal approximation for binomial distribution approximation is applied where continuous
distribution is employed in approximating discrete distribution. Borrowing the concept of the
Central limit theorem, sampling distribution of a mean sample if the sample size is considered to
be large enough.
In this case
p=0.25
q=1-p=0.75
np=0.25 ×20=5
nq=0.75 ×20=15>5
For normal distribution

μ=np=0.25× 20=5
5 ×0.75=3.75
,
σ = √ 3.75=1.9365
Using binomial distribution,
,
σ = √ pqn= √0.25 ×075 ×20=1.9365
In this case, binomial distribution and normal distribution gives the same values of standard deviation hence an
approximate of each other.
c. D
The mean μ=10
σ=2
Probability of replacement =3%=0.03
Z-score= x−μ
σ = x−10
2 … … … … … 1
Using the normal distribution table, we obtain
0.5-0.003=0.497
The corresponding Z-core value =-1.88
-1.88= x−10
2 ………….2
Solving for x in equation 2, we obtain guarantee period as
x=10-3.76=6.24 years
d. Letting x be the number pistons which are rejected and keeping in mind that probability success
in this case implies rejection of the pistons,
Probability variables
N=10, p=0.12, q=1-p=0.88
No piston rejected, x=0
P(x=0)=10C0(0.12)0(0.88)12=0.2785
P(x=1)=10C1(0.12)1(0.88)11=0.3798
P(x=2)=10C2(0.12)2(0.88)10=0.2330
P( x ≤ 2=0.2785+0.3798+0.2330=0.8913
Probability of at least 2 rejects
=1-P(x≤ 1¿
=1-(p(0)-(p(1)
=1-(0.2785+0.3798)
=0.3417

The lower the chances of rejection the greater the profits made by the company. The lower the
probability of pistons being rejected, the greater the profit made by the company. From the
findings of the probabilities, the probability of at least 2 pistons is rejected in less than the
probability of less than probability not more than 2 pistons being lost. This implies that more
revenue will be lost.
Standard normal scores,
Z-score= x−μ
σ
Where μ refers to the mean and σ is the standard deviation.
But μ=1000 σ =125
X=1250
1250−1000
125 =2
X=980
980−1000
125 =−0.16
X=1150
1150−1000
125 =1.2
LO3: Use analytical and computational methods for solving problems by relating
sinusoidal wave and vector functions to their respective engineering applications.
a. From the problem description, the average power
P(t)=acos(b(t-d))+C
The minimum power and maximum power p(t) from the problem statements are
Pmin=4Kwh/day
Pmax=20kwh/day
C=(Pmax+Pmin)/2= (20+4)/2=12Kwh/day
|a|=(Pmax-Pmin)/2= (20-4)/2=8Kwh/day
The number of days following the 1st of January when P(t) will be maximum is computed by
adding the days between Jan to 21st of June
t=31+28+31+30+31+21=172
Using the concept of periodic relationships in trigonometry, for (b>0)
P=365=2π/b
Hence b=2π/365

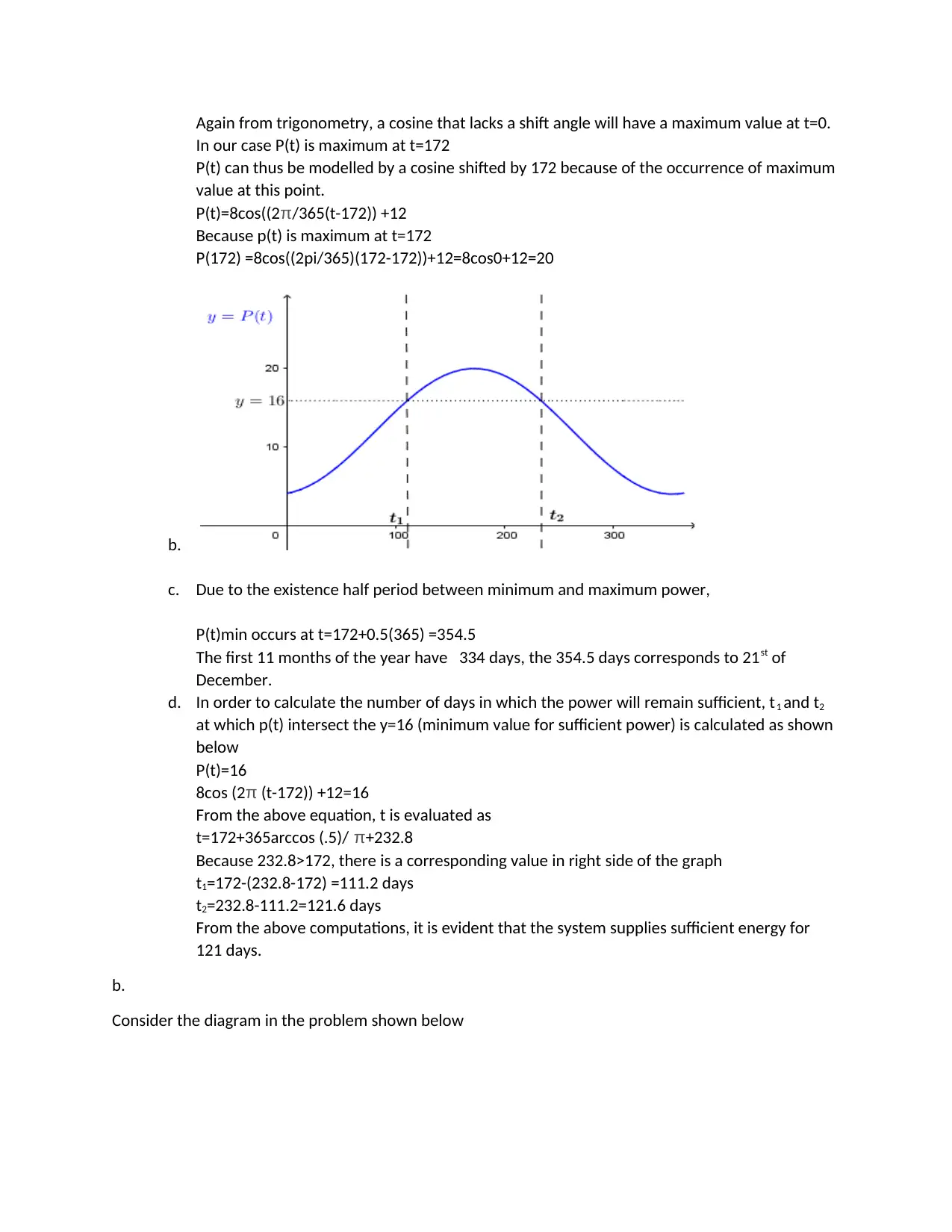
Again from trigonometry, a cosine that lacks a shift angle will have a maximum value at t=0.
In our case P(t) is maximum at t=172
P(t) can thus be modelled by a cosine shifted by 172 because of the occurrence of maximum
value at this point.
P(t)=8cos((2π/365(t-172)) +12
Because p(t) is maximum at t=172
P(172) =8cos((2pi/365)(172-172))+12=8cos0+12=20
b.
c. Due to the existence half period between minimum and maximum power,
P(t)min occurs at t=172+0.5(365) =354.5
The first 11 months of the year have 334 days, the 354.5 days corresponds to 21st of
December.
d. In order to calculate the number of days in which the power will remain sufficient, t1 and t2
at which p(t) intersect the y=16 (minimum value for sufficient power) is calculated as shown
below
P(t)=16
8cos (2π (t-172)) +12=16
From the above equation, t is evaluated as
t=172+365arccos (.5)/ π+232.8
Because 232.8>172, there is a corresponding value in right side of the graph
t1=172-(232.8-172) =111.2 days
t2=232.8-111.2=121.6 days
From the above computations, it is evident that the system supplies sufficient energy for
121 days.
b.
Consider the diagram in the problem shown below

OA=-T1cos45i+T1sin45j=T1……………..1
OB=T2cos30i+T2sin30i=T2………………..2
Substituting for cos 30 and sin30 in equations 1 and 2 and the diagram below, we obtain
T 1=−1
√2 T1 i+ 1
√2 T 1 j
T 2= √3
2 T2 i+ 1
2 T 2 j
c. The magnitude
F= √ 302 +202 +2∗20∗30 cos (150−45)
31.794 N
The phase angle = tan−1 ¿
¿
d. From the problem statement,
p=4i+0j+7k
q=-2i+j+3k
P.Q=(4 ×2)+(0×2)+(7×3)=13
By definition of a dot product
P.Q=|P.Q|cos∅

¿ P∨ ¿
¿ Q∨¿= √ 42+72
√ (−2¿¿ 2¿)+1+32 ¿ ¿ ¿
¿
∅ =cos−1 ¿
e. From trigonometry, we obtain equations 1, 5 and 8
sin(A-B)=sinAcosB-SinBsinA…….1
sin(x- π)=sinxcosπ-sinπcosx …..2
but cosπ=-1, sinπ=0…………3
hence sin(x-π)=-sinx……….4
Sin(A+B)=sinAcosB+sinBcosA…..5
Sin(x+π)=sinxcosπ+sinπcosx…….6
=-sinx+(0 ×cosx)=sinx……….7
Cos(A+B)=cosAcosB-sinAsinB……8
Cos(x+π/2)=cosxcosπ/2-sinxsiπ/2…..9
But cos(π/2)=0 and sin(π/2)=1……10
Hence cos(x+π/2)=(cosx×0)-sinx= -sinx…..11
Hence
Sin(x+π)=cos(x+π/2)=sin(x-π)= -sinx…..12
f. From equation 7 and equation 12, it is evident that,
1 Sin(x+π)=sin(x-π)= -sinx
2 Cos(x+π/2)=-sinx=sin(-x)
From equation 2, it is evident that the cosine of an angle ∅ 1 to be equal to the
cosine of angle ∅ 2 then the sum of the two angles has to be 90o
For example , x+ π/2+(-x)= π/2=90
Analytically
Letting x= π/2
Sin(π/2+ π)=sin(π/2- π)=-1
Cos(π/2+ π/2)=-sin(π/2)=sin(-π/2)=-1
Let x= π/4
Sin(π/4+ π)=sin(π/4- π)=-sin(π/4)=-1/ √2

Cos(π/4+ π/2)=-sin(π/4)=sin(-π/4)=-1/ √2
This confirms the trigonometric identities provided in the problem statement.
g. Sin(a+b)=sinacosb+sinbcosa
Sina=3/5, b=5/13
3/5cos(5/13)+sin(5/13)cos(arcsin(3/5))
=0.8563
LO4: Examine how differential and integral calculus can be used to solve engineering
problems
a. For a parallel connections of resistors,
1
R = 1
R 1 + 1
R 2 … … … … … ….. 1
Rewriting equation 1 to make R the subject,
R= R 1 R 2
R 1+R 2 … … … … … … … 2
dR
dt = d
dt ( R1 R 2
R 1+ R 2 )… … … … … … 3
Assigning the variables as shown below,
Letting R1R2 be x and R1+R2 be y,
x’=R1’(R2) +R’2(R1) =R’1(R2)
y’=R’1 +R’2 but from the problem statement, R’2 =0
Now, applying the quotient rule
d
dt ( x
y )= x' y− y ' x
y2
Substituting the actual differential variables,
dR
dt =
R 1 R 2 dR 1
dt + R 22+ R 1 R 2 dR 1
dt
(R 1+ R 2)2
b. From the problem statement,

V(t)=1+4t+3t2
Distance travelled within the 3rd minute is the integral of velocity between 2nd and 3rd minute
S=∫
2
3
v ( x ) dt
S=∫
2
3
1+ 4 t+ 3t2 dt
S=30 units
c.
1. Stress=F/A where A=πr2
40
π (0.0005)2 =50.93 ×106 N m−2
2. Y=stress/strain
2.1 ×106 =50.93 ×106
strain
strain=2.43 × 10−4
3. Strain= ∆ L
L
2.43 ×10−4= ∆ L
3
∆ L=7.28× 10−4
d. From the circuit theory and problem statement
1. V L ¿
I L=10 A
2. At t= ∞, s is opened
iL(∞)=0
V L ( ∞ )=∞
3. dV L/dt =5/4=1.25A/s
e. y=x3−6 x2 +9 x
From Calculus at a stationary point
dy
dx =0
dy
dx ( x3 −6 x2 +9 x )

dy
dx =3 x2 −12 x +9=0
Dividing all through by 3
x2−4 x+3=0
Factorizing the polynomial to solve for x
Product=3,
Sum=-4
The two numbers are -1 and -3
(x-1)(x-3)
X=1 or 3.
f. Substituting in y=x3−6 x2 +9 x
The coordinates of the stationary points are (-3,-108), and (-1, -16)
From calculus, a stationary point is maximum if the second derivative is negative and
minimum if second derivative is positive. From 1st derivative, second derivative,
dy2
d2 x =6 x+ 12
Subtitling the stationary x values,
At (-3,-108),
dy2
d2 x =−6
(Negative hence maxima point)
At (-1, -16)
dy2
d2 x =6
Negative hence minima

References
Bender, C. M., & Orszag, S. A. (2013). Advanced Mathematical Methods for Scientists and
Engineers I: Asymptotic Methods and Perturbation Theory. Berlin, Germany: Springer
Science & Business Media.
Bird, J. (2010). Higher Engineering Mathematics. London, England: Routledge.
Manoukian, E. B. (2012). Modern Concepts and Theorems of Mathematical Statistics. Berlin,
Germany: Springer Science & Business Media.
Navidi, W. C. (2010). Principles of Statistics for Engineers and Scientists. College Ie Overruns.
Occhiogrosso, M. (2010). Sequences and Series: Precalculus. Milliken Publishing Company.
O'Neil, P. V. (2011). Advanced Engineering Mathematics. Boston, MA: Cengage Learning.
Tang, K. (2016). Mathematical Methods for Engineers and Scientists 1: Complex Analysis,
Determinants and Matrices. Berlin, Germany: Springer Science & Business Media.
Zill, D., Wright, W. S., & Cullen, M. R. (2011). Advanced Engineering Mathematics.
Burlington, MA: Jones & Bartlett Learning.