Forecasting Humidity in London: A Data Analysis Report for LSC
VerifiedAdded on 2023/07/17
|19
|2116
|134
Report
AI Summary
This report presents a data analysis and forecasting exercise focused on humidity levels in London. The study involves collecting daily humidity measurements over ten days and organizing the data in Microsoft Excel. The analysis includes visual representation of the data using column and line charts, calculation of statistical measures such as mean, median, mode, range, and standard deviation, and the application of a linear forecasting model. The report details the formulas used in Excel, provides interpretations of the slope and intercept in the forecasting model, and presents the final results, offering a comprehensive overview of humidity trends in London during the specified period. This document is available on Desklib, a platform offering a wide range of study resources for students.
London School of Commerce In association with the University of
Suffolk
Assignment Brief
Course/Programme: BABS Foundation
Level: 3
Module Title: Numeracy and Data Analysis
Assignment title: Data Analysis and Forecasting
Submission date: 12th May 2023
Student Name: Alexandra Claudia Sterian
Student ID: S254561
Word Count: 1000 words
Suffolk
Assignment Brief
Course/Programme: BABS Foundation
Level: 3
Module Title: Numeracy and Data Analysis
Assignment title: Data Analysis and Forecasting
Submission date: 12th May 2023
Student Name: Alexandra Claudia Sterian
Student ID: S254561
Word Count: 1000 words
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1
Abstract
London, the capital of the United Kingdom, is widely regarded as a highly cosmopolitan
metropolis on a global scale. The location provides a plethora of contemporary art, trendy
cultural experiences, significant landmarks, unique trivia, essential cuisine, and verdant public
spaces. London offers a variety of attractions that make it a desirable destination. (Svet, 2021)
The present study is focused on determining the percentage values of humidity across four
contained in four parts of London.
The current research study involved the collection of daily humidity measurements spanning
from May 11th, 2023, to May 20th, 2023. Subsequently, the data was arranged using Microsoft
Excel, and the corresponding spreadsheet can be found in the Annexes chapter provided below.
Abstract
London, the capital of the United Kingdom, is widely regarded as a highly cosmopolitan
metropolis on a global scale. The location provides a plethora of contemporary art, trendy
cultural experiences, significant landmarks, unique trivia, essential cuisine, and verdant public
spaces. London offers a variety of attractions that make it a desirable destination. (Svet, 2021)
The present study is focused on determining the percentage values of humidity across four
contained in four parts of London.
The current research study involved the collection of daily humidity measurements spanning
from May 11th, 2023, to May 20th, 2023. Subsequently, the data was arranged using Microsoft
Excel, and the corresponding spreadsheet can be found in the Annexes chapter provided below.

2
Contents
Abstract ...................................................................................................................................... 1
Introduction ................................................................................................................................ 3
Task description ......................................................................................................................... 4
Task 1 ..................................................................................................................................... 4
Task 2 ..................................................................................................................................... 5
Column Chart ..................................................................................................................... 5
Line Chart ........................................................................................................................... 6
Task 3 ..................................................................................................................................... 7
I. Mean ............................................................................................................................ 7
II. Median ..................................................................................................................... 8
III. Mode ........................................................................................................................ 9
IV. Range ..................................................................................................................... 10
V. Standard Deviation .................................................................................................... 11
Task 4 ................................................................................................................................... 12
The meaning of the slope (m) and the intercept (c) .......................................................... 16
Conclusion ............................................................................................................................... 17
References ................................................................................................................................ 18
Annexes.................................................................................................................................... 18
Contents
Abstract ...................................................................................................................................... 1
Introduction ................................................................................................................................ 3
Task description ......................................................................................................................... 4
Task 1 ..................................................................................................................................... 4
Task 2 ..................................................................................................................................... 5
Column Chart ..................................................................................................................... 5
Line Chart ........................................................................................................................... 6
Task 3 ..................................................................................................................................... 7
I. Mean ............................................................................................................................ 7
II. Median ..................................................................................................................... 8
III. Mode ........................................................................................................................ 9
IV. Range ..................................................................................................................... 10
V. Standard Deviation .................................................................................................... 11
Task 4 ................................................................................................................................... 12
The meaning of the slope (m) and the intercept (c) .......................................................... 16
Conclusion ............................................................................................................................... 17
References ................................................................................................................................ 18
Annexes.................................................................................................................................... 18
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3
Introduction
The present study is organised into four distinct sections, which will be elaborated upon in the
subsequent discussion:
For the initial segment of this task, I opted to gather humidity data from London over a period
of ten consecutive days, from May 11th, 2023, to May 20th, 2023. Subsequently, I organised
the collected data in an Excel table, which is presented in the task description. For the duration
of this assignment, I have elected to gather data on humidity levels expressed as a percentage.
This collection will be ongoing until the completion of the task.
For the second phase of the project, I opted to visually depict the table data gathered on
humidity and wind speed in London through the use of two distinct types of diagrams, namely
the column diagram and the line diagram.
The third section of the document delineates the procedures for computing the mean, median,
mode, range, and standard deviation metrics in Excel. Additionally, the outcomes of these
computations are illustrated.
In the last section, the linear forecasting model was used to perform calculations in Excel. The
results were presented using formulas.
To summarise, I have included the Excel work as well as the programme I utilised for
evaluation in the Appendices section.
Introduction
The present study is organised into four distinct sections, which will be elaborated upon in the
subsequent discussion:
For the initial segment of this task, I opted to gather humidity data from London over a period
of ten consecutive days, from May 11th, 2023, to May 20th, 2023. Subsequently, I organised
the collected data in an Excel table, which is presented in the task description. For the duration
of this assignment, I have elected to gather data on humidity levels expressed as a percentage.
This collection will be ongoing until the completion of the task.
For the second phase of the project, I opted to visually depict the table data gathered on
humidity and wind speed in London through the use of two distinct types of diagrams, namely
the column diagram and the line diagram.
The third section of the document delineates the procedures for computing the mean, median,
mode, range, and standard deviation metrics in Excel. Additionally, the outcomes of these
computations are illustrated.
In the last section, the linear forecasting model was used to perform calculations in Excel. The
results were presented using formulas.
To summarise, I have included the Excel work as well as the programme I utilised for
evaluation in the Appendices section.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
4
Task description
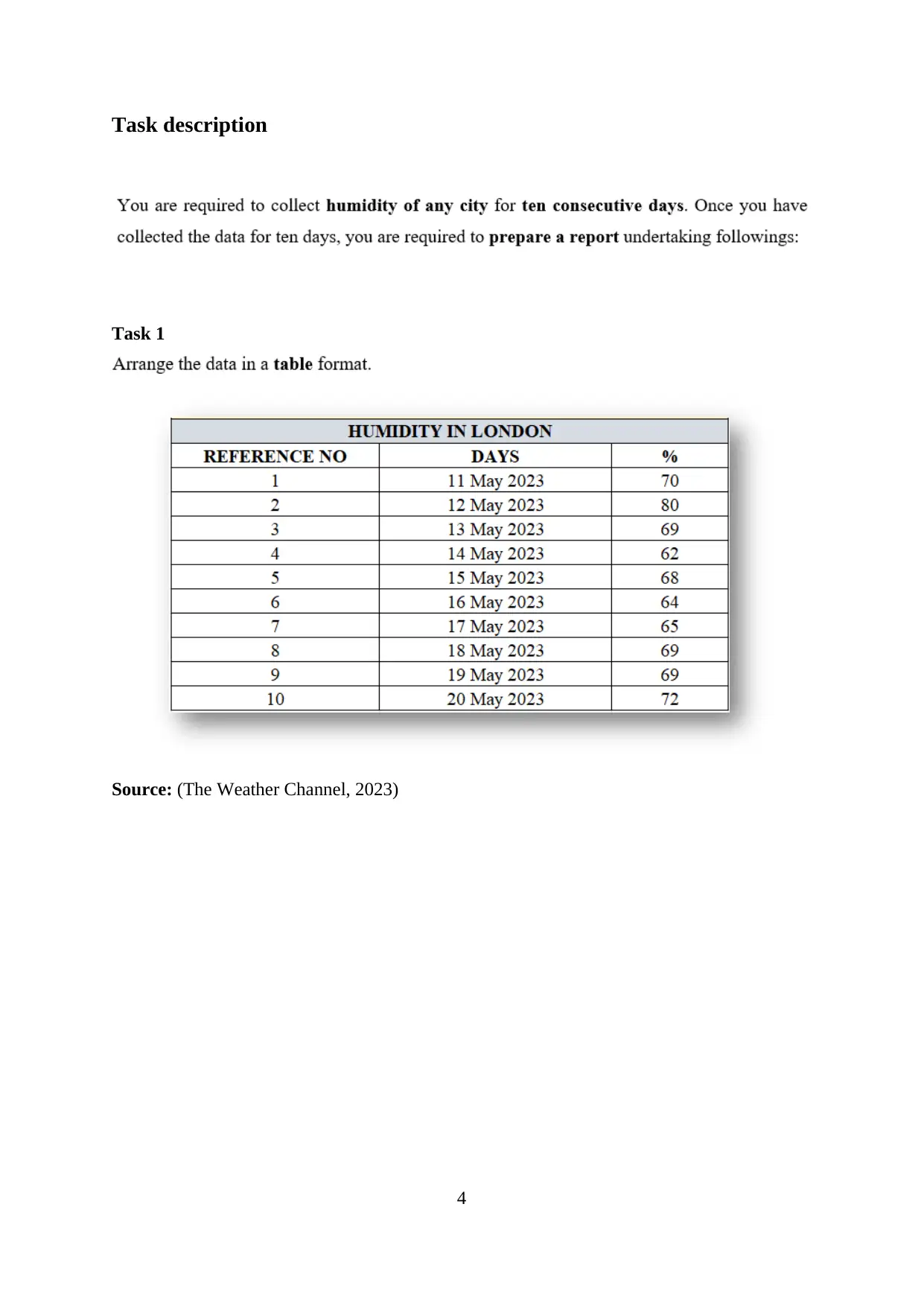
Task 1
Source: (The Weather Channel, 2023)
Task description
Task 1
Source: (The Weather Channel, 2023)
5
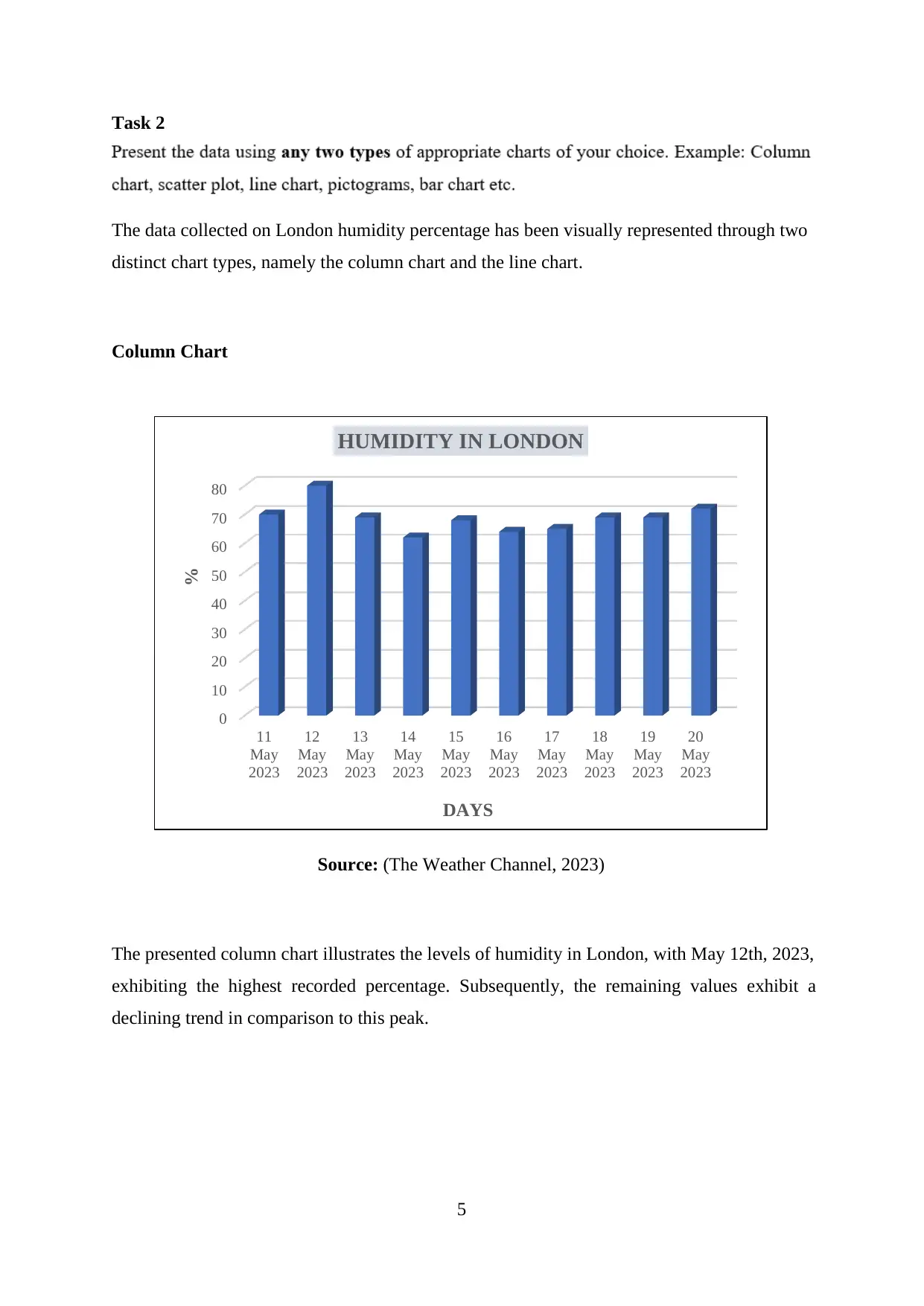
Task 2
The data collected on London humidity percentage has been visually represented through two
distinct chart types, namely the column chart and the line chart.
Column Chart
Source: (The Weather Channel, 2023)
The presented column chart illustrates the levels of humidity in London, with May 12th, 2023,
exhibiting the highest recorded percentage. Subsequently, the remaining values exhibit a
declining trend in comparison to this peak.
0
10
20
30
40
50
60
70
80
11
May
2023
12
May
2023
13
May
2023
14
May
2023
15
May
2023
16
May
2023
17
May
2023
18
May
2023
19
May
2023
20
May
2023
%
DAYS
HUMIDITY IN LONDON
Task 2
The data collected on London humidity percentage has been visually represented through two
distinct chart types, namely the column chart and the line chart.
Column Chart
Source: (The Weather Channel, 2023)
The presented column chart illustrates the levels of humidity in London, with May 12th, 2023,
exhibiting the highest recorded percentage. Subsequently, the remaining values exhibit a
declining trend in comparison to this peak.
0
10
20
30
40
50
60
70
80
11
May
2023
12
May
2023
13
May
2023
14
May
2023
15
May
2023
16
May
2023
17
May
2023
18
May
2023
19
May
2023
20
May
2023
%
DAYS
HUMIDITY IN LONDON
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6
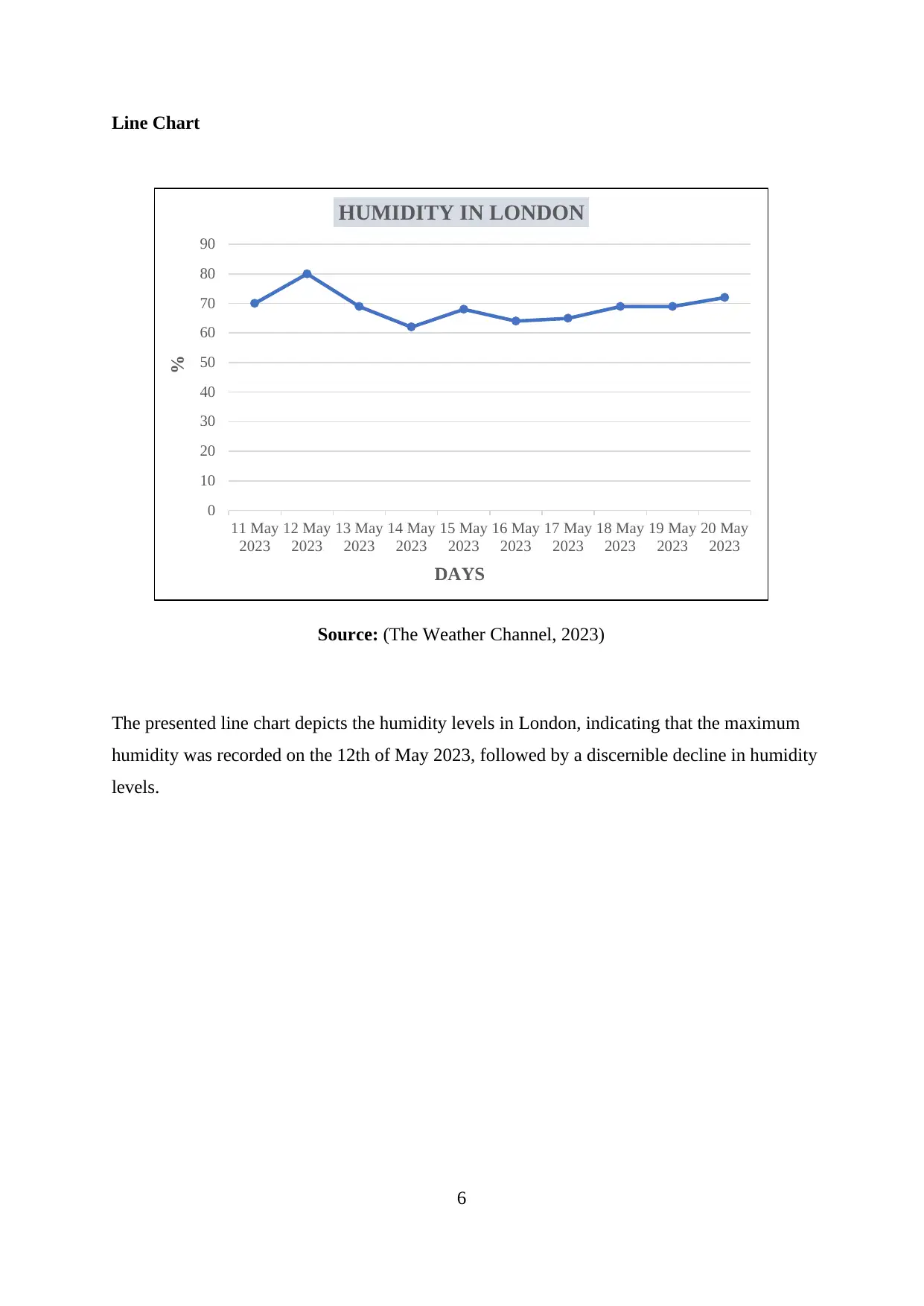
Line Chart
Source: (The Weather Channel, 2023)
The presented line chart depicts the humidity levels in London, indicating that the maximum
humidity was recorded on the 12th of May 2023, followed by a discernible decline in humidity
levels.
0
10
20
30
40
50
60
70
80
90
11 May
2023
12 May
2023
13 May
2023
14 May
2023
15 May
2023
16 May
2023
17 May
2023
18 May
2023
19 May
2023
20 May
2023
%
DAYS
HUMIDITY IN LONDON
Line Chart
Source: (The Weather Channel, 2023)
The presented line chart depicts the humidity levels in London, indicating that the maximum
humidity was recorded on the 12th of May 2023, followed by a discernible decline in humidity
levels.
0
10
20
30
40
50
60
70
80
90
11 May
2023
12 May
2023
13 May
2023
14 May
2023
15 May
2023
16 May
2023
17 May
2023
18 May
2023
19 May
2023
20 May
2023
%
DAYS
HUMIDITY IN LONDON
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7
Task 3
I. Mean
The arithmetic mean, commonly known as the average, is a measure that is likely to be the
most familiar to the reader. The arithmetic mean is determined through the summation of a set
of numerical values, followed by the division of the resulting sum by the total count of values
in the set. (Cheusheva, 2023)
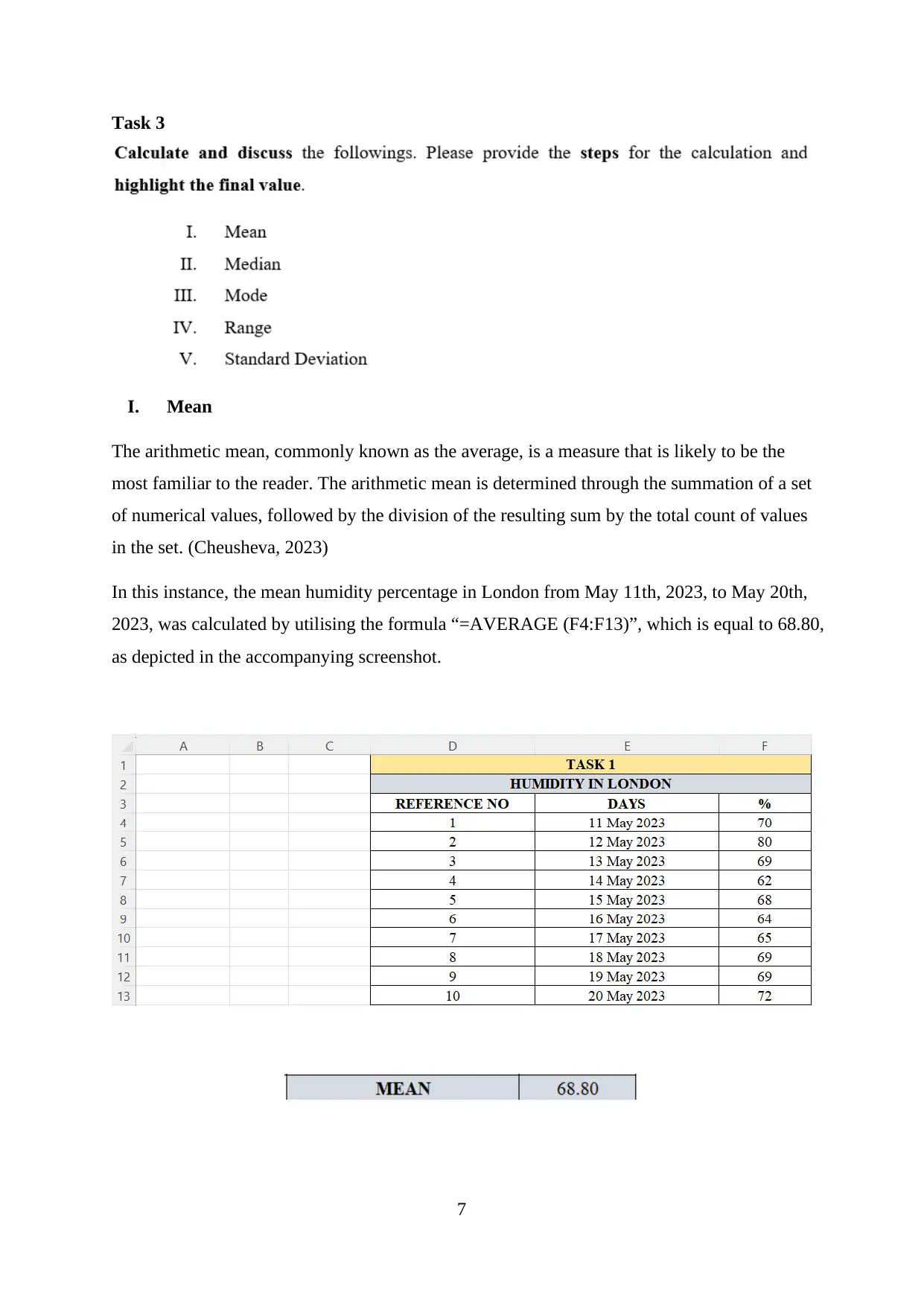
In this instance, the mean humidity percentage in London from May 11th, 2023, to May 20th,
2023, was calculated by utilising the formula “=AVERAGE (F4:F13)”, which is equal to 68.80,
as depicted in the accompanying screenshot.
Task 3
I. Mean
The arithmetic mean, commonly known as the average, is a measure that is likely to be the
most familiar to the reader. The arithmetic mean is determined through the summation of a set
of numerical values, followed by the division of the resulting sum by the total count of values
in the set. (Cheusheva, 2023)
In this instance, the mean humidity percentage in London from May 11th, 2023, to May 20th,
2023, was calculated by utilising the formula “=AVERAGE (F4:F13)”, which is equal to 68.80,
as depicted in the accompanying screenshot.
8
II. Median
The median is a statistical measure that represents the central value in a set of numbers that
have been arranged in either ascending or descending order. Specifically, it is the value that
divides the set into two equal halves, with half of the numbers being greater than the median
and the other half being less than the median. (Cheusheva, 2023)
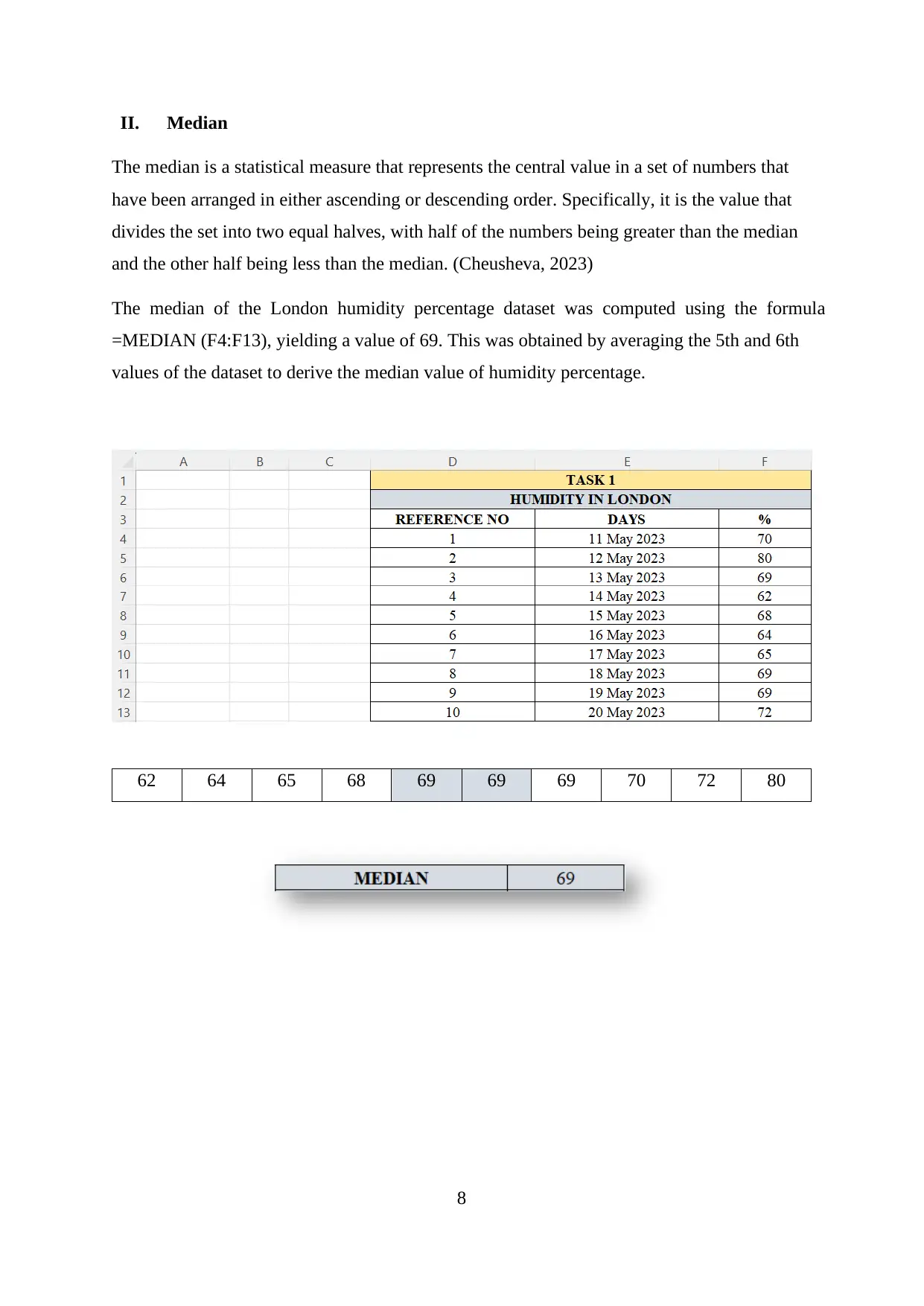
The median of the London humidity percentage dataset was computed using the formula
=MEDIAN (F4:F13), yielding a value of 69. This was obtained by averaging the 5th and 6th
values of the dataset to derive the median value of humidity percentage.
62 64 65 68 69 69 69 70 72 80
II. Median
The median is a statistical measure that represents the central value in a set of numbers that
have been arranged in either ascending or descending order. Specifically, it is the value that
divides the set into two equal halves, with half of the numbers being greater than the median
and the other half being less than the median. (Cheusheva, 2023)
The median of the London humidity percentage dataset was computed using the formula
=MEDIAN (F4:F13), yielding a value of 69. This was obtained by averaging the 5th and 6th
values of the dataset to derive the median value of humidity percentage.
62 64 65 68 69 69 69 70 72 80
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
9
III. Mode
The mode represents the value that appears most frequently in each dataset. The process of
determining the mode value involves a straightforward tallying of the frequency of each value,
in contrast to the mean and median, which necessitate mathematical computations. (Cheusheva,
2023)
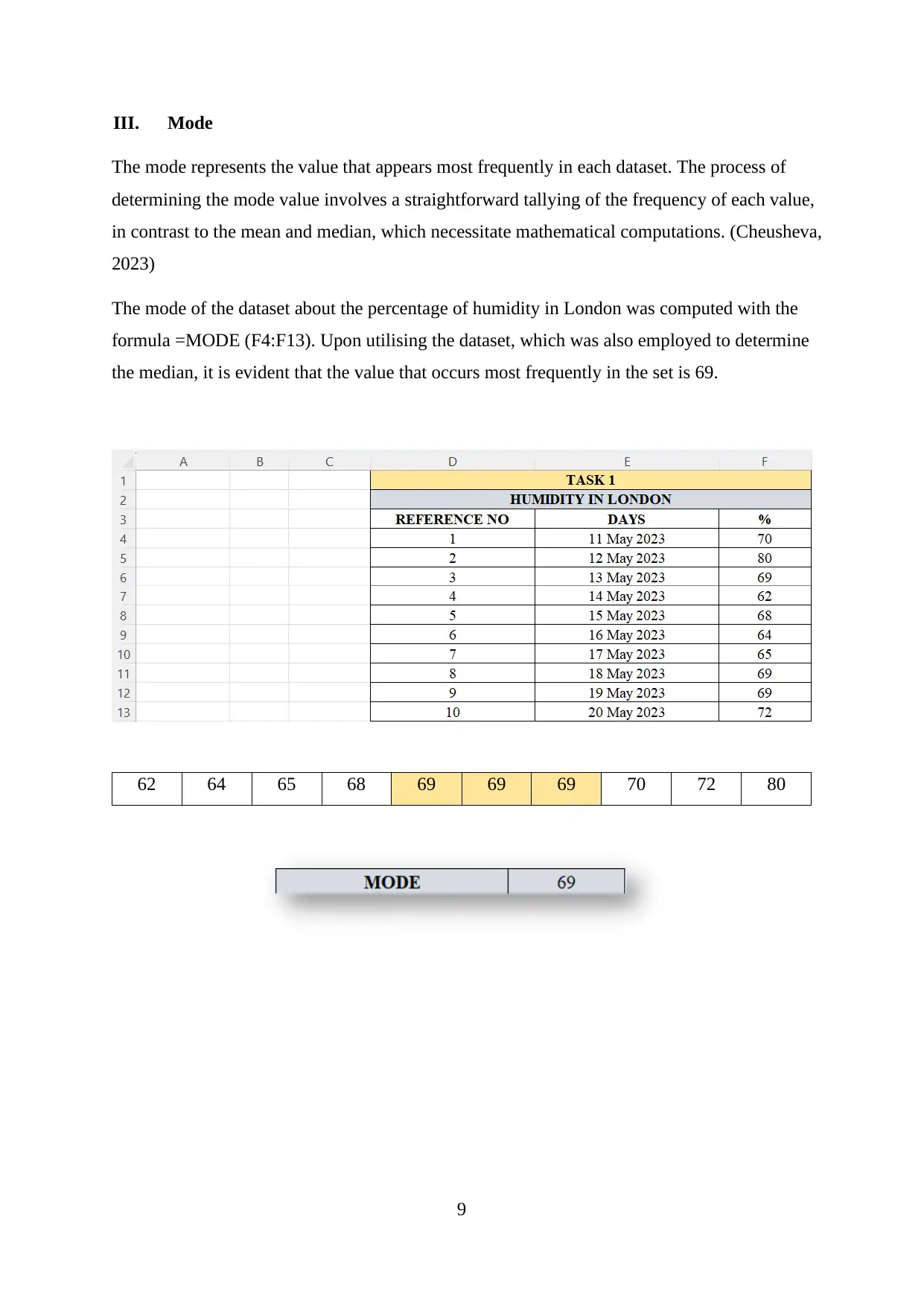
The mode of the dataset about the percentage of humidity in London was computed with the
formula =MODE (F4:F13). Upon utilising the dataset, which was also employed to determine
the median, it is evident that the value that occurs most frequently in the set is 69.
62 64 65 68 69 69 69 70 72 80
III. Mode
The mode represents the value that appears most frequently in each dataset. The process of
determining the mode value involves a straightforward tallying of the frequency of each value,
in contrast to the mean and median, which necessitate mathematical computations. (Cheusheva,
2023)
The mode of the dataset about the percentage of humidity in London was computed with the
formula =MODE (F4:F13). Upon utilising the dataset, which was also employed to determine
the median, it is evident that the value that occurs most frequently in the set is 69.
62 64 65 68 69 69 69 70 72 80
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
10
IV. Range
A range refers to a set of numerical values that are bounded by the highest and lowest values,
commonly known as the maximum and minimum values, respectively. In mathematical terms,
a range is defined as the disparity between the maximum and minimum values within a given
dataset. The term "range" refers to the extent or distribution of numerical values within a given
dataset. The calculation is performed using a straightforward formula. The range of a set of
data can be calculated by subtracting the minimum value from the maximum value. (Thakur,
2022)
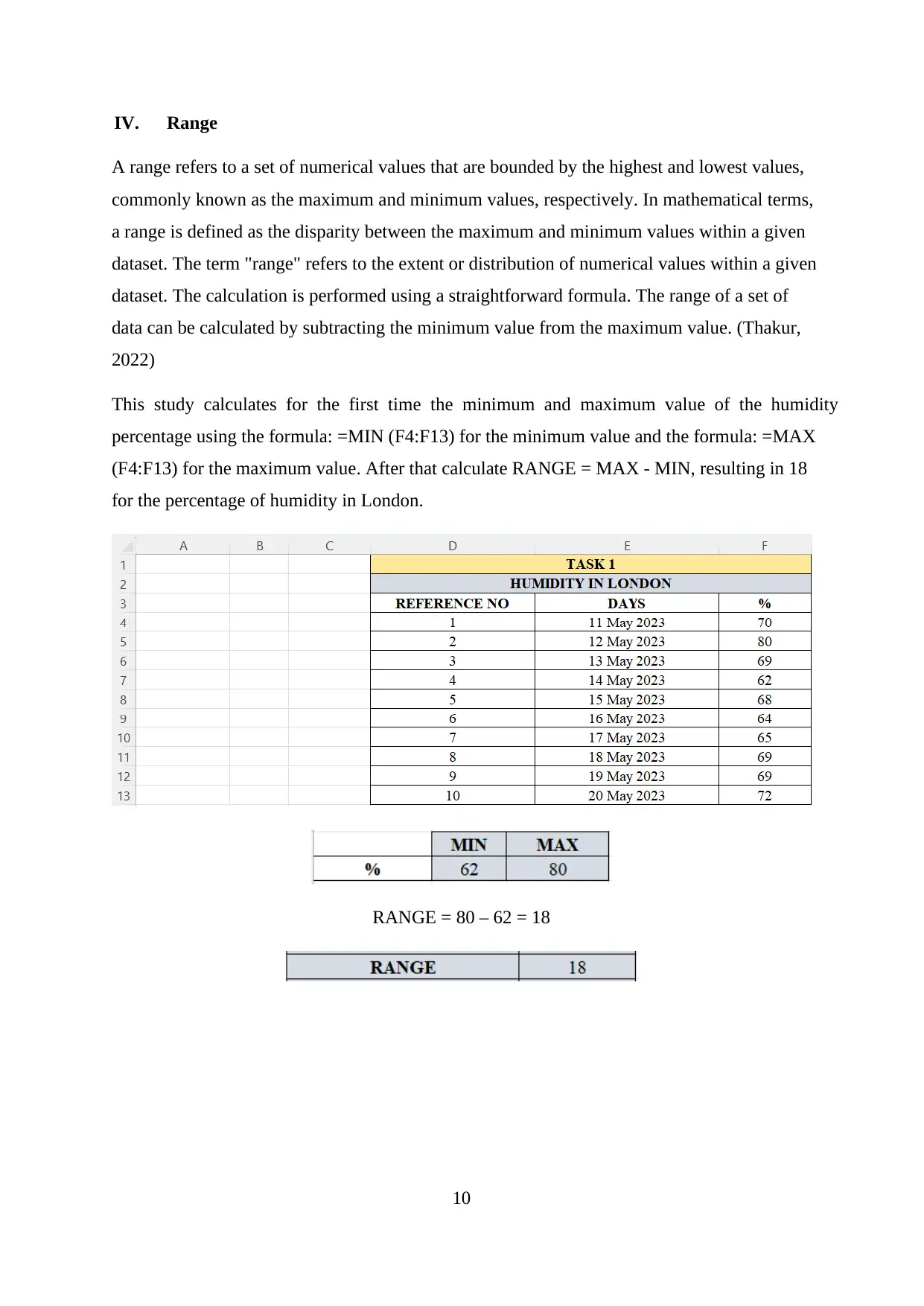
This study calculates for the first time the minimum and maximum value of the humidity
percentage using the formula: =MIN (F4:F13) for the minimum value and the formula: =MAX
(F4:F13) for the maximum value. After that calculate RANGE = MAX - MIN, resulting in 18
for the percentage of humidity in London.
RANGE = 80 – 62 = 18
IV. Range
A range refers to a set of numerical values that are bounded by the highest and lowest values,
commonly known as the maximum and minimum values, respectively. In mathematical terms,
a range is defined as the disparity between the maximum and minimum values within a given
dataset. The term "range" refers to the extent or distribution of numerical values within a given
dataset. The calculation is performed using a straightforward formula. The range of a set of
data can be calculated by subtracting the minimum value from the maximum value. (Thakur,
2022)
This study calculates for the first time the minimum and maximum value of the humidity
percentage using the formula: =MIN (F4:F13) for the minimum value and the formula: =MAX
(F4:F13) for the maximum value. After that calculate RANGE = MAX - MIN, resulting in 18
for the percentage of humidity in London.
RANGE = 80 – 62 = 18
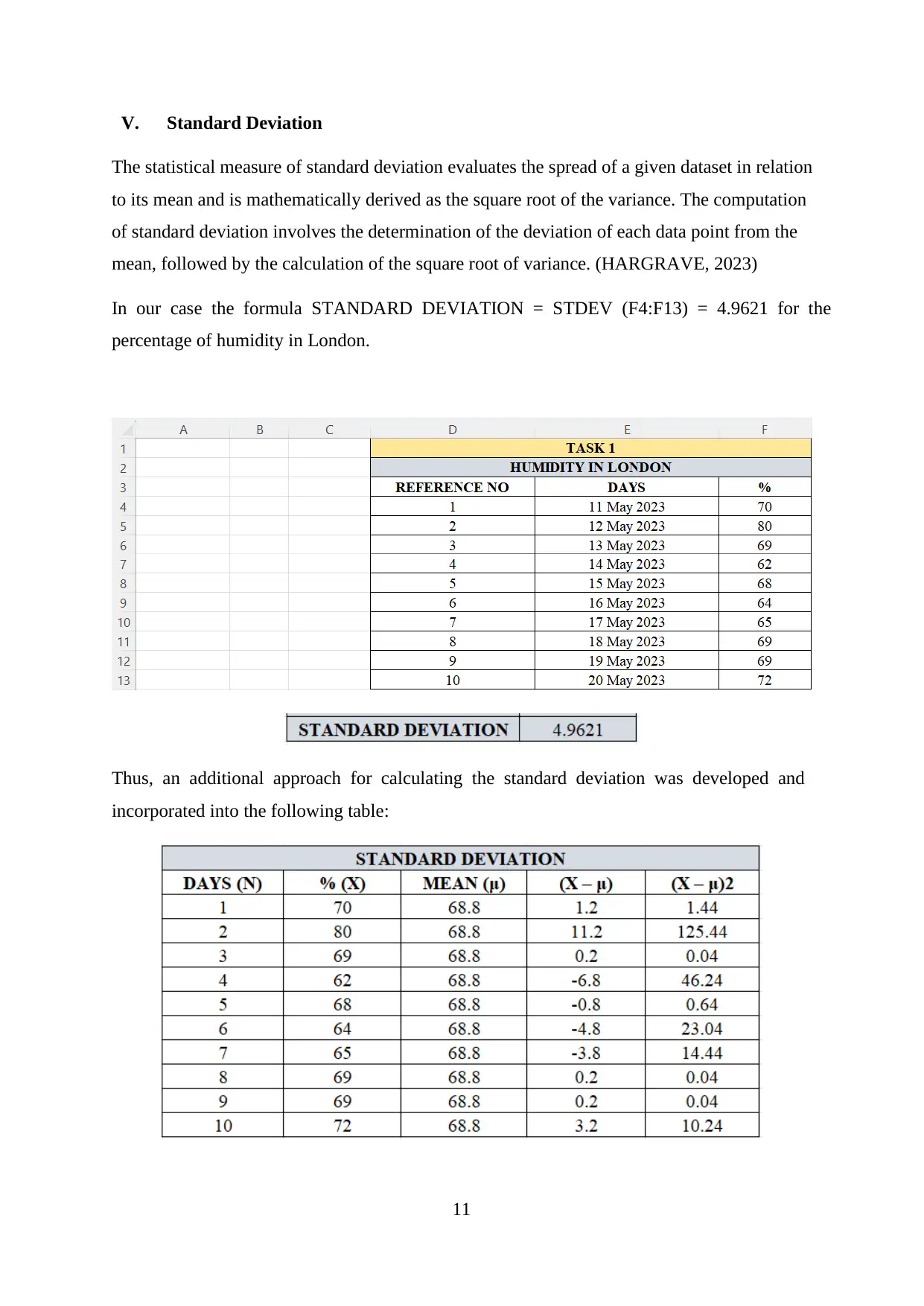
11
V. Standard Deviation
The statistical measure of standard deviation evaluates the spread of a given dataset in relation
to its mean and is mathematically derived as the square root of the variance. The computation
of standard deviation involves the determination of the deviation of each data point from the
mean, followed by the calculation of the square root of variance. (HARGRAVE, 2023)
In our case the formula STANDARD DEVIATION = STDEV (F4:F13) = 4.9621 for the
percentage of humidity in London.
Thus, an additional approach for calculating the standard deviation was developed and
incorporated into the following table:
V. Standard Deviation
The statistical measure of standard deviation evaluates the spread of a given dataset in relation
to its mean and is mathematically derived as the square root of the variance. The computation
of standard deviation involves the determination of the deviation of each data point from the
mean, followed by the calculation of the square root of variance. (HARGRAVE, 2023)
In our case the formula STANDARD DEVIATION = STDEV (F4:F13) = 4.9621 for the
percentage of humidity in London.
Thus, an additional approach for calculating the standard deviation was developed and
incorporated into the following table:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 19
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



