Comprehensive Solution: EMGT 5932 Logistics Management Homework 11

This document presents a detailed solution to a logistics management homework assignment focused on the Traveling Salesman Problem (TSP). The solution begins by constructing a tour graph and then applies the farthest insertion and nearest insertion heuristics to identify the optimal node t...Read More

Running head: MANAGEMENT LOGISTICS 1
Management Logistics
Name:
Institution affiliation:
Date:

MANAGEMENT LOGISTICS 2
Management Logistics
Question 1
We will start by drawing a tour graph showing all the costs between different towns.
a. Farthest insertion
In this part we will be inserting the node whose minimal travel cost to a tour results to
minimum.
We use the tour T = { 4−1−5−4 }
Starting our ˇwitth node 2
Next, we try with node 3
1
2 3
4
56
19
71
47
89
24
66
85
5784 49
68
83
65
53
57
2
3
4
1
5
4
1
53
19
65
47
85
57

MANAGEMENT LOGISTICS 3
Finally, we try with node 6
From the three diagrams we can conclude that:
Minimum cost of node 2 =19
Minimum travel cost of node 3 = 47
Minimum travel cost of node 6= 24
So, it is evident that has the maximum travel cost.
Therefore, the furthest insertion is Node 3.
b. Nearest insertion
Considering the TPS insertion schemes for the Nearest Insertion, we will chose a node among
the nodes which are inserted next to each other and we will give the minimum cost of the tour.
We will check the nodes apart from the nodes given in the current tour i.e. tour
T = { 4−1−5−4 } that gives the lowest increase in the cost of the tour.
The current node is T = { 4−1−5−4 }
The current cost of the tour cT ¿ 57+84 +89=230
Starting with node 2
We insert node 2 and check the cost of the tour
T = { 4−2−1−5−4 }
¿ 53+19+84 ++89
cT =245
Inserting Node 3
T = { 4−3−1−5−4 }
6
5
4
1
5
83
66
57

MANAGEMENT LOGISTICS 4
¿ 47 +85+84 +89
cT =305
Now inserting Node 6
T = { 4−6−1−5− 4 }
¿ 83+66 +84+89
cT =322
From the above, we find that Node 2 causes the least increase in the cost of the tours.
Therefore, the nearest insertion = Node 2
Question 2.
Given that the current tour is T = { 2−3− 4−2 } and node 1 to be inserted next in the current tour.
This will give us five possibilities
Now, Possibility 1
T = {1−2−3−4−2 }
Corresponding cost values are ¿ 19+71+47 +53
¿ 190
Possibility 2
T = {2−1−3−4−2 }
The corresponding cost values will be ¿ 19+85++ 47+53
¿ 204
Possibility 3
T = {2−3−1−4−2 }
The corresponding cost values will be ¿ 71+85+57+53
¿ 266
Possibility 4
T = {2−3− 4−1−2 }

MANAGEMENT LOGISTICS 5
The corresponding cost values will ¿ 71+47+57+19
¿ 194
Possibility 5
T = { 2−3− 4−2−1 }
The corresponding cost values will ¿ 71+47+53+19
¿ 190
We can see that 1st and 5th possibilities give minimum costs of insertion.
Question 3.
Given the current node to be T= {2-3-1-4-2}.
Taking node 1 and inserting in all the possibilities
1−2−3−1−4−2 :
19+71+85+57+ 53=285
2−1−3−1−4−2 :
19+85+85+57+53=299
2−3−1−1−4−2 :
71+85+0+57+53=266
2−3−1−4−1−2 :
71+85+57+ 57+19=289
2−3−1−4−2−1 :
71+85+57+ 53+ 19=285
Next, taking node 2 and inserting in all the possibilities
2−2−3−1−4−2

MANAGEMENT LOGISTICS 6
0+71+85+57+53=266
2−3−2−1−4−2
71+71+19+57+53=271
2−3−1−2−4−2
71+85+19+57+ 53=285
2−3−1−4−2−2
71+85+57+ 53+ 0=266
Next, we insert node 3 in all the possibilities
3−2−3−1−4−2
71+71+85+57++53=337
2−3−3−1−4−2
71+0+85+57++53=266
2−3−1−3−4−2
71+85+85+ 47+53=341
2−3−1−4−3−2
71+85+57+ 47+71=331
2−3−1−4−2−3
71+85+57+ 53+71=337
Finally, we insert node 4 in all the possibilities

MANAGEMENT LOGISTICS 7
4−2−3−1−4−2
53+71+85+57+ 53=319
2−4−3−1−4−2
53+47+85+57+ 53=295
2−3−4−1−4−2
71+47 +57+57+53=285
2−3−1−4−4−2
71+85+57+ 0+53=266
2−3−1−4−2−4
71+85+57+ 53+ 53=319
From the calculations we can now conclude that the minimum cost in the current tour is T = {2-
3-1-4-2} can only occur when a node is place adjacent to the same node.
Question 4.
Determine the cost of tour {2, 5, 6, 4, 3, 1, 2 }
Given that T =¿
¿ 65+24 +83+ 47+85+19
c { T }=323

MANAGEMENT LOGISTICS 8
Question 5
Beginning at the known city (nodes) 1 and 2 as directed by the question, we move to the next
near node 6, still following the rule as we move to neighboring node 5, then the next neighbor 3
and finally the next city is 4.
The graph showing the current path is below.
The next two iterations of the nearest neighbor
We will repeat the same procedure and reduce the number of nodes to a total of 4. Starting at any
edge from the current graph drawn above.
First iterations
1 2
3
4
5
6
18
57
47
57
24
49
c(P)=252
5
6
2
1
18
24
65
66
c(P)=173

MANAGEMENT LOGISTICS 9
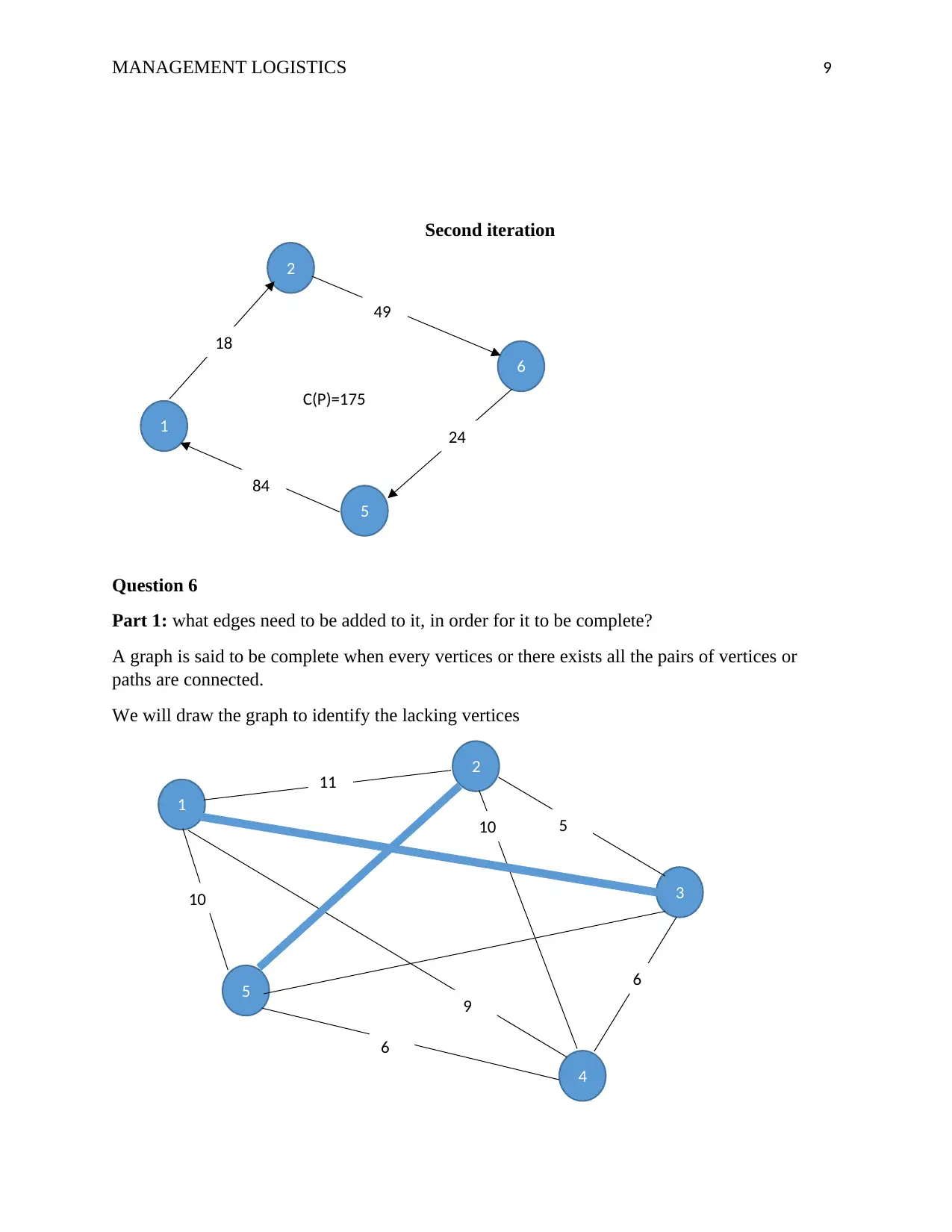
Second iteration
Question 6
Part 1: what edges need to be added to it, in order for it to be complete?
A graph is said to be complete when every vertices or there exists all the pairs of vertices or
paths are connected.
We will draw the graph to identify the lacking vertices
1
5
2
6
18
49
24
84
C(P)=175
1
2
3
4
5
10
6
5
11
6
9
10

MANAGEMENT LOGISTICS
10
From our graph, we can now see that the vertices (1, 3) and (2, 5) lack vertices.
Therefore, the graph to be complete, it needs to have edges connecting 1 and 3 vertices, and 2
and 5 vertices.
Part 2: what should the cost on those new edges be, in order for the edge costs to satisfy the
triangle-inequality?
Solution
The costs of the two lacking edges need to satisfy triangle inequality, which states for any
triangle, the total sum of the lengths of any two sides need to be equal to or greater than the
remaining side.
Now, our edge between 1and 3 ≤ 11+ 5
The edge between 2 and 5 ≤ 12
Question 7
Before the two exchange
1
2
3
4
5
10
11
10
6
7

MANAGEMENT LOGISTICS
11
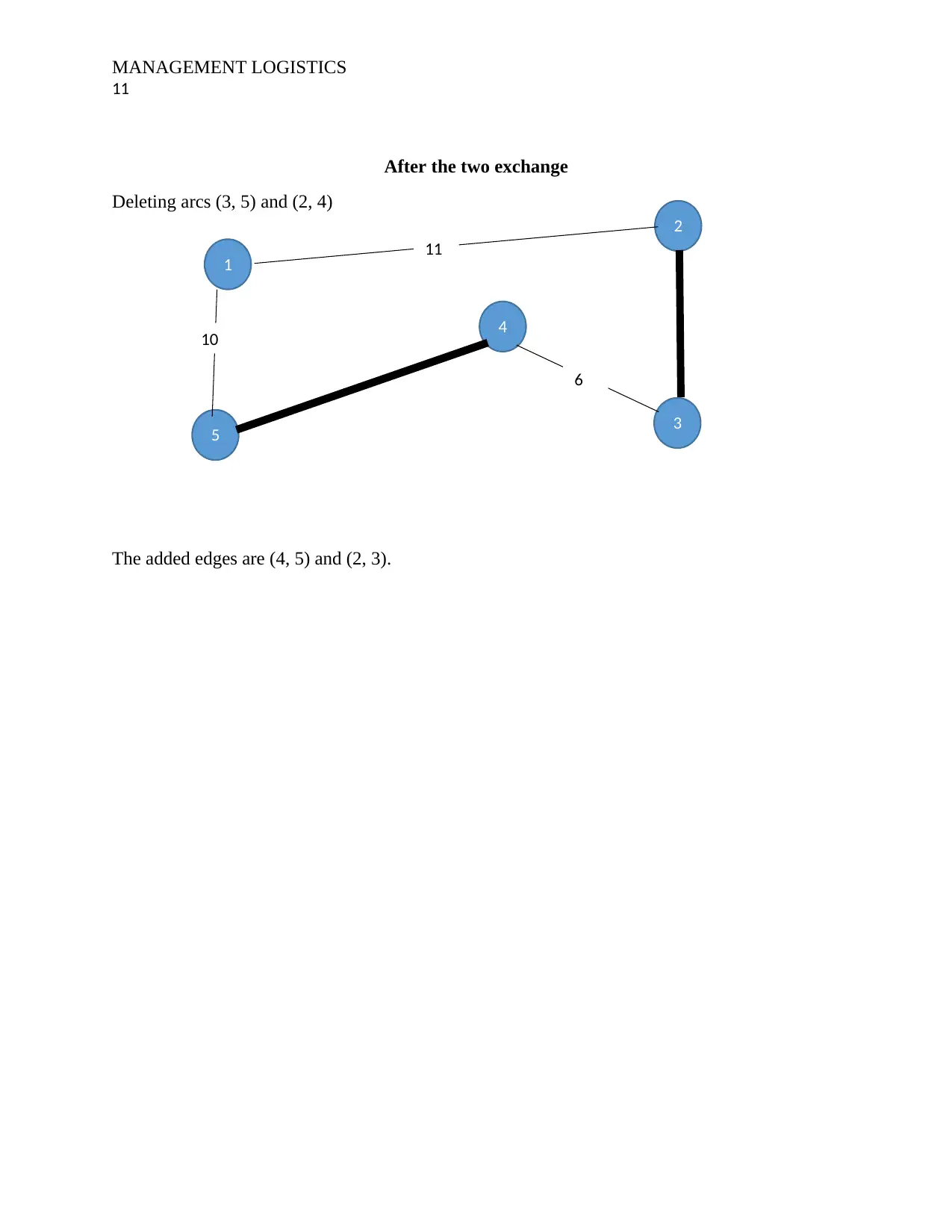
After the two exchange
Deleting arcs (3, 5) and (2, 4)
The added edges are (4, 5) and (2, 3).
5
4
3
1
2
11
10
6

MANAGEMENT LOGISTICS
12
References
Taillard, É. D., & Helsgaun, K. (2019). POPMUSIC for the travelling salesman
problem. European Journal of Operational Research, 272(2), 420-429.
Agatz, N., Bouman, P., & Schmidt, M. (2018). Optimization approaches for the traveling
salesman problem with drone. Transportation Science, 52(4), 965-981.
Lourenço, H. R., Martin, O. C., & Stützle, T. (2019). Iterated local search: Framework and
applications. In Handbook of metaheuristics (pp. 129-168). Springer,
Cham.
Cortinhal, M. J., Mourão, M. C., & Nunes, A. C. (2016). Local search heuristics for sectoring
routing in a household waste collection context. European Journal of
Operational Research, 255(1), 68-79.