Difference Between Dead Loads, Imposed Load Live Loads and Wind Loads

This article explains the difference between dead loads, imposed load live loads and wind loads in civil engineering. It covers the concepts of Gk, gk, Qk, qk, and the response of buildings to high wind pressures. The article also discusses the main differences between the ULS (Ultimate Limit State) and SLS (Serviceability Limit State) in structural design. Additionally, it provides design information for a steel building in Wellington, including the determination of regional wind speed, terrain/height multiplier, wind direction multiplier, shielding multiplier, and topographical multiplier.

MANUKAU INSTITUTE OF TECHNOLOGY
FACULTY OF ENGINEERING & TRADES
TewāhangawhakaakoPūkengaHangaPūkengaTauhokohoko
SCHOOL OF PROFESSIONAL ENGINEERING
Bachelor of Engineering Technology
Project
Civil Engineering
242.611 Structural Steel and Timber
Semester 1 - 2019
1- Briefly explain the difference between dead loads, imposed load live loads and wind
loads.
I. Dead Loads Gk, gk
Dead loads are all the permanent loads acting on the structure including self-weight,
finishes, fixtures and partitions. The symbols Gk and gk are usually used to denote
total and uniformly distributed characteristic dead loads respectively.
II. Imposed Load Qk qk
Imposed load are sometimes referred to as live load and they represent the load due
to the proposed occupancy including the weights of the occupants, furniture, and
roof loads including snow loads.
III. Wind Loads
The response of a building to high wind pressures depends not only upon the
geographical location and proximity of other obstructions to airflow but also upon
the characteristics of the structure itself. The effect of wind on the structure as a
whole is determined by the combined action of external and internal pressures
acting upon it.

2- What the main differences between the ULS (Ultimate Limit State) and SLS
(serviceability limit state)?
Ultimate Limit State Design is a limit state that can cause failure of the structure. This
type of limit states allow the designer to analyse the strength of the structure. On the other
hand, Serviceability limit state model the behaviour of the structure at working loads.
Moreover, there are several limit states which may unfavourably affect the performance of
the structure e.g. durability and fire resistance.
3- The ground floor and elevation of plans of a steel structure are shown in Figure 1, 2
and 3. This building is located in the Wellington area at a site about 850m above sea
level. The intended use is retail shop space on ground floor and office space on first
floor. The building design working life is 100 years.
Determine the following giving a short explanation in each case:
a) Regional wind speed (𝑉𝑅) for ULS design.
VR, the Regional wind speed, is well-defined as a 3-second gust wind speed. It
is a multi-directional basic action because no considerations on direction from
which wind gust is originated are made. Its unit of measure is metres/second. In
order to obtain this value, a return period R, defined as the reciprocal of the
annual probability of exceedance must be evaluated.
VR, REGION B=106 - 92.R-0.1
(𝑉100=48 Table 3.1 AS/NZS 1170.2:2002)
b) Terrain/height multiplier (𝑀𝑧,𝑎𝑡).
Terrain, over which the approach wind flows towards a structure, is assessed on
the basis of the below category accounts:
Category 1—Exposed open terrain with few or no obstructions and water
surfaces at serviceability wind speeds.
Category 2—Water surfaces, open terrain, grassland with few, well-scattered
obstructions having heights generally from 1.5 m to 10 m.

Category 3—Terrain with numerous closely spaced obstructions 3 m to 5 m
high such as areas of suburban housing.
Category 4—Terrain with numerous large, high (10 m to 30 m high) and closely
spaced obstructions such as large city centres and well-developed industrial
complexes.
𝑀𝑧,𝑐𝑎𝑡. Wellington= 1.03 since it lies in category 4 (Table 4.1by interpolation)
AS/NZS 1170.2:2002
c) Wind direction multiplier (𝑀𝑑) for the building orthogonal axis 𝜃 = 0°, given
that the axis points South-East.
The wind direction multiplier Md is the adjustment of the regional wind speed to
cater for directional characteristics of the regional wind hazard at the site under
consideration in eight cardinal directions. It determines the directional effect on
the magnitude of the wind speed.
The wind direction multiplier (Md) for all directions in region B = 0.95 for
determining the resultant forces and overturning moments on complete
buildings and wind actions on major structural elements.
Shielding multiplier (𝑀𝑠) if two similar buildings are located within a 45°sector of
radius 300m.
Shielding phenomenon is quantified by the shielding multiplier Ms used to adjust
the wind speed when shielding objects are within the upwind shielding zone of a
building. The shielding multiplier Ms in design practice leads to a reduction in
design loads.
Ls= h(10/ns +5)
=6(10/180 +5)
=30.05
ls = average spacing of shielding buildings
hs = average roof height of shielding buildings
bs = average breadth of shielding buildings, normal to the wind stream
h = average roof height, above ground, of the structure being shielded

ns = number of upwind shielding buildings within a 45° sector of radius 20h and
with hs ≥ z
s= ls/ (hs. bs)0.5
30.05/(10 x 10) 0.5
=3.05 From AS/NZS 1170.2:2002 table 4.3
𝑀𝑠=0.8
d) The topographical multiplier (𝑀𝑡) if the building is sited 500m upwind of a
250m high hill crest, and the hill has an average slope (
The topographic multiplier Mt estimates the accelerating effect of wind speeds
on an uphill slope downwind of a flat region caused by the shape and slope of
undulating terrain. Hilly terrains greatly influence the passing wind flow, with
both valleys and hill crests experiencing stronger wind speeds than over flat
terrain.
Mt = Mh=1.0
where Mh = hill shape multiplier
Mlee = lee (effect) multiplier (taken as 1.0)
e) The site wind speed (𝑉𝑠𝑖𝑡,) in terms of 𝑀𝑑.
(𝑉𝑠𝑖𝑡,𝛽)= 𝑉𝑅. 𝑀𝑧,𝑐𝑎𝑡.𝑀𝑑. 𝑀𝑠. 𝑀𝑡
=48 x 1.03 x 0.95 x 0.8 x 1.0
=37.5744 m/s
f) The design wind speed (𝑉𝑑𝑒𝑠,) for 𝜃 = 0°.
Since (𝑉𝑑𝑒𝑠,) for 𝜃 = 0°. Then 𝑉𝑠𝑖𝑡, = 𝑉𝑑𝑒𝑠,𝜃 = 37.57m/s
g) The building design wind pressure if the aerodynamic shape factor is 1.3.
4- The figures below (Figure 1, 2 and 3) show a ground and elevation plan of a two-
storied steel building to be construct in Wellington. Drawing is not to scale. All units
are in meter. This is a steel building with the beams along the grids A, B and C
supporting the reinforced concrete slab with thickness of 200mm. All columns are

rigidly connected to the concrete footings. Use appropriate analysis or computer
analysis to determine the loads on requested steel structure.
Design Information:
Use an additional superimposed dead load of 2 kPa acting on the floor.
Load effects should include Gravity and wind loads.
Steel grade 300
Density of concrete is 24𝑘𝑁⁄𝑚2.
All design and detailing should be in accordance with NZS3404 and loading should be
in accordance with NZS1170.
a) Design the steel beams B:1-2 and B:2-3, bracing C:2-3 along with column B2 for the
ground floor of the building.
b) Find the axial compression force on foundations under column B2 and B3.
Note: you need to consider wind and gravity load and should use the appropriate load
combination.
c) Design the connections for requested beams and braces (bolt connection or weld
connection)

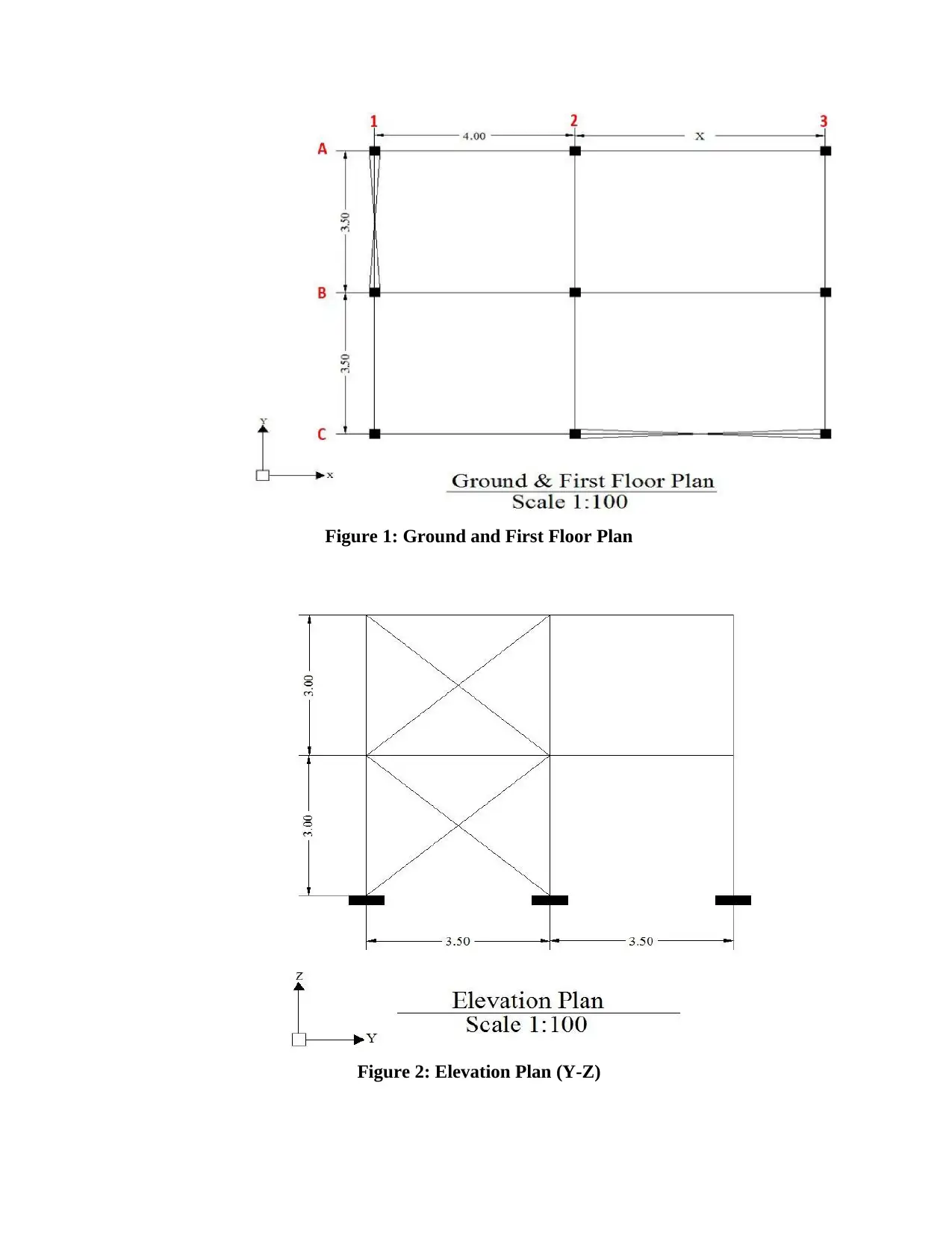
Figure 1: Ground and First Floor Plan
Figure 2: Elevation Plan (Y-Z)

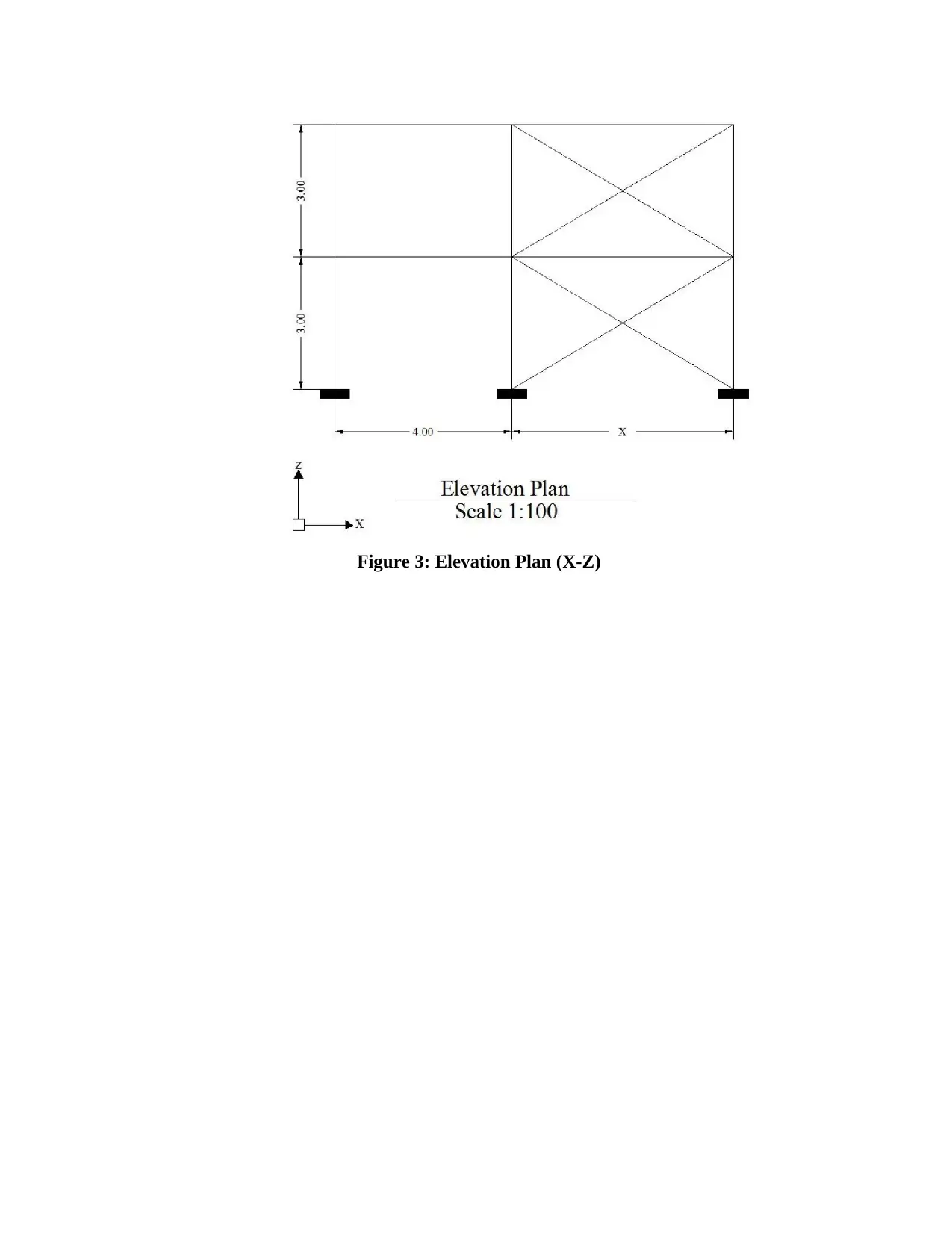
Figure 3: Elevation Plan (X-Z)