EGR2005M: Compressible Flow Analysis Through a Sonic Nozzle
VerifiedAdded on 2023/06/15
|11
|2641
|205
Practical Assignment
AI Summary
This assignment solution delves into the analysis of compressible fluid flow through a converging nozzle, focusing on determining the mass flow rate at choked conditions and the critical pressure ratio. It includes theoretical derivations, such as the application of Bernoulli's equation for adiabatic flow, and experimental procedures to assess the impact of inlet and back pressures on the airflow rate. The experiments involve adjusting pressure regulators, measuring temperatures and pressures, and comparing the experimental results with theoretical calculations. The document also provides a detailed explanation of sonic nozzle principles, applications, and operational characteristics, including the effects of compressibility and the advantages of using sonic nozzles for maintaining steady inlet flow. The results are presented in tables and graphs, illustrating the relationship between pressure and airflow rate, and are compared against theoretical values.

MASS FLOW RATE THROUGH CONVERGING NOZZLE
FLOW RATE EQUATION AT CHOCKED CONDITION OF COMPRESSIBLE FLUID
THROUGH A CONVERGENT NOZZLE & CRITICAL PRESSURE RATIO AT CHOCKED
CONDITION
Assuming the flow to take place adiabatically, then by using Bernoulli’s equation (for
adiabatic flow), we have
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=Ratio of specific heat 1.4 for air
R=Gasconstant of air
( γ
γ −1 ) p1
ρ1 g + V 1
2
2 g + z1=( γ
γ −1 ) p2
ρ2 g + V 2
2
2 g + z2
But z1 = z2 and V1 = 0
( γ
γ −1 ) p1
ρ1 g = ( γ
γ−1 ) p2
ρ2 g + V 2
2
2 g
( γ
γ −1 ) ( p1
ρ1 g − p2
ρ2 g )=V 2
2
2 g
( γ
γ −1 ) ( p1
ρ1
− p2
ρ2 )= V 2
2
2
V 2= √( 2 γ
γ −1 ) ( p1
ρ1
− p2
ρ2 )
V 2= √( 2 γ
γ −1 ) p1
ρ1 (1− p2
ρ2
− p1
ρ1 )…….1
For adiabatic flow
ρ1
ρ2
=
( p1
p2 ) 1
γ …….2
Put above value in 1
V 2= √( 2 γ
γ −1 ) p1
ρ1 ( 1−( p2
p1 ) γ−1
γ
)
The mass rate of flow of the compressible fluid,
m = 2A2V2, A2 being the area of the nozzle at the exit
1 | P a g e
FLOW RATE EQUATION AT CHOCKED CONDITION OF COMPRESSIBLE FLUID
THROUGH A CONVERGENT NOZZLE & CRITICAL PRESSURE RATIO AT CHOCKED
CONDITION
Assuming the flow to take place adiabatically, then by using Bernoulli’s equation (for
adiabatic flow), we have
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=Ratio of specific heat 1.4 for air
R=Gasconstant of air
( γ
γ −1 ) p1
ρ1 g + V 1
2
2 g + z1=( γ
γ −1 ) p2
ρ2 g + V 2
2
2 g + z2
But z1 = z2 and V1 = 0
( γ
γ −1 ) p1
ρ1 g = ( γ
γ−1 ) p2
ρ2 g + V 2
2
2 g
( γ
γ −1 ) ( p1
ρ1 g − p2
ρ2 g )=V 2
2
2 g
( γ
γ −1 ) ( p1
ρ1
− p2
ρ2 )= V 2
2
2
V 2= √( 2 γ
γ −1 ) ( p1
ρ1
− p2
ρ2 )
V 2= √( 2 γ
γ −1 ) p1
ρ1 (1− p2
ρ2
− p1
ρ1 )…….1
For adiabatic flow
ρ1
ρ2
=
( p1
p2 ) 1
γ …….2
Put above value in 1
V 2= √( 2 γ
γ −1 ) p1
ρ1 ( 1−( p2
p1 ) γ−1
γ
)
The mass rate of flow of the compressible fluid,
m = 2A2V2, A2 being the area of the nozzle at the exit
1 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MASS FLOW RATE THROUGH CONVERGING NOZZLE
m=ρ 2 A 2 √( 2 γ
γ −1 ) p1
ρ1 ( 1−
( p2
p1 ) γ−1
γ
)
m= A 2 √ ( 2 γ
γ −1 ) p1
ρ1
ρ22
(1−( p2
p1 )γ −1
γ
)……3
From equation 2
ρ1
ρ2
=( p1
p2 )1
γ
ρ2
2=ρ1
2
( p2
p1 )2
γ
Put above value in Eqn 3 we get
m= A 2 √ ( 2 γ
γ −1 ) p1 ρ1 ( ( p2
p1 )2
γ −
( p2
p1 )γ +1
γ
)
The mass rate of flow (m) depends on the value of p2
p1
Value of p2
p1
for maximum mass flow rate:
For maximum value of m we have
d ( m )
d ( p2
p1 ) =0
Put the value of m from above
As critical pressure value
( ( p2
p1 )=( 2
γ +1 ) γ
γ−1
)
Maximum value of flow rate m at critical pressure
mmax=A 2 √( 2 γ
γ −1 ) p1 ρ 1 (( p2
p1 ) 2
γ − ( p2
p1 ) γ +1
γ
)
mmax=A 2 √( 2 γ
γ −1 ) p1 ρ 1 (( 2
γ +1 ) 2
γ −1 − ( 2
γ +1 )γ + 1
γ−1
)
Put γ=1.4for air
mmax =A 2 √7 p1 ρ1 ( 0.4018−0.3348 )
2 | P a g e
m=ρ 2 A 2 √( 2 γ
γ −1 ) p1
ρ1 ( 1−
( p2
p1 ) γ−1
γ
)
m= A 2 √ ( 2 γ
γ −1 ) p1
ρ1
ρ22
(1−( p2
p1 )γ −1
γ
)……3
From equation 2
ρ1
ρ2
=( p1
p2 )1
γ
ρ2
2=ρ1
2
( p2
p1 )2
γ
Put above value in Eqn 3 we get
m= A 2 √ ( 2 γ
γ −1 ) p1 ρ1 ( ( p2
p1 )2
γ −
( p2
p1 )γ +1
γ
)
The mass rate of flow (m) depends on the value of p2
p1
Value of p2
p1
for maximum mass flow rate:
For maximum value of m we have
d ( m )
d ( p2
p1 ) =0
Put the value of m from above
As critical pressure value
( ( p2
p1 )=( 2
γ +1 ) γ
γ−1
)
Maximum value of flow rate m at critical pressure
mmax=A 2 √( 2 γ
γ −1 ) p1 ρ 1 (( p2
p1 ) 2
γ − ( p2
p1 ) γ +1
γ
)
mmax=A 2 √( 2 γ
γ −1 ) p1 ρ 1 (( 2
γ +1 ) 2
γ −1 − ( 2
γ +1 )γ + 1
γ−1
)
Put γ=1.4for air
mmax =A 2 √7 p1 ρ1 ( 0.4018−0.3348 )
2 | P a g e

MASS FLOW RATE THROUGH CONVERGING NOZZLE
mmax=0.685 A 2 √ p1 ρ1
Theoretical mass flow rate at chocked condition :-
mmax=0.685 A 2 √ p1 ρ1
INTRODUCTION
A nozzle is a device in which the kinetic energy of a fluid is increased in an
adiabatic process. This increase involves a decrease in pressure and is
accomplished by the proper change in flow area. A diffuser is a device that has the
opposite function, namely, to increase the pressure by decelerating the fluid.
Its principle is based on the fact that the gas flow accelerates to the critical
velocity at the nozzle throat (this being equal to the local sonic velocity). At the
critical velocity, the mass flow-rate of the gas flowing through the Venturi nozzle
is the maximum possible for the existing upstream conditions.
In these conditions, the mass flow rate through a sonic nozzle is
determined from the stagnation pressure and temperature
measurements and the calculation of the thermodynamic
coefficients.
Compressibility becomes important for High Speed Flows where M > 0.3
M < 0.3 - Subsonic & incompressible
0.3 < M < 0.8 - Subsonic & compressible
0.8 < M < 1.2 - Transonic: shock waves appear mixed subsonic and sonic flow
regime
1.2 < M < 3.0 - Supersonic: shock waves are present but NO subsonic flow
M > 3.0 - Hypersonic: shock waves and other flow changes are very strong
Significant changes in velocity and pressure result in density variations throughout a
flow field
Large Temperature variations result in density variations
Compressible flow is shown by:-
∂ ρ
∂t ≠ 0
Principal
The simplest flow system would use an inlet pressure regulator to control air
3 | P a g e
mmax=0.685 A 2 √ p1 ρ1
Theoretical mass flow rate at chocked condition :-
mmax=0.685 A 2 √ p1 ρ1
INTRODUCTION
A nozzle is a device in which the kinetic energy of a fluid is increased in an
adiabatic process. This increase involves a decrease in pressure and is
accomplished by the proper change in flow area. A diffuser is a device that has the
opposite function, namely, to increase the pressure by decelerating the fluid.
Its principle is based on the fact that the gas flow accelerates to the critical
velocity at the nozzle throat (this being equal to the local sonic velocity). At the
critical velocity, the mass flow-rate of the gas flowing through the Venturi nozzle
is the maximum possible for the existing upstream conditions.
In these conditions, the mass flow rate through a sonic nozzle is
determined from the stagnation pressure and temperature
measurements and the calculation of the thermodynamic
coefficients.
Compressibility becomes important for High Speed Flows where M > 0.3
M < 0.3 - Subsonic & incompressible
0.3 < M < 0.8 - Subsonic & compressible
0.8 < M < 1.2 - Transonic: shock waves appear mixed subsonic and sonic flow
regime
1.2 < M < 3.0 - Supersonic: shock waves are present but NO subsonic flow
M > 3.0 - Hypersonic: shock waves and other flow changes are very strong
Significant changes in velocity and pressure result in density variations throughout a
flow field
Large Temperature variations result in density variations
Compressible flow is shown by:-
∂ ρ
∂t ≠ 0
Principal
The simplest flow system would use an inlet pressure regulator to control air
3 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

MASS FLOW RATE THROUGH CONVERGING NOZZLE
pressure and a thermocouple to measure temperature. Adjusting the pressure
regulator will change and maintain the flow through the Nozzle.
Pressure differences within a piping system travel at the speed of sound and
generate flow. Downstream pressure disturbances cannot move upstream past
the throat of the Nozzle because the throat velocity is higher and in the opposite
direction. Since these pressure disturbances cannot move upstream past the
throat, they cannot affect the velocity or the density of the flow through the
Nozzle. This is what is referred to as a choked or sonic state of operation. This is
one of the greatest advantages of Sonic Nozzles when compared to subsonic
flow-meters (Venturis or Orifice Plates where any change in downstream
pressure will affect the differential pressure across the flow-meter, which in
turn, affects the flow).
As a result, Sonic Nozzles are ideal for applications where steady inlet flow is
required even though there is pulsating or varying gas consumption
downstream. They are also ideal as flow limiters since with a fixed upstream
pressure both mass and volumetric flows are fixed.
Accuracy levels of ±0.25% of reading or better can routinely be achieved since
there are no moving parts.
APPLICATIONS
• Applications where the assumptions of steady, uniform, isentropic flow are
reasonable:
• Exhaust gasses passing through the blades of a turbine.
• Diffuser near the front of a jet engine
• Nozzles on a rocket engine
• A broken natural gas line
Solution-2
Experiment -1
Aim :- To determine the effect of inlet pressure on the air flow rate (m) and
compare it with theoretical calculations.
Procedure:-
1. Close the air inlet throttle valve 3.
2. Adjust the inlet pressure to approx 700-900 kPa (gauge) using pressure
regulator and open the throttle valve. Open the back pressure valve and
then close it slightly to get a back pressure of 20-50kPa
3. Observe the inlet ,outlet temperature ,pressure and flow rates.
4 | P a g e
pressure and a thermocouple to measure temperature. Adjusting the pressure
regulator will change and maintain the flow through the Nozzle.
Pressure differences within a piping system travel at the speed of sound and
generate flow. Downstream pressure disturbances cannot move upstream past
the throat of the Nozzle because the throat velocity is higher and in the opposite
direction. Since these pressure disturbances cannot move upstream past the
throat, they cannot affect the velocity or the density of the flow through the
Nozzle. This is what is referred to as a choked or sonic state of operation. This is
one of the greatest advantages of Sonic Nozzles when compared to subsonic
flow-meters (Venturis or Orifice Plates where any change in downstream
pressure will affect the differential pressure across the flow-meter, which in
turn, affects the flow).
As a result, Sonic Nozzles are ideal for applications where steady inlet flow is
required even though there is pulsating or varying gas consumption
downstream. They are also ideal as flow limiters since with a fixed upstream
pressure both mass and volumetric flows are fixed.
Accuracy levels of ±0.25% of reading or better can routinely be achieved since
there are no moving parts.
APPLICATIONS
• Applications where the assumptions of steady, uniform, isentropic flow are
reasonable:
• Exhaust gasses passing through the blades of a turbine.
• Diffuser near the front of a jet engine
• Nozzles on a rocket engine
• A broken natural gas line
Solution-2
Experiment -1
Aim :- To determine the effect of inlet pressure on the air flow rate (m) and
compare it with theoretical calculations.
Procedure:-
1. Close the air inlet throttle valve 3.
2. Adjust the inlet pressure to approx 700-900 kPa (gauge) using pressure
regulator and open the throttle valve. Open the back pressure valve and
then close it slightly to get a back pressure of 20-50kPa
3. Observe the inlet ,outlet temperature ,pressure and flow rates.
4 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
MASS FLOW RATE THROUGH CONVERGING NOZZLE
4. Reduce the inlet pressure by regulator then again adjust the back
pressure to 20-50Kpa
5. Repeat this process until inlet pressure equal to outlet pressure.
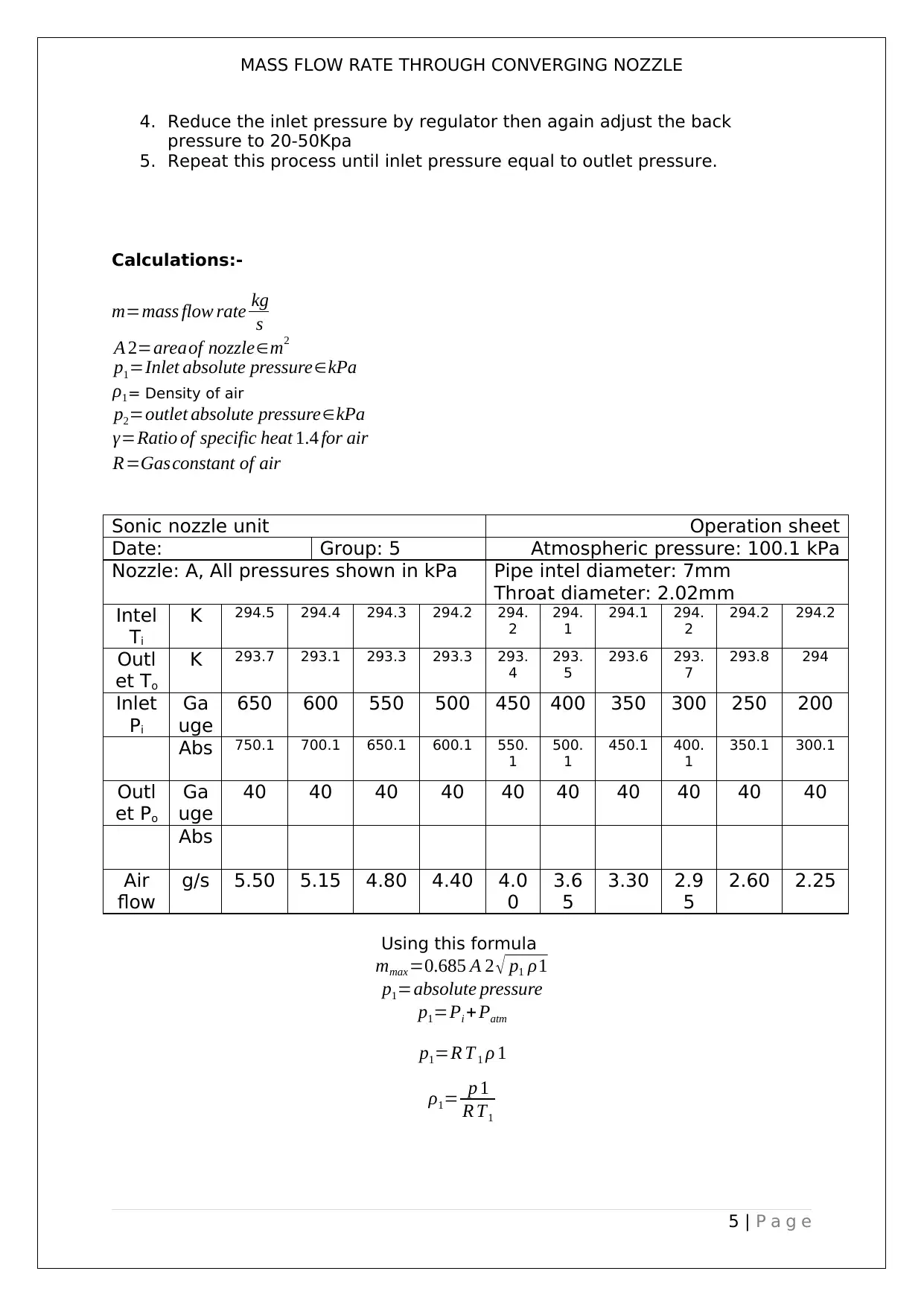
Calculations:-
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=Ratio of specific heat 1.4 for air
R=Gasconstant of air
Sonic nozzle unit Operation sheet
Date: Group: 5 Atmospheric pressure: 100.1 kPa
Nozzle: A, All pressures shown in kPa Pipe intel diameter: 7mm
Throat diameter: 2.02mm
Intel
Ti
K 294.5 294.4 294.3 294.2 294.
2
294.
1
294.1 294.
2
294.2 294.2
Outl
et To
K 293.7 293.1 293.3 293.3 293.
4
293.
5
293.6 293.
7
293.8 294
Inlet
Pi
Ga
uge
650 600 550 500 450 400 350 300 250 200
Abs 750.1 700.1 650.1 600.1 550.
1
500.
1
450.1 400.
1
350.1 300.1
Outl
et Po
Ga
uge
40 40 40 40 40 40 40 40 40 40
Abs
Air
flow
g/s 5.50 5.15 4.80 4.40 4.0
0
3.6
5
3.30 2.9
5
2.60 2.25
Using this formula
mmax=0.685 A 2 √ p1 ρ1
p1=absolute pressure
p1=Pi + Patm
p1=R T 1 ρ 1
ρ1= p 1
R T1
5 | P a g e
4. Reduce the inlet pressure by regulator then again adjust the back
pressure to 20-50Kpa
5. Repeat this process until inlet pressure equal to outlet pressure.
Calculations:-
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=Ratio of specific heat 1.4 for air
R=Gasconstant of air
Sonic nozzle unit Operation sheet
Date: Group: 5 Atmospheric pressure: 100.1 kPa
Nozzle: A, All pressures shown in kPa Pipe intel diameter: 7mm
Throat diameter: 2.02mm
Intel
Ti
K 294.5 294.4 294.3 294.2 294.
2
294.
1
294.1 294.
2
294.2 294.2
Outl
et To
K 293.7 293.1 293.3 293.3 293.
4
293.
5
293.6 293.
7
293.8 294
Inlet
Pi
Ga
uge
650 600 550 500 450 400 350 300 250 200
Abs 750.1 700.1 650.1 600.1 550.
1
500.
1
450.1 400.
1
350.1 300.1
Outl
et Po
Ga
uge
40 40 40 40 40 40 40 40 40 40
Abs
Air
flow
g/s 5.50 5.15 4.80 4.40 4.0
0
3.6
5
3.30 2.9
5
2.60 2.25
Using this formula
mmax=0.685 A 2 √ p1 ρ1
p1=absolute pressure
p1=Pi + Patm
p1=R T 1 ρ 1
ρ1= p 1
R T1
5 | P a g e
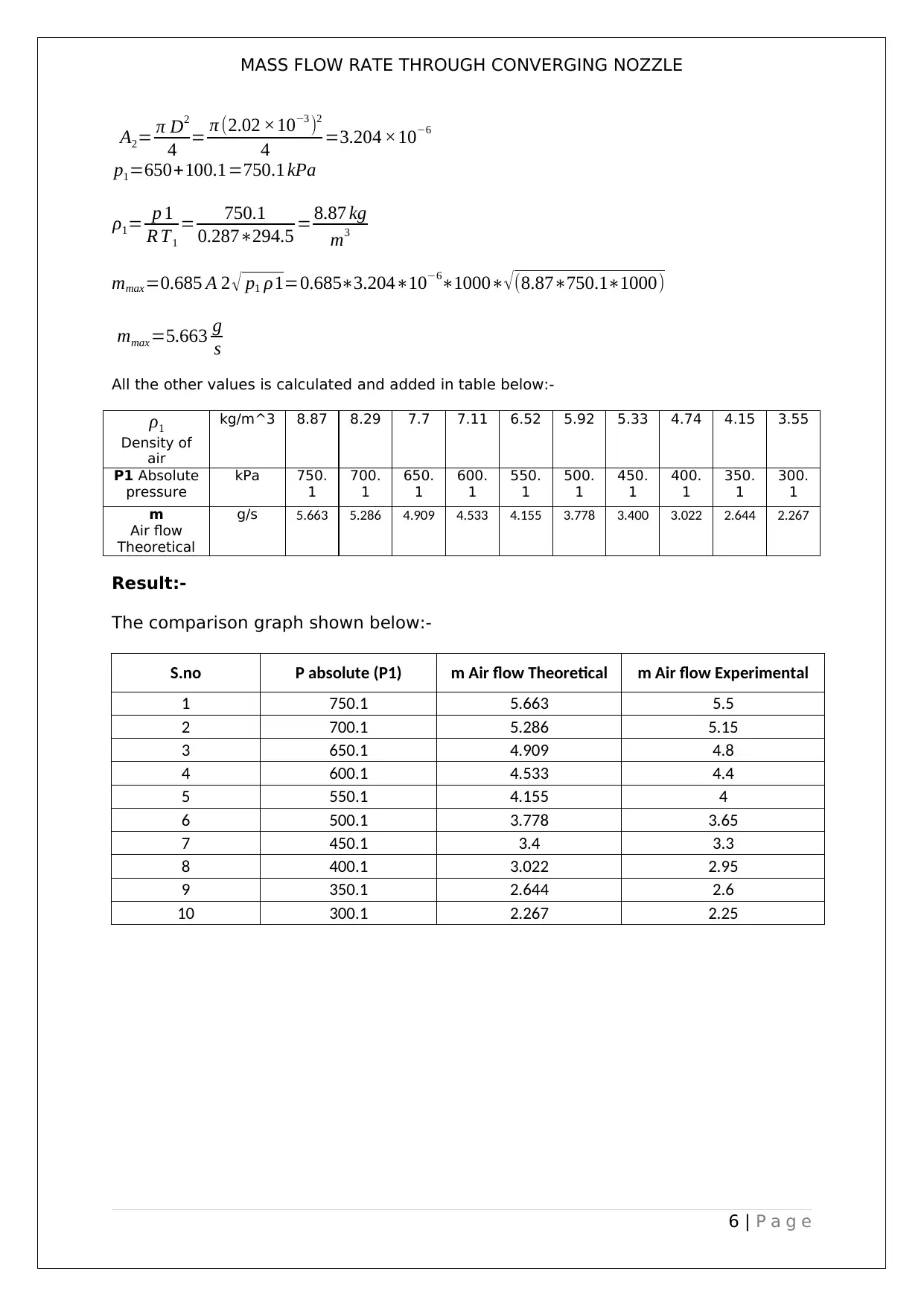
MASS FLOW RATE THROUGH CONVERGING NOZZLE
A2= π D2
4 = π (2.02 ×10−3 )2
4 =3.204 ×10−6
p1=650+100.1=750.1 kPa
ρ1= p 1
R T1
= 750.1
0.287∗294.5 = 8.87 kg
m3
mmax=0.685 A 2 √ p1 ρ1=0.685∗3.204∗10−6∗1000∗√(8.87∗750.1∗1000)
mmax =5.663 g
s
All the other values is calculated and added in table below:-
ρ1
Density of
air
kg/m^3 8.87 8.29 7.7 7.11 6.52 5.92 5.33 4.74 4.15 3.55
P1 Absolute
pressure
kPa 750.
1
700.
1
650.
1
600.
1
550.
1
500.
1
450.
1
400.
1
350.
1
300.
1
m
Air flow
Theoretical
g/s 5.663 5.286 4.909 4.533 4.155 3.778 3.400 3.022 2.644 2.267
Result:-
The comparison graph shown below:-
S.no P absolute (P1) m Air flow Theoretical m Air flow Experimental
1 750.1 5.663 5.5
2 700.1 5.286 5.15
3 650.1 4.909 4.8
4 600.1 4.533 4.4
5 550.1 4.155 4
6 500.1 3.778 3.65
7 450.1 3.4 3.3
8 400.1 3.022 2.95
9 350.1 2.644 2.6
10 300.1 2.267 2.25
6 | P a g e
A2= π D2
4 = π (2.02 ×10−3 )2
4 =3.204 ×10−6
p1=650+100.1=750.1 kPa
ρ1= p 1
R T1
= 750.1
0.287∗294.5 = 8.87 kg
m3
mmax=0.685 A 2 √ p1 ρ1=0.685∗3.204∗10−6∗1000∗√(8.87∗750.1∗1000)
mmax =5.663 g
s
All the other values is calculated and added in table below:-
ρ1
Density of
air
kg/m^3 8.87 8.29 7.7 7.11 6.52 5.92 5.33 4.74 4.15 3.55
P1 Absolute
pressure
kPa 750.
1
700.
1
650.
1
600.
1
550.
1
500.
1
450.
1
400.
1
350.
1
300.
1
m
Air flow
Theoretical
g/s 5.663 5.286 4.909 4.533 4.155 3.778 3.400 3.022 2.644 2.267
Result:-
The comparison graph shown below:-
S.no P absolute (P1) m Air flow Theoretical m Air flow Experimental
1 750.1 5.663 5.5
2 700.1 5.286 5.15
3 650.1 4.909 4.8
4 600.1 4.533 4.4
5 550.1 4.155 4
6 500.1 3.778 3.65
7 450.1 3.4 3.3
8 400.1 3.022 2.95
9 350.1 2.644 2.6
10 300.1 2.267 2.25
6 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
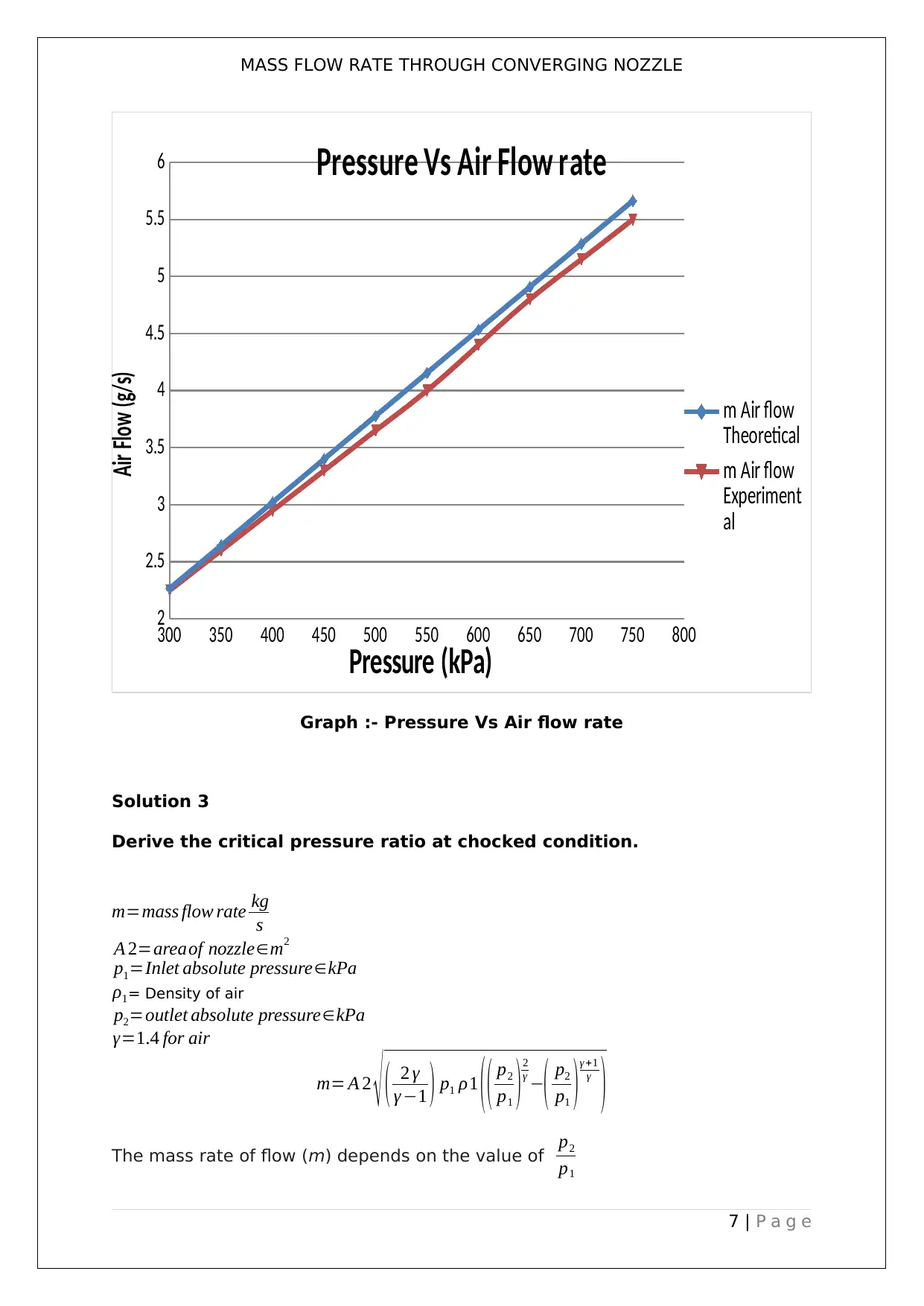
MASS FLOW RATE THROUGH CONVERGING NOZZLE
300 350 400 450 500 550 600 650 700 750 800
2
2.5
3
3.5
4
4.5
5
5.5
6 Pressure Vs Air Flow rate
m Air flow
Theoretical
m Air flow
Experiment
al
Pressure (kPa)
Air Flow (g/s)
Graph :- Pressure Vs Air flow rate
Solution 3
Derive the critical pressure ratio at chocked condition.
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=1.4 for air
m= A 2 √ ( 2 γ
γ −1 ) p1 ρ1 ( ( p2
p1 )2
γ −( p2
p1 )γ +1
γ
)
The mass rate of flow (m) depends on the value of p2
p1
7 | P a g e
300 350 400 450 500 550 600 650 700 750 800
2
2.5
3
3.5
4
4.5
5
5.5
6 Pressure Vs Air Flow rate
m Air flow
Theoretical
m Air flow
Experiment
al
Pressure (kPa)
Air Flow (g/s)
Graph :- Pressure Vs Air flow rate
Solution 3
Derive the critical pressure ratio at chocked condition.
m=mass flow rate kg
s
A 2=areaof nozzle∈m2
p1=Inlet absolute pressure∈kPa
ρ1= Density of air
p2=outlet absolute pressure∈kPa
γ=1.4 for air
m= A 2 √ ( 2 γ
γ −1 ) p1 ρ1 ( ( p2
p1 )2
γ −( p2
p1 )γ +1
γ
)
The mass rate of flow (m) depends on the value of p2
p1
7 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MASS FLOW RATE THROUGH CONVERGING NOZZLE
Value of p2
p1
for maximum mass flow rate:
For maximum value of m we have
d ( m )
d ( p2
p1 ) =0
Put the value of m from above
d (( ( p2
p1 )2
γ −
( p2
p1 )γ +1
γ
) )
d ( p2
p1 ) =0
( 2
γ ( p2
p1 )2
γ −1
− γ +1
γ ( p2
p1 )γ+ 1
γ −1
)=0
( ( p2
p1 )2
γ −1
= γ+1
2 ( p2
p1 )1
γ
)=0
( ( p2
p1 )
2−γ
=( γ +1
2 )
γ
( p2
p1 ))
( ( p2
p1 )γ −1
= ( 2
γ +1 )γ
)
( ( p2
p1 )=( 2
γ +1 ) γ
γ−1
)
γ=1.4 for air
( p2
p1 )= ( 2
1.4 +1 ) 1.4
1.4 −1
p2
p1
=0.528
Solution 4
Experiment -2
Aim :- To determine the effect of back pressure on the air flow rate (m) and
compare it with theoretical calculations at chocked condition.
Procedure:-
1. Close the air inlet throttle valve 3.
2. Adjust the inlet pressure to approx 700-900 kPa (gauge) using pressure
8 | P a g e
Value of p2
p1
for maximum mass flow rate:
For maximum value of m we have
d ( m )
d ( p2
p1 ) =0
Put the value of m from above
d (( ( p2
p1 )2
γ −
( p2
p1 )γ +1
γ
) )
d ( p2
p1 ) =0
( 2
γ ( p2
p1 )2
γ −1
− γ +1
γ ( p2
p1 )γ+ 1
γ −1
)=0
( ( p2
p1 )2
γ −1
= γ+1
2 ( p2
p1 )1
γ
)=0
( ( p2
p1 )
2−γ
=( γ +1
2 )
γ
( p2
p1 ))
( ( p2
p1 )γ −1
= ( 2
γ +1 )γ
)
( ( p2
p1 )=( 2
γ +1 ) γ
γ−1
)
γ=1.4 for air
( p2
p1 )= ( 2
1.4 +1 ) 1.4
1.4 −1
p2
p1
=0.528
Solution 4
Experiment -2
Aim :- To determine the effect of back pressure on the air flow rate (m) and
compare it with theoretical calculations at chocked condition.
Procedure:-
1. Close the air inlet throttle valve 3.
2. Adjust the inlet pressure to approx 700-900 kPa (gauge) using pressure
8 | P a g e
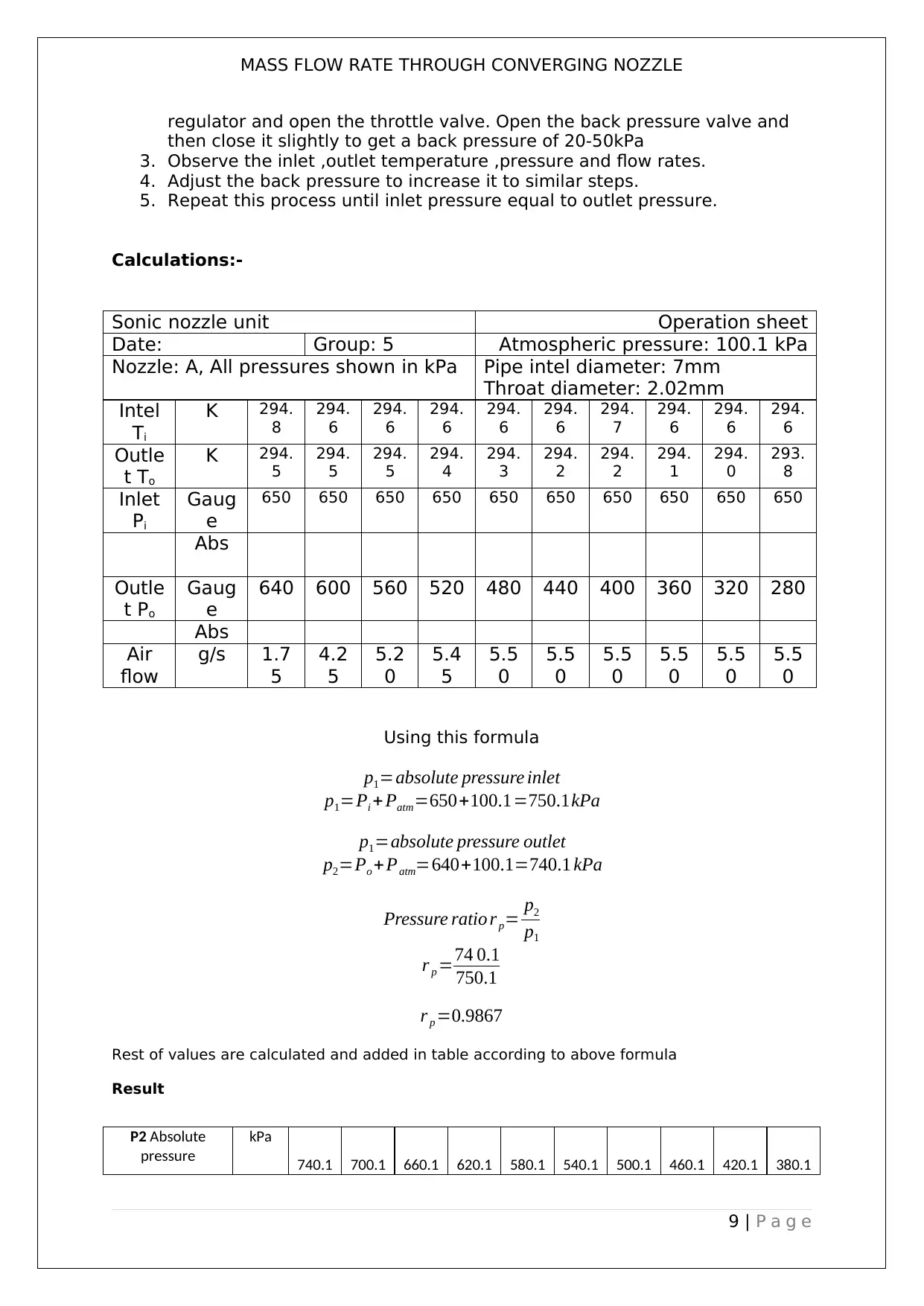
MASS FLOW RATE THROUGH CONVERGING NOZZLE
regulator and open the throttle valve. Open the back pressure valve and
then close it slightly to get a back pressure of 20-50kPa
3. Observe the inlet ,outlet temperature ,pressure and flow rates.
4. Adjust the back pressure to increase it to similar steps.
5. Repeat this process until inlet pressure equal to outlet pressure.
Calculations:-
Sonic nozzle unit Operation sheet
Date: Group: 5 Atmospheric pressure: 100.1 kPa
Nozzle: A, All pressures shown in kPa Pipe intel diameter: 7mm
Throat diameter: 2.02mm
Intel
Ti
K 294.
8
294.
6
294.
6
294.
6
294.
6
294.
6
294.
7
294.
6
294.
6
294.
6
Outle
t To
K 294.
5
294.
5
294.
5
294.
4
294.
3
294.
2
294.
2
294.
1
294.
0
293.
8
Inlet
Pi
Gaug
e
650 650 650 650 650 650 650 650 650 650
Abs
Outle
t Po
Gaug
e
640 600 560 520 480 440 400 360 320 280
Abs
Air
flow
g/s 1.7
5
4.2
5
5.2
0
5.4
5
5.5
0
5.5
0
5.5
0
5.5
0
5.5
0
5.5
0
Using this formula
p1=absolute pressure inlet
p1=Pi +Patm=650+100.1=750.1kPa
p1=absolute pressure outlet
p2=Po +Patm=640+100.1=740.1 kPa
Pressure ratio r p= p2
p1
r p =74 0.1
750.1
r p =0.9867
Rest of values are calculated and added in table according to above formula
Result
P2 Absolute
pressure
kPa
740.1 700.1 660.1 620.1 580.1 540.1 500.1 460.1 420.1 380.1
9 | P a g e
regulator and open the throttle valve. Open the back pressure valve and
then close it slightly to get a back pressure of 20-50kPa
3. Observe the inlet ,outlet temperature ,pressure and flow rates.
4. Adjust the back pressure to increase it to similar steps.
5. Repeat this process until inlet pressure equal to outlet pressure.
Calculations:-
Sonic nozzle unit Operation sheet
Date: Group: 5 Atmospheric pressure: 100.1 kPa
Nozzle: A, All pressures shown in kPa Pipe intel diameter: 7mm
Throat diameter: 2.02mm
Intel
Ti
K 294.
8
294.
6
294.
6
294.
6
294.
6
294.
6
294.
7
294.
6
294.
6
294.
6
Outle
t To
K 294.
5
294.
5
294.
5
294.
4
294.
3
294.
2
294.
2
294.
1
294.
0
293.
8
Inlet
Pi
Gaug
e
650 650 650 650 650 650 650 650 650 650
Abs
Outle
t Po
Gaug
e
640 600 560 520 480 440 400 360 320 280
Abs
Air
flow
g/s 1.7
5
4.2
5
5.2
0
5.4
5
5.5
0
5.5
0
5.5
0
5.5
0
5.5
0
5.5
0
Using this formula
p1=absolute pressure inlet
p1=Pi +Patm=650+100.1=750.1kPa
p1=absolute pressure outlet
p2=Po +Patm=640+100.1=740.1 kPa
Pressure ratio r p= p2
p1
r p =74 0.1
750.1
r p =0.9867
Rest of values are calculated and added in table according to above formula
Result
P2 Absolute
pressure
kPa
740.1 700.1 660.1 620.1 580.1 540.1 500.1 460.1 420.1 380.1
9 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
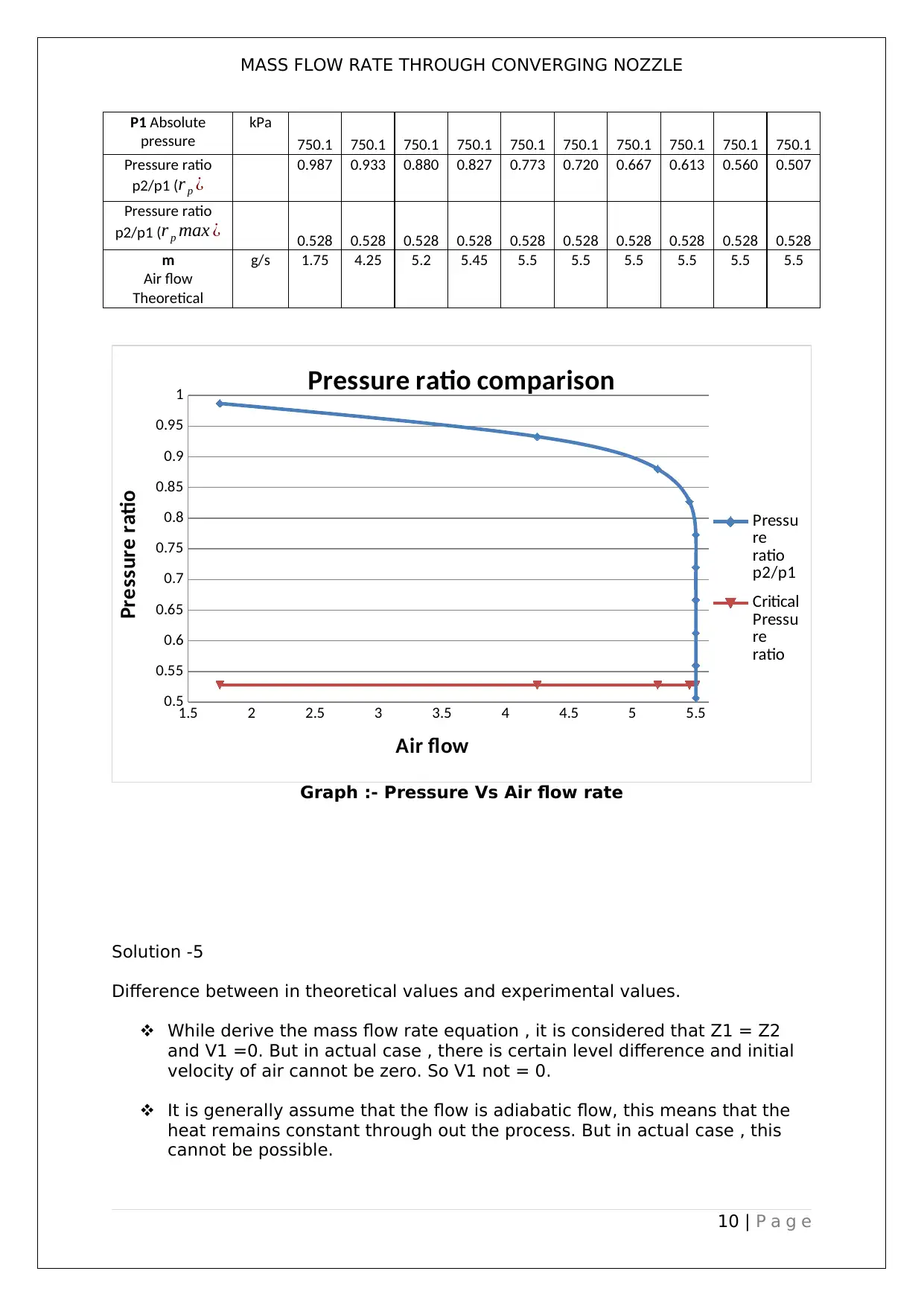
MASS FLOW RATE THROUGH CONVERGING NOZZLE
P1 Absolute
pressure
kPa
750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1
Pressure ratio
p2/p1 (r p ¿
0.987 0.933 0.880 0.827 0.773 0.720 0.667 0.613 0.560 0.507
Pressure ratio
p2/p1 (r p max ¿ 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528
m
Air flow
Theoretical
g/s 1.75 4.25 5.2 5.45 5.5 5.5 5.5 5.5 5.5 5.5
1.5 2 2.5 3 3.5 4 4.5 5 5.5
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1 Pressure ratio comparison
Pressu
re
ratio
p2/p1
Critical
Pressu
re
ratio
Air flow
Pressure ratio
Graph :- Pressure Vs Air flow rate
Solution -5
Difference between in theoretical values and experimental values.
While derive the mass flow rate equation , it is considered that Z1 = Z2
and V1 =0. But in actual case , there is certain level difference and initial
velocity of air cannot be zero. So V1 not = 0.
It is generally assume that the flow is adiabatic flow, this means that the
heat remains constant through out the process. But in actual case , this
cannot be possible.
10 | P a g e
P1 Absolute
pressure
kPa
750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1 750.1
Pressure ratio
p2/p1 (r p ¿
0.987 0.933 0.880 0.827 0.773 0.720 0.667 0.613 0.560 0.507
Pressure ratio
p2/p1 (r p max ¿ 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528 0.528
m
Air flow
Theoretical
g/s 1.75 4.25 5.2 5.45 5.5 5.5 5.5 5.5 5.5 5.5
1.5 2 2.5 3 3.5 4 4.5 5 5.5
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1 Pressure ratio comparison
Pressu
re
ratio
p2/p1
Critical
Pressu
re
ratio
Air flow
Pressure ratio
Graph :- Pressure Vs Air flow rate
Solution -5
Difference between in theoretical values and experimental values.
While derive the mass flow rate equation , it is considered that Z1 = Z2
and V1 =0. But in actual case , there is certain level difference and initial
velocity of air cannot be zero. So V1 not = 0.
It is generally assume that the flow is adiabatic flow, this means that the
heat remains constant through out the process. But in actual case , this
cannot be possible.
10 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

MASS FLOW RATE THROUGH CONVERGING NOZZLE
It is assumed that the V2 velocity is uniform throughout , But in actual
case , environment conditions act on it like friction drag which cause
hindrance to the motion of air.
Many more other environmental condition are assumed to be uniform like
atmospheric pressure, uniform density and other factor like human error,
But these factors are not homogenous in nature.
Reference
Chapter 17_Introduction to compressible flow in “Thermodynamics: an engineering
approach”, Cengel, Y. A. et. al.
Chapter 16_ Compressible flow in “Engineering Thermodynamics”, R.K RAJPUT
11 | P a g e
It is assumed that the V2 velocity is uniform throughout , But in actual
case , environment conditions act on it like friction drag which cause
hindrance to the motion of air.
Many more other environmental condition are assumed to be uniform like
atmospheric pressure, uniform density and other factor like human error,
But these factors are not homogenous in nature.
Reference
Chapter 17_Introduction to compressible flow in “Thermodynamics: an engineering
approach”, Cengel, Y. A. et. al.
Chapter 16_ Compressible flow in “Engineering Thermodynamics”, R.K RAJPUT
11 | P a g e
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





