Functions and Graphs in Mathematics

This assignment focuses on various mathematical concepts related to functions and graphs. It covers topics such as defining functions, identifying domain and range, analyzing graph transformations, determining intervals of increase/decrease, finding intercepts and slopes, and understanding the characteristics of odd and even functions. Students are presented with questions requiring them to apply these concepts to solve problems involving both algebraic and graphical representations of functions.

Question One
A function is a relation in which each element of the domain is paired with exactly one element
of the range.
Domain Range
4 5
6 7
8 8
Since each element of the domain is paired with exactly one element of the range, the relation is
a function.
Question Two
The graph of g is a shifted graph of f, two steps upwards.
Question Three
y is a function of x .
I used the description of domain−range relation¿ confirm.A function is a relation in which each
element of the domain is paired with exactly one element of the range; as illustrated below:
domain Range
-1 1
-2 2
-3 3
-4 4

Question Four
a) a. the function’s domain: −∞ < x <∞
b) b. the function’s range: 1 ≤ y ≤ ∞
c) c. the x-intercepts, if any:¿
d) d. the y-intercept, if any: d=1
e) e. the function’s values f (−1 )and f (3)
f ( −1 ) =2
f ( 3 )=4
Question Five
a) The intervals on which the function is increasing, if any:
The function isincreasing∈the ineterval:−∞ ≤ x <−1
b) The intervals on which the function is decreasing, if any:
The function is decreasing∈the interval:−1< x ≤ ∞
c) The intervals on which the function is constant, if any: The function is constant at x=−1
Question Six
The graph is a graph of odd function. The graph is symmetrical based on the origin.
As illustrated by: ( −1,1 ) , ( 0,0 ) ,(1 ,−1)
Question Seven
a) The domain of f: −∞ ≤ x ≤ ∞
b) The range of f:4 ≤ f (x )≤ ∞
c) The x-intercepts : ¿ 1
d) The y-intercept: ¿ 4
e) Intervals on which f is increasing: 4 < x ≤ ∞
f) Intervals on which f is decreasing :0<x <4
g) Intervals on which f is constant :−∞ ≤ x ≤ 0
h) The number at which f has a relative minimum: x=4
i) The relative minimum of f:f ( x )=−4
j) f(-3) :¿ 4
k) The values of x for which f(x) = -2 : x=2
l) is f even, odd, or neither?: Neither
Question Eight

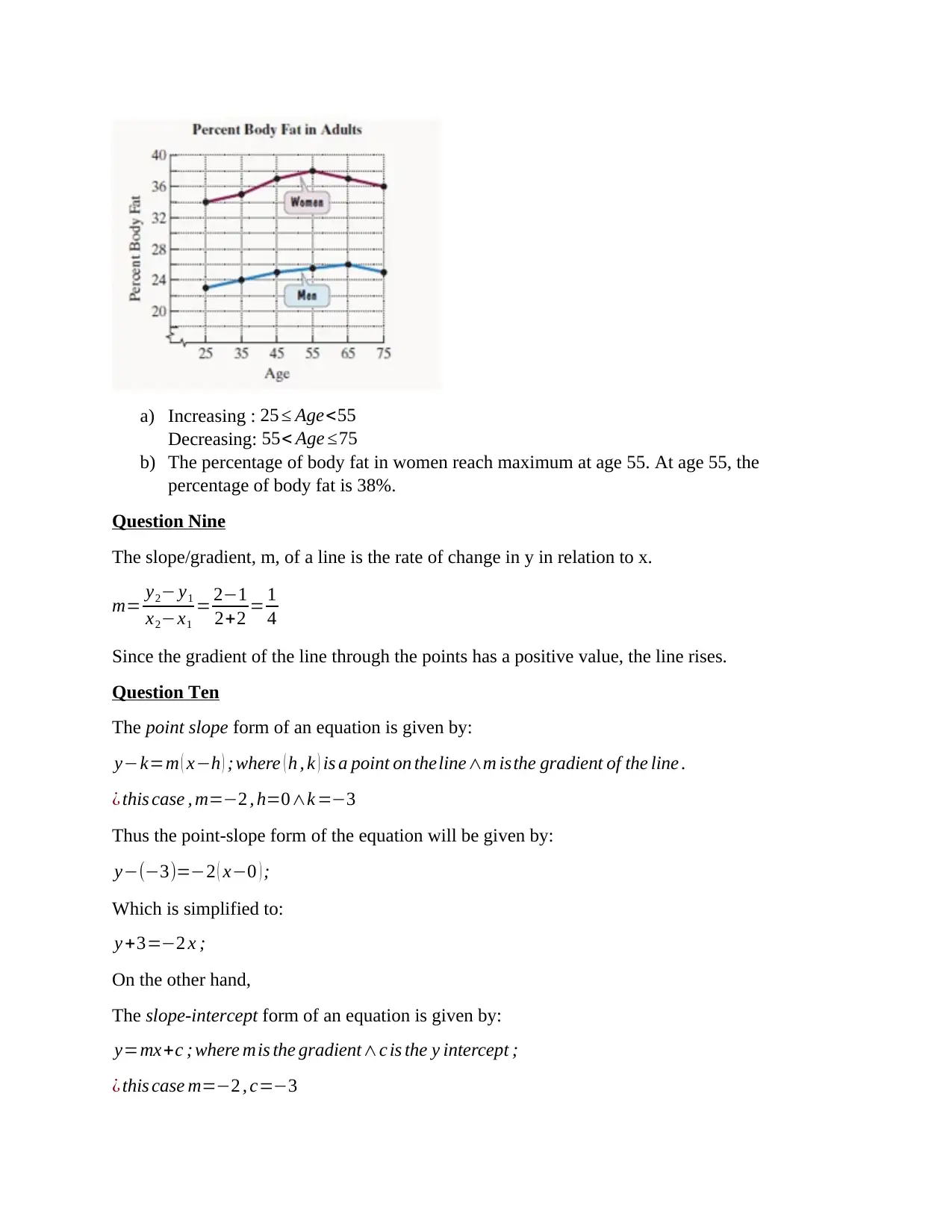
a) Increasing : 25 ≤ Age<55
Decreasing: 55< Age ≤75
b) The percentage of body fat in women reach maximum at age 55. At age 55, the
percentage of body fat is 38%.
Question Nine
The slope/gradient, m, of a line is the rate of change in y in relation to x.
m= y2− y1
x2−x1
= 2−1
2+2 = 1
4
Since the gradient of the line through the points has a positive value, the line rises.
Question Ten
The point slope form of an equation is given by:
y−k=m ( x−h ) ; where ( h , k ) is a point on theline∧m isthe gradient of the line .
¿ this case , m=−2 , h=0∧k =−3
Thus the point-slope form of the equation will be given by:
y−(−3)=−2 ( x−0 ) ;
Which is simplified to:
y +3=−2 x ;
On the other hand,
The slope-intercept form of an equation is given by:
y=mx+c ; where mis the gradient∧c is the y intercept ;
¿ this case m=−2 , c=−3

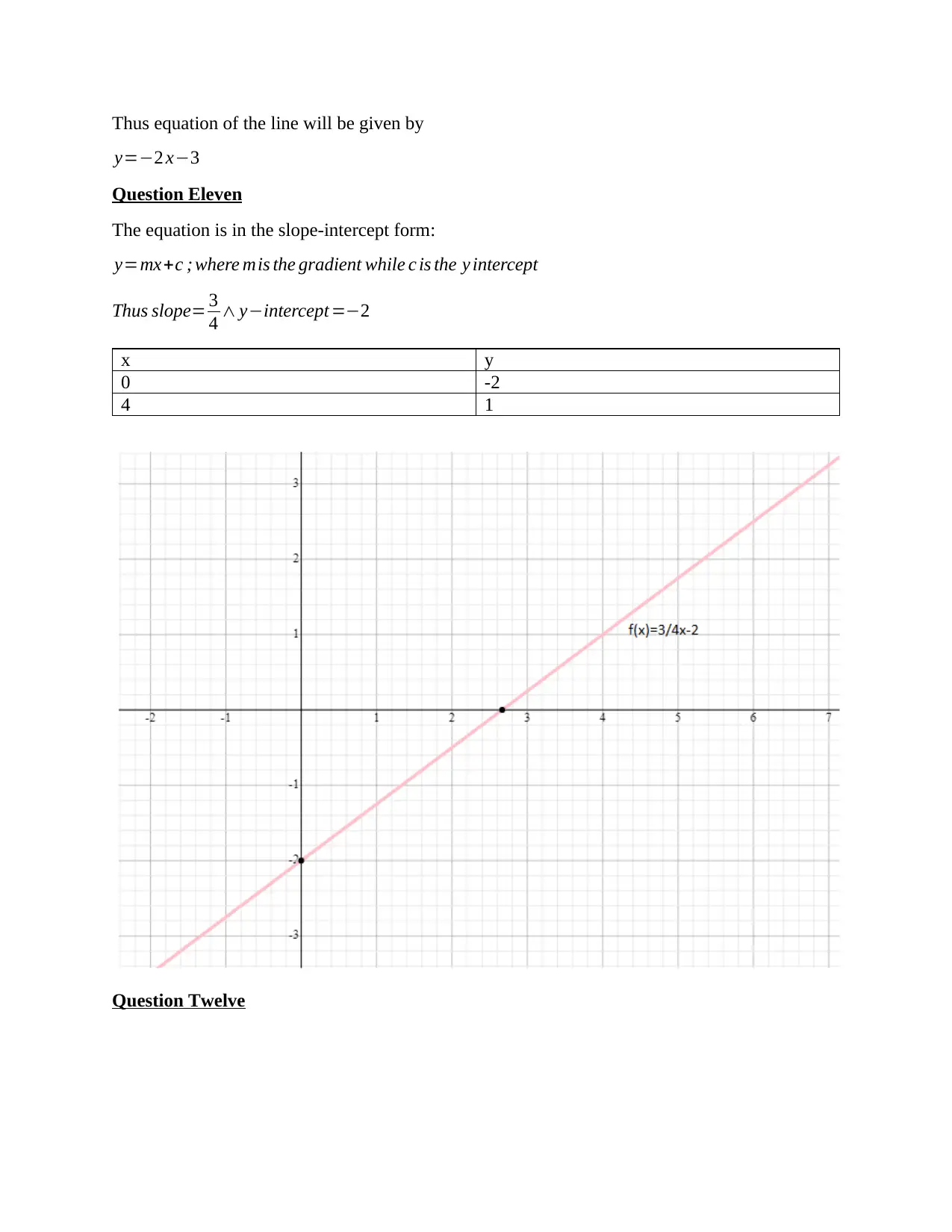
Thus equation of the line will be given by
y=−2 x−3
Question Eleven
The equation is in the slope-intercept form:
y=mx+c ; where mis the gradient while c is the y intercept
Thus slope= 3
4 ∧ y−intercept =−2
x y
0 -2
4 1
Question Twelve

Largest Slope: m1
Second Largest: m3
Second Smallest: m4
Smallest Slope: m2
Question Thirteen
Since L∧ y=−2 x are∥, they have the same gradient .
slope of y =−2 x=−2
Thus gradient of L ¿−2∧ point (3,4 ) lies on L
The point slope form of an equation is given by:
y−k=m ( x−h ) ; where ( h , k ) is a point on theline∧m isthe gradient of the line .
¿ this case , m=−2 , h=3∧k =4
Thus the point-slope form of the equation will be given by:
y−(4 )=−2 ( x−3 ) ;
Which is simplified to:
y−4=−2(x−3) ;
On the other hand,
The slope-intercept form of an equation is given by:
y=mx+c ; where mis the gradient∧c is the y intercept ;

¿ this case m=−2 , c=?
From y−4=−2 ( x−3 ) above , when x=0 ,
y−4=−2 ( 0−3 )
y=6+4=10
Thus y−intercept =10 ; c=10
Thus equation of the line will be given by
y=−2 x +10
Question Fourteen
f ( x )=x2 +2 x
At x1 , f ( x )=32 +2∗3=15
At x2 , f ( x ) =52 +2∗5=35
Consequently , thw two points are ( 3,15 ) ∧(5 , 35)
Average rate of change of a function between ( x1 , y1 ) ∧ ( x2 , y2 )= y2− y1
x2−x1
¿ 35−15
5−3 = 20
2 =10
Thus average Change=10 Units
Question Fifteen
The two points on theline which is perpendicular ¿ f are ( 2,0 ) ∧ ( 0 ,−4 )
Slopeof the line= y2− y1
x2−x1
= ( −4
−2 )=2
Given two slopes of perpendicular lines , m1∧m2 ; m1=−1
m2
Thus slope of f =−1
2
The slope-intercept form of an equation is given by:
y=mx+c ; where mis the gradient∧c is the y intercept ;
¿ this case m=−1
2 , c=−4
Thus equation of the line will be given by

y=−1
2 x−4
Question Sixteen
Percentage of Total Spending on food:
In 1950, Americans spent 22% of their budget on food. This has decreased at an average rate of
approximately 0.25% per year since then
Since it is a decrease, the slope is negative hence −0.25
When x=0 , p ( x ) =22
Hence p ( x )=−0.25 x+ 22
Percentage of Total Spending on Health Care:

In 1950, Americans spent 3% of their budget on healthcare. This has increased at an average rate
of approximately 0.22% per year since then
Since it is an increase, the slope is positive hence −0.21667
When x=0 , p ( x )=3
Hence p ( x )=−0.21667 x +3
Question Seventeen
Question Eighteen
Question Nineteen

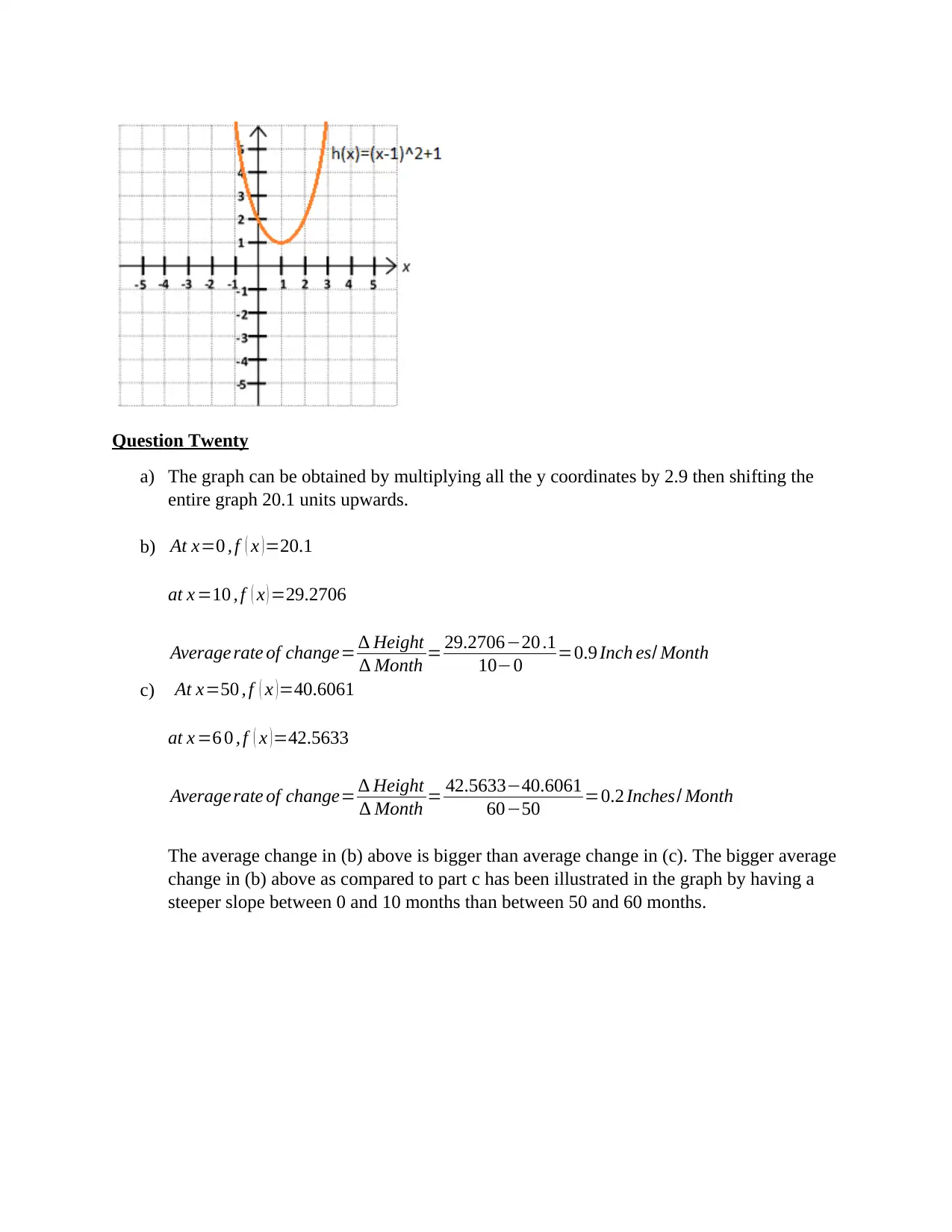
Question Twenty
a) The graph can be obtained by multiplying all the y coordinates by 2.9 then shifting the
entire graph 20.1 units upwards.
b) At x=0 , f ( x ) =20.1
at x =10 , f ( x ) =29.2706
Average rate of change= ∆ Height
∆ Month = 29.2706−20 .1
10−0 =0.9 Inch es/ Month
c) At x=50 , f ( x ) =40.6061
at x =6 0 , f ( x ) =42.5633
Average rate of change= ∆ Height
∆ Month = 42.5633−40.6061
60−50 =0.2 Inches/ Month
The average change in (b) above is bigger than average change in (c). The bigger average
change in (b) above as compared to part c has been illustrated in the graph by having a
steeper slope between 0 and 10 months than between 50 and 60 months.