MAT4MDS Assignment 2, 2019: Solving Equations, Graphing, and Proofs

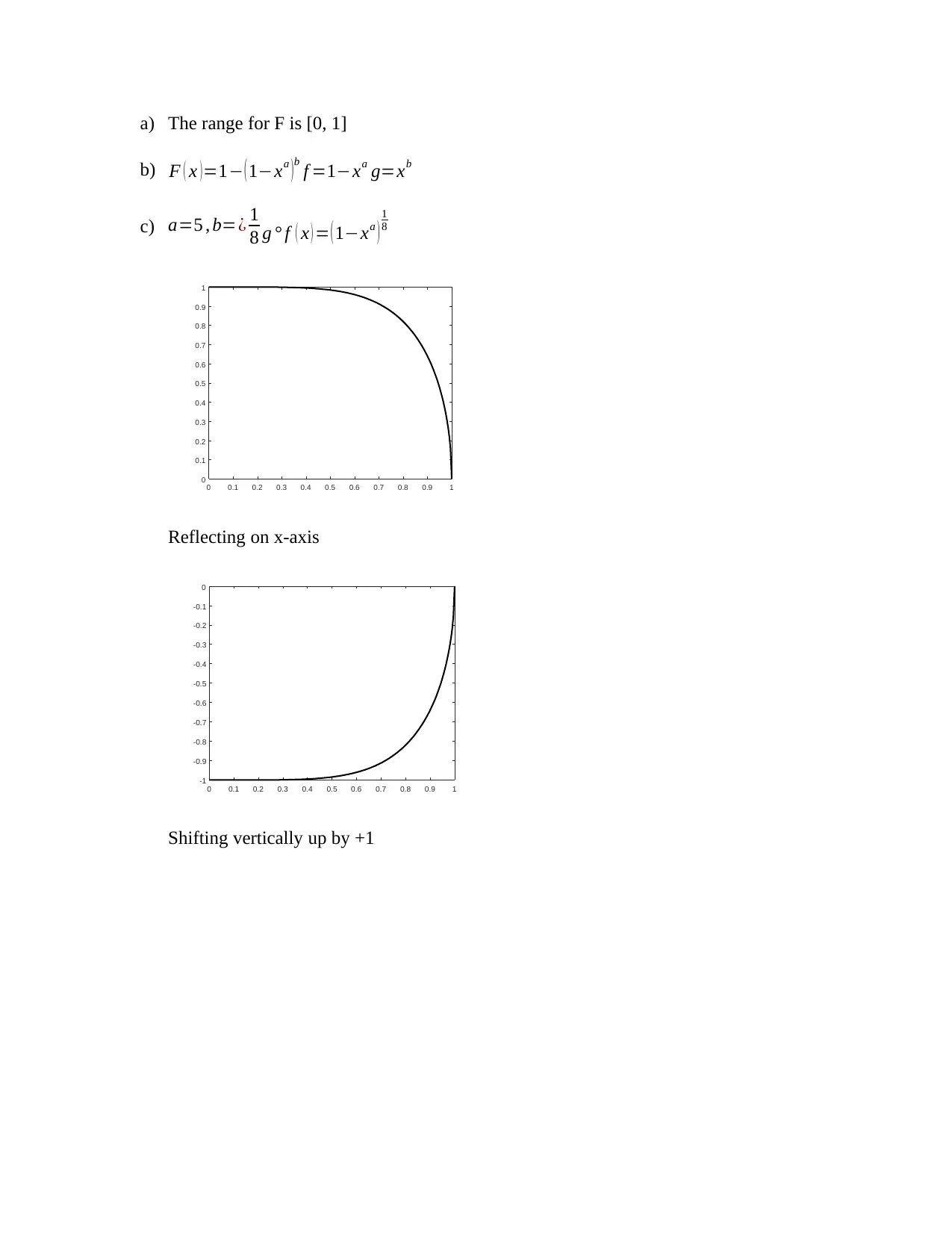
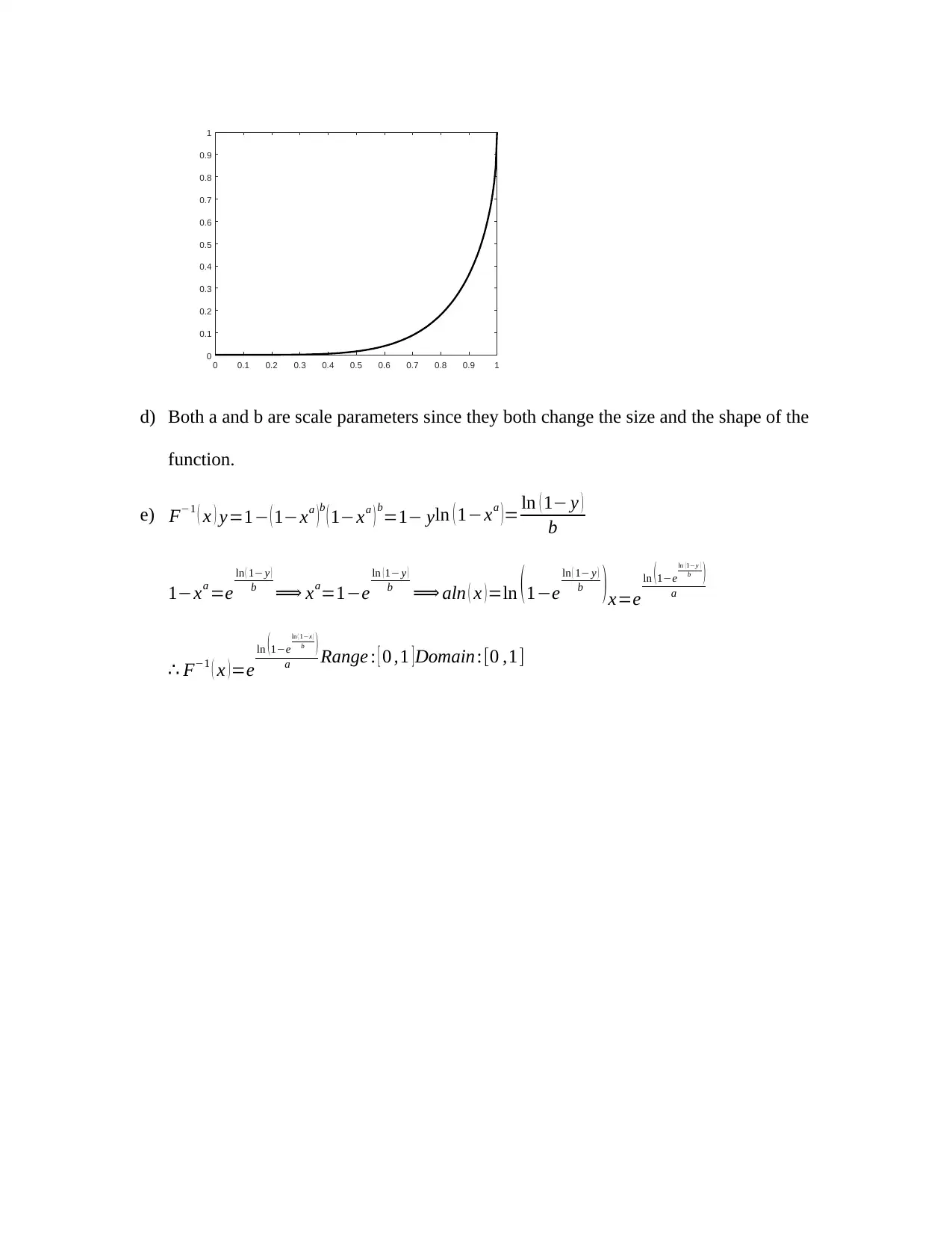
This document provides comprehensive solutions for MAT4MDS Assignment 2, covering a range of mathematical concepts. The solutions include detailed steps for solving logarithmic and exponential equations, such as loge(loge(3x)) = 0, ex^2 −5x+6 = 1, log3(x^2 − 9) − log3(x + 3) = 2 − log3(x + 1), and 9x − 2·3x+1 = 7. The assignment also involves proving mathematical identities like logb(a) loga(b) = 1 and log 1 (x) = − logb (x). Furthermore, the document provides solutions for graphing functions such as y = x, ( 51 )x , ( 1c )x on the same axes, and estimating the slope of a logarithmic graph. Additionally, the assignment explores function analysis including the range, scale parameters, and the inverse of a given function F(x) = 1−( 1−x a ) and f =1−x a g=x b.

MAT4MDS ASSIGNMENT 2, 2019
Question 1
a) Solving these equations for x
i) loge ( log e ( 3 x ) ) =0 applying the log rule 0=ln ( e0 )=ln ( 1 )
loge ( log e ( 3 x ) ) =ln ( 1 )loge ( 3 x ) =1e1=3 x ⟹ x= e1
3
ii) ex2−5 x +6=1 ln (ex2−5 x+6 )=ln ( 1 ) x2−5 x+6=0solving the quadratic equation
( x−3 ) ( x−2 ) =0 ∴ x=3 , x=2
iii) log3 ( x2−9 )−log3 ( x +3 ) =2−log3 ( x+1 )log3 ( x2−9 )−log3 ( x +3 ) +log3 ( x+ 1 ) =2
log3 ( ( x2−9 ) ( x +1 )
( x+3 ) )=232= ( x +3 ) ( x−3 ) ( x+1 )
( x+3 ) ⟹ ( x−3 ) ( x +1 )=9 x2−2 x−12=0
∴ x=1+ √ 13∨x=1+ √13 x=4.605551275∨x=−2.605551275 in decimal format
iv) 9x−2.3x+1=7
Using trial and error method x=1.17083
b) Proof
i) log a ( b ) logb ( a ) =1logb ( a )= 1
loga b 1= 1
loga b × 1
logb a × ( loga ( b ) logb ( a ) )
1= ( 1
loga b × loga ( b ) )× ( 1
logb a × logb ( a ) )1=1 ×1=1
ii) log 1
b
( x )=−logb ( x ) logb−1 ( x )=−logb ( x ) use of change of base rule ln ( x )
ln ( b−1 ) =−ln ( x )
ln ( b )
ln ( x )
−ln ( b ) =−ln ( x )
ln ( b )
ln ( x )
ln ( b ) =−ln ( x )
ln ( b )
c) Graphing the following equations on the same axis, c=8

y=x , ( 1
5 ) x
, ( 1
8 )
x
-1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4
x
-1
0
1
2
3
4
5
6
7
8
9
y
y=x, (1/5)x, (1/c)x c=9
y=x
y=(1/5)x
y=(1/c)x
d) Estimating the slope of the red line
The graph is logarithmic on y-axis
s= ∆ y
∆ x = ∆ W
∆ n at ( 1,1 ) ∧(2,10)
Where W total number of websites, and n the number of year s= ∆ W
∆ n = 1
2−1 =1 ∆ W =1for
one log cycle
∴ s=1 yintercept =−10Thus , y=−10 ( 10 ) x
The relationship between W and n is Exponential relationship
Question 2
F : [ 0 , 1 } → R F ( x )=1− ( 1−xa )b

a) The range for F is [0, 1]
b) F ( x ) =1− ( 1−xa ) b
f =1−xa g=xb
c) a=5 , b=¿ 1
8 g ° f ( x ) = ( 1−xa )
1
8
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Reflecting on x-axis
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-1
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
Shifting vertically up by +1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
d) Both a and b are scale parameters since they both change the size and the shape of the
function.
e) F−1 ( x ) y=1− (1−xa )b
( 1−xa ) b
=1− yln ( 1−xa )= ln ( 1− y )
b
1−xa =e
ln ( 1− y )
b ⟹ xa=1−e
ln (1− y )
b ⟹ aln ( x )=ln (1−e
ln ( 1− y )
b ) x=e
ln ( 1−e
ln (1−y )
b )
a
∴ F−1 ( x ) =e
ln ( 1−e
ln ( 1−x )
b )
a Range : [ 0 ,1 ] Domain:[0 ,1]