MAT9004 Practice Exam Assignment PDF
VerifiedAdded on 2021/05/30
|8
|859
|85
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

MAT9004 Practice Exam
MAT9004 Practice Exam
Institution Name
Student Name
Date
MAT9004 Practice Exam
Institution Name
Student Name
Date
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

MAT9004 Practice Exam
1. f ( x )=−2 x3−9 x2−12 x+ 2
a. f 1 ( x) is the derivative of f (x) with respect to x
using thepower rule, subtraction and additional rule we obtain
f 1 ( x ) =−6 x2−18 x−12
For x ∈[−2,3]
b. f 1 ( x ) =−6 x2−18 x−12
f 11(x ) is the derivative of f 1 ( x ) with respect to x
Using the power rule, addition and the subtraction rule we obtain
f 11 ( x )=−12 x
Since x ∈[−2,3] then
f 11 ( x )=−12 x for x ∈[−2,3]
c. The stationery points are at point f 1 ( x )=0
Hence the stationery points will be at the roots of −6 x2−18 x−12
Using the quadratic equation x=−b ± √ b2−4 ac
2 a
We obtain the roots of the function at the points x=−1∧−2
The value of f ( x ) at the stationery points will be
f ( −1 ) =7∧f ( −2 ) =6
d. Finding local minimum and local maximum
The stationery points are at (−1,7 )∧(−2,6)
Now we use the sign test to determine if the points are maximum or minimum
x -2 -1 0
f 1 ( x) 0 -12
sign +ve -ve
Using -2 and 0 to do the sign test we can see that the sign changes from positive
to negative. When the sign changes from positive to negative, then this indicates
that we have a local maximum. Hence point (-1,7) is a local maximum point.
Now using the test sign, we test point (-2,6) using the values -2 and 0
x -3 -2 -1
1. f ( x )=−2 x3−9 x2−12 x+ 2
a. f 1 ( x) is the derivative of f (x) with respect to x
using thepower rule, subtraction and additional rule we obtain
f 1 ( x ) =−6 x2−18 x−12
For x ∈[−2,3]
b. f 1 ( x ) =−6 x2−18 x−12
f 11(x ) is the derivative of f 1 ( x ) with respect to x
Using the power rule, addition and the subtraction rule we obtain
f 11 ( x )=−12 x
Since x ∈[−2,3] then
f 11 ( x )=−12 x for x ∈[−2,3]
c. The stationery points are at point f 1 ( x )=0
Hence the stationery points will be at the roots of −6 x2−18 x−12
Using the quadratic equation x=−b ± √ b2−4 ac
2 a
We obtain the roots of the function at the points x=−1∧−2
The value of f ( x ) at the stationery points will be
f ( −1 ) =7∧f ( −2 ) =6
d. Finding local minimum and local maximum
The stationery points are at (−1,7 )∧(−2,6)
Now we use the sign test to determine if the points are maximum or minimum
x -2 -1 0
f 1 ( x) 0 -12
sign +ve -ve
Using -2 and 0 to do the sign test we can see that the sign changes from positive
to negative. When the sign changes from positive to negative, then this indicates
that we have a local maximum. Hence point (-1,7) is a local maximum point.
Now using the test sign, we test point (-2,6) using the values -2 and 0
x -3 -2 -1
MAT9004 Practice Exam
f 1 ( x) -2 0
sign -ve +ve
The sign is changing from negative to positive hence the point (-2,6) is a local
minimum.
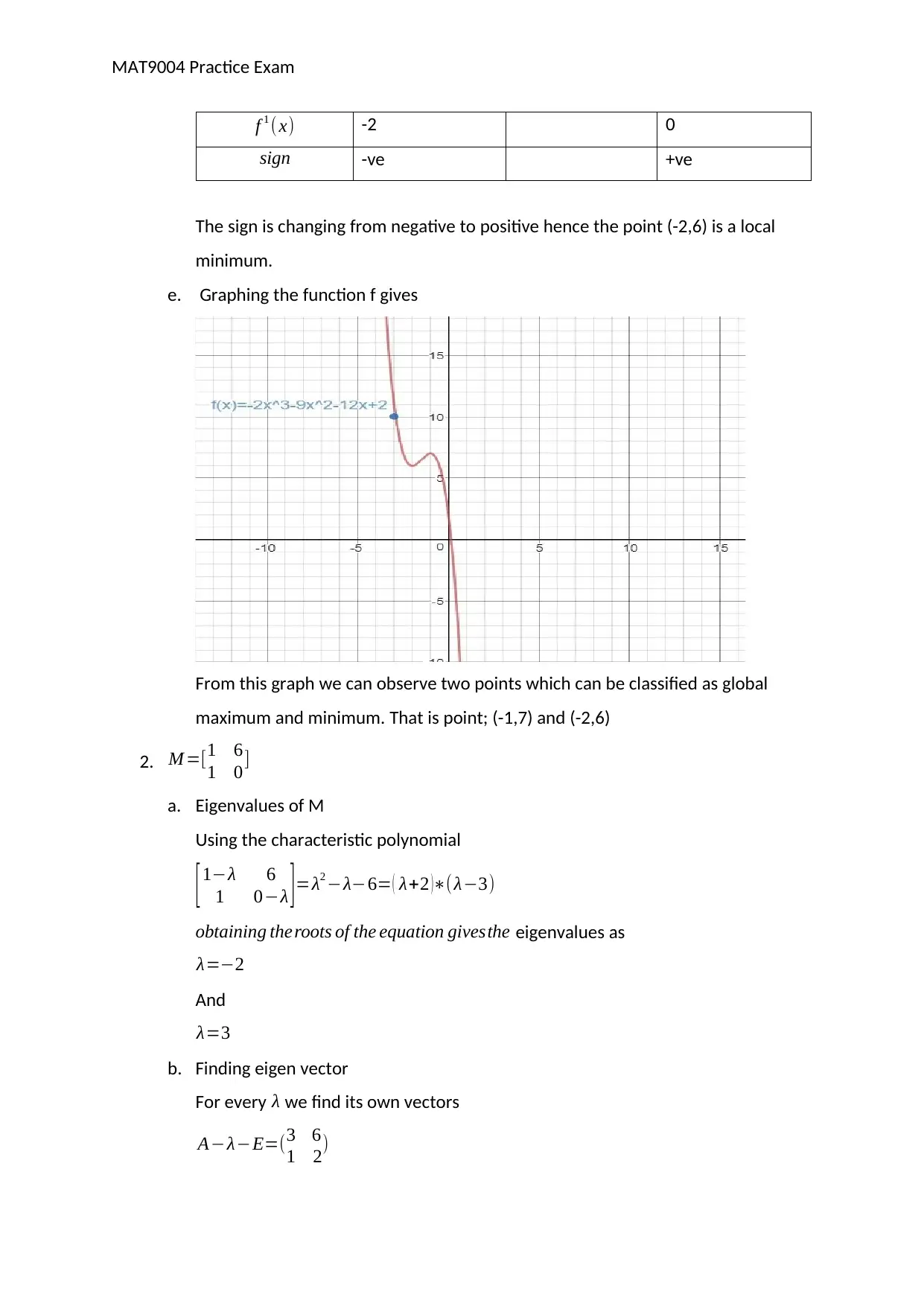
e. Graphing the function f gives
From this graph we can observe two points which can be classified as global
maximum and minimum. That is point; (-1,7) and (-2,6)
2. M =[1 6
1 0]
a. Eigenvalues of M
Using the characteristic polynomial
[ 1−λ 6
1 0−λ ] =λ2 −λ−6= ( λ+2 )∗(λ−3)
obtaining the roots of the equation givesthe eigenvalues as
λ=−2
And
λ=3
b. Finding eigen vector
For every λ we find its own vectors
A−λ−E=(3 6
1 2)
f 1 ( x) -2 0
sign -ve +ve
The sign is changing from negative to positive hence the point (-2,6) is a local
minimum.
e. Graphing the function f gives
From this graph we can observe two points which can be classified as global
maximum and minimum. That is point; (-1,7) and (-2,6)
2. M =[1 6
1 0]
a. Eigenvalues of M
Using the characteristic polynomial
[ 1−λ 6
1 0−λ ] =λ2 −λ−6= ( λ+2 )∗(λ−3)
obtaining the roots of the equation givesthe eigenvalues as
λ=−2
And
λ=3
b. Finding eigen vector
For every λ we find its own vectors
A−λ−E=(3 6
1 2)

MAT9004 Practice Exam
A−λE=0, so, we have a homogeneous system of linear equations we solve it by
Gaussian Elimination
(3 6 0
1 2 0 )¿1/ 3
R1 /3 → R1
( 1 2 0
1 2 0 ) ↲∗(−1)
R2−1∗R1 → R2 (1 2
0 0)
{x1 +2 x2=0 (1)
Find the variables x1from the equation of the system (1)
x1=−2 x2
X =(−2 x 2
x 2 )
let x2 =1 , v1 =(−2
1 )
2 λ 2=3
A−λ∗E=(−2 6
1 −3)
A−λ∗E=0, so, we have a homogeneous system of linear equations, we solve it
by Gaussian Elimination to obtain
{x1−3 x2=0 (1)
let x2 =1, then v2=(3
1)
c. Diagonalize M
The diagonal matrix (the diagonal entries are the eigenvalues −λ1 , λ2
D=(−2 0
0 3)
The matrix with the eigenvectors ( v1 , v2 ¿ as its columns
P=(−2 3
0 3)
then P−1=(−1 /5 3/5
1 /5 2/5)
A=P−1∗D∗P
A−λE=0, so, we have a homogeneous system of linear equations we solve it by
Gaussian Elimination
(3 6 0
1 2 0 )¿1/ 3
R1 /3 → R1
( 1 2 0
1 2 0 ) ↲∗(−1)
R2−1∗R1 → R2 (1 2
0 0)
{x1 +2 x2=0 (1)
Find the variables x1from the equation of the system (1)
x1=−2 x2
X =(−2 x 2
x 2 )
let x2 =1 , v1 =(−2
1 )
2 λ 2=3
A−λ∗E=(−2 6
1 −3)
A−λ∗E=0, so, we have a homogeneous system of linear equations, we solve it
by Gaussian Elimination to obtain
{x1−3 x2=0 (1)
let x2 =1, then v2=(3
1)
c. Diagonalize M
The diagonal matrix (the diagonal entries are the eigenvalues −λ1 , λ2
D=(−2 0
0 3)
The matrix with the eigenvectors ( v1 , v2 ¿ as its columns
P=(−2 3
0 3)
then P−1=(−1 /5 3/5
1 /5 2/5)
A=P−1∗D∗P
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

MAT9004 Practice Exam
(−1
5
3
5
1
5
2
5 )∗(−2 0
0 3 )∗(−2 3
0 3 )=(
−4
5
33
5
4
5
12
5
)
3. Calculate probability
f ( x )=x5 + x2 + x, (xϵ [ 0,1]
probability of {x> 1
2 }=∫
1/ 5
1
x5 + x2 + x= [ 1
6 + 1
3 + 1
2 ] − [ 1
384 + 1
2 + 1
8 ]= 319
384
4. The profit function is
p ( a , b )=a b2−a2 +b2 +6 b−9 a+10
The optimal points are at the derivative of the profit function equals to zero.
The derivative with respect to b gives
¿ 2 ab+2 b+6=0
¿
The derivative with respect to a
b2−2 a−9=0
Now a= b2−9
2
Now 2∗b2−9
2 +2 b+6
¿ b2 +2 b−3=0
using thequadratic formulawe obtain b¿−3 amd 1
Since the value of b is minimum we take -3
This gives the value of a¿ b2−9
2 =0
5. Not divisible by 2 and not divisible by 5.
a. This means the last digit cannot be 0,2,4,6,8
Now we must pick 4 digits from a bucket of 10
This can be picked in the following way
The fist number can be picked in 9 ways
2nd in 10 ways
3rd in 10 ways
4th in 4 ways
(−1
5
3
5
1
5
2
5 )∗(−2 0
0 3 )∗(−2 3
0 3 )=(
−4
5
33
5
4
5
12
5
)
3. Calculate probability
f ( x )=x5 + x2 + x, (xϵ [ 0,1]
probability of {x> 1
2 }=∫
1/ 5
1
x5 + x2 + x= [ 1
6 + 1
3 + 1
2 ] − [ 1
384 + 1
2 + 1
8 ]= 319
384
4. The profit function is
p ( a , b )=a b2−a2 +b2 +6 b−9 a+10
The optimal points are at the derivative of the profit function equals to zero.
The derivative with respect to b gives
¿ 2 ab+2 b+6=0
¿
The derivative with respect to a
b2−2 a−9=0
Now a= b2−9
2
Now 2∗b2−9
2 +2 b+6
¿ b2 +2 b−3=0
using thequadratic formulawe obtain b¿−3 amd 1
Since the value of b is minimum we take -3
This gives the value of a¿ b2−9
2 =0
5. Not divisible by 2 and not divisible by 5.
a. This means the last digit cannot be 0,2,4,6,8
Now we must pick 4 digits from a bucket of 10
This can be picked in the following way
The fist number can be picked in 9 ways
2nd in 10 ways
3rd in 10 ways
4th in 4 ways

MAT9004 Practice Exam
Hence the total prime like numbers between 1000 and 9999 is
9∗10∗10∗4=3600
b. Has at least one even digit
Here we select 4 numbers from a bucket of 10 in the following way
1st number 9 ways
2nd number 10 ways
3rd number 10ways
4th number 5 ways
Now let’s assume that the even digit is in the 1st number then the numbers will
be
4∗5∗5∗4=400
Leta now assume the even number is in the second digit
5∗5∗5∗4=500
Let’s assume the even number is in the 3rd digit
5∗5∗5∗4=500
The even digit cannot be in the fourth number as this will make the number
prime like anymore
In total the numbers are 400+ 500+500=1400
c. Prime like numbers not divisible by 3
Here we must choose the four numbers such that the sum of the digit is not
divisible by 3
1st digit 9 ways
2nd digit 10 ways
3rd digit 10 ways
4th digit 3 ways
The numbers are 9∗10∗10∗3=2700
6. Y uniformly distributed
a.
For u1
Y -1 0 1 2
Hence the total prime like numbers between 1000 and 9999 is
9∗10∗10∗4=3600
b. Has at least one even digit
Here we select 4 numbers from a bucket of 10 in the following way
1st number 9 ways
2nd number 10 ways
3rd number 10ways
4th number 5 ways
Now let’s assume that the even digit is in the 1st number then the numbers will
be
4∗5∗5∗4=400
Leta now assume the even number is in the second digit
5∗5∗5∗4=500
Let’s assume the even number is in the 3rd digit
5∗5∗5∗4=500
The even digit cannot be in the fourth number as this will make the number
prime like anymore
In total the numbers are 400+ 500+500=1400
c. Prime like numbers not divisible by 3
Here we must choose the four numbers such that the sum of the digit is not
divisible by 3
1st digit 9 ways
2nd digit 10 ways
3rd digit 10 ways
4th digit 3 ways
The numbers are 9∗10∗10∗3=2700
6. Y uniformly distributed
a.
For u1
Y -1 0 1 2

MAT9004 Practice Exam
u1 2 0 0 2
Since Y is uniformly distributed all the values occur with equal probability the
expected value of expected value of u1= 2+0+0+2
4 =1
For u2
Y -1 0 1 2
u2 0 0.5 0 0.5
Since all the values occur with uniform probability the expected value will be
0+0.5+0+0.5
4 =0.25
b. Variance of u1=∑
u1
( u1−μ ) p(u1 )
( 2−1 )+ ( 0−1 ) + ( 0−1 ) + ( 2−1 ) = 0
4 =0
The variance is 0
Variance of u2
( 0−0.25 ) + ( 5−0.25 ) + ( 0−0.25 ) + ( 0.5−0.25 )= 0
4 =0
The variance is 0
c. Testing independence of u1 and u2
No, the equations are dependent as they share similar variance
7. A fair 6-sided dice is rolled 3 times
a. Probability that sum is 8
Possible outcomes are 63 =216
Each roll must have a value between 1 and 6
1+1+1=3 cannot be
2+2+2=6 cannot be
3+3+3=9 cannot be
The only way we can have a sum of 8 is ( 3,3,2 ) , ( 4,2,2 ) , ( 6,1,1 ) , ( 5,2,1 )
The roll is 3 times so there are 3∗4=12 possibilities
Thus, the probability is 12
216 =1/18
b. Probability of 1 given sum of 8
u1 2 0 0 2
Since Y is uniformly distributed all the values occur with equal probability the
expected value of expected value of u1= 2+0+0+2
4 =1
For u2
Y -1 0 1 2
u2 0 0.5 0 0.5
Since all the values occur with uniform probability the expected value will be
0+0.5+0+0.5
4 =0.25
b. Variance of u1=∑
u1
( u1−μ ) p(u1 )
( 2−1 )+ ( 0−1 ) + ( 0−1 ) + ( 2−1 ) = 0
4 =0
The variance is 0
Variance of u2
( 0−0.25 ) + ( 5−0.25 ) + ( 0−0.25 ) + ( 0.5−0.25 )= 0
4 =0
The variance is 0
c. Testing independence of u1 and u2
No, the equations are dependent as they share similar variance
7. A fair 6-sided dice is rolled 3 times
a. Probability that sum is 8
Possible outcomes are 63 =216
Each roll must have a value between 1 and 6
1+1+1=3 cannot be
2+2+2=6 cannot be
3+3+3=9 cannot be
The only way we can have a sum of 8 is ( 3,3,2 ) , ( 4,2,2 ) , ( 6,1,1 ) , ( 5,2,1 )
The roll is 3 times so there are 3∗4=12 possibilities
Thus, the probability is 12
216 =1/18
b. Probability of 1 given sum of 8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
MAT9004 Practice Exam
¿ pre (∑ 8∧1 )
prob (∑ ¿ 8 ) =
3
216
1
18 =1/4
8.
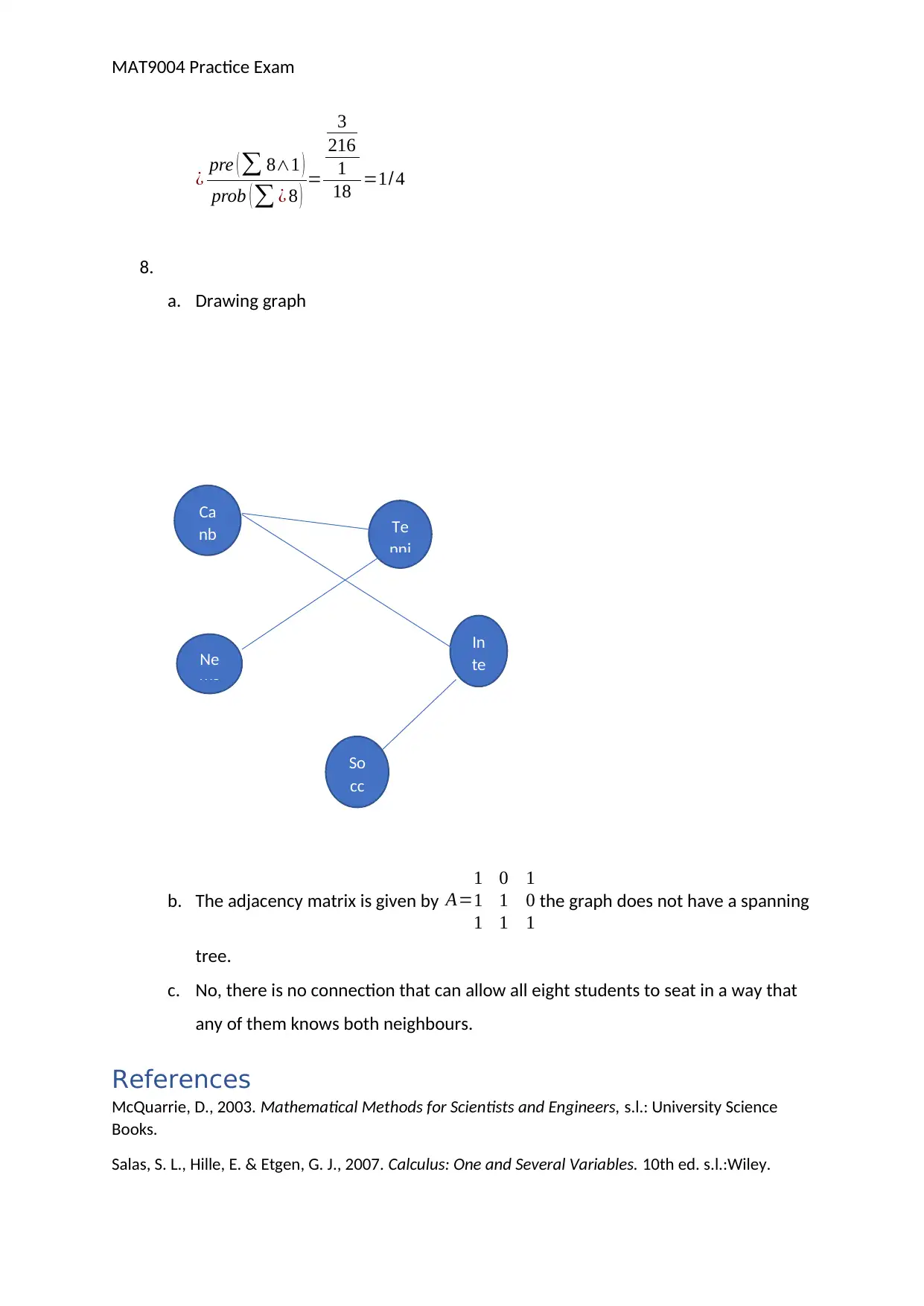
a. Drawing graph
b. The adjacency matrix is given by A=
1 0 1
1 1 0
1 1 1
the graph does not have a spanning
tree.
c. No, there is no connection that can allow all eight students to seat in a way that
any of them knows both neighbours.
References
McQuarrie, D., 2003. Mathematical Methods for Scientists and Engineers, s.l.: University Science
Books.
Salas, S. L., Hille, E. & Etgen, G. J., 2007. Calculus: One and Several Variables. 10th ed. s.l.:Wiley.
Ca
nb Te
nni
Ne
wc
In
te
So
cc
¿ pre (∑ 8∧1 )
prob (∑ ¿ 8 ) =
3
216
1
18 =1/4
8.
a. Drawing graph
b. The adjacency matrix is given by A=
1 0 1
1 1 0
1 1 1
the graph does not have a spanning
tree.
c. No, there is no connection that can allow all eight students to seat in a way that
any of them knows both neighbours.
References
McQuarrie, D., 2003. Mathematical Methods for Scientists and Engineers, s.l.: University Science
Books.
Salas, S. L., Hille, E. & Etgen, G. J., 2007. Calculus: One and Several Variables. 10th ed. s.l.:Wiley.
Ca
nb Te
nni
Ne
wc
In
te
So
cc
1 out of 8
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.