MATH 070 - Homework: Equation Solving and Expression Simplification

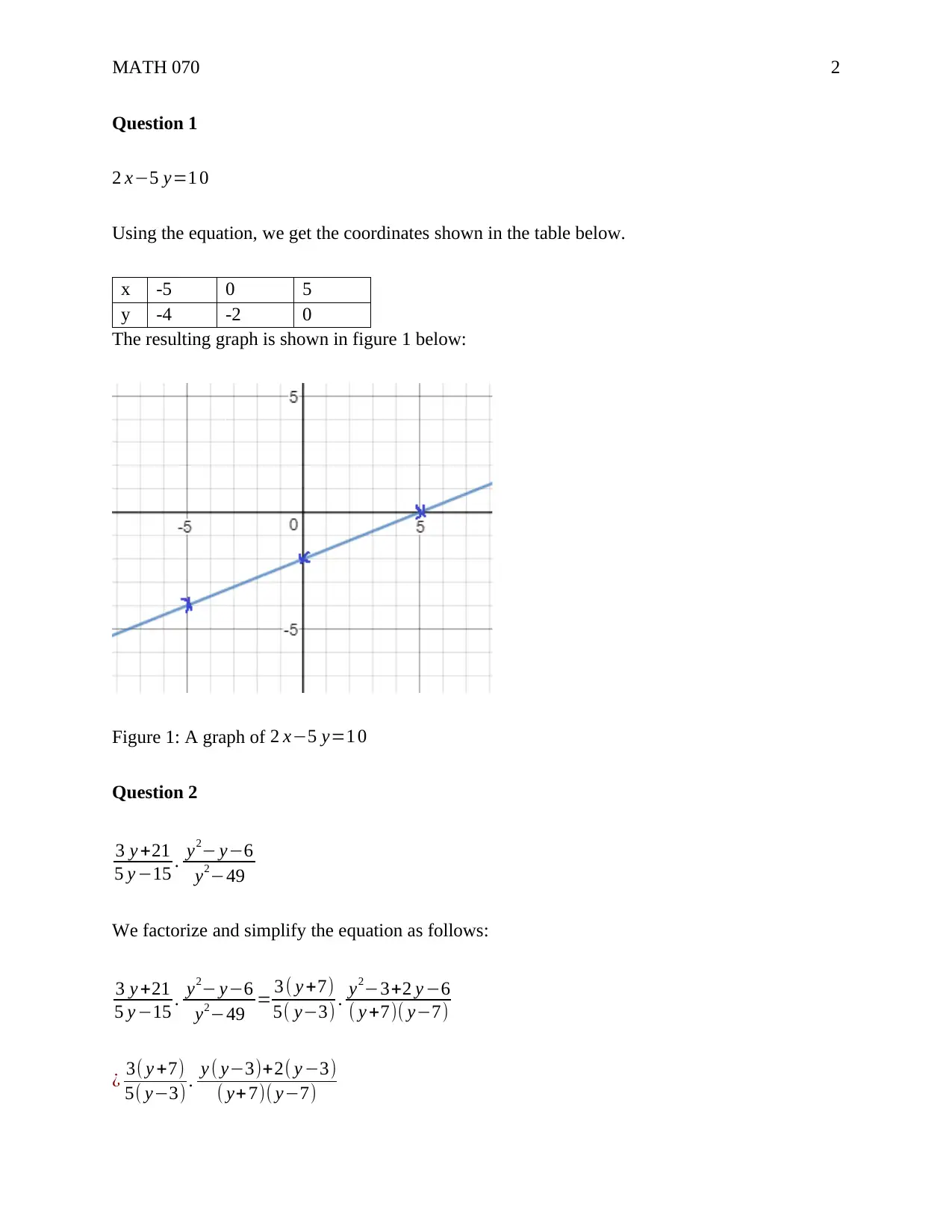
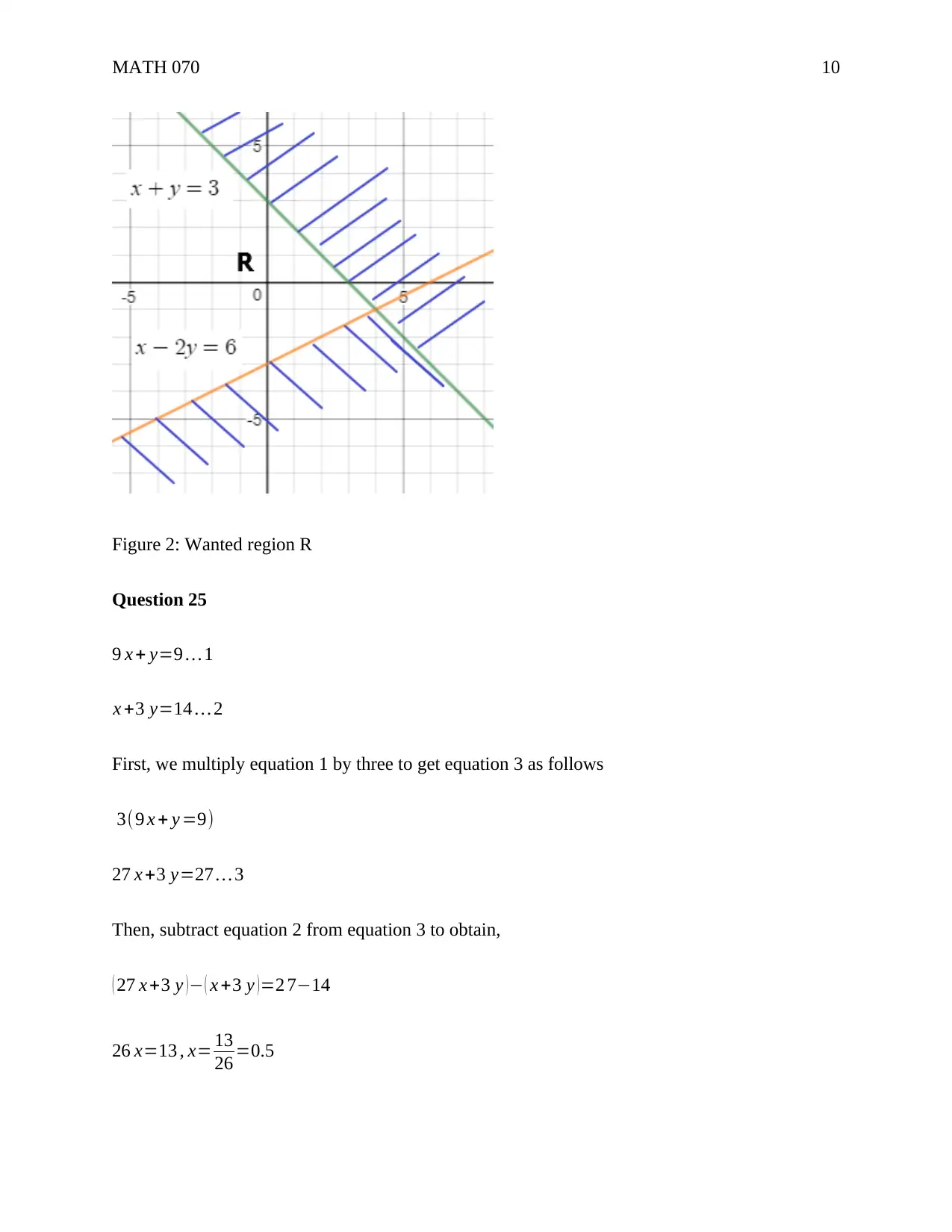
This document presents solutions to a MATH 070 algebra homework assignment, covering a range of topics including solving linear equations, simplifying algebraic expressions, applying the Pythagorean theorem, factoring polynomials, and working with slopes and intercepts. The solutions provide step-by-step explanations for each problem, demonstrating techniques for isolating variables, combining like terms, and manipulating equations to arrive at the correct answers. The assignment includes problems involving graphing linear equations, simplifying rational expressions, evaluating expressions with exponents, and solving systems of equations. The document is available on Desklib, a platform offering a wealth of academic resources including past papers and solved assignments to support student learning.

Running head: MATH 070 1
Math 070
Name
Institution

MATH 070 2
Question 1
2 x−5 y=1 0
Using the equation, we get the coordinates shown in the table below.
x -5 0 5
y -4 -2 0
The resulting graph is shown in figure 1 below:
Figure 1: A graph of 2 x−5 y=1 0
Question 2
3 y +21
5 y −15 . y2− y−6
y2−49
We factorize and simplify the equation as follows:
3 y +21
5 y −15 . y2− y−6
y2−49 = 3 ( y +7)
5( y−3) . y2−3+2 y −6
( y +7)( y−7)
¿ 3( y +7)
5( y−3) . y ( y−3)+2( y −3)
( y+ 7)( y−7)

MATH 070 3
¿ 3( y +7)
5( y−3) . ( y +2)( y −3)
( y +7)( y −7) =3
5
( y +2)
( y−7)
Question 3
v=5 , m=−4
4 v2−m2=4 ( 5 ) 2 − ( −4 ) 2=4 ( 25 ) −16=100−16=84
Question 4
7 ( x−2 )=4 x +1
7 x−14=4 x+1
7 x−4 x=14+1
3 x=15
x= 15
3 =5
Question 5
y2=4 y +12
y2−4 y−12=0
y2−6 y +2 y−12=0
y ( y −6)+ 2( y−6)=0
( y +2 ) ( y−6 ) =0
y +2=0 , y =−2

MATH 070 4
y−6=0 , y=6
Therefore, y=−2∨ y=6
Question 6
Using Pythagoras theorem, c2=102 +242
c2=100+576=676
c= √ 676=26
Question 7
28 w5 n7−35 w n5
7 w n4
First, we simplify the numerator to get,
28 w5 n7−35 w n5
7 w n4 =7 w n5 (4 w4 n2−5)
7 w n4 = 7 w n5
7 w n4 ( 4 w4 n2−5)
¿ n ( 4 w4 n2−5 ) =4 w4 n3−5 n
Question 8
slope of l inethrough ( 2 ,−4 ) ∧(6,7)
slope= y2− y1
x2−x1
=7−(−4 )
6−2 = 7+ 4
4 = 11
4
Question 9
x2−17 x+30
x2−17 x+ 30=x2−15 x−2 x+30

MATH 070 5
¿ x ( x−15 ) −2 ( x−15 ) = ( x−2 ) (x−15)
Question 10
7 x +2 y =11
7 x +2 y −7 x=11−7 x
2 y=1 1−7 x
y= 1 1−7 x
2 =5.5−3.5 x
Question 11
25 x2−49 y2=52 x2−72 y2
Using the rule, a2−b2=(a+ b)(a−b)
52 x2 −72 y2 =(5 x +7 y)(5 x−7 y )
Question 12
4 a+7
a+ 1 − 3 a−10
a+1
The denominator is the same hence, we get
4 a+7
a+1 − 3 a−10
a+1 =1 ( 4 a+7 ) −1 ( 3 a−10 )
a+1 = 4 a+7−3 a+10
a+1
¿ a+17
a+1
Question 13
(5 w ¿¿ 5 y3 )4 =54 (w5 )4 ( y3 )4=54 w20 y12=625 w20 y12 ¿

MATH 070 6
Question 14
( 4 x−7 ) ( 5 x+2 ) =4 x ( 5 x+2 ) −7(5 x +2)
¿ 20 x2+8 x−35 x−14=20 x2−27 x−14
Question 15
8 b2−24 b=8 b(b−3)
Question 16
y-intercept occurs when x=0. So, the line passes through point (0,5)
Let the line pass via another arbitrary point with coordinates (x , y ) so that,
y−5
x−0 =slope=−4
y−5
x =−4
y−5=−4 x
y=−4 x +5
Question 17
(3 y ¿¿ 2−6 y −7)−(8 y2−6 y +1) ¿
(3 y ¿¿ 2−6 y −7)−(8 y2−6 y +1)=(3 y ¿¿ 2−8 y2)−6 y−(−6 y)−7−1 ¿ ¿
¿−5 y2−6 y +6 y−8
¿−5 y2−8

MATH 070 7
Question 18
10 less than twice x is written as 10< 2 x
Question 19
¿ 2 x2 +19 x +2 2
x +5
2 x2 +19 x+22 (2x)
−(2 x2 +10 x)
9 x +22
9 x+22
x +5
9 x +22(9)
− ( 9 x +45 )
−23
Therefore,
2 x2 +19 x+2 2
x +5 =2 x+ 9− 23
x+5
Question 20

MATH 070 8
x−2 y6
x5 y 4 =
y6
( 1
x2 )
x5 y4 = y6
x5 y 4 x2 = y2
x7
Question 21
8+ x
3 =10
8+ x
3 −8=1 0−8
x
3 =2
3 × x
3 =2× 3
x=2 ×3=6
Question 22
(2,1)
Let the line pass via an arbitrary point with coordinates (x , y ) so that the slope becomes,
y−2
x−1 =slope=3
y−2
x−1 × ( x−1 )=3(x −1)
y−2=3 x−3
y−2+ 2=3 x−3+2
y=3 x−1

MATH 070 9
Question 23
y=3 x−11
The equation is in the form, y=m x+ c where m is the gradient and c the y-intercept. By
observation, m=3∧c=−11. Therefore, the slope is 3 whereas the y-intercept is -11.
Question 24
x + y <3
x−2 y <6
x + y=3
x 0 3 5
y 3 0 -2
at point ( 0,0 ) x+ y<3 becomes 0+0<3 , 0<3. The point satisfies the inequality hence we shade the
area above the line.
x−2 y=6
x 0 4 6
y -3 -1 0
at point ( 0,0 ) x−2 y< 6 becomes 0−0<6 , 0< 6. The point satisfies the inequality hence we shade
the area below the line to obtain the wanted region shown in figure 2 below.

MATH 070 10
Figure 2: Wanted region R
Question 25
9 x + y=9 …1
x +3 y=14 … 2
First, we multiply equation 1 by three to get equation 3 as follows
3(9 x + y =9)
27 x +3 y=27 … 3
Then, subtract equation 2 from equation 3 to obtain,
( 27 x +3 y ) − ( x +3 y ) =2 7−14
26 x=13 , x= 13
26 =0.5

MATH 070 11
Substituting x=0.5 into equation 1 we obtain,
9( 0.5)+ y=9
4.5+ y=9
4.5+ y−4.5=9−4.5
y=4.5
Therefore, x=0.5 , y=4.5
Question 26
( 0 ,−5 ) , m=2
3
Let the line pass via an arbitrary point with coordinates (x , y ) so that the slope becomes,
y−−5
x−0 =slope= 2
3
y+ 5
x = 2
3
y+ 5
x × x= 2
3 × x
y +5=2
3 x
y +5−5= 2
3 x−5
y= 2
3 x −5
Question 27

MATH 070 12
( 2 , 3 ) ,m=3
Let the line pass via an arbitrary point with coordinates (x , y ) so that the slope becomes,
y−3
x−2 =slope=3
y−3
x−2 ×(x−2)= 2
3 (x−2)
y−3= 2
3 x− 2
3
y−3+ 3= 2
3 x− 2
3 +3
y= 2
3 x +2 1
3
Question 28
( 0 ,−3 ) , m=0
Let the line pass via an arbitrary point with coordinates (x , y ) so that the slope becomes,
y−−3
x−0 =slope=0
y+ 3
x =0
( y +3)× x=0( x)
y +3=0 ,
y=−3

MATH 070 13
Question 29
( 4 , 3 ) ,m=undefined
When the gradient of a line is undefined, it means that the line is vertical. Therefore, a vertical
line passing through point ( 4 , 3 ) has the equation, x=4
Question 30
( x−2 y ) ( 2 x +3 y )=x ( 2 x +3 y )−2 y (2 x+3 y )
¿ 2 x2 +3 xy−4 xy +6 y2
¿ 2 x2 −xy+ 6 y2
Question 31
3 m2 n−6 mn2+9 mn
3 m2 n−6 mn2+9 mn=3 mn(m−2 n+3)
Question 32
2 w2 +11 w−21
w2−49 ÷(4 w−6)
2 w2 +11 w−21
w2−49 ÷ ( 4 w−6 ) = 2 w2 +11 w−21
w2−49 × 1
( 4 w−6)= 2 w2 +11 w−21
(w ¿¿ 2−49)( 4 w−6)¿
¿ 2 w2+11 w−21
( w¿¿ 2−49)(4 w−6)= 2 w2 +11 w−21
w2 ( 4 w−6 )−49(4 w−6)= 2 w2+11 w−21
4 w3−24 w2−196 w +294 ¿
Question 33

MATH 070 14
6 x
5 . 10
18 x2 = 6 x ( 10 )
5(18 x2) = 60 x
90 x2 = 2
3 x
Question 34
x2
x−4 − 16
x−4 = x2−16
x−4
Using the identity a2−b2= ( a+b ) ( a−b ) , x2−16 becomes
x2−16= ( x+4 ) ( x−4 ) so that ,
x2 −16
x−4 = ( x +4 ) ( x−4 )
x−4 =x +4
Question 35
x
x−4 = 15
x−3 − 2 x
x2−7 x +12
x2−7 x+12=x2−4 x−3 x+12=x ( x−4 ) −3 ( x −4 )= ( x−3 ) ( x−4 ) so that
x
x−4 = 15
x−3 − 2 x
( x−3 ) ( x−4 )
x
x−4 =15 ( x−4 ) −2 x
( x−3 ) ( x−4 ) = 15 x −60−2 x
( x−3 ) ( x−4 ) = 13 x −60
( x−3 ) ( x−4 )
x
x−4 = 13 x−60
( x−3 ) ( x−4 )
x
x−4 ×(x−4)= 13 x−60
( x−3 ) ( x−4 ) ×( x−4)

MATH 070 15
x= 13 x −60
( x−3 )
( x−3 ) x= 13 x −60
( x−3 ) ×(x−3)
x2−3 x=13 x−60
x2−3 x−13 x+ 60=13 x−60−13 x +60=0
x2−16 x+ 60=0
x2−10 x−6 x+ 60=0
x ( x−10)−6 ( x−10)=0
( x−6 ) ( x−10 )=0
x−6=0 , x=6
x−10=0 , x=10
Therefore, x=6∨x=10
Question 36
2
3 x2 y + 3
4 x3 = 2 ( 4 x ) +3(3 y )
12 x3 y = 8 x +9 y
12 x3 y
Question 37
5(2 x2 y )0
Any number raised to power zero equals 1. As a result, (2 x2 y )0=1. Hence,
5(2 x2 y )0=5 ( 1 )=5

MATH 070 16
Question 38
25 x2 y−2
5 x−2 y3 =25
5 x−2−(−2) y−2−3=5 x0 y−5= 5 (1 )
y5 = 5
y5
Question 39
5 x2 y−15 xy +10 x y2=5 xy (x −3+2 y)
Question 40
21 x5−28 x4 +14 x3
7 x = 21 x5
7 x − 28 x4
7 x + 14 x3
7 x =3 x4 −4 x3 +2 x2

MATH 070 17

MATH 070 18