Applied Linear Algebra: Equilibrium Prices and Sector Analysis
VerifiedAdded on 2020/05/04
|4
|412
|309
Homework Assignment
AI Summary
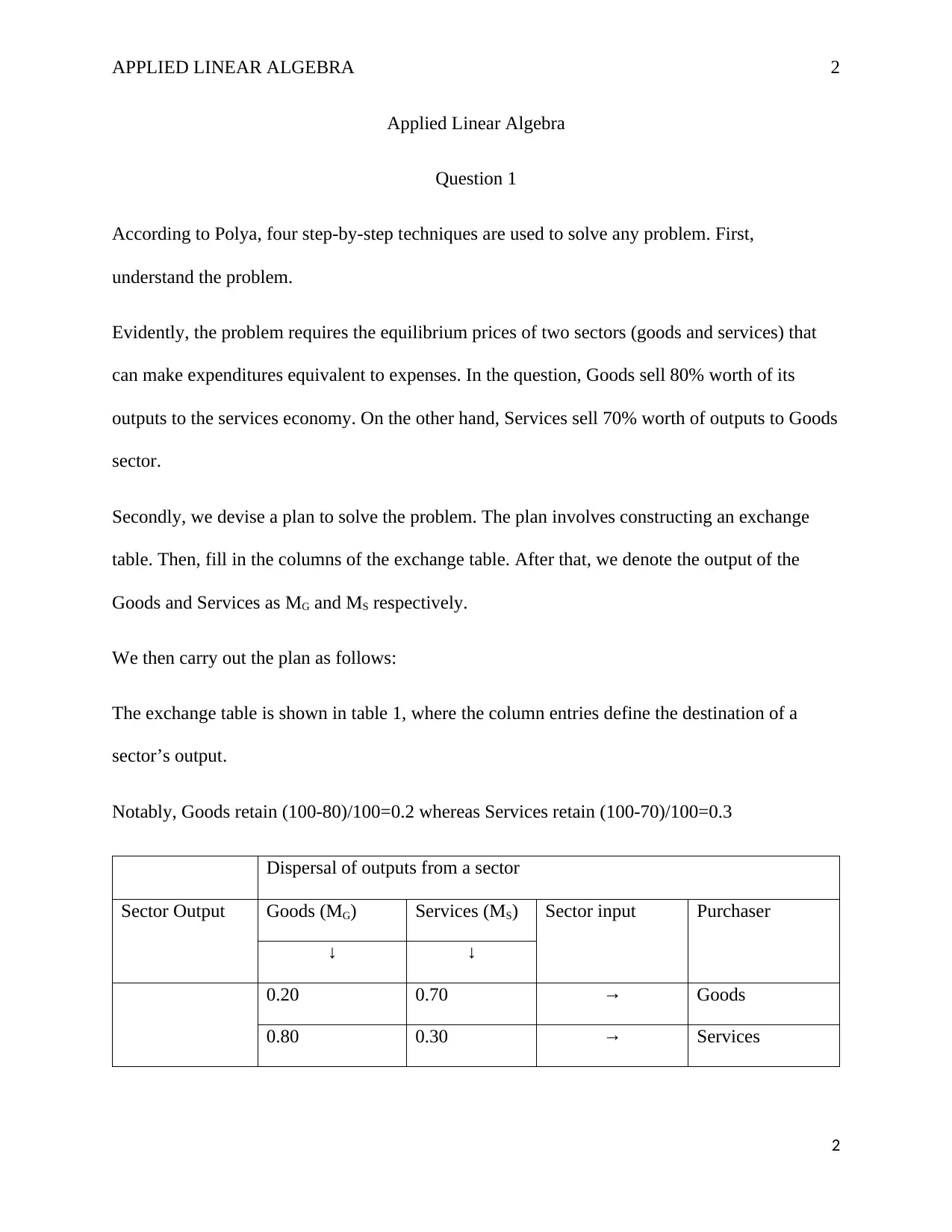
This assignment solution addresses the problem of determining equilibrium prices in a two-sector economy using applied linear algebra. The solution begins by applying Polya's four-step problem-solving method, starting with understanding the problem of determining the equilibrium prices of goods and services. It then constructs an exchange table to represent the flow of goods and services between the two sectors, with Goods selling 80% of its output to Services, and Services selling 70% to Goods. The solution uses the exchange table to calculate the income and expenses for each sector, forming a system of linear equations. The equations are then represented in matrix form and solved, including row reduction of the augmented matrix. The general solution is derived, and the equilibrium prices are determined. The solution emphasizes that only the price ratios matter and that the equilibrium price is unaffected by proportionate price changes. The assignment demonstrates the application of linear algebra principles to economic modeling.
1 out of 4




![[object Object]](/_next/static/media/star-bottom.7253800d.svg)