Math B Assignment

This document is a Math B assignment that discusses various topics related to sine graphs, amplitudes, domains, ranges, and intersections. It also explores the concept of luck as a combination of physical, emotional, and intellectual cycles. The document provides explanations, equations, and graphs to support the discussions.

Math B Assignment
Student’s name: Michael Kong
Teacher’s name: Mr. Gallagher
Draft date: 7/3/2019

Task 1:
Given equation:
Y=AsinBx
Determine A:
A=amplitude is 1.
In the sine graph the amplitude cannot be greater than 1 or less than 1.
Therefore, the amplitude in this graph is 1.
Meaning that A in sin graph equal to 1.
A=1
Determine B
B= 2 π
T when T is period
And T=30
Therefore, B=0.209439510239
Domain
From birth date to first day march (1/3/2019) there are 6,957days
From birth date to last day march (1/3/2019) there are 6,987days
Therefore, the domain of the graph is between 6957 ≤ x ≤ 6987
Range
In this sine graph, the maximum and minimum values are ±1
Therefore, the range is −1 ≤Y ≤ 1
Functions
Because the cycle has a period of 30
y=sin ¿) Domain = 6957 ≤ x ≤ 6987
The graph of y=sin ¿)

Task1(K1,M2)
y= AsinBx
Determine A:
A=amplitude is 1.
In the sine graph, the amplitude cannot be greater than 1 or less than 1.
Hence, the amplitude in this graph is 1.
This means that A in sine graph equal to 1.
A=1
Determine B
T is the period of the cycle
And it given as B= 2 π
T when T is period
But T=23
Therefore B= 0.273181969877
Domain
There are 6569 days since the first day of my birthday to the first day of
March 2019
Also, there are 6599 days since my birthday to the last day of March2019.
Therefore, the domain of the graph is between 6569 ≤ x ≤6599
Range
The range of the graph of sine is −1 ≤Y ≤ 1
Function
Since the physical cycle has a period of 23 days.
Then the function y 1=sin ¿), Domain 6569 ≤ x ≤6599
Therefore, the graph of y=sin ¿)

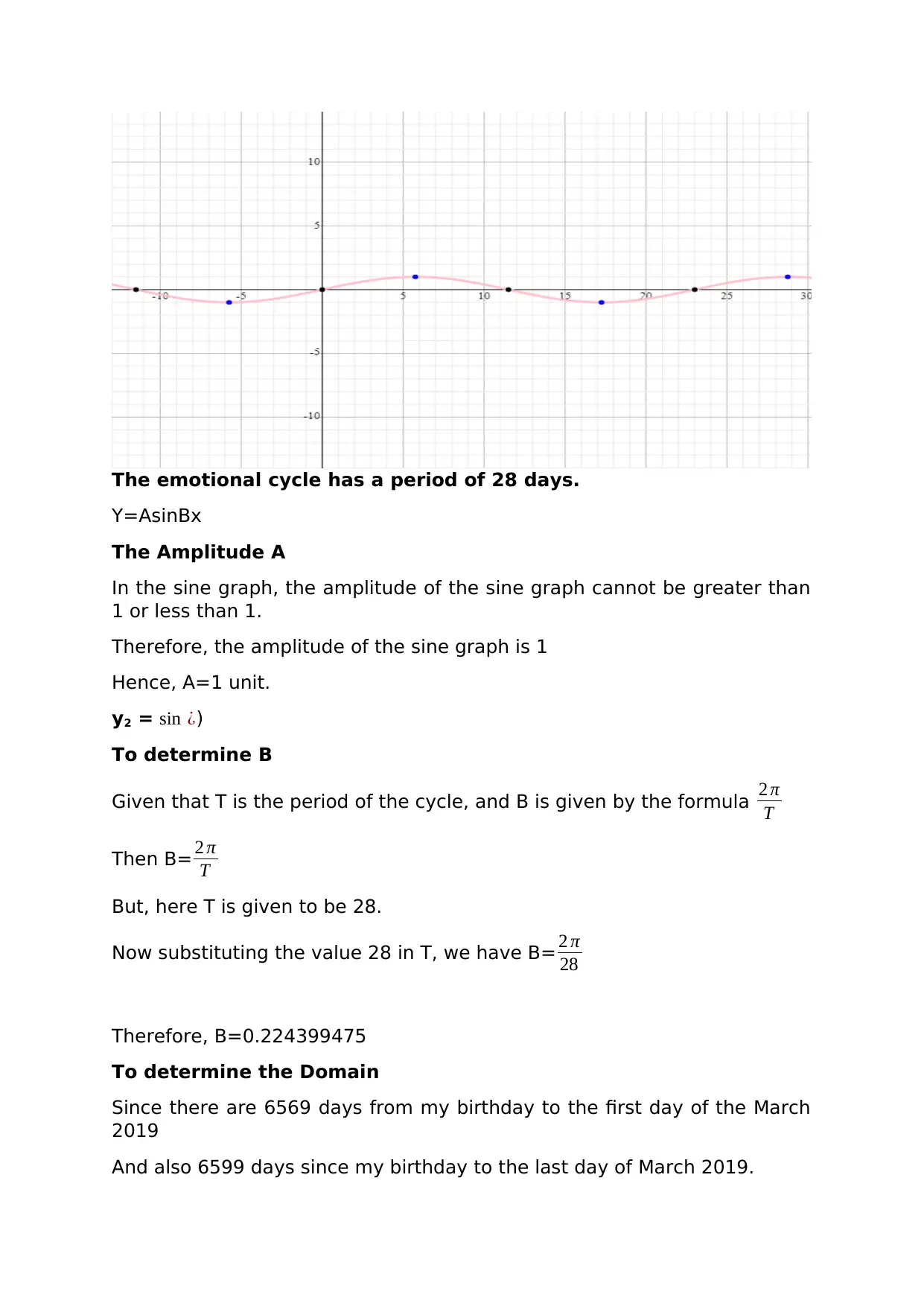
The emotional cycle has a period of 28 days.
Y=AsinBx
The Amplitude A
In the sine graph, the amplitude of the sine graph cannot be greater than
1 or less than 1.
Therefore, the amplitude of the sine graph is 1
Hence, A=1 unit.
y2 = sin ¿)
To determine B
Given that T is the period of the cycle, and B is given by the formula 2 π
T
Then B= 2 π
T
But, here T is given to be 28.
Now substituting the value 28 in T, we have B= 2 π
28
Therefore, B=0.224399475
To determine the Domain
Since there are 6569 days from my birthday to the first day of the March
2019
And also 6599 days since my birthday to the last day of March 2019.

Therefore, the domain of the graph is 6569 ≤ x ≤6599
The Range
The maximum and minimum values of the graph is ±1
The range is −1 ≤ x ≤1 which can be written as −1 ≤ f ( x) ≤ 1
The graph of y2= sin ¿)
The intellectual cycle has a period of 33 days
Y=AsinBx
y3= sin ¿)
The amplitude
The amplitude is 1, since it is the sine graph and all sine graphs cannot
have an amplitude greater than 1 or less than 1.
Meaning A=1
To determine B
T is the period of the intellectual cycle
B= 2 π
T where T is period
And T is given to be 33

Now substituting 33 days in place of T we have B= 2 π
33
B=0.190399554
Domain
From birth date to first day march (1/3/2019) = 6569 days
From birth date to last day march (1/3/2019) = 6602 days
Therefore, the domain of the graph is 6569 ≤ x ≤6602
The Range
The range of the graph is - 1 ≤ x ≤1
Functions
Because the intellectual cycle has a period of 33 days.
y3= sin ¿), domain = 6569 ≤ x ≤6602
Task 2.
y=AsinBx
where A is the amplitude of the sine graph and B= 2 π
T

Give that the three functions are periodic, to calculate how old I was when
the first time any two functions intersect at y=0 and also when the three
functions intersect at y=0.
And Because Sinπ and sin2 π are all equal to 0, the first intersection will be
at sin0=0
Let Equations of the cycles be
P represents y=sin ¿) , Q represents , y=sin ¿) and R represents , y=sin ¿)
Now equating equation P and Q we have
sin ¿)¿ sin ¿) {y=0}
B= 2 π
23
B=0.273181969
Therefore, T= 2 π
B
T=23
Domain
From birth date to first day march is 6569 days
From birth date to last day march is 6599 days
Therefore, the domain of the graph is 6569 ≤ x ≤6599
The Range
The range of the graph is −1 ≤ x ≤1
The function
Because the cycles have a combined period of 23 days and 28 days
sin ¿)¿ sin ¿), Domain=6569 ≤ x ≤6599

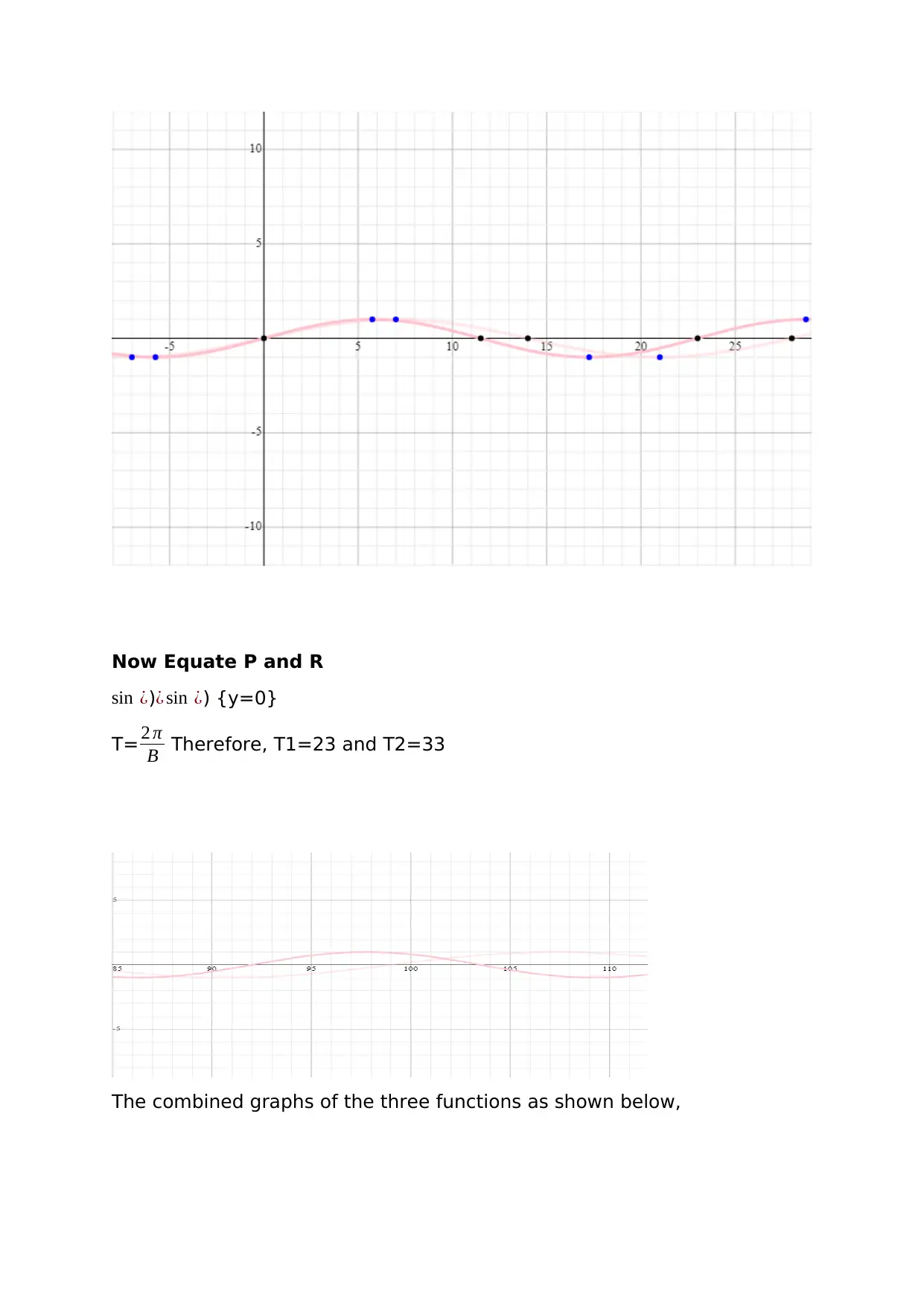
Now Equate P and R
sin ¿)¿ sin ¿) {y=0}
T= 2 π
B Therefore, T1=23 and T2=33
The combined graphs of the three functions as shown below,

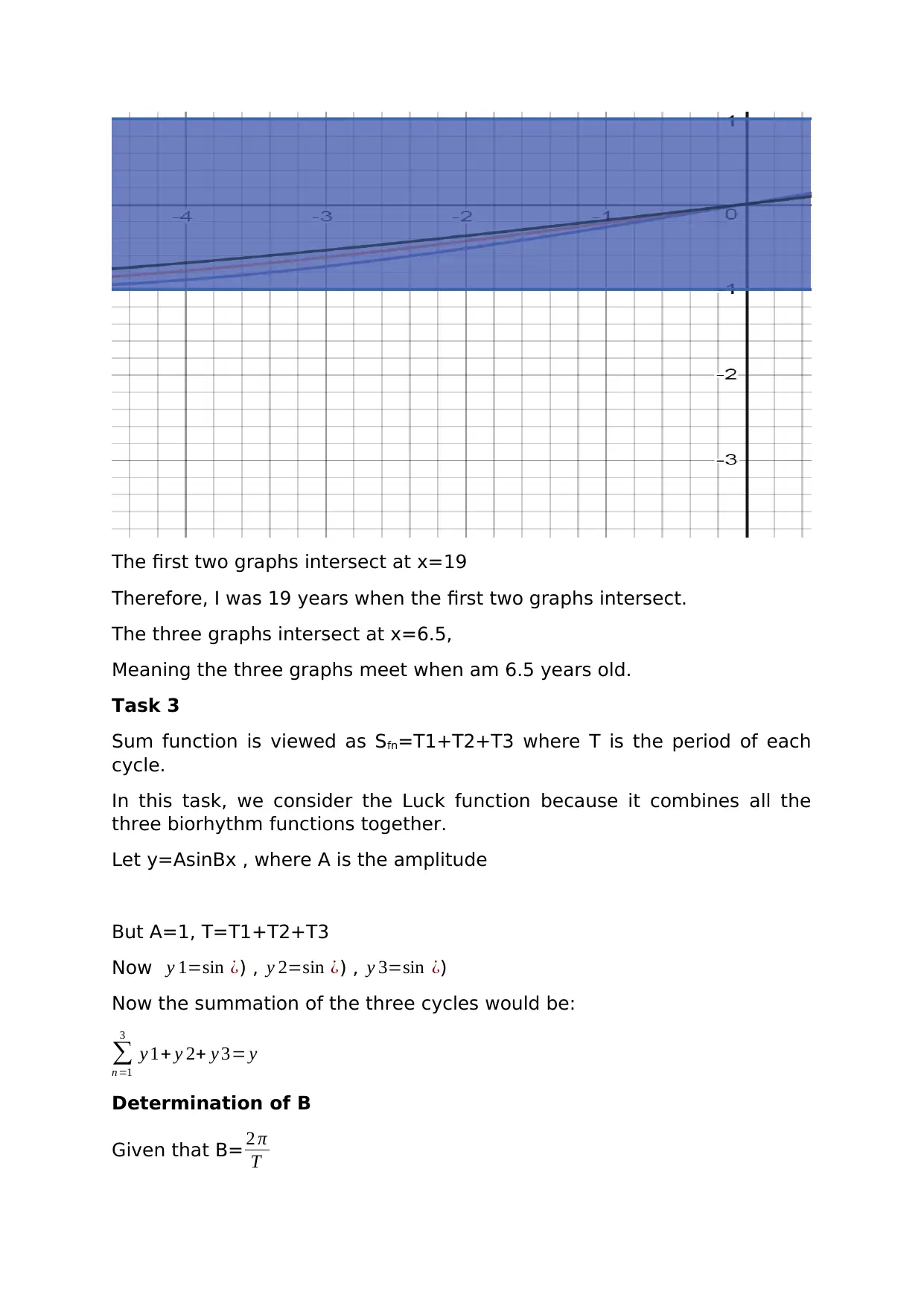
The first two graphs intersect at x=19
Therefore, I was 19 years when the first two graphs intersect.
The three graphs intersect at x=6.5,
Meaning the three graphs meet when am 6.5 years old.
Task 3
Sum function is viewed as Sfn=T1+T2+T3 where T is the period of each
cycle.
In this task, we consider the Luck function because it combines all the
three biorhythm functions together.
Let y=AsinBx , where A is the amplitude
But A=1, T=T1+T2+T3
Now y 1=sin ¿) , y 2=sin ¿) , y 3=sin ¿)
Now the summation of the three cycles would be:
∑
n =1
3
y 1+ y 2+ y 3= y
Determination of B
Given that B= 2 π
T

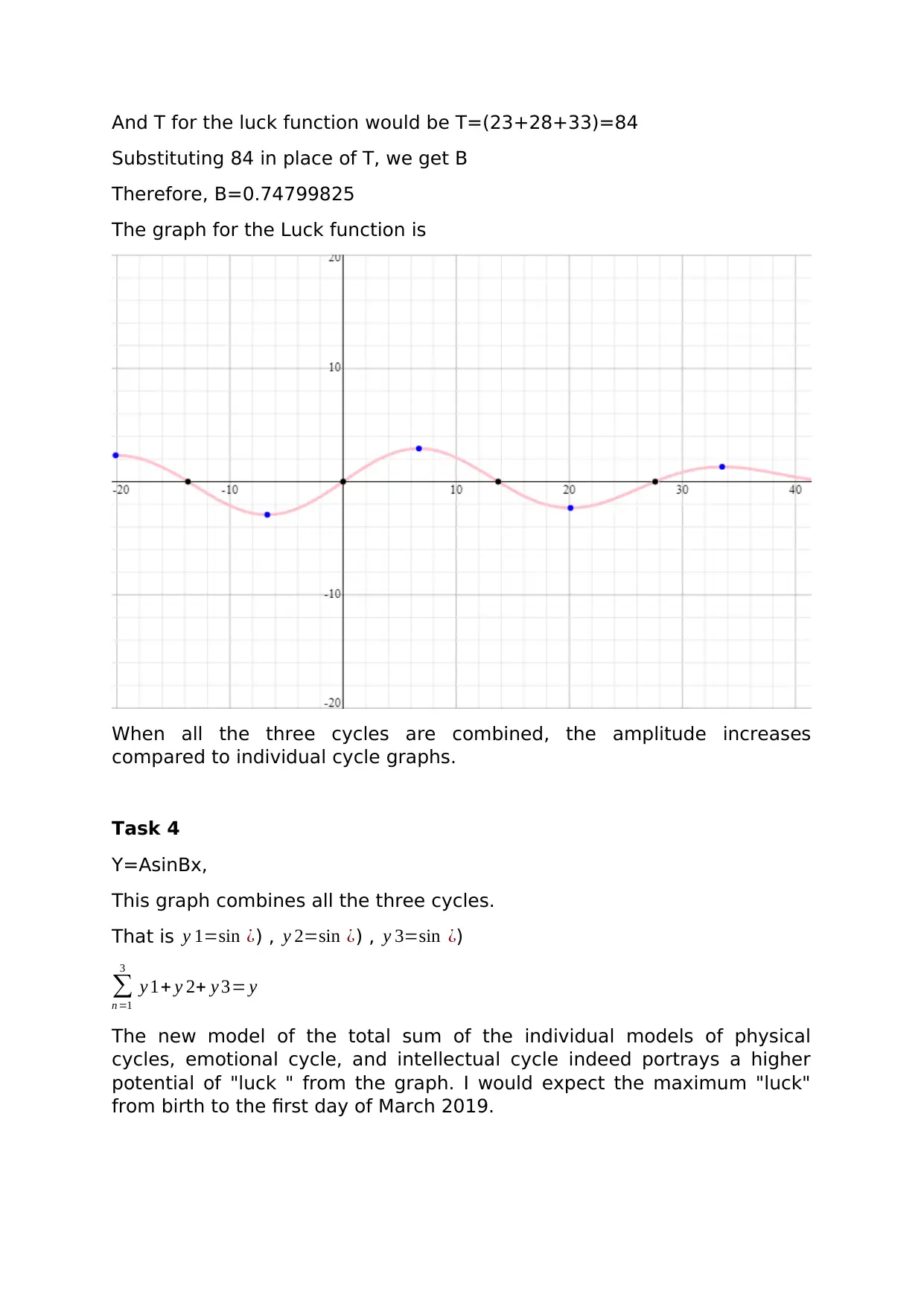
And T for the luck function would be T=(23+28+33)=84
Substituting 84 in place of T, we get B
Therefore, B=0.74799825
The graph for the Luck function is
When all the three cycles are combined, the amplitude increases
compared to individual cycle graphs.
Task 4
Y=AsinBx,
This graph combines all the three cycles.
That is y 1=sin ¿) , y 2=sin ¿) , y 3=sin ¿)
∑
n =1
3
y 1+ y 2+ y 3= y
The new model of the total sum of the individual models of physical
cycles, emotional cycle, and intellectual cycle indeed portrays a higher
potential of "luck " from the graph. I would expect the maximum "luck"
from birth to the first day of March 2019.

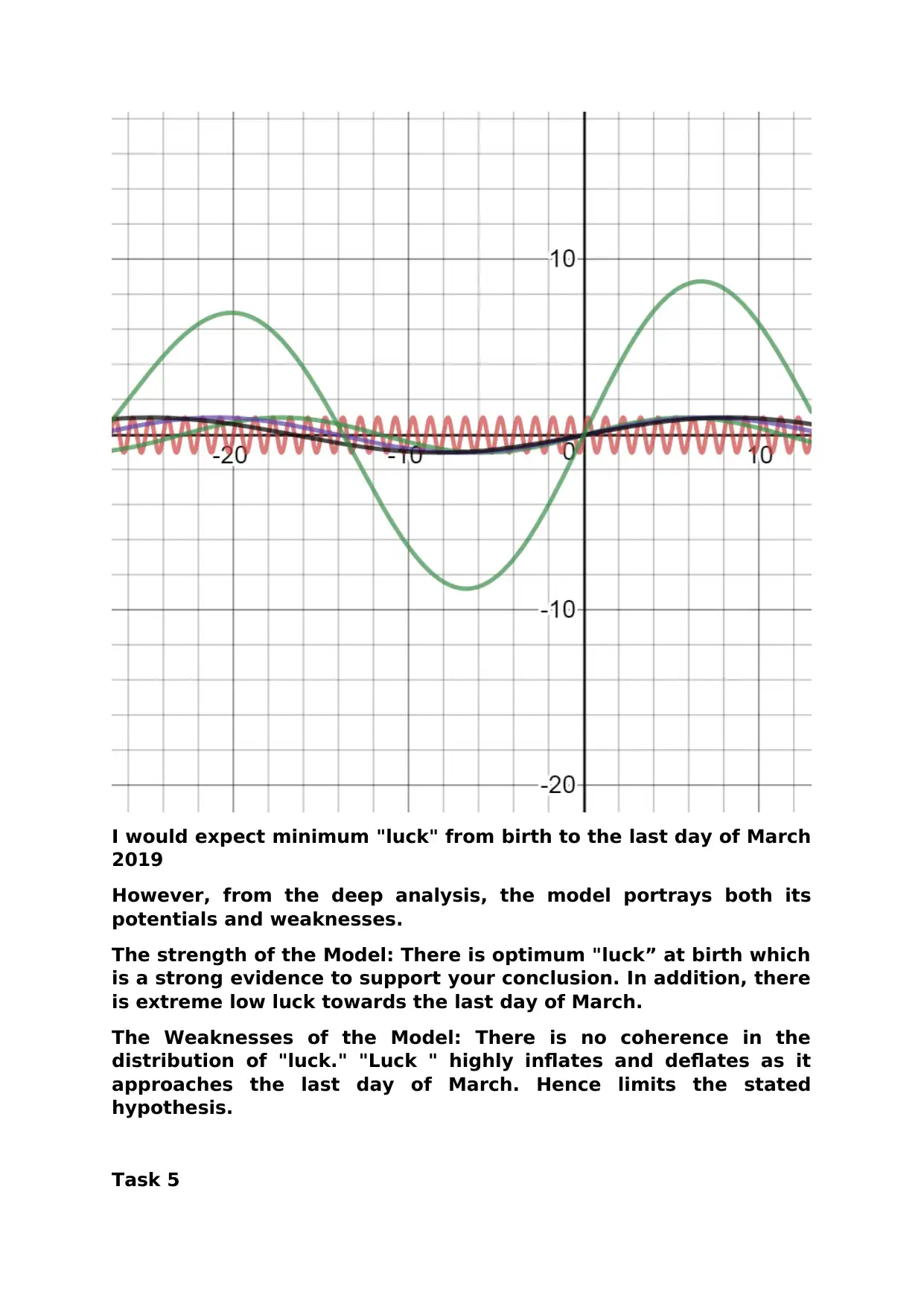
I would expect minimum "luck" from birth to the last day of March
2019
However, from the deep analysis, the model portrays both its
potentials and weaknesses.
The strength of the Model: There is optimum "luck” at birth which
is a strong evidence to support your conclusion. In addition, there
is extreme low luck towards the last day of March.
The Weaknesses of the Model: There is no coherence in the
distribution of "luck." "Luck " highly inflates and deflates as it
approaches the last day of March. Hence limits the stated
hypothesis.
Task 5

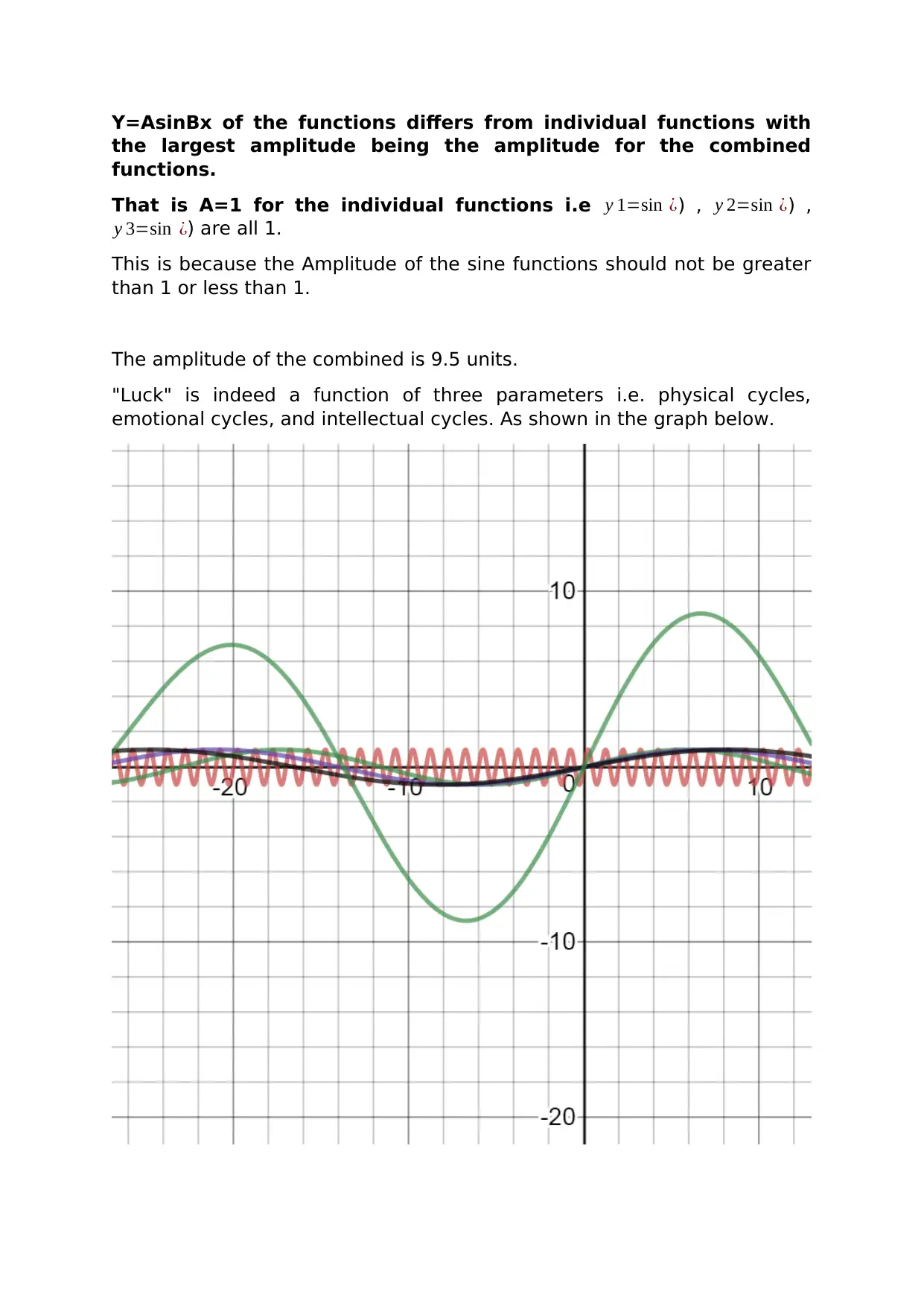
Y=AsinBx of the functions differs from individual functions with
the largest amplitude being the amplitude for the combined
functions.
That is A=1 for the individual functions i.e y 1=sin ¿) , y 2=sin ¿) ,
y 3=sin ¿) are all 1.
This is because the Amplitude of the sine functions should not be greater
than 1 or less than 1.
The amplitude of the combined is 9.5 units.
"Luck" is indeed a function of three parameters i.e. physical cycles,
emotional cycles, and intellectual cycles. As shown in the graph below.

Physical cycle determines the success of physical activities; emotional
cycle, the success of emotional activities and intellectual cycle, the
success of brain activities of which all encompasses the general success.
When the periods are combined, the amplitude increases.
Generally, there is optimum luck expectation at birth, the highest growing
point in life. “Luck" can either appreciate or depreciates from birth
depending on the associated variable factors i.e. individual personality.
When the three functions remain constant from now to the future without
any effect from other variables, there is higher expectation of "luck" in the
future. When the three functions become variables, you might experience
difficulty in predicting the future "luck."