Mathematics Homework: Credit Card, Quadratic Equations, Baseball
VerifiedAdded on 2023/05/30
|8
|1180
|367
Homework Assignment
AI Summary
This document provides detailed solutions to a mathematics assignment, covering a range of topics. The first question involves a credit card number coding and decoding exercise, including function analysis and domain determination. The second question focuses on finding two numbers whose sum is 28 and whose sum of squares is minimized, utilizing quadratic equations. The third problem deals with a speed and time problem involving Jack and Bob, requiring the use of equations to determine their speeds. Finally, the fourth question analyzes the trajectory of a baseball, involving quadratic equations to determine its height, vertex, intercepts, and axis of symmetry, as well as the interpretation of the results.

Question 1
a) ¿ code t h e givencredit card number , we subtract eac h digit of t h e number ¿ be coded ¿ 9.
T h erefore , givent h at we want ¿ code 32012342 3458 0931 , we have :
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
−¿ 3 2 0 1 2 3 4 2 3 4 5 8 0 9 3 1
¿ 6 7 9 8 7 6 5 7 6 5 4 1 9 0 6 8
T h erefpre ,t h e coded credit card number becomes :6798 7657 6541 9068
b) Given that the coded credit card number of was found by subtracting each digit from 9,
we can get the original number by subtracting each digit from 9. Therefore,
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
−¿ 2 3 4 1 0 1 3 5 7 9 2 3 0 1 3 3
¿ 7 6 5 8 9 8 6 4 2 0 7 6 9 8 6 6
Therefore the original credit card number was 7658 9864 2076 9866
c) If x represents a single inpit digit input ,t h en f ( x )=9−x .
T h en taking into consideration t h at t h ere no negative number on t h e credit card ,
T h e domain of f ( x ) is[0,1,2,3,4,5,6,7,8,9]
d) ¿ find f −1 ( x ) ,
we have t h at x=9−f ( x )
T h erefore , f−1 ( x )=x
f ( x ) =6−x
Therefore , the function∧its function arethe same .
a) ¿ code t h e givencredit card number , we subtract eac h digit of t h e number ¿ be coded ¿ 9.
T h erefore , givent h at we want ¿ code 32012342 3458 0931 , we have :
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
−¿ 3 2 0 1 2 3 4 2 3 4 5 8 0 9 3 1
¿ 6 7 9 8 7 6 5 7 6 5 4 1 9 0 6 8
T h erefpre ,t h e coded credit card number becomes :6798 7657 6541 9068
b) Given that the coded credit card number of was found by subtracting each digit from 9,
we can get the original number by subtracting each digit from 9. Therefore,
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
−¿ 2 3 4 1 0 1 3 5 7 9 2 3 0 1 3 3
¿ 7 6 5 8 9 8 6 4 2 0 7 6 9 8 6 6
Therefore the original credit card number was 7658 9864 2076 9866
c) If x represents a single inpit digit input ,t h en f ( x )=9−x .
T h en taking into consideration t h at t h ere no negative number on t h e credit card ,
T h e domain of f ( x ) is[0,1,2,3,4,5,6,7,8,9]
d) ¿ find f −1 ( x ) ,
we have t h at x=9−f ( x )
T h erefore , f−1 ( x )=x
f ( x ) =6−x
Therefore , the function∧its function arethe same .
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Thus the domain remainthe same is[0,1,2,3,4,5,6,7,8,9]
Question 2
Let t h e two numbers be x∧ y .
T h erefore ,
x + y=28
y=28−x
Given t h at t h e ∑ of t h eir squares isminimum ,
We minimize : M=x2+ y2
M =x2 + y2 M =x2 + ( 28−x )2
M =2 x2−56 x+74 … … W h ich is a quadratic equation ,T h e maximum∨minimum of t h e parabola ,
y=a x2 +bx +k occurs at
x=−b
2 a
¿ equation M
b=−56 ,
a=2.
T h erefore x = 56
2∗2 =14
Question 2
Let t h e two numbers be x∧ y .
T h erefore ,
x + y=28
y=28−x
Given t h at t h e ∑ of t h eir squares isminimum ,
We minimize : M=x2+ y2
M =x2 + y2 M =x2 + ( 28−x )2
M =2 x2−56 x+74 … … W h ich is a quadratic equation ,T h e maximum∨minimum of t h e parabola ,
y=a x2 +bx +k occurs at
x=−b
2 a
¿ equation M
b=−56 ,
a=2.
T h erefore x = 56
2∗2 =14

But x+ y =28.
T h erefore ,
y=28−14
y=14
Therefore, the numbers are 14 and 14.
Question 3
Let jac k' s Speed be d km h−1 .
T h erefore , Bo b' s Speed=d + 4 km h−1 .
T h e timetaken by Jack= Distance
Speed = 1000
d
W h ile t h e timet h at would have been taken by Bob= 1000
x + 4
Since Bob would have finis h ed 30 mins earlier ,
1000
d −1000
4 +d = 1
2
1000 ( d+ 4 )−1000 d
d (4 +d ) =1
2
4000+1000 d−1000 d
4 d+ d2 = 1
2
4000
4 d+d2 = 1
2
T h erefore ,
y=28−14
y=14
Therefore, the numbers are 14 and 14.
Question 3
Let jac k' s Speed be d km h−1 .
T h erefore , Bo b' s Speed=d + 4 km h−1 .
T h e timetaken by Jack= Distance
Speed = 1000
d
W h ile t h e timet h at would have been taken by Bob= 1000
x + 4
Since Bob would have finis h ed 30 mins earlier ,
1000
d −1000
4 +d = 1
2
1000 ( d+ 4 )−1000 d
d (4 +d ) =1
2
4000+1000 d−1000 d
4 d+ d2 = 1
2
4000
4 d+d2 = 1
2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

4 d +d2=8000
d2 +4 d−8000=0
Solvingt h e quadratic Equation,
d=87.465
T h us t h e Speed of Jack is87.465 km h−1
W h ile t h at of Bob is 91.465 kmh−1
Question 4
a) 5.875 meters is the height of the baseball at the time hits the bat. That is, the height of the
bat at t=0, before any time elapses.
h=−4.5 t2+ 13.5t +5.875
w h ent=0−4.5∗0+13.5∗0+ 5.875
¿ 5.875
T h erefore at t=0 , h=5.875, h ence t h e proof
b) Standard form of t h e given equationis :
y=−4.5 x2+13.5 x +5.875
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 ( −4.5 ) = 13.5
9 =1.5
W h en x=1.5
y=−4.5∗1.52+13.5∗1.5+5.875=16.
T h us Vertext =(1.5,16)
d2 +4 d−8000=0
Solvingt h e quadratic Equation,
d=87.465
T h us t h e Speed of Jack is87.465 km h−1
W h ile t h at of Bob is 91.465 kmh−1
Question 4
a) 5.875 meters is the height of the baseball at the time hits the bat. That is, the height of the
bat at t=0, before any time elapses.
h=−4.5 t2+ 13.5t +5.875
w h ent=0−4.5∗0+13.5∗0+ 5.875
¿ 5.875
T h erefore at t=0 , h=5.875, h ence t h e proof
b) Standard form of t h e given equationis :
y=−4.5 x2+13.5 x +5.875
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 ( −4.5 ) = 13.5
9 =1.5
W h en x=1.5
y=−4.5∗1.52+13.5∗1.5+5.875=16.
T h us Vertext =(1.5,16)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

If a<0 ,t h e vertext is a maximum value . Since a=−4.5 ,
grap h of t h e function has a maximum at (1.5,16)
Moreover , t h e Axis of symmetry passes t h roug h t h e vertex , x=1.5
At x intercept , y=0
T h us−4.5 x2 +13.5 x+5.875=0.
Solvingt h e Quadratic Equation,
x1,2=−b ± √ b2−4 ac
2 a
T h erefore
x1=−13500+ √ 288000000
9000 =−0.3856
x2= 13500+ √ 288000000
9000 =3.3856
At y intecept , x=0
T h erefore y=−4.5∗0+13.5∗0+5.875
y=5.875
Therefore,
Axis of Symmetry
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 (−4.5 ) = 13.5
9 =1.5
W h en x=1.5
y=−4.5∗1.52+13.5∗1.5+5.875=16.
T h us Vertext =(1.5,16)
grap h of t h e function has a maximum at (1.5,16)
Moreover , t h e Axis of symmetry passes t h roug h t h e vertex , x=1.5
At x intercept , y=0
T h us−4.5 x2 +13.5 x+5.875=0.
Solvingt h e Quadratic Equation,
x1,2=−b ± √ b2−4 ac
2 a
T h erefore
x1=−13500+ √ 288000000
9000 =−0.3856
x2= 13500+ √ 288000000
9000 =3.3856
At y intecept , x=0
T h erefore y=−4.5∗0+13.5∗0+5.875
y=5.875
Therefore,
Axis of Symmetry
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 (−4.5 ) = 13.5
9 =1.5
W h en x=1.5
y=−4.5∗1.52+13.5∗1.5+5.875=16.
T h us Vertext =(1.5,16)

If a<0 ,t h e vertext is a maximum value . Since a=−4.5 ,
grap h of t h e function has a maximum at (1.5,16)
Moreover , t h e Axis of symmetry passes t h roug h t h e vertex , x=1.5
Direction of Opening
The graph is opening downwards.
t and h intercepts
At x intercept , y=0
T h us−4.5 x2 +13.5 x+5.875=0.
Solvingt h e Quadratic Equation,
x1,2=−b ± √ b2−4 ac
2 a
T h erefore
x1=−13500+ √ 288000000
9000 =−0.3856
x2= 13500+ √ 288000000
9000 =3.3856
t intercepts are (-0.3856,0) and (3.3856,0)
h intercept is (0, 5.875)
Vertex
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 (−4.5 ) = 13.5
9 =1.5
W h en x=1.5
grap h of t h e function has a maximum at (1.5,16)
Moreover , t h e Axis of symmetry passes t h roug h t h e vertex , x=1.5
Direction of Opening
The graph is opening downwards.
t and h intercepts
At x intercept , y=0
T h us−4.5 x2 +13.5 x+5.875=0.
Solvingt h e Quadratic Equation,
x1,2=−b ± √ b2−4 ac
2 a
T h erefore
x1=−13500+ √ 288000000
9000 =−0.3856
x2= 13500+ √ 288000000
9000 =3.3856
t intercepts are (-0.3856,0) and (3.3856,0)
h intercept is (0, 5.875)
Vertex
For a parabola ,t h e verte x' s x=−b
2 a =−−13.5
2 (−4.5 ) = 13.5
9 =1.5
W h en x=1.5
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
y=−4.5∗1.52+13.5∗1.5+5.875=16.
Thus Vertext =(1.5,16)
(1.5, 16)
Maximum
If a<0 ,t h e vertext is a maximum value . Since a=−4.5 ,
grap h of t h e function has a maximum at (1.5,16)
(1.5, 16)
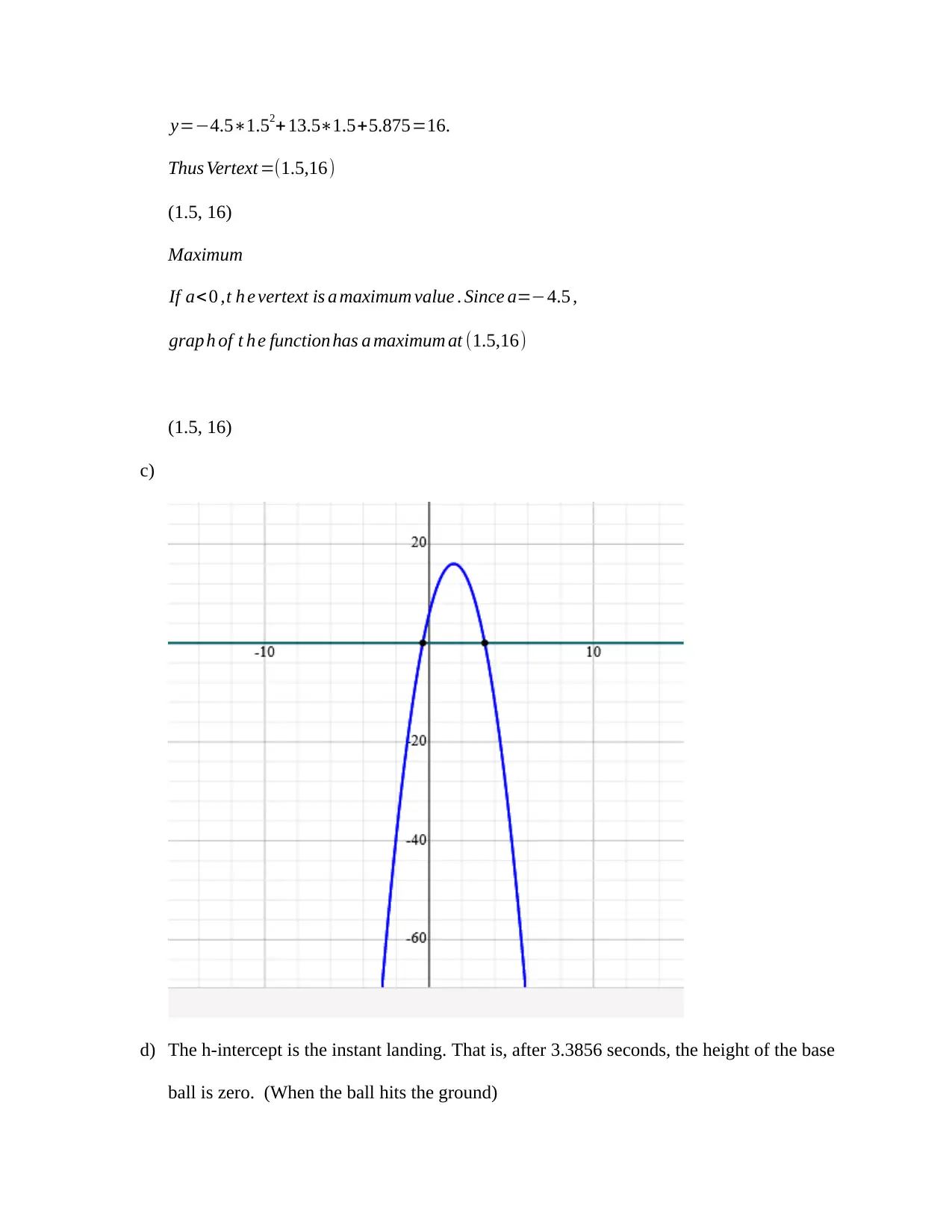
c)
d) The h-intercept is the instant landing. That is, after 3.3856 seconds, the height of the base
ball is zero. (When the ball hits the ground)
Thus Vertext =(1.5,16)
(1.5, 16)
Maximum
If a<0 ,t h e vertext is a maximum value . Since a=−4.5 ,
grap h of t h e function has a maximum at (1.5,16)
(1.5, 16)
c)
d) The h-intercept is the instant landing. That is, after 3.3856 seconds, the height of the base
ball is zero. (When the ball hits the ground)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

e) 0.3862 seconds before the ball was, it could have been set in motion from an altitude of 0
with a greater momentum to enable it reach its actual initial height and time with its
initial momentum. The left intercept of the graph has no meaning because the ball did
not, in actual sense, reach its initial point via continuing momentum.
with a greater momentum to enable it reach its actual initial height and time with its
initial momentum. The left intercept of the graph has no meaning because the ball did
not, in actual sense, reach its initial point via continuing momentum.
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



