Electrical Engineering: Mathematical Models and Statistical Techniques
VerifiedAdded on 2023/01/09
|12
|1347
|23
Homework Assignment
AI Summary
This document presents a comprehensive solution to an electrical engineering assignment focusing on mathematical models and statistical techniques. The solution covers various aspects, including dimensional analysis to predict physical relationships, calculations involving arithmetic and geometric series, and analysis of capacitor voltage behavior. Furthermore, the assignment delves into statistical analysis, calculating mean, variance, and standard deviation from sample data. It also addresses probability calculations related to metal bolts exceeding tolerance values and explores the relationship between fuel consumption and fuel economy. The document provides detailed step-by-step solutions and explanations for each problem, making it a valuable resource for students studying electrical engineering.

Mathematical Models and
Statistical Techniques
Statistical Techniques
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Table of Contents
PART 1............................................................................................................................................1
PART 2............................................................................................................................................7
PART 1............................................................................................................................................1
PART 2............................................................................................................................................7

PART 1
(a) Given,
P = V2/R
here, unit of power P is watt (joules per sec)
unit of voltage V is volts and,
unit of resistance is ohm
in dimensional form,
P = m2.kg.sec-3
= L2 M1T-3
and,
V = m2.kg.sec-3 .A-1
= L2 M1T-3
then,
R = V2/P
= (L2 M1T-3 .A-1)2
(L2 M1T-3)
= L2 M1T-3 A-2
= m2.kg.sec-3 A-2
(b) t = 2π √m3l
F
here, m is mass,
l is length and,
F is tension
in dimensional form,
F = m x g
= m.kg.sec-2
= L1 M1T-2
then,
1
(a) Given,
P = V2/R
here, unit of power P is watt (joules per sec)
unit of voltage V is volts and,
unit of resistance is ohm
in dimensional form,
P = m2.kg.sec-3
= L2 M1T-3
and,
V = m2.kg.sec-3 .A-1
= L2 M1T-3
then,
R = V2/P
= (L2 M1T-3 .A-1)2
(L2 M1T-3)
= L2 M1T-3 A-2
= m2.kg.sec-3 A-2
(b) t = 2π √m3l
F
here, m is mass,
l is length and,
F is tension
in dimensional form,
F = m x g
= m.kg.sec-2
= L1 M1T-2
then,
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

dimension of t as per given formula –
t = √M3L1
L1 M1T-2
= √M2T2
= MT = kg sec
which is mathematically wrong, therefore, given formula of period of vibration (t) is incorrect.
(c) Given, samples of voltage = 2, 4, 6, … 40
using arithmetic series formula –
Sn = n [a + l]
2
here, n is no. of terms
a is first term
l is last term
in given sample,
a = 2, n = 20 and l = 40
Sum of 20 voltage samples =
Sn = n [a + l]
2
Sn = 20 [2 + 40]
2
= 10 x 42 = 420 mV
(d) Given, sequence = 1024, 2048, 4096, 8192 …
using geometric series formula –
Tn = a. rn-1
here, n is no. of terms
a is first term
r is ratio of succeeding and preceding term (II/I)
in given series,
a = 1024 and r = 2048/1024 = 2
2
t = √M3L1
L1 M1T-2
= √M2T2
= MT = kg sec
which is mathematically wrong, therefore, given formula of period of vibration (t) is incorrect.
(c) Given, samples of voltage = 2, 4, 6, … 40
using arithmetic series formula –
Sn = n [a + l]
2
here, n is no. of terms
a is first term
l is last term
in given sample,
a = 2, n = 20 and l = 40
Sum of 20 voltage samples =
Sn = n [a + l]
2
Sn = 20 [2 + 40]
2
= 10 x 42 = 420 mV
(d) Given, sequence = 1024, 2048, 4096, 8192 …
using geometric series formula –
Tn = a. rn-1
here, n is no. of terms
a is first term
r is ratio of succeeding and preceding term (II/I)
in given series,
a = 1024 and r = 2048/1024 = 2
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

9th count of the chip will be calculated by geometric formula as –
Tn = a. rn-1
= 1024 (2)9 – 1
= 1024. 28
=1024 x 256
= 262,144
(e) Given,
Voltage across the capacitor (Vc)
Vc = Vs (1 − e −𝑡 /𝑅𝐶)
here,
Vs = 12V
R = 1MΏ = 1 x 1012 μΏ
t = 4sec and Vc = 2V
Then, value of capacitor can be calculated by using –
Vc = (1 − e −𝑡 /𝑅𝐶)
Vs
e −𝑡 /𝑅𝐶 = 1 -Vc
Vs
exp (-4/1012x C) = 1 – 2/12
exp (-4 x 10-12/C) = 5/6
exp (-4x10-12) exp(1/C) = 5/6
1.000000000004 e1/C = 0.84
e1/C = 0.84
1/C = log (0.84)
C ≈ 13V
3
Tn = a. rn-1
= 1024 (2)9 – 1
= 1024. 28
=1024 x 256
= 262,144
(e) Given,
Voltage across the capacitor (Vc)
Vc = Vs (1 − e −𝑡 /𝑅𝐶)
here,
Vs = 12V
R = 1MΏ = 1 x 1012 μΏ
t = 4sec and Vc = 2V
Then, value of capacitor can be calculated by using –
Vc = (1 − e −𝑡 /𝑅𝐶)
Vs
e −𝑡 /𝑅𝐶 = 1 -Vc
Vs
exp (-4/1012x C) = 1 – 2/12
exp (-4 x 10-12/C) = 5/6
exp (-4x10-12) exp(1/C) = 5/6
1.000000000004 e1/C = 0.84
e1/C = 0.84
1/C = log (0.84)
C ≈ 13V
3

(g) y = 60 cosh (x/60)
when x = 104 then, y will be
y = 60 cosh (104/60)
= 60 x 0.364
= 21.84
when y = 180 then, x will be
180 = 60 cosh (x/60)
cosh(x/60) = 3
x/60 = cosh-1(3)
x = 60 x 0.327 = 19.62
(h) Dimensional analysis to predict t
Let, in a simple pendulum
t ∝ m
or, t ∝ l
or, t ∝ g
Then,
t = k × ma lb gc
where, k is a proportionality constant then,
here, g = m/sec2
which is dimensionally can be written as
g = LT-2
and m is mass then dimensionally – M
and l is length = L
then,
given formula of t =
T = Ma Lb (LT-2)c
= Ma Lb Lc T-2c
= Ma. Lb+c T-2c
For consistency,
from M: a = 0
T: -2c = 1 or, c = - ½
4
when x = 104 then, y will be
y = 60 cosh (104/60)
= 60 x 0.364
= 21.84
when y = 180 then, x will be
180 = 60 cosh (x/60)
cosh(x/60) = 3
x/60 = cosh-1(3)
x = 60 x 0.327 = 19.62
(h) Dimensional analysis to predict t
Let, in a simple pendulum
t ∝ m
or, t ∝ l
or, t ∝ g
Then,
t = k × ma lb gc
where, k is a proportionality constant then,
here, g = m/sec2
which is dimensionally can be written as
g = LT-2
and m is mass then dimensionally – M
and l is length = L
then,
given formula of t =
T = Ma Lb (LT-2)c
= Ma Lb Lc T-2c
= Ma. Lb+c T-2c
For consistency,
from M: a = 0
T: -2c = 1 or, c = - ½
4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

L: b + c = 0 or, b = ½
then, put these value in given equation, formula for t will be arrived as –
t = k × m0 l1/2 g-1/2
t = k √l/g
or, t ∝ √l/g
(i) Dimensional analysis to predict speed of sound (u) –
let assume
u ∝ pa rb gc
or, u = k. pa rb gc (k is proportionality constant)
here, p is pressure
r is gas density
and, g is gravity
dimensionally can be written as
p = N/m2
= m-1 .kg. s-2
= M1 L-1 T-2
while,
r = kg/m3
= M1 L-3 T0
and, g = m/sec2
g = LT-2
and, speed = m/sec = M0 L1 T-1
then,
given formula of speed =
u = k. pa rb gc
(M0 L1 T-1) = (M1 L-1 T-2)a (M1 L-3 T0)b (LT-2)c
= Ma+b. L-a-3b+c T-2(a+c)
For consistency,
a = ½ , b = -½ and c = 0
then, put these value in given equation, formula for t will be arrived as –
5
then, put these value in given equation, formula for t will be arrived as –
t = k × m0 l1/2 g-1/2
t = k √l/g
or, t ∝ √l/g
(i) Dimensional analysis to predict speed of sound (u) –
let assume
u ∝ pa rb gc
or, u = k. pa rb gc (k is proportionality constant)
here, p is pressure
r is gas density
and, g is gravity
dimensionally can be written as
p = N/m2
= m-1 .kg. s-2
= M1 L-1 T-2
while,
r = kg/m3
= M1 L-3 T0
and, g = m/sec2
g = LT-2
and, speed = m/sec = M0 L1 T-1
then,
given formula of speed =
u = k. pa rb gc
(M0 L1 T-1) = (M1 L-1 T-2)a (M1 L-3 T0)b (LT-2)c
= Ma+b. L-a-3b+c T-2(a+c)
For consistency,
a = ½ , b = -½ and c = 0
then, put these value in given equation, formula for t will be arrived as –
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

u = k × p1/2 r-1/2 g0
u = k √p/r
or, u ∝ √p/r
6
u = k √p/r
or, u ∝ √p/r
6
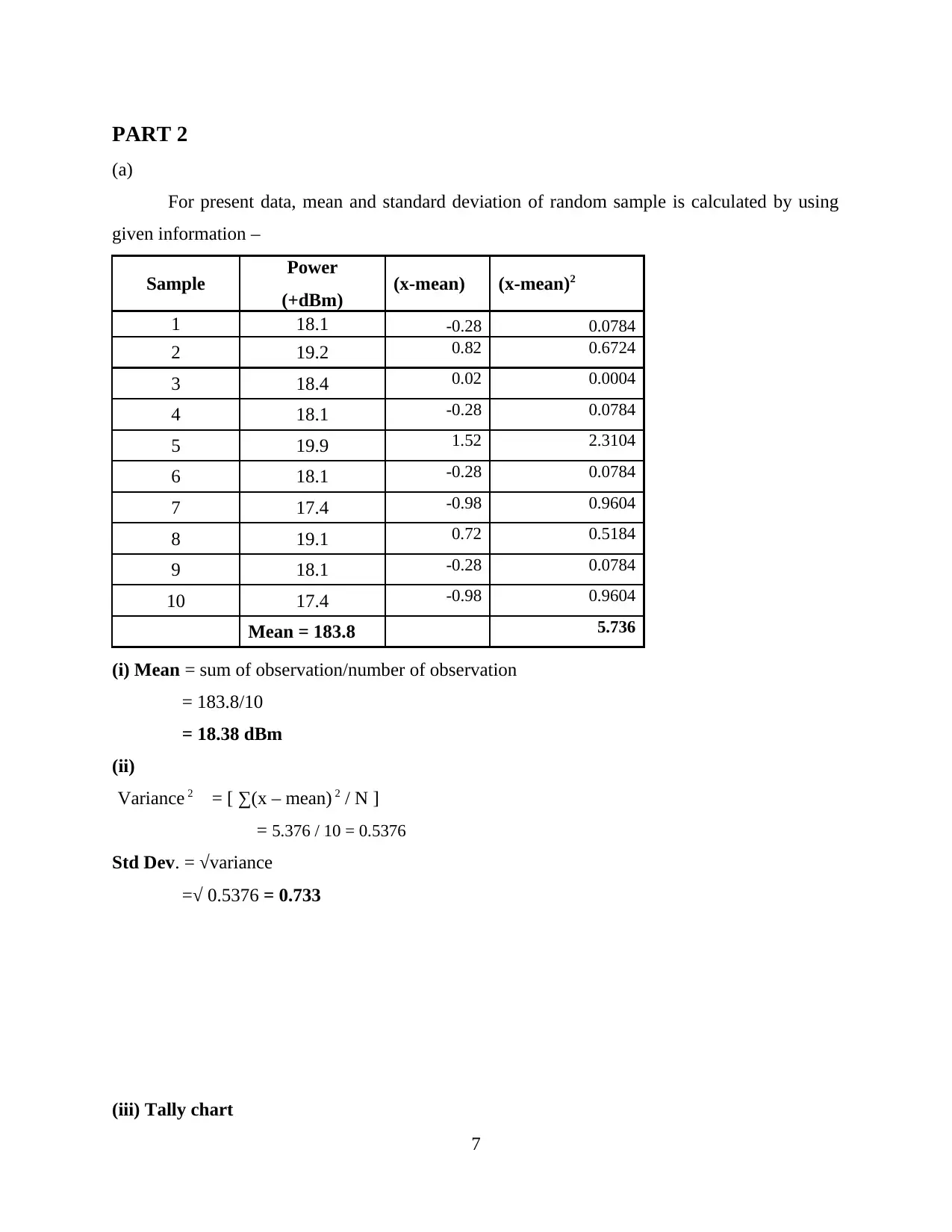
PART 2
(a)
For present data, mean and standard deviation of random sample is calculated by using
given information –
Sample Power
(+dBm) (x-mean) (x-mean)2
1 18.1 -0.28 0.0784
2 19.2 0.82 0.6724
3 18.4 0.02 0.0004
4 18.1 -0.28 0.0784
5 19.9 1.52 2.3104
6 18.1 -0.28 0.0784
7 17.4 -0.98 0.9604
8 19.1 0.72 0.5184
9 18.1 -0.28 0.0784
10 17.4 -0.98 0.9604
Mean = 183.8 5.736
(i) Mean = sum of observation/number of observation
= 183.8/10
= 18.38 dBm
(ii)
Variance 2 = [ ∑(x – mean) 2 / N ]
= 5.376 / 10 = 0.5376
Std Dev. = √variance
=√ 0.5376 = 0.733
(iii) Tally chart
7
(a)
For present data, mean and standard deviation of random sample is calculated by using
given information –
Sample Power
(+dBm) (x-mean) (x-mean)2
1 18.1 -0.28 0.0784
2 19.2 0.82 0.6724
3 18.4 0.02 0.0004
4 18.1 -0.28 0.0784
5 19.9 1.52 2.3104
6 18.1 -0.28 0.0784
7 17.4 -0.98 0.9604
8 19.1 0.72 0.5184
9 18.1 -0.28 0.0784
10 17.4 -0.98 0.9604
Mean = 183.8 5.736
(i) Mean = sum of observation/number of observation
= 183.8/10
= 18.38 dBm
(ii)
Variance 2 = [ ∑(x – mean) 2 / N ]
= 5.376 / 10 = 0.5376
Std Dev. = √variance
=√ 0.5376 = 0.733
(iii) Tally chart
7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Sample Tally Frequency
17.4 / / 2
18.1 / / / / 4
18.4 / 1
19.1 / 1
19.2 / 1
19.9 / 1
Total 10
(b)
Metal bolts in tolerance value = 94%
q = 94 = 0.94
100
and, number of metal bolts exceed tolerance value (p) = 6/100 =0.06
Now, probability two of six withdrawn bolts exceed the tolerance value –
p (2) = n(n – 1) q (n – 2) .p (2)
2
= 6 (6 – 1) 0.94 (6 – 2). 0.6 (2)
2
(i) Probability of Two of the six bolts exceed the diameter –
P(2) = 0.0396
(ii) More than two of the six bolts exceed the diameter –
p(>2) = 1 – {p(0) + p(1) + p(2)}
= 1 – {0.94 + 6 x 0.94 x 0.06 + 0.0396}
= 1 – 1.318 = 0.318
(c) Given,
8
17.4 / / 2
18.1 / / / / 4
18.4 / 1
19.1 / 1
19.2 / 1
19.9 / 1
Total 10
(b)
Metal bolts in tolerance value = 94%
q = 94 = 0.94
100
and, number of metal bolts exceed tolerance value (p) = 6/100 =0.06
Now, probability two of six withdrawn bolts exceed the tolerance value –
p (2) = n(n – 1) q (n – 2) .p (2)
2
= 6 (6 – 1) 0.94 (6 – 2). 0.6 (2)
2
(i) Probability of Two of the six bolts exceed the diameter –
P(2) = 0.0396
(ii) More than two of the six bolts exceed the diameter –
p(>2) = 1 – {p(0) + p(1) + p(2)}
= 1 – {0.94 + 6 x 0.94 x 0.06 + 0.0396}
= 1 – 1.318 = 0.318
(c) Given,
8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Mean capacitance of 400 capacitors = 100μF
Standard deviation = 7μF
Given, that capacitance are normally distributed then,
__
Z = X – μ
σ
= 100 – μ
7
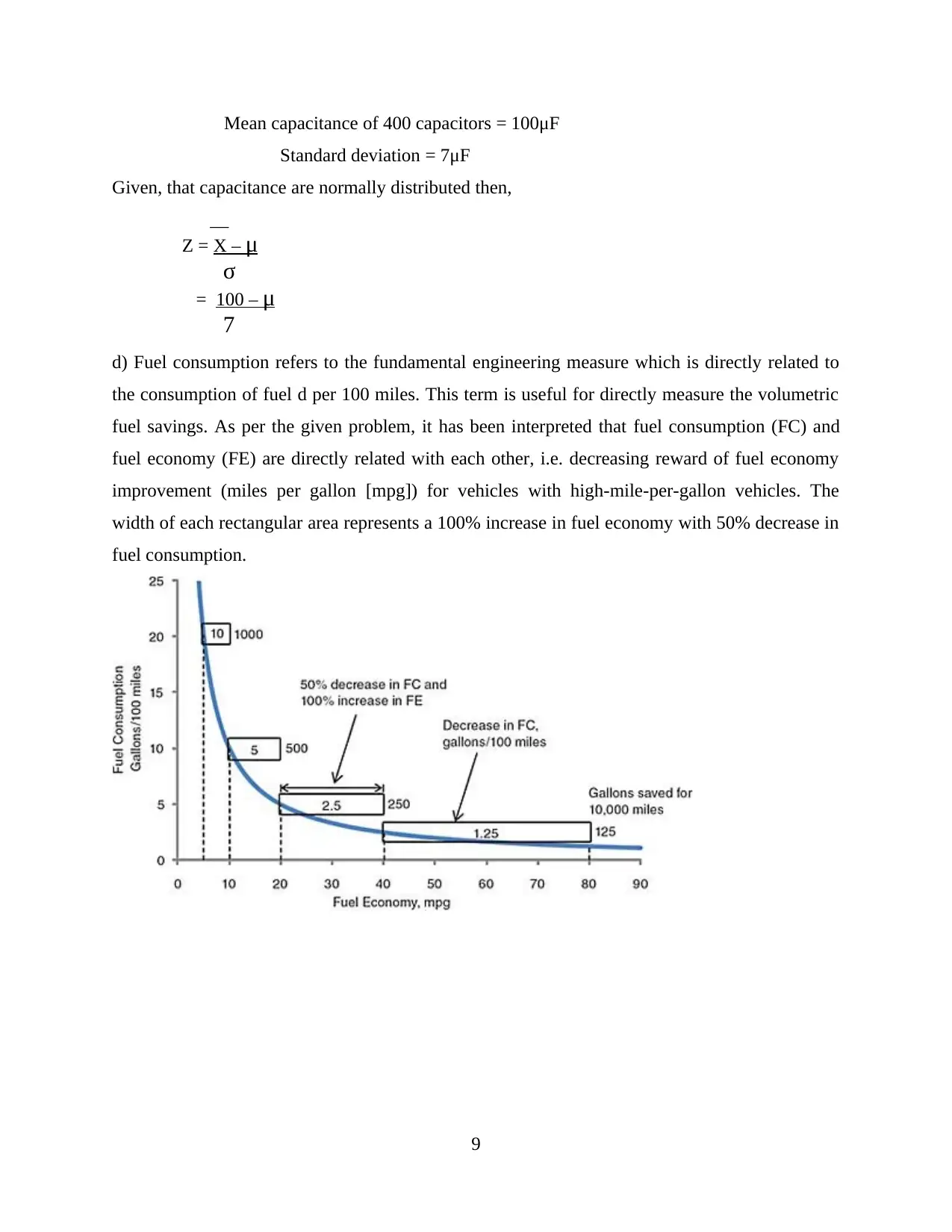
d) Fuel consumption refers to the fundamental engineering measure which is directly related to
the consumption of fuel d per 100 miles. This term is useful for directly measure the volumetric
fuel savings. As per the given problem, it has been interpreted that fuel consumption (FC) and
fuel economy (FE) are directly related with each other, i.e. decreasing reward of fuel economy
improvement (miles per gallon [mpg]) for vehicles with high-mile-per-gallon vehicles. The
width of each rectangular area represents a 100% increase in fuel economy with 50% decrease in
fuel consumption.
9
Standard deviation = 7μF
Given, that capacitance are normally distributed then,
__
Z = X – μ
σ
= 100 – μ
7
d) Fuel consumption refers to the fundamental engineering measure which is directly related to
the consumption of fuel d per 100 miles. This term is useful for directly measure the volumetric
fuel savings. As per the given problem, it has been interpreted that fuel consumption (FC) and
fuel economy (FE) are directly related with each other, i.e. decreasing reward of fuel economy
improvement (miles per gallon [mpg]) for vehicles with high-mile-per-gallon vehicles. The
width of each rectangular area represents a 100% increase in fuel economy with 50% decrease in
fuel consumption.
9

10
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

